第03讲 分式 课件(共44张PPT)-2025年中考数学一轮复习讲练测(全国通用)
文档属性
| 名称 | 第03讲 分式 课件(共44张PPT)-2025年中考数学一轮复习讲练测(全国通用) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 07:25:17 | ||
图片预览





文档简介
(共44张PPT)
第03讲 分 式
第一章 数与式
汇报人:WPS
2大中考命题点+8大题型探究
2大考点精讲+专训
汇报人:WPS
01
考情透视·目标导航
中考考点 考查频率 新课标要求
分式的相关概念
分式的基本性质
分式的化简及求值
★
★★
★★★
了解分式和最简分式的概念.
能利用分式的基本性质进行约分与通分.
能对简单的分式进行加、减、乘、除运算..
【考情分析】本考点主要考查分式的化简和求值,考查形式多样,其中分式的考查以解答题为主,难度一般. 解分式化简、求值问题时,
一要注意整体思想的应用,
二要注意解题技巧(分母为多项式时,先分解因式,进行约分,再计算),
三要注意代入的值要使分式有意义.
02
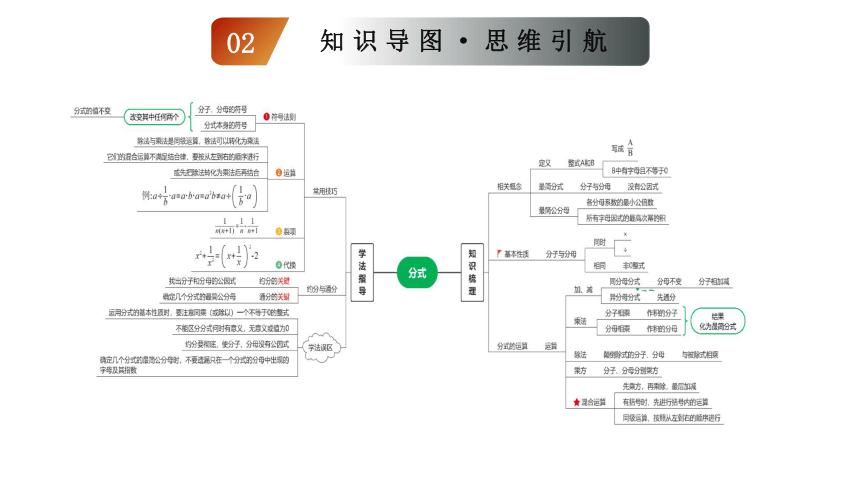
知识导图·思维引航
03
考点突破·考法探究
分式的运算
考点二
分式及其性质
考点一
分式及其性质
1.分式及其性质
分式及其性质
考点一
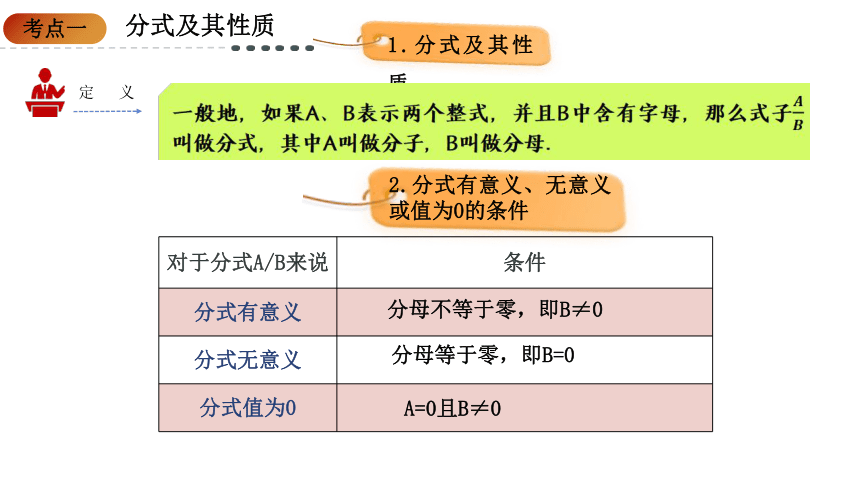
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子叫做分式,其中A叫做分子,B叫做分母.
2.分式有意义、无意义或值为0的条件
对于分式A/B来说 条件
分式有意义
分式无意义
分式值为0
分母不等于零,即B≠0
分母等于零,即B=0
A=0且B≠0
定 义
3.分式的基本性质
分式及其性质
考点一
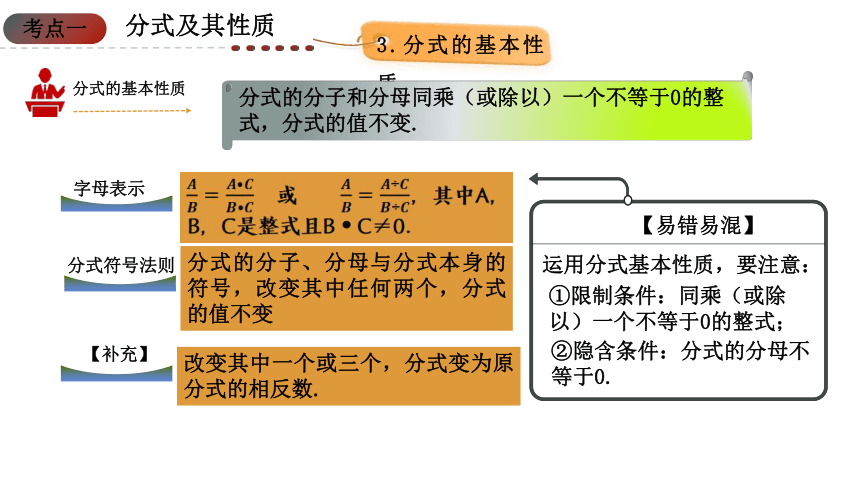
分式的基本性质
分式的分子和分母同乘(或除以)一个不等于0的整式,分式的值不变.
或 ,其中A,B,C是整式且B C≠0.
字母表示
.
【补充】
分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变
改变其中一个或三个,分式变为原分式的相反数.
分式符号法则
【易错易混】
运用分式基本性质,要注意:
①限制条件:同乘(或除以)一个不等于0的整式;
②隐含条件:分式的分母不等于0.
分式及其性质
考点一
4.分式的约分
分式的约分
根据分式的基本性质,约去分子和分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.
最简分式
【补充说明】
分子与分母没有公因式的分式,叫做最简分式.
约分是对分子、分母同时进行的,即分子的整体和分母的整体都除以同一个因式,约分要彻底,使分子、分母没有公因式,而且约分前后分式的值相等.
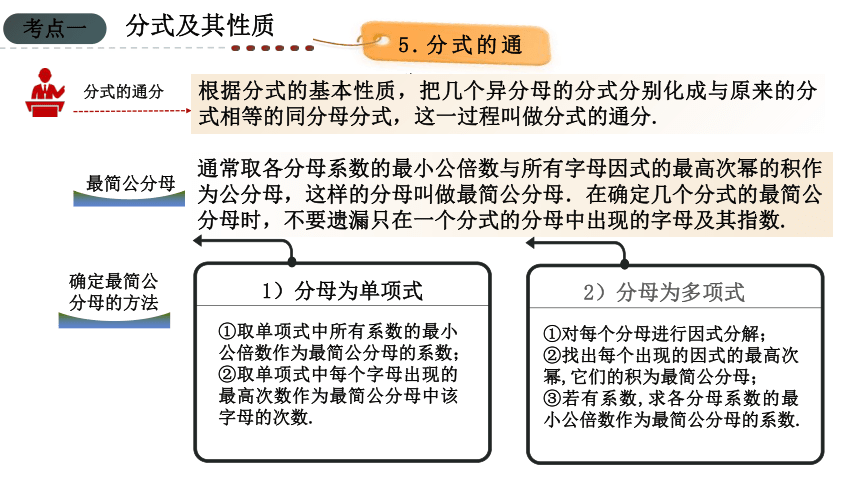
5.分式的通分
分式及其性质
考点一
分式的通分
根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母分式,这一过程叫做分式的通分.
确定最简公分母的方法
最简公分母
通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.在确定几个分式的最简公分母时,不要遗漏只在一个分式的分母中出现的字母及其指数.
1)分母为单项式
2)分母为多项式
①取单项式中所有系数的最小公倍数作为最简公分母的系数;
②取单项式中每个字母出现的最高次数作为最简公分母中该字母的次数.
①对每个分母进行因式分解;
②找出每个出现的因式的最高次幂,它们的积为最简公分母;
③若有系数,求各分母系数的最小公倍数作为最简公分母的系数.
分式及其性质
考点一
针对练习
1.(2022·湖南怀化·中考真题)代数式x,,,x2﹣,,中,属于分式的有( )
A.2个 B.3个 C.4个 D.5个
2.(2023·甘肃兰州·中考真题)计算:( )
A. B. C.5 D.a
3.(2024·四川雅安·中考真题)已知.则( )
A. B.1 C.2 D.3
4.(2024·黑龙江齐齐哈尔·中考真题)在函数中,自变量的取值范围是 .
B
D
C
且
5.(2023·四川南充·中考真题)若分式的值为0,则 .
03
考点突破·考法探究
分式的运算
考点二
分式及其性质
考点一
分式的运算
分式的运算
考点二
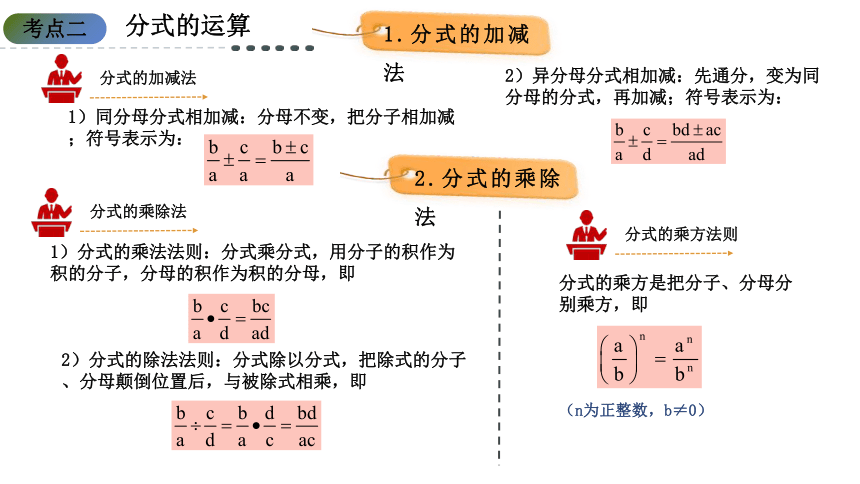
1.分式的加减法
2)分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘,即
分式的加减法
1)同分母分式相加减:分母不变,把分子相加减;符号表示为:
分式的乘除法
1)分式的乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母,即
2.分式的乘除法
分式的乘方法则
分式的乘方是把分子、分母分别乘方,即
(n为正整数,b≠0)
2)异分母分式相加减:先通分,变为同分母的分式,再加减;符号表示为:
分式及其性质
考点一
3.分式的混合运算
运算顺序
分式的混合运算顺序与实数类似,
先乘方,再乘除,最后加减;
即
有括号时,先进行括号内的运算;
同级运算,按照从左到右的顺序进行.
分式及其性质
考点一
针对练习
1.(2024·河北·中考真题)已知A为整式,若计算的结果为,则( )
A.x B.y
C. D.
方法指导
【解析】
由题意得:
∵
∴,
∴
A
分式的加减运算法则
2.(2024·黑龙江大庆·中考真题)先化简,再求值:,其中.
【解析】
当时
原式.
分式的通分、约分运算要先适度进行因式分解
方法指导
针对练习
1.(2024·山东淄博·中考真题)下列运算结果是正数的是( )
A. B. C. D.
A
2.(2024·四川凉山·中考真题)下列各数中:
,负数有( )
A.1个 B.2个 C.3个 D.4个
C
3.(2024·山东日照·中考真题)实数中无理数是( )
A. B.0 C. D.1.732
C
4.(2024·四川雅安·中考真题)将,,,0,,这6个数分别写在6
张同样的卡片上,从中随机抽取1张,卡片上的数为有理数的概率是 .
实数的分类
考点一
04
题型精研·考向洞悉
分式有、无意义的条件
题型01
分式及其性质
命题点一
分式值为0的条件
题型02
方法指导
命题点一 分式及其性
题型01 分式有、无意义的条件
【例1】 (21-22八年级下·广东佛山·阶段练习)当时,分式无意义;当时分式的值为,
则的值是 .
解题的关键:
分式无意义即分母为0
分式的值为零,需同时具备两个条件:
(1)分子为0;(2)分母不为0
∵ =,∴ =0
∴,
∵ ≠0
∴当,时,
,
解:
∵分式无意义,
∴ =0
∴,
命题点一 分式及其性
题型01 分式有、无意义的条件
1.(2023·湖北黄石·中考真题)函数的自变量x的取值范围是( )
A. B. C.且 D.
2.(2024·安徽·中考真题)若代数式有意义,则实数的取值范围是 .
3.(2024·黑龙江大兴安岭地·中考真题)在函数中,自变量x的取值范围是 .
C
分式有意义的条件,
二次根式有意义的条件
分母不能等于
方法指导
命题点一 分式及其性
题型02 分式值为0的条件
【例1】 .(2021·江苏扬州·中考真题)不论x取何值,下列代数式的值不可能为0的是( )
A. B.
C. D.
C
【解析】
A、当x=-1时,x+1=0,故不合题意;
B、当x=±1时,x2-1=0,故不合题意;
C、分子是1,而1≠0,则≠0,故符合题意
D、当x=-1时,,故不合题意;
解题的关键:
分别找到各式为0时的x值,
分式的值为零,需同时具备两个条件:
(1)分子为0;(2)分母不为0
命题点一 分式及其性
题型02 分式值为0的条件
1.(2023·四川凉山·中考真题)分式的值为0,则的值是( )
A.0 B. C.1 D.0或1
2.(2021·四川雅安·中考真题)若分式的值等于0,则x的值为( )
A.﹣1 B.0 C.1 D.±1
3.(2024·山东济南·中考真题)若分式的值为0,则的值是 .
A
A
1
解得,
∵ 1=0,x 1≠0,
∴x= 1,
由题意得:x 1=0,
2x≠0
解得:x=1.
04
题型精研·考向洞悉
分式的运算
题型01
分式的运算
命题点二
判断分式运算的错误步骤
题型02
分式的化简求值
题型03
分式的规律探究
题型05
与分式运算有关的新定义问题
题型06
分式运算的应用
题型04
方法指导
命题点二 分式的运算
题型01 分式的运算
相关公式:
(n为正整数,b≠0)
【例1】 (2024·四川泸州·中考真题)化简:.
解:
通 分
混合运算,有括号先运算括号里面的
除法转化为乘法
约分化简得到结果
方法指导
命题点二 分式的运算
题型01 分式的运算
【例1】 (2023·江西·中考真题)化简.
下面是甲、乙两同学的部分运算过程:
解:原式 …… 解:原式 ……
(1)甲同学解法的依据是________,乙同学解法的依据是________;(填序号)
①等式的基本性质;②分式的基本性质;
③乘法分配律;④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
解题的关键:
甲同学的解法:先根据分式的基本性质把小括号内的分式先通分
乙同学的解法:根据乘法分配律先去括号
②
③
命题点二 分式的运算
题型01 分式的运算
【例1】 (2023·江西·中考真题)化简.
下面是甲、乙两同学的部分运算过程:
解:原式 …… 解:原式 ……
(1)甲同学解法的依据是________,乙同学解法的依据是________;(填序号)
①等式的基本性质;②分式的基本性质;
③乘法分配律;④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
②
③
解:甲同学的解法:
原式
;
乙同学的解法:
原式
.
先去括号计算简便一些
方法指导
1.(2024·广东广州·中考真题)关于的方程有两个不等的实数根.
(1)求的取值范围;
(2)化简:.
解题的关键:
一元二次方程根的判别式和分式的混合运算结合
根据(1)的结论化简绝对值,再计算分式的乘除混合运算
解:
(1)∵关于的方程有两个不等的实数根.
∴,
解得:;
命题点二 分式的运算
题型01 分式的运算
(2)∵,
;
∴
命题点二 分式的运算
题型02 判断分式运算的错误步骤
常见
错误类型
例如:
运算顺序错误,应先算括号里的,再算括号外的.
把分式通分与解方程去分母混淆,要注意分式计算式等式代换,不能去分母.
去括号时没有注意前面的符号.
错误原因
(1)
错在颠倒运算顺序
(2)
错在去分母
(3)
错在符号变化
例如:
例如:
错误原因
错误原因
有分母
无分母
命题点二 分式的运算
题型02 判断分式运算的错误步骤
【例1】 ( (2023·内蒙古通辽·中考真题)
以下是某同学化简分式的部分运算过程:
解:原式…………第一步
…………第二步
…………第三步
……
(1)上面的运算过程中第___________步开始出现了错误;
(2)请你写出完整的解答过程.
一
(2)解:
.
错在颠倒运算顺序
正 确 运 算
命题点二 分式的运算
题型02 判断分式运算的错误步骤
1.(2024·四川乐山·中考真题)先化简,再求值:,其中.小乐同学的计算过程如下:
解:…①
…②
…③
…④
…⑤
当时,原式.
(1)小乐同学的解答过程中,第______步开始出现了错误;
(2)请帮助小乐同学写出正确的解答过程.
③
错在符号变化
解:
当时,原式
正 确 运 算
方法指导
命题点二 分式的运算
题型03 分式的化简求值
(1)
化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤,代入求值的模式一般为“当…时,原式=…”.
(3)
若题干中未明确给出字母的数值,可考虑使用整体代入法.
(2)
若题干中明确给出字母的数值,通常选用直接代入法
方法指导
命题点二 分式的运算
题型03 分式的化简求值
【例1】 (2024·四川广安·中考真题)先化简,再从,,,中选取一个适合的数代入求值.
解:
且
∴当时,原式;
当时,原式.
解题的关键:
先计算括号内分式的加减运算,再计算分式的除法运算
结合分式有意义的条件选合适的值代入
分母不等于0
命题点二 分式的运算
题型03 分式的化简求值
【例2】 (2024·山东淄博·中考真题)化简分式:,并求值(请从小宇和小丽的对话中确定,的值)
解:依题意,,
∵为整数,又,
;
当,时,
原式.
正确理解对话内容得出合理结论
方法指导
1.(2024·山东烟台·中考真题)利用课本上的计算器进行计算,按键顺序如下:
命题点二 分式的运算
题型03 分式的化简求值
若是其显示结果的平方根,先化简:,再求值.
,
∵,
∴的平方根为,
∵,
∴,
又∵为的平方根,
∴,
∴原式.
解:
解题的关键:
正确化简分式
正确求出 的值
(1)解:
命题点二 分式的运算
题型04 分式运算的应用
【例1】 (2023·江苏盐城·中考真题)课堂上,老师提出了下面的问题:
已知,,
试比较与的大小.
小华:整式的大小比较可采用“作差法”.
老师:比较与的大小.
小华:
∵
=
=,
∴.
老师:分式的大小比较能用“作差法”吗?
(1)请用“作差法”完成老师提出的问题.
(2)比较大小:__________.
(填“”“”或“”)
,
,
;
(2)解:
,
.
要正确理解题目出示的材料
命题点二 分式的运算
题型04 分式运算的应用
【例2】 (2024·内蒙古·中考真题)某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍少,其中“丰收1号”小麦种植在边长为的正方形去掉一个边长为的正方形蓄水池后余下的试验田中,“丰收2号”小麦种植在边长为的正方形试验田中.
(1)请分别求出种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量;
(2)哪种小麦的单位面积产量高?高的单位面积产量是低的单位面积产量的多少倍?
方法指导
解题的关键:
正确建立方程
熟练掌握分式除法的应用
丰收1号”小麦
丰收2号”小麦
命题点二 分式的运算
题型04 分式运算的应用
【例2】 (2024·内蒙古·中考真题)某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍少,其中“丰收1号”小麦种植在边长为的正方形去掉一个边长为的正方形蓄水池后余下的试验田中,“丰收2号”小麦种植在边长为的正方形试验田中.
(1)请分别求出种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量;
丰收1号”小麦
丰收2号”小麦
答:种植“丰收1号”小麦试验田的产粮量为,种植“丰收2号”小麦试验田的产粮量为.
(1)解:设种植“丰收1号”小麦试验田的产粮量为,
则种植“丰收2号”小麦试验田的产粮量为,
由题意得:,
解得 ,
∴,
列一元一次方程
命题点二 分式的运算
题型04 分式运算的应用
【例2】 (2024·内蒙古·中考真题)某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍少,其中“丰收1号”小麦种植在边长为的正方形去掉一个边长为的正方形蓄水池后余下的试验田中,“丰收2号”小麦种植在边长为的正方形试验田中.
(2)哪种小麦的单位面积产量高?高的单位面积产量是低的单位面积产量的多少倍?
∴高的单位面积产量是低的单位面积产量的倍.
(2)解:由题意得:
“丰收1号”小麦试验田的面积为,“丰收2号”小麦试验田的面积为,
【分析】
品种 试验田面积 总产量 单位面积产量
丰收1号
丰收2号
,
∴
∵,
∴
,
∴,
∴“丰收2号”小麦试验田的单位面积产量高.
方法指导
命题点二 分式的运算
题型05 分式的规律探究
【例1】 (2023·湖北恩施·一模)对于正数,规定,例如:,,,…利用以上的规律计算: .
解题的关键:
分式化简求值
通过计算发现1
,
解:∵,
∴
,
∴
=
方法指导
按照以上规律.解决下列问题:
写出第个等式 :
;
写出你猜想的第个等式: (用含的等式表示),并证明.
命题点二 分式的运算
题型05 分式的规律探究
【例2】 (2020·安徽·中考真题)观察以下等式:
第1个等式:
第个等式:
第3个等式:
第个等式:
第5个等式:
······
解题的关键:
各式中相同位置数字的变化规律
用代数式表示出变化规律
;
(2)第个等式:
,
证明:
∵左边=
∴左边=右边,
∴等式成立
【解析】
1.(2021·安徽合肥·一模)观察以下等式:
第1个等式: 第2个等式:
第3个等式: 第4个等式:
…
按照以上规律,解决下列问题:
(1)写出第5个等式:
__________________________;
(2)写出你猜想的第n个等式:
,
(用含n的等式表示),并证明.
命题点二 分式的运算
题型05 分式的规律探究
(2)∵第1个等式:
第2个等式:
第3个等式:
第4个等式:
…
∴第n个等式:
∵,
∴等式成立;
【解析】
方法指导
命题点二 分式的运算
题型05 分式的规律探究
2.(2022·浙江舟山·中考真题)观察下面的等式:,,,……
(1)按上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数)
(2)请运用分式的有关知识,推理说明这个结论是正确的.
(1)解:
∵第一个式子,
第二个式子,
第三个式子,
……
∴第(n+1)个式子;
(2)解:∵右边=
∴右边=左边
∴
解题的关键:
通过观察,分析、归纳发现其中各分母的变化规律.
方法指导
命题点二 分式的运算
题型06 与分式运算有关的新定义问题
【例1】(2024·黑龙江哈尔滨·模拟预测)
对于实数a、b,定义运算:
①
②
例如 ①
依此定义方程
的解为 .
解题的关键:
正确理解新定义中计算方式
由题意列出分式方程并熟练解答
解分式方程要检验,注意分母不为0
解:由题意得
解得:
或
检验:
当x=-2时,
x +2=0
不符合题意
∴原方程的解为:
x=3
x=3
方法指导
命题点二 分式的运算
题型06 与分式运算有关的新定义问题
【例2】 (2024·内蒙古乌海·一模)对于任 意两个不相等的正实数a,b,
定义新运算“ ”
规定:
求
中x的取值范围是 .
解题的关键:
根据新定义转化得到分式
定义下的实数运算,二次根式的意义,分式的意义
解:
∴
∴
且
且
命题点二 分式的运算
题型06 与分式运算有关的新定义问题
1.(2024·湖南永州·一模)对于任意两个非零实数a,b
定义新运算“*”如下:
例如:
若
的值为 .
则
1012
解:
(x 、y不为0)
方法指导
解题的关键:
理解定义的新运算
整体代值
感谢观看
汇报人:WPS
第03讲 分 式
第一章 数与式
汇报人:WPS
2大中考命题点+8大题型探究
2大考点精讲+专训
汇报人:WPS
01
考情透视·目标导航
中考考点 考查频率 新课标要求
分式的相关概念
分式的基本性质
分式的化简及求值
★
★★
★★★
了解分式和最简分式的概念.
能利用分式的基本性质进行约分与通分.
能对简单的分式进行加、减、乘、除运算..
【考情分析】本考点主要考查分式的化简和求值,考查形式多样,其中分式的考查以解答题为主,难度一般. 解分式化简、求值问题时,
一要注意整体思想的应用,
二要注意解题技巧(分母为多项式时,先分解因式,进行约分,再计算),
三要注意代入的值要使分式有意义.
02
知识导图·思维引航
03
考点突破·考法探究
分式的运算
考点二
分式及其性质
考点一
分式及其性质
1.分式及其性质
分式及其性质
考点一
一般地,如果A、B表示两个整式,并且B中含有字母,那么式子叫做分式,其中A叫做分子,B叫做分母.
2.分式有意义、无意义或值为0的条件
对于分式A/B来说 条件
分式有意义
分式无意义
分式值为0
分母不等于零,即B≠0
分母等于零,即B=0
A=0且B≠0
定 义
3.分式的基本性质
分式及其性质
考点一
分式的基本性质
分式的分子和分母同乘(或除以)一个不等于0的整式,分式的值不变.
或 ,其中A,B,C是整式且B C≠0.
字母表示
.
【补充】
分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变
改变其中一个或三个,分式变为原分式的相反数.
分式符号法则
【易错易混】
运用分式基本性质,要注意:
①限制条件:同乘(或除以)一个不等于0的整式;
②隐含条件:分式的分母不等于0.
分式及其性质
考点一
4.分式的约分
分式的约分
根据分式的基本性质,约去分子和分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.
最简分式
【补充说明】
分子与分母没有公因式的分式,叫做最简分式.
约分是对分子、分母同时进行的,即分子的整体和分母的整体都除以同一个因式,约分要彻底,使分子、分母没有公因式,而且约分前后分式的值相等.
5.分式的通分
分式及其性质
考点一
分式的通分
根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母分式,这一过程叫做分式的通分.
确定最简公分母的方法
最简公分母
通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.在确定几个分式的最简公分母时,不要遗漏只在一个分式的分母中出现的字母及其指数.
1)分母为单项式
2)分母为多项式
①取单项式中所有系数的最小公倍数作为最简公分母的系数;
②取单项式中每个字母出现的最高次数作为最简公分母中该字母的次数.
①对每个分母进行因式分解;
②找出每个出现的因式的最高次幂,它们的积为最简公分母;
③若有系数,求各分母系数的最小公倍数作为最简公分母的系数.
分式及其性质
考点一
针对练习
1.(2022·湖南怀化·中考真题)代数式x,,,x2﹣,,中,属于分式的有( )
A.2个 B.3个 C.4个 D.5个
2.(2023·甘肃兰州·中考真题)计算:( )
A. B. C.5 D.a
3.(2024·四川雅安·中考真题)已知.则( )
A. B.1 C.2 D.3
4.(2024·黑龙江齐齐哈尔·中考真题)在函数中,自变量的取值范围是 .
B
D
C
且
5.(2023·四川南充·中考真题)若分式的值为0,则 .
03
考点突破·考法探究
分式的运算
考点二
分式及其性质
考点一
分式的运算
分式的运算
考点二
1.分式的加减法
2)分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘,即
分式的加减法
1)同分母分式相加减:分母不变,把分子相加减;符号表示为:
分式的乘除法
1)分式的乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母,即
2.分式的乘除法
分式的乘方法则
分式的乘方是把分子、分母分别乘方,即
(n为正整数,b≠0)
2)异分母分式相加减:先通分,变为同分母的分式,再加减;符号表示为:
分式及其性质
考点一
3.分式的混合运算
运算顺序
分式的混合运算顺序与实数类似,
先乘方,再乘除,最后加减;
即
有括号时,先进行括号内的运算;
同级运算,按照从左到右的顺序进行.
分式及其性质
考点一
针对练习
1.(2024·河北·中考真题)已知A为整式,若计算的结果为,则( )
A.x B.y
C. D.
方法指导
【解析】
由题意得:
∵
∴,
∴
A
分式的加减运算法则
2.(2024·黑龙江大庆·中考真题)先化简,再求值:,其中.
【解析】
当时
原式.
分式的通分、约分运算要先适度进行因式分解
方法指导
针对练习
1.(2024·山东淄博·中考真题)下列运算结果是正数的是( )
A. B. C. D.
A
2.(2024·四川凉山·中考真题)下列各数中:
,负数有( )
A.1个 B.2个 C.3个 D.4个
C
3.(2024·山东日照·中考真题)实数中无理数是( )
A. B.0 C. D.1.732
C
4.(2024·四川雅安·中考真题)将,,,0,,这6个数分别写在6
张同样的卡片上,从中随机抽取1张,卡片上的数为有理数的概率是 .
实数的分类
考点一
04
题型精研·考向洞悉
分式有、无意义的条件
题型01
分式及其性质
命题点一
分式值为0的条件
题型02
方法指导
命题点一 分式及其性
题型01 分式有、无意义的条件
【例1】 (21-22八年级下·广东佛山·阶段练习)当时,分式无意义;当时分式的值为,
则的值是 .
解题的关键:
分式无意义即分母为0
分式的值为零,需同时具备两个条件:
(1)分子为0;(2)分母不为0
∵ =,∴ =0
∴,
∵ ≠0
∴当,时,
,
解:
∵分式无意义,
∴ =0
∴,
命题点一 分式及其性
题型01 分式有、无意义的条件
1.(2023·湖北黄石·中考真题)函数的自变量x的取值范围是( )
A. B. C.且 D.
2.(2024·安徽·中考真题)若代数式有意义,则实数的取值范围是 .
3.(2024·黑龙江大兴安岭地·中考真题)在函数中,自变量x的取值范围是 .
C
分式有意义的条件,
二次根式有意义的条件
分母不能等于
方法指导
命题点一 分式及其性
题型02 分式值为0的条件
【例1】 .(2021·江苏扬州·中考真题)不论x取何值,下列代数式的值不可能为0的是( )
A. B.
C. D.
C
【解析】
A、当x=-1时,x+1=0,故不合题意;
B、当x=±1时,x2-1=0,故不合题意;
C、分子是1,而1≠0,则≠0,故符合题意
D、当x=-1时,,故不合题意;
解题的关键:
分别找到各式为0时的x值,
分式的值为零,需同时具备两个条件:
(1)分子为0;(2)分母不为0
命题点一 分式及其性
题型02 分式值为0的条件
1.(2023·四川凉山·中考真题)分式的值为0,则的值是( )
A.0 B. C.1 D.0或1
2.(2021·四川雅安·中考真题)若分式的值等于0,则x的值为( )
A.﹣1 B.0 C.1 D.±1
3.(2024·山东济南·中考真题)若分式的值为0,则的值是 .
A
A
1
解得,
∵ 1=0,x 1≠0,
∴x= 1,
由题意得:x 1=0,
2x≠0
解得:x=1.
04
题型精研·考向洞悉
分式的运算
题型01
分式的运算
命题点二
判断分式运算的错误步骤
题型02
分式的化简求值
题型03
分式的规律探究
题型05
与分式运算有关的新定义问题
题型06
分式运算的应用
题型04
方法指导
命题点二 分式的运算
题型01 分式的运算
相关公式:
(n为正整数,b≠0)
【例1】 (2024·四川泸州·中考真题)化简:.
解:
通 分
混合运算,有括号先运算括号里面的
除法转化为乘法
约分化简得到结果
方法指导
命题点二 分式的运算
题型01 分式的运算
【例1】 (2023·江西·中考真题)化简.
下面是甲、乙两同学的部分运算过程:
解:原式 …… 解:原式 ……
(1)甲同学解法的依据是________,乙同学解法的依据是________;(填序号)
①等式的基本性质;②分式的基本性质;
③乘法分配律;④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
解题的关键:
甲同学的解法:先根据分式的基本性质把小括号内的分式先通分
乙同学的解法:根据乘法分配律先去括号
②
③
命题点二 分式的运算
题型01 分式的运算
【例1】 (2023·江西·中考真题)化简.
下面是甲、乙两同学的部分运算过程:
解:原式 …… 解:原式 ……
(1)甲同学解法的依据是________,乙同学解法的依据是________;(填序号)
①等式的基本性质;②分式的基本性质;
③乘法分配律;④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
②
③
解:甲同学的解法:
原式
;
乙同学的解法:
原式
.
先去括号计算简便一些
方法指导
1.(2024·广东广州·中考真题)关于的方程有两个不等的实数根.
(1)求的取值范围;
(2)化简:.
解题的关键:
一元二次方程根的判别式和分式的混合运算结合
根据(1)的结论化简绝对值,再计算分式的乘除混合运算
解:
(1)∵关于的方程有两个不等的实数根.
∴,
解得:;
命题点二 分式的运算
题型01 分式的运算
(2)∵,
;
∴
命题点二 分式的运算
题型02 判断分式运算的错误步骤
常见
错误类型
例如:
运算顺序错误,应先算括号里的,再算括号外的.
把分式通分与解方程去分母混淆,要注意分式计算式等式代换,不能去分母.
去括号时没有注意前面的符号.
错误原因
(1)
错在颠倒运算顺序
(2)
错在去分母
(3)
错在符号变化
例如:
例如:
错误原因
错误原因
有分母
无分母
命题点二 分式的运算
题型02 判断分式运算的错误步骤
【例1】 ( (2023·内蒙古通辽·中考真题)
以下是某同学化简分式的部分运算过程:
解:原式…………第一步
…………第二步
…………第三步
……
(1)上面的运算过程中第___________步开始出现了错误;
(2)请你写出完整的解答过程.
一
(2)解:
.
错在颠倒运算顺序
正 确 运 算
命题点二 分式的运算
题型02 判断分式运算的错误步骤
1.(2024·四川乐山·中考真题)先化简,再求值:,其中.小乐同学的计算过程如下:
解:…①
…②
…③
…④
…⑤
当时,原式.
(1)小乐同学的解答过程中,第______步开始出现了错误;
(2)请帮助小乐同学写出正确的解答过程.
③
错在符号变化
解:
当时,原式
正 确 运 算
方法指导
命题点二 分式的运算
题型03 分式的化简求值
(1)
化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤,代入求值的模式一般为“当…时,原式=…”.
(3)
若题干中未明确给出字母的数值,可考虑使用整体代入法.
(2)
若题干中明确给出字母的数值,通常选用直接代入法
方法指导
命题点二 分式的运算
题型03 分式的化简求值
【例1】 (2024·四川广安·中考真题)先化简,再从,,,中选取一个适合的数代入求值.
解:
且
∴当时,原式;
当时,原式.
解题的关键:
先计算括号内分式的加减运算,再计算分式的除法运算
结合分式有意义的条件选合适的值代入
分母不等于0
命题点二 分式的运算
题型03 分式的化简求值
【例2】 (2024·山东淄博·中考真题)化简分式:,并求值(请从小宇和小丽的对话中确定,的值)
解:依题意,,
∵为整数,又,
;
当,时,
原式.
正确理解对话内容得出合理结论
方法指导
1.(2024·山东烟台·中考真题)利用课本上的计算器进行计算,按键顺序如下:
命题点二 分式的运算
题型03 分式的化简求值
若是其显示结果的平方根,先化简:,再求值.
,
∵,
∴的平方根为,
∵,
∴,
又∵为的平方根,
∴,
∴原式.
解:
解题的关键:
正确化简分式
正确求出 的值
(1)解:
命题点二 分式的运算
题型04 分式运算的应用
【例1】 (2023·江苏盐城·中考真题)课堂上,老师提出了下面的问题:
已知,,
试比较与的大小.
小华:整式的大小比较可采用“作差法”.
老师:比较与的大小.
小华:
∵
=
=,
∴.
老师:分式的大小比较能用“作差法”吗?
(1)请用“作差法”完成老师提出的问题.
(2)比较大小:__________.
(填“”“”或“”)
,
,
;
(2)解:
,
.
要正确理解题目出示的材料
命题点二 分式的运算
题型04 分式运算的应用
【例2】 (2024·内蒙古·中考真题)某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍少,其中“丰收1号”小麦种植在边长为的正方形去掉一个边长为的正方形蓄水池后余下的试验田中,“丰收2号”小麦种植在边长为的正方形试验田中.
(1)请分别求出种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量;
(2)哪种小麦的单位面积产量高?高的单位面积产量是低的单位面积产量的多少倍?
方法指导
解题的关键:
正确建立方程
熟练掌握分式除法的应用
丰收1号”小麦
丰收2号”小麦
命题点二 分式的运算
题型04 分式运算的应用
【例2】 (2024·内蒙古·中考真题)某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍少,其中“丰收1号”小麦种植在边长为的正方形去掉一个边长为的正方形蓄水池后余下的试验田中,“丰收2号”小麦种植在边长为的正方形试验田中.
(1)请分别求出种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量;
丰收1号”小麦
丰收2号”小麦
答:种植“丰收1号”小麦试验田的产粮量为,种植“丰收2号”小麦试验田的产粮量为.
(1)解:设种植“丰收1号”小麦试验田的产粮量为,
则种植“丰收2号”小麦试验田的产粮量为,
由题意得:,
解得 ,
∴,
列一元一次方程
命题点二 分式的运算
题型04 分式运算的应用
【例2】 (2024·内蒙古·中考真题)某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍少,其中“丰收1号”小麦种植在边长为的正方形去掉一个边长为的正方形蓄水池后余下的试验田中,“丰收2号”小麦种植在边长为的正方形试验田中.
(2)哪种小麦的单位面积产量高?高的单位面积产量是低的单位面积产量的多少倍?
∴高的单位面积产量是低的单位面积产量的倍.
(2)解:由题意得:
“丰收1号”小麦试验田的面积为,“丰收2号”小麦试验田的面积为,
【分析】
品种 试验田面积 总产量 单位面积产量
丰收1号
丰收2号
,
∴
∵,
∴
,
∴,
∴“丰收2号”小麦试验田的单位面积产量高.
方法指导
命题点二 分式的运算
题型05 分式的规律探究
【例1】 (2023·湖北恩施·一模)对于正数,规定,例如:,,,…利用以上的规律计算: .
解题的关键:
分式化简求值
通过计算发现1
,
解:∵,
∴
,
∴
=
方法指导
按照以上规律.解决下列问题:
写出第个等式 :
;
写出你猜想的第个等式: (用含的等式表示),并证明.
命题点二 分式的运算
题型05 分式的规律探究
【例2】 (2020·安徽·中考真题)观察以下等式:
第1个等式:
第个等式:
第3个等式:
第个等式:
第5个等式:
······
解题的关键:
各式中相同位置数字的变化规律
用代数式表示出变化规律
;
(2)第个等式:
,
证明:
∵左边=
∴左边=右边,
∴等式成立
【解析】
1.(2021·安徽合肥·一模)观察以下等式:
第1个等式: 第2个等式:
第3个等式: 第4个等式:
…
按照以上规律,解决下列问题:
(1)写出第5个等式:
__________________________;
(2)写出你猜想的第n个等式:
,
(用含n的等式表示),并证明.
命题点二 分式的运算
题型05 分式的规律探究
(2)∵第1个等式:
第2个等式:
第3个等式:
第4个等式:
…
∴第n个等式:
∵,
∴等式成立;
【解析】
方法指导
命题点二 分式的运算
题型05 分式的规律探究
2.(2022·浙江舟山·中考真题)观察下面的等式:,,,……
(1)按上面的规律归纳出一个一般的结论(用含n的等式表示,n为正整数)
(2)请运用分式的有关知识,推理说明这个结论是正确的.
(1)解:
∵第一个式子,
第二个式子,
第三个式子,
……
∴第(n+1)个式子;
(2)解:∵右边=
∴右边=左边
∴
解题的关键:
通过观察,分析、归纳发现其中各分母的变化规律.
方法指导
命题点二 分式的运算
题型06 与分式运算有关的新定义问题
【例1】(2024·黑龙江哈尔滨·模拟预测)
对于实数a、b,定义运算:
①
②
例如 ①
依此定义方程
的解为 .
解题的关键:
正确理解新定义中计算方式
由题意列出分式方程并熟练解答
解分式方程要检验,注意分母不为0
解:由题意得
解得:
或
检验:
当x=-2时,
x +2=0
不符合题意
∴原方程的解为:
x=3
x=3
方法指导
命题点二 分式的运算
题型06 与分式运算有关的新定义问题
【例2】 (2024·内蒙古乌海·一模)对于任 意两个不相等的正实数a,b,
定义新运算“ ”
规定:
求
中x的取值范围是 .
解题的关键:
根据新定义转化得到分式
定义下的实数运算,二次根式的意义,分式的意义
解:
∴
∴
且
且
命题点二 分式的运算
题型06 与分式运算有关的新定义问题
1.(2024·湖南永州·一模)对于任意两个非零实数a,b
定义新运算“*”如下:
例如:
若
的值为 .
则
1012
解:
(x 、y不为0)
方法指导
解题的关键:
理解定义的新运算
整体代值
感谢观看
汇报人:WPS
同课章节目录
