专题04实数(考点串讲,3大考点 6大题型突破 4大技巧突破 4大易错剖析)课件(共45张PPT)-八年级数学上学期期末考点大串讲(苏科版)
文档属性
| 名称 | 专题04实数(考点串讲,3大考点 6大题型突破 4大技巧突破 4大易错剖析)课件(共45张PPT)-八年级数学上学期期末考点大串讲(苏科版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
八年级数学上学期·期末复习大串讲
专题04 实数
苏科版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理
6大题型典例剖析+四大技巧
4大易错易混经典例题
精选5道期末真题对应考点练
目录
考点一 实数的相关概念
不
平方根
正数
0
负数
算术平方根
立方根
正数
0
负数
考点一 实数的相关概念
【热考】
0
0
0
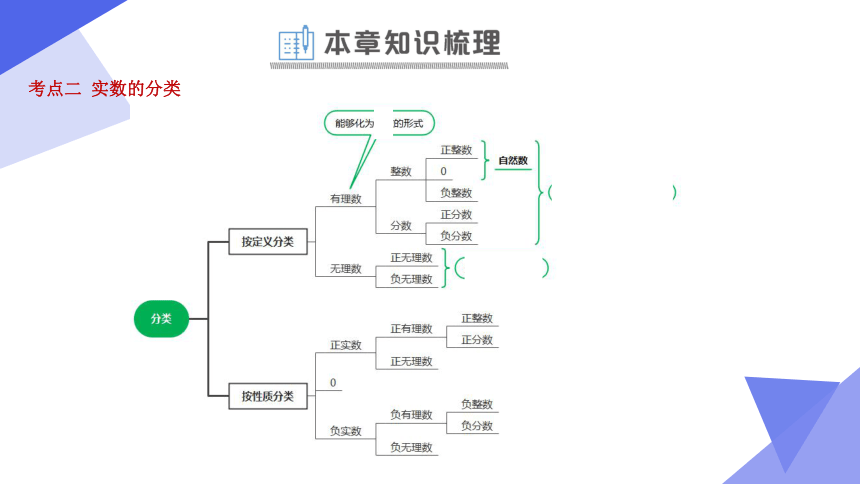
考点二 实数的分类
考点三 实数的运算
相加
减去
相反数
相乘
正数
负数
0
相除
0
乘方
考点一 实数的相关概念
1. 9的平方根是( ).
A. B.3 C. D.
2. (2022上·北京昌平·八年级统考期中)已知一个正数m的两个平方根为和,求a和m的值.
3. (2020·广东·统考中考真题)若,则
C
【解答】解:由题意得,,
∴,∴,∴.
【详解】∵
∴,,
∴ ,
故答案为:1.
考点一 实数的相关概念
4.(2023下·四川广元·七年级统考阶段练习)解方程:
(1)
(2).
【详解】(1)(1)
移项得:,
系数化为1得:
解得:;
(2)(2)
方程两边同时除以8,得:,
∴,
解得:.
5(2023上·江苏常州·八年级统考期末)已知,求x的值.
【详解】解:,
.
,.
考点一 实数的相关概念
6.(2023下·山东菏泽·八年级统考期中)一个数x的立方根是3,则的算术平方根是 .
【详解】解:∵,∴,
∴,
∴.
故答案为:6.
7(2023上·河北保定·八年级定兴二中校考期中)若,,则的值为( )
A.2或 B.或1 C.6或0 D.2或
【详解】解:∵,∴,解得:或,
∵,∴,
当,时,,
当,时,,
综上分析可知,的值为6或0.选:C.
考点二 实数的分类
1.(2023上·湖南张家界·八年级统考期末)在实数,,0,,,3.1415,中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
B
2.(2022上·河北石家庄·八年级统考期末)把下列各数写入相应的集合内:.
(1)有理数集合:{ …}
(2)正实数集合:{ …}
(3)无理数集合:{ …}
(4)负实数集合:{ …}
【详解】(1)解:,,,
有理数集合为:.
(2)解:正实数集合为:.
(3)解:无理数集合为:.
(4)解:负实数集合:.
考点三 实数的运算
1.计算:
(1);
(2).
【详解】(1)解:;
(2).
2.有一个数值转换器,原理如下,当输入的x为81时,输出的y是( )
A. B.9 C.3 D.
B
考点三 实数的运算
3.如图,将长方形分成四个区域,其中A,B两正方形区域的面积分别是3和9.
(1)A,B两正方形的边长各是多少?
(2)求图中阴影部分的面积(结果保留两位小数.参考数据:).
【详解】(1)解:∵正方形A和正方形B的面积分别为3和9,
∴正方形A和正方形B的边长各是;
(2)解:由题意得:.
题型剖析
题型一:非负性的应用
1.已知直角三角形的两直角边、满足,则斜边上的中线长为 .
【详解】解:∵,,
∴
,,
,,
由勾股定理得,斜边,
所以,斜边中线长.
故答案为:.
题型剖析
题型一:非负性的应用
2.(24-25八年级上·江苏宿迁·期中)已知a,b,c满足,则的平方根是 .
【详解】解:,,,,
,
,
,
的平方根是.
故答案为:.
题型剖析
题型二:平方根与立方根综合
1. (2022上·吉林长春·八年级吉林大学附属中学校考期末)若是的算术平方根,是的立方根,则的值为 .
【详解】解: 是即4的算术平方根,,
是的立方根,,,
题型剖析
题型二:平方根与立方根综合
2.(23-24八年级上·江苏盐城·期中)已知的立方根是3,的算术平方根是5,求的平方根.
【详解】解:的立方根是3,
,
,
的算术平方根是5,
,
,
,
的平方根是,
的平方根是.
题型剖析
题型二:平方根与立方根综合
3.(2021上·湖南长沙·七年级长沙市开福区青竹湖湘一外国语学校校考期末)已知:的立方根是,的算术平方根3,是的整数部分.
(1)求的值;
(2)求的平方根.
【详解】解:(1)由题得.
.又,
. .
.
(2)当时,.
∴其平方根为.
题型剖析
题型三:无理数的估算
1.(2023下·重庆梁平·八年级统考期末)估计的值应在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
2.(2023下·山东烟台·八年级统考期末)整数,满足,则 .
【详解】∵,即,∴.故选:D.
【详解】解:,,而整数,满足,
或,故答案为:或.
题型剖析
题型三:无理数的估算
3.(2022·福建·模拟预测)如图,数轴上的点P表示下列四个无理数中的一个,这个无理数是( )
A. B. C. D.π
4.(23-24八年级上·江苏苏州·期中)在如图所示的数轴上表示的点在( )
A.点A和点B之间 B.点B和点C之间
C.点C和点D之间 D.点D和点E之间
B
C
题型剖析
题型四:实数与数轴
1.实数a、b在数轴上所对应的点如图所示,则|﹣b|+|a+|+的值 .
【详解】解:由数轴可得:a<﹣,0<b<,
故|﹣b|+|a+|+
=﹣b﹣(a+)﹣a
=﹣b﹣a﹣﹣a
=﹣2a﹣b.
故答案为:﹣2a﹣b.
题型剖析
题型四:实数与数轴
2. 已知在数轴上的对应点如图所示,化简:
【详解】解:根据数轴上点的位置得:,,
∴,,
∴
.
题型剖析
题型四:实数与数轴
3.(21-22八年级下·江苏南通·阶段练习)实数a、b、c在数轴上的位置如图所示,化简.
【详解】由数轴可得,
∴,,,,
∴
.
题型剖析
题型五:新定义问题
1.现定义一个新运算“※”,规定对于任意实数x,y,都有,则的值为 .
【详解】.故答案为:8.
2.(24-25七年级上·江苏无锡·期中)对于两个有理数a、b,我们对运算“”作出如下定义:
(1)计算: ;
(2)若,求的值.
【详解】(1)解:∵,
∴,
故答案为:22;
(2)解:∵,
∴,
∴
,
,
,
.
题型剖析
题型五:新定义问题
3.(24-25九年级上·湖北省直辖县级单位·阶段练习)对于任意的两个实数a,b,定义运算※如下:若,则 .
【详解】解:当时,∵,∴,∴,解得或;
当时,∵,∴,∴;
综上所述,或,
4.(23-24八年级上·江苏苏州·期中)定义:不超过实数的最大整数成为的整数部分,记作.例如,.按此规定, .
【详解】解:∵不超过实数的最大整数成为的整数部分,记作,
,
∴,
∴,
题型剖析
题型六:规律探究问题
1.若,,,,则的值为( )
A. B. C. D.
【详解】解:,,,,
.故选C
题型剖析
题型六:规律探究问题
2.(22-23七年级下·四川广元·期中)已知按照一定规律排成的一列实数:,,,,,,,,,,…,则按此规律可推得这一列数中的第个数是 .
3.(21-22八年级下·山东滨州·期末)观察下列各式:
,,,……
请利用你所发现的规律,计算,其结果为 .
【详解】由题意得:
,
技巧突破
技巧一:实数的比较大小
解题方法:实数比较大小的常用方法
1)两个负数比较大小,绝对值大的数反而小;
2)将实数在数轴上表示出来,左边的数小于右边的数;
3)作差或作商法:作差后与0进行比较,作商后与1进行比较;
4)估算法:常见≈1.414,≈1.732,≈2.236;
5)乘方法:符号相同的两个根式,利用乘方法来比较大小.
技巧突破
技巧一:实数的比较大小
1.(2021上·山东菏泽·八年级练习)若,,,则下列关系正确的是( ).
A. B.
C. D.
D
2.(23-24八年级上·北京昌平·期中)阅读理解,并回答问题.
阅读材料1:∵,∴,即.∴的整数部分为2,小数部分为.
阅读材料2:对于任意实数a和b比较大小,有如下规律:若,则;若,则;若,则.我们把这种比较两个数大小的方法称为作差法.
例如:比较与的大小时,可以计算,得,
∵,∴.∴.
(1)请表示出的整数部分和小数部分;
(2)试判断与的大小,并说明理由.
【详解】(1)解:∵,∴,
则的整数部分为,小数部分为;
(2)解:,理由如下,
∵,
∴.
技巧突破
技巧二:算术平方根/立方根有关的规律探究
技巧突破
技巧二:算术平方根/立方根有关的规律探究
… …
… …
1.(23-24八年级上·河北沧州·期中)探索与应用:先观察表格,再回答问题.
(1)表格中_____________;_____________;
(2)从表格中探究a与变化的规律:__________________________;
(3)利用规律解决问题:
①已知,则_____________;
②已知,若,则_____________;
(4)拓展:已知,若,则_____________.
技巧突破
技巧二:算术平方根/立方根有关的规律探究
2.(2023下·河北廊坊·七年级校考期中)已知,则的值是( )
A. B. C. D.
D
【详解】∵,
∴
故选:D.
【点睛】本题考查了被开方数的变化与立方根的值的变化之间的变化规律.当被开方数的小数点每向右(或向左)移动3位,它的立方根的小数点就相应的向右(或向左)移动1位.
技巧突破
技巧三:求无理数整数部分与小数部分
技巧突破
技巧三:求无理数整数部分与小数部分
1. 若的整数部分为,小数部分为,则 , .
2. 已知a,b分别是的整数部分和小数部分,则2a﹣b的值为 .
【详解】解:,
,则.
【详解】∵9<13<16,∴3<<4,
∴a=3,b=﹣3,∴2a﹣b=2×3﹣(﹣3)=6﹣+3=.
故答案为.
技巧突破
技巧三:求无理数整数部分与小数部分
3.(23-24八年级上·江苏泰州·期末)【阅读材料】∵,即,∴,∴的整数部分为,∴的小数部分为.
【解决问题】
(1)填空:的小数部分是 ;
(2)已知、分别是的整数部分、小数部分,求代数式的值.
【详解】(1)∵,
∴的整数部分是,
∴的小数部分是,
故答案为;
(2)∵、分别是的整数部分、小数部分,
∴,,
∴
,
,
,
.
技巧突破
技巧四:程序下的实数运算
技巧突破
技巧四:程序下的实数运算
1.(23-24七年级下·广东阳江·期中)如图是一个数值转换器,请根据其原理解决问题:当x为12时,求y的值,并写出详细过程.
【详解】解:把代入数值转换器,第一次计算可得,为有理数,进行第二次计算,
把代入数值转换器,第二次计算可得,为无理数,
则输出.
技巧突破
技巧四:程序下的实数运算
2.(23-24七年级下·江苏南通·期中)如图是一个数值转换器示意图:
(1)当输入的x为36时,输出的y的值是_______;
(2)若输入x值后,始终输不出y的值,则满足题意的x值是_______;
(3)若输出的,则x的最小整数值是_______.
0和1
5
易混易错
类型一:忽略隐含运算而出错
1的平方根是( )
A. B. C. D.
D
类型二:求形如“ ”中x的值时遗漏
2则x=
易混易错
类型三:对无理数的概念理解不透彻
3.(23-24八年级上·宁夏银川·期中)把下列各数分别填入所属的集合中:
①;②;③;④0;⑤;⑥;⑦;⑧;⑨
无理数:{_____________________________};
;;,
类型四:求精确度时出错
4.按括号内的要求,用四舍五入法对下列各数取近似数,并将结果写在后面的横线上.
()(精确到); ;
()(精确到十分位); ;
()(精确到); ;
()(精确到个位); ;
()(精确到); ;
()(精确到千分位). .
答案为:;;;;;
押题预测
1.(23-24八年级上·江苏无锡·期末)计算与化简:
(1) ;
(2).
【详解】(1)解:原式 ;
(2)解:原式.
押题预测
3.(22-23八年级·陕西安康·期末)一个正数的两个不同的平方根分别是和.
(1)求和的值.
(2)求的平方根.
【详解】(1)解:∵一个正数的两个不同的平方根分别是和,
∴,解得,
∴;
(2)解:将代入中,
得,
∵的平方根为,
∴的平方根为.
押题预测
3.(22-23八年级·福建莆田·期末)已知的算术平方根是3,的平方根是,c是的整数部分,求的平方根.
【详解】解:由题意得:
,.
,
.
.
.
的平方根是.
押题预测
4.(23-24八年级上·江苏连云港·期末)如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)求的值;
(2)在数轴上还有C、D两点分别表示实数c和d,且有与互为相反数,求:的平方根.
【详解】(1)解:∵,
∴,
∴,
∴
;
(2)∵与互为相反数,
∴,
∵,,
∴,,
∴,,
∴,
∴的平方根是.
押题预测
5.(24-25八年级上·河南期末)已知甲正方体纸盒的底面积为,乙正方体纸盒的体积比甲正方体纸盒的体积大,丙正方体纸盒的体积是乙正方体纸盒体积的.
(1)求乙正方体纸盒的体积.
(2)求丙正方体纸盒的棱长.
【详解】(1)解:∵甲正方体纸盒的底面积为,
∴甲正方体纸盒的边长为,
∴甲正方体纸盒的体积为:,
∵乙正方体纸盒的体积比甲正方体纸盒的体积大,
∴乙正方体纸盒的体积为.
(2)解:∵丙正方体纸盒的体积是乙正方体纸盒体积的,
∴丙正方体的体积为:,
∴丙正方体纸盒的棱长为.
八年级数学上学期·期末复习大串讲
专题04 实数
苏科版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理
6大题型典例剖析+四大技巧
4大易错易混经典例题
精选5道期末真题对应考点练
目录
考点一 实数的相关概念
不
平方根
正数
0
负数
算术平方根
立方根
正数
0
负数
考点一 实数的相关概念
【热考】
0
0
0
考点二 实数的分类
考点三 实数的运算
相加
减去
相反数
相乘
正数
负数
0
相除
0
乘方
考点一 实数的相关概念
1. 9的平方根是( ).
A. B.3 C. D.
2. (2022上·北京昌平·八年级统考期中)已知一个正数m的两个平方根为和,求a和m的值.
3. (2020·广东·统考中考真题)若,则
C
【解答】解:由题意得,,
∴,∴,∴.
【详解】∵
∴,,
∴ ,
故答案为:1.
考点一 实数的相关概念
4.(2023下·四川广元·七年级统考阶段练习)解方程:
(1)
(2).
【详解】(1)(1)
移项得:,
系数化为1得:
解得:;
(2)(2)
方程两边同时除以8,得:,
∴,
解得:.
5(2023上·江苏常州·八年级统考期末)已知,求x的值.
【详解】解:,
.
,.
考点一 实数的相关概念
6.(2023下·山东菏泽·八年级统考期中)一个数x的立方根是3,则的算术平方根是 .
【详解】解:∵,∴,
∴,
∴.
故答案为:6.
7(2023上·河北保定·八年级定兴二中校考期中)若,,则的值为( )
A.2或 B.或1 C.6或0 D.2或
【详解】解:∵,∴,解得:或,
∵,∴,
当,时,,
当,时,,
综上分析可知,的值为6或0.选:C.
考点二 实数的分类
1.(2023上·湖南张家界·八年级统考期末)在实数,,0,,,3.1415,中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
B
2.(2022上·河北石家庄·八年级统考期末)把下列各数写入相应的集合内:.
(1)有理数集合:{ …}
(2)正实数集合:{ …}
(3)无理数集合:{ …}
(4)负实数集合:{ …}
【详解】(1)解:,,,
有理数集合为:.
(2)解:正实数集合为:.
(3)解:无理数集合为:.
(4)解:负实数集合:.
考点三 实数的运算
1.计算:
(1);
(2).
【详解】(1)解:;
(2).
2.有一个数值转换器,原理如下,当输入的x为81时,输出的y是( )
A. B.9 C.3 D.
B
考点三 实数的运算
3.如图,将长方形分成四个区域,其中A,B两正方形区域的面积分别是3和9.
(1)A,B两正方形的边长各是多少?
(2)求图中阴影部分的面积(结果保留两位小数.参考数据:).
【详解】(1)解:∵正方形A和正方形B的面积分别为3和9,
∴正方形A和正方形B的边长各是;
(2)解:由题意得:.
题型剖析
题型一:非负性的应用
1.已知直角三角形的两直角边、满足,则斜边上的中线长为 .
【详解】解:∵,,
∴
,,
,,
由勾股定理得,斜边,
所以,斜边中线长.
故答案为:.
题型剖析
题型一:非负性的应用
2.(24-25八年级上·江苏宿迁·期中)已知a,b,c满足,则的平方根是 .
【详解】解:,,,,
,
,
,
的平方根是.
故答案为:.
题型剖析
题型二:平方根与立方根综合
1. (2022上·吉林长春·八年级吉林大学附属中学校考期末)若是的算术平方根,是的立方根,则的值为 .
【详解】解: 是即4的算术平方根,,
是的立方根,,,
题型剖析
题型二:平方根与立方根综合
2.(23-24八年级上·江苏盐城·期中)已知的立方根是3,的算术平方根是5,求的平方根.
【详解】解:的立方根是3,
,
,
的算术平方根是5,
,
,
,
的平方根是,
的平方根是.
题型剖析
题型二:平方根与立方根综合
3.(2021上·湖南长沙·七年级长沙市开福区青竹湖湘一外国语学校校考期末)已知:的立方根是,的算术平方根3,是的整数部分.
(1)求的值;
(2)求的平方根.
【详解】解:(1)由题得.
.又,
. .
.
(2)当时,.
∴其平方根为.
题型剖析
题型三:无理数的估算
1.(2023下·重庆梁平·八年级统考期末)估计的值应在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间
2.(2023下·山东烟台·八年级统考期末)整数,满足,则 .
【详解】∵,即,∴.故选:D.
【详解】解:,,而整数,满足,
或,故答案为:或.
题型剖析
题型三:无理数的估算
3.(2022·福建·模拟预测)如图,数轴上的点P表示下列四个无理数中的一个,这个无理数是( )
A. B. C. D.π
4.(23-24八年级上·江苏苏州·期中)在如图所示的数轴上表示的点在( )
A.点A和点B之间 B.点B和点C之间
C.点C和点D之间 D.点D和点E之间
B
C
题型剖析
题型四:实数与数轴
1.实数a、b在数轴上所对应的点如图所示,则|﹣b|+|a+|+的值 .
【详解】解:由数轴可得:a<﹣,0<b<,
故|﹣b|+|a+|+
=﹣b﹣(a+)﹣a
=﹣b﹣a﹣﹣a
=﹣2a﹣b.
故答案为:﹣2a﹣b.
题型剖析
题型四:实数与数轴
2. 已知在数轴上的对应点如图所示,化简:
【详解】解:根据数轴上点的位置得:,,
∴,,
∴
.
题型剖析
题型四:实数与数轴
3.(21-22八年级下·江苏南通·阶段练习)实数a、b、c在数轴上的位置如图所示,化简.
【详解】由数轴可得,
∴,,,,
∴
.
题型剖析
题型五:新定义问题
1.现定义一个新运算“※”,规定对于任意实数x,y,都有,则的值为 .
【详解】.故答案为:8.
2.(24-25七年级上·江苏无锡·期中)对于两个有理数a、b,我们对运算“”作出如下定义:
(1)计算: ;
(2)若,求的值.
【详解】(1)解:∵,
∴,
故答案为:22;
(2)解:∵,
∴,
∴
,
,
,
.
题型剖析
题型五:新定义问题
3.(24-25九年级上·湖北省直辖县级单位·阶段练习)对于任意的两个实数a,b,定义运算※如下:若,则 .
【详解】解:当时,∵,∴,∴,解得或;
当时,∵,∴,∴;
综上所述,或,
4.(23-24八年级上·江苏苏州·期中)定义:不超过实数的最大整数成为的整数部分,记作.例如,.按此规定, .
【详解】解:∵不超过实数的最大整数成为的整数部分,记作,
,
∴,
∴,
题型剖析
题型六:规律探究问题
1.若,,,,则的值为( )
A. B. C. D.
【详解】解:,,,,
.故选C
题型剖析
题型六:规律探究问题
2.(22-23七年级下·四川广元·期中)已知按照一定规律排成的一列实数:,,,,,,,,,,…,则按此规律可推得这一列数中的第个数是 .
3.(21-22八年级下·山东滨州·期末)观察下列各式:
,,,……
请利用你所发现的规律,计算,其结果为 .
【详解】由题意得:
,
技巧突破
技巧一:实数的比较大小
解题方法:实数比较大小的常用方法
1)两个负数比较大小,绝对值大的数反而小;
2)将实数在数轴上表示出来,左边的数小于右边的数;
3)作差或作商法:作差后与0进行比较,作商后与1进行比较;
4)估算法:常见≈1.414,≈1.732,≈2.236;
5)乘方法:符号相同的两个根式,利用乘方法来比较大小.
技巧突破
技巧一:实数的比较大小
1.(2021上·山东菏泽·八年级练习)若,,,则下列关系正确的是( ).
A. B.
C. D.
D
2.(23-24八年级上·北京昌平·期中)阅读理解,并回答问题.
阅读材料1:∵,∴,即.∴的整数部分为2,小数部分为.
阅读材料2:对于任意实数a和b比较大小,有如下规律:若,则;若,则;若,则.我们把这种比较两个数大小的方法称为作差法.
例如:比较与的大小时,可以计算,得,
∵,∴.∴.
(1)请表示出的整数部分和小数部分;
(2)试判断与的大小,并说明理由.
【详解】(1)解:∵,∴,
则的整数部分为,小数部分为;
(2)解:,理由如下,
∵,
∴.
技巧突破
技巧二:算术平方根/立方根有关的规律探究
技巧突破
技巧二:算术平方根/立方根有关的规律探究
… …
… …
1.(23-24八年级上·河北沧州·期中)探索与应用:先观察表格,再回答问题.
(1)表格中_____________;_____________;
(2)从表格中探究a与变化的规律:__________________________;
(3)利用规律解决问题:
①已知,则_____________;
②已知,若,则_____________;
(4)拓展:已知,若,则_____________.
技巧突破
技巧二:算术平方根/立方根有关的规律探究
2.(2023下·河北廊坊·七年级校考期中)已知,则的值是( )
A. B. C. D.
D
【详解】∵,
∴
故选:D.
【点睛】本题考查了被开方数的变化与立方根的值的变化之间的变化规律.当被开方数的小数点每向右(或向左)移动3位,它的立方根的小数点就相应的向右(或向左)移动1位.
技巧突破
技巧三:求无理数整数部分与小数部分
技巧突破
技巧三:求无理数整数部分与小数部分
1. 若的整数部分为,小数部分为,则 , .
2. 已知a,b分别是的整数部分和小数部分,则2a﹣b的值为 .
【详解】解:,
,则.
【详解】∵9<13<16,∴3<<4,
∴a=3,b=﹣3,∴2a﹣b=2×3﹣(﹣3)=6﹣+3=.
故答案为.
技巧突破
技巧三:求无理数整数部分与小数部分
3.(23-24八年级上·江苏泰州·期末)【阅读材料】∵,即,∴,∴的整数部分为,∴的小数部分为.
【解决问题】
(1)填空:的小数部分是 ;
(2)已知、分别是的整数部分、小数部分,求代数式的值.
【详解】(1)∵,
∴的整数部分是,
∴的小数部分是,
故答案为;
(2)∵、分别是的整数部分、小数部分,
∴,,
∴
,
,
,
.
技巧突破
技巧四:程序下的实数运算
技巧突破
技巧四:程序下的实数运算
1.(23-24七年级下·广东阳江·期中)如图是一个数值转换器,请根据其原理解决问题:当x为12时,求y的值,并写出详细过程.
【详解】解:把代入数值转换器,第一次计算可得,为有理数,进行第二次计算,
把代入数值转换器,第二次计算可得,为无理数,
则输出.
技巧突破
技巧四:程序下的实数运算
2.(23-24七年级下·江苏南通·期中)如图是一个数值转换器示意图:
(1)当输入的x为36时,输出的y的值是_______;
(2)若输入x值后,始终输不出y的值,则满足题意的x值是_______;
(3)若输出的,则x的最小整数值是_______.
0和1
5
易混易错
类型一:忽略隐含运算而出错
1的平方根是( )
A. B. C. D.
D
类型二:求形如“ ”中x的值时遗漏
2则x=
易混易错
类型三:对无理数的概念理解不透彻
3.(23-24八年级上·宁夏银川·期中)把下列各数分别填入所属的集合中:
①;②;③;④0;⑤;⑥;⑦;⑧;⑨
无理数:{_____________________________};
;;,
类型四:求精确度时出错
4.按括号内的要求,用四舍五入法对下列各数取近似数,并将结果写在后面的横线上.
()(精确到); ;
()(精确到十分位); ;
()(精确到); ;
()(精确到个位); ;
()(精确到); ;
()(精确到千分位). .
答案为:;;;;;
押题预测
1.(23-24八年级上·江苏无锡·期末)计算与化简:
(1) ;
(2).
【详解】(1)解:原式 ;
(2)解:原式.
押题预测
3.(22-23八年级·陕西安康·期末)一个正数的两个不同的平方根分别是和.
(1)求和的值.
(2)求的平方根.
【详解】(1)解:∵一个正数的两个不同的平方根分别是和,
∴,解得,
∴;
(2)解:将代入中,
得,
∵的平方根为,
∴的平方根为.
押题预测
3.(22-23八年级·福建莆田·期末)已知的算术平方根是3,的平方根是,c是的整数部分,求的平方根.
【详解】解:由题意得:
,.
,
.
.
.
的平方根是.
押题预测
4.(23-24八年级上·江苏连云港·期末)如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)求的值;
(2)在数轴上还有C、D两点分别表示实数c和d,且有与互为相反数,求:的平方根.
【详解】(1)解:∵,
∴,
∴,
∴
;
(2)∵与互为相反数,
∴,
∵,,
∴,,
∴,,
∴,
∴的平方根是.
押题预测
5.(24-25八年级上·河南期末)已知甲正方体纸盒的底面积为,乙正方体纸盒的体积比甲正方体纸盒的体积大,丙正方体纸盒的体积是乙正方体纸盒体积的.
(1)求乙正方体纸盒的体积.
(2)求丙正方体纸盒的棱长.
【详解】(1)解:∵甲正方体纸盒的底面积为,
∴甲正方体纸盒的边长为,
∴甲正方体纸盒的体积为:,
∵乙正方体纸盒的体积比甲正方体纸盒的体积大,
∴乙正方体纸盒的体积为.
(2)解:∵丙正方体纸盒的体积是乙正方体纸盒体积的,
∴丙正方体的体积为:,
∴丙正方体纸盒的棱长为.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
