专题05 平面直角坐标系(考点串讲,5大考点 6大题型突破 3大技巧突破 3大易错剖析 4道期末预测题)课件(共38张PPT)-八年级数学上学期期末考点大串讲(苏科版)
文档属性
| 名称 | 专题05 平面直角坐标系(考点串讲,5大考点 6大题型突破 3大技巧突破 3大易错剖析 4道期末预测题)课件(共38张PPT)-八年级数学上学期期末考点大串讲(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 07:31:43 | ||
图片预览







文档简介
(共38张PPT)
八年级数学上学期·期末复习大串讲
专题05 平面直角坐标系
苏科版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
5大常考点:知识梳理
6大题型典例剖析+3大技巧
3大易错易混经典例题
精选4道期末真题对应考点练
目录
考点一 平面直角坐标系的相关概念
考点二 象限内点的坐标特征
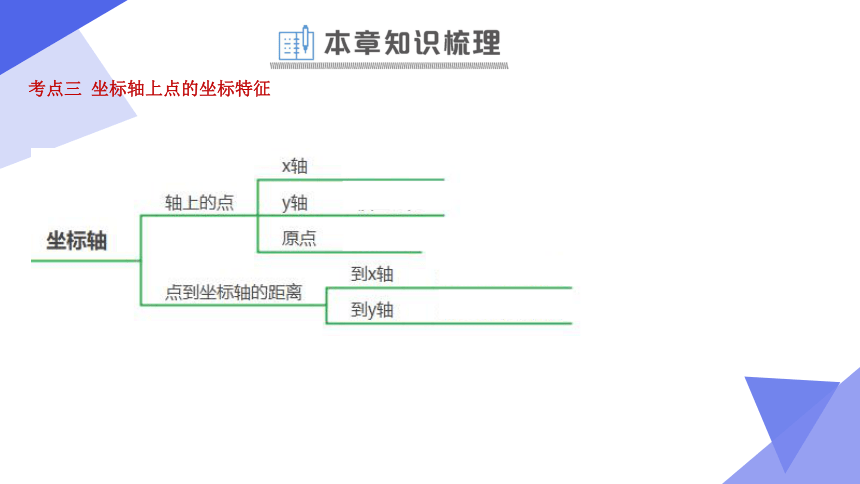
考点三 坐标轴上点的坐标特征
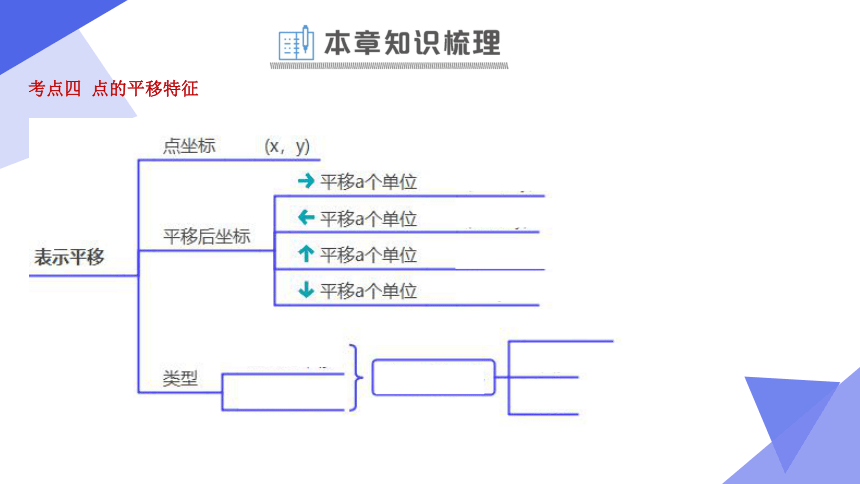
考点四 点的平移特征
考点五 对称后点的坐标特征
考点一 平面直角坐标系的相关概念
1.(21-22八年级下·山西临汾·期末)笛卡尔是法国著名的数学家,他首先提出并创建了坐标的思想,引入坐标和变量的概念,平面直角坐标系很好地体现了数学的( )
A.数形结合思想 B.类比思想 C.分类讨论思想 D.方程思想
2.(24-25八年级上·辽宁锦州·期中)以下能够比较准确表示我市某学校地理位置的是( )
A.距离九华山5千米 B.在凌海市内
C.在市政府东北方向约2千米处 D.在市政府东南方向
3.(24-25八年级上·河南郑州·期中)下列能确定郑州地理位置的是( )
A.与开封市相邻 B.北纬东经
C.在河南省 D.与洛阳直线距离
A
C
B
1.若,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点在第四象限,则a的取值为( )
A. B. C. D.任意实数
C
考点二 象限内点的坐标特征
A
3.(23-24八年级上·江苏徐州·期中)在平面直角坐标系中,点一定在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
A
4.(23-24八年级上·江苏南京·期末)平面直角坐标系中,已知点在第四象限,则m的取值范围是 .
考点三 坐标轴上点的坐标特征
1.(23-24八年级上·江苏常州·期中)已知点在x轴上,则点M到y轴的距离为 .
2.(23-24八年级上·浙江宁波·期中)已知点,试分别根据下列条件,求出的值:
(1)点在轴上;
(2)点到轴的距离为3,且在第三象限.
【详解】(1)解:∵点在轴上,
∴, 解得;
(2)∵点到轴的距离为3,
∴,
又∵点在第三象限,
∴,
解得.
考点四 点的平移特征
1.(23-24八年级上·江苏·周测)在平面直角坐标系中,把点向上平移1个单位,再向左平移2个单位,得到的点的坐标是 .
2.如图,正方形网格中的三个顶点都在格点上,建立平面直角坐标系,此时点的坐标是.若先把向右平移2个单位,再向下平移1个单位,得到.
(1)画出平移后的图形;
(2)写出平移后各顶点坐标:( ),( ),( ).
(2)平移后各顶点坐标:,,
1.(24-25八年级上·全国·期中)如图,将直角坐标系中点坐标为,点与点关于轴对称.则点的坐标是( )
A. B. C. D.
考点五 对称后点的坐标特征
2.(24-25八年级上·甘肃嘉峪关·期中)若点与点关于轴对称,则( )
A.-1 B.0 C.1 D.-7
3.(24-25八年级上·山西运城·期中)若点与点关于某条直线对称,则这条直线是()
A.轴 B.轴
C.过点且垂直于轴的直线 D.过点且平行于轴的直线
D
A
D
题型剖析
题型一:有序数对的应用
1.如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为.若小丽的座位为,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
A. B. C. D.
C
2.如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(3,4)→(4,2)→(4,0)
D.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
C
题型剖析
题型二:由已知点的坐标建立坐标系,确定其它点的坐标
1.(23-24八年级上·江苏泰州·期末)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“马”和“车”的点的坐标分别为,,则表示棋子“帅”的点的坐标 .
2.(21-22七年级下·北京西城·期中)如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示弘义阁的点的坐标为(-1,-1),表示本仁殿的点的坐标为(2,-2),则表示中海福商店的点的坐标是 .
(-4,-3)
题型剖析
题型三:点到坐标轴的距离
1.点在第二象限,它到x轴的距离是4,到y轴距离是3,则有( )
A., B., C., D.,
D
2.若在轴上,则到轴的距离是( )
A. B.1 C.2 D.3
C
3.在平面直角坐标系中,点在第三象限,且Р到x轴和y轴的距离分别为8和5,则点P的坐标为( )
A. B. C. D.
A
题型剖析
题型四:两点间的距离
1.已知点A的坐标为,点B在y轴上,当A、B两点间的距离最短时,点B的坐标为( )
A. B. C. D.
A
2.在平面直角坐标系中,有两点,若轴,则A,B两点间的距离为( )
A.1 B.2 C.3 D.4
【详解】解:∵轴,
∴A点和B点的纵坐标相等,
即a-3=-2,解得a=1,
∴A(3,-2),B(4,-2),
∴A、B两点间的距离为4-3=1.
故选:A.
题型剖析
题型四:两点间的距离
3.(23-24八年级上·江苏连云港·阶段练习)先阅读一段文字,再回答下列问题:
已知平面内两个点分别为,,其两点间距离公式为.例如:点和)的距离为.同时,当两点所在的直线在坐标轴或平行于轴或平行于轴时,两点间的距离公式可简化成:或.
(1)已知、两点在平行于轴的直线上,点的纵坐标为,点的纵坐标为,则、两点的距离为 ;
(2)线段平行于轴,且,若点的坐标为,则点的坐标是 ;
(3)已知个顶点坐标为,,,请判断此三角形的形状,并说明理由.
(1)解:设,,则 ;故答案为:;
(2)解:设,
,, ,
解得:或,则或;
故答案为:或;
(3)解:,,,
,
,
,
,且,
则为等腰直角三角形.
题型剖析
题型五:中点坐标
1.(24-25八年级上·江西景德镇·期中)在平面直角坐标系中,以任意两点,为端点的线段的中点坐标为,现有,,三点,点为线段的中点,点为点关于原点对称的点,求线段的中点坐标.
【详解】解:∵点为线段的中点,
∴,即,
∵点为点关于原点对称的点,,
∴,
∴线段的中点坐标,
∴线段的中点坐标.
题型剖析
题型六:坐标方法的简单应用
1.(24-25八年级上·陕西咸阳·期中)如图,我们把杜甫的《绝句》整齐排列放在平面直角坐标系中.
(1)“岭”和“船”的坐标依次是________________;
(2)将第2行与第3行对调(由下往上数),再将第3列与第7列对调,“雪”由开始的坐标依次变换为_______和_______;
(3)“泊”开始的坐标是,使它的坐标变换到,应该哪两行对调(由下往上数),同时哪两列对调
【详解】(1)解:“岭”的坐标是,“船”的坐标是,
故答案为:;;
(2)将第2行与第3行对调,再将第3列与第7列对调,“雪”由开始的坐标依次变换为和.
故答案为:;;
(3)“泊”开始的坐标是,使它的坐标变换到,第1行与第3行对调,同时第2列与第5列对调.
题型剖析
题型六:坐标方法的简单应用
2.(23-24七年级上·重庆·开学考试)107路公交车线路运行图如下:
(1)107路公交车从起始站出发,向______行______到达农场,再向______偏______ ______度方向行______到达公园.
(2)由市民广场向______方向行______到达政府大楼,再向______偏______ ______度方向行________到达体育馆.
(3)107路公交车从体育馆向南偏东的方向行到达终点站.请在图中画出终点站的位置.
【答案】(1)正东方向,,北,东,,
(2)正南,,北,东,,
(3)画图见解析
题型剖析
题型六:坐标方法的简单应用
3.(23-24七年级上·江苏南京·阶段练习)如图,杭州亚运会数字火炬手 和吉祥物琼琮、宸宸、莲莲在的方格每小格边长为上沿着网格线运动数字火炬手从处出发去寻找、、处的吉祥物,规定:向上向右走为正,向下向左走为负,如果从到记为:,从到记为:,其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)______,______;______,______; ______;
(2)若数字火炬手的行走路线为,则数字火炬手走过的路程为______m;
(3)若数字火炬手从处去寻找最后一棒火炬手汪顺的行走路线依次为,,,,请在图中标出最后一棒火炬手汪顺的位置点.
【详解】(1)解:根据题中的新定义得:,,;
(2)解:若数字火炬手的行走路线为,则数字火炬手走过的路程为.
(3)解:如图所示,点为火炬手汪顺的位置.
技巧突破
技巧一:计算平面直角坐标系中图形的面积
技巧突破
技巧一:计算平面直角坐标系中图形的面积
1.已知点,,点C在y正半轴上,且的面积是8,则点C的坐标为( )
A. B. C. D.
【详解】解:点C在y轴的正半轴上,点和点在x轴上,
,
的面积为8,得,
解得,点,
故选:C.
2.如图,直角坐标系中四边形的面积是( )
A.4 B.5.5 C.4.5 D.5
C
技巧突破
技巧二:点的坐标变化规律探究问题
解题方法:
1.观察平面直角坐标系中点的位置变换,探索出点的位置的循环规律;
2.对比各点的横坐标和纵坐标,探索各点横、纵坐标之间存在的规律.
技巧突破
技巧二:点的坐标变化规律探究问题
1.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头方向,每次移动一个单位长度,依次得到点,,则点的坐标是 .
【详解】解:由题意该点按“下→左→上→上→左→下”的方向每6次一循环移动的规律移动,且每移动一个循环向左移动2个单位长度,
∵,
∴点的横坐标为,且点的纵坐标与的纵坐标相同都是,
即点的坐标是.
故答案为:.
技巧突破
技巧二:点的坐标变化规律探究问题
2.如图,在平面直角坐标系中,动点从原点出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为( )
A. B.
C. D.
【详解】解:由题意得,偶数点在第一象限,
∵水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点,
∴,
∴接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点,
∴,同理可得,...
∴,
∴.
故选:D.
技巧突破
技巧二:点的坐标变化规律探究问题
3.如图,在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B、O分别落在点、处,点在x轴上,再将绕点顺时针旋转到的位置,点在x轴上,将绕点顺时针旋转到的位置,点在x轴上,依次进行下去….若点,,则点的坐标为 .
【详解】∵点,,∴,,
∴,∴,
∴的横坐标为:6,且,点的纵坐标为:2
∴的横坐标为:,点的纵坐标为:2
∴点的横坐标为:.
∴点的纵坐标为:2.
故点的坐标为.
故答案为:.
技巧突破
技巧三:平面直角坐标系中的将军饮马问题
技巧突破
技巧三:平面直角坐标系中的将军饮马问题
1.(23-24八年级上·江苏淮安·阶段练习)已知:在平面直角坐标系中的位置如图所示.
(1)的面积是 .
(2)作出关于轴对称的三角形;
(3)在轴上找到一点,使的值最小,在图中画出点.
(1)解:由题意知,,
易混易错
类型一:坐标轴上点的坐标特征混淆出错
2.若x轴上的点P到y轴的距离为3,则点P为( )
A. B.或 C. D.或
B
类型二:已知点到坐标轴上的距离求点的坐标时出错
1.在平面直角坐标系中:
(1)已知点在轴上,求点的坐标;
(2)已知两点,,若轴,点在第一象限,求的值,并确定的取值范围.
【详解】(1)根据题意知,,解得:,∴点的坐标为 .
(2)∵轴,∴,解得,
∵点在第一象限,∴,解得.
易混易错
类型三:已知坐标系内图形面积,求坐标时未注意分类讨论
3.已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是 .
【详解】解:∵点A(a,0)和点B(0,5),
∴△OAB的两边长分别为|a|与5,
∴S△OAB=,
解得:a=4或a=-4,
即a的值为±4.
故答案为:±4.
押题预测
1. 数学课上,陈老师在黑板上画出一个正方形被等分成4行4列,如图所示,她问大家几个问题,你能解答出来吗?
(1)若A点用表示,B点用表示,C点用表示,则C点在哪里?请在图(1)中标出,D点如何表示呢?
(2)若A点用表示,B点用表示,C点用表示,则C点在哪里?请在图(2)中标出,D点如何表示呢?
押题预测
2.(22-23八年级上·安徽淮北·期末)在平面直角坐标系中,某点按向下、向右、向上、向右的方向依次不断移动,每次移动1个单位长度,其运动路线如图所示,根据图形规律,解决下列问题
(1)点的坐标为___________,点的坐标为___________,点的坐标为___________,点的坐标为___________.
(2)直接写出点到点的距离:___________.
【详解】(1)解:根据题意得:点的坐标为;
点的坐标为;
点的坐标为;
……
由此发现,点的坐标为;
故答案为:;;;;
(2)解:∵,
∴点的坐标为,即,
∵点的坐标为,
∴点到点的距离1012.
故答案为:1012
押题预测
3.(24-25八年级上·陕西西安·期末)梯形在平面直角坐标系中的位置如图,已知,点,,,其中满足.
(1)直接写出___________;
(2)求点,的坐标;
(3)若在第二象限有一点,连接,,已知的面积是面积的一半,求点的坐标.
(1)解:∵,∴,则,
故答案为:;
(2)解:由()得,,∴,∴,
∴,∴,
∴,,
∴点的坐标为,点的坐标为;
押题预测
3.(24-25八年级上·陕西西安·期末)梯形在平面直角坐标系中的位置如图,已知,点,,,其中满足.
(1)直接写出___________;
(2)求点,的坐标;
(3)若在第二象限有一点,连接,,已知的面积是面积的一半,求点的坐标.
(3)解:∵,,∴,
∴,
∵,的面积是面积的一半,
∴,∴,
∴点的坐标为.
押题预测
4.( 23-24八年级上·黑龙江齐齐哈尔·期末)在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“龙沙点”.
(1)点的“长距”为______;
(2)若点是“龙沙点”,求的值:
(3)若点的长距为,且点在第二象限内,点的坐标为,试说明:点是“龙沙点”
【详解】(1)∵点到轴、轴的距离的较大值称为点的“长距”,
∴点到轴的距离为:;到轴的距离为,
∴点的“长距”为.
故答案为:.
2)∵点到轴、轴的距离相等时,称点为“龙沙点”,
∴当点是“龙沙点”,,
∴,
当,解得:;
当,解得:;
∴或.
押题预测
4.(23-24八年级上·黑龙江齐齐哈尔·期末)在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“龙沙点”.
(1)点的“长距”为______;
(2)若点是“龙沙点”,求的值:
(3)若点的长距为,且点在第二象限内,点的坐标为,试说明:点是“龙沙点”
(3)∵点的长距为,
∴,解得:或;
∵在第二象限内,∴,∴,
∵点的坐标为,
∴点,
∵,
∴点是“龙沙点”.
八年级数学上学期·期末复习大串讲
专题05 平面直角坐标系
苏科版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
5大常考点:知识梳理
6大题型典例剖析+3大技巧
3大易错易混经典例题
精选4道期末真题对应考点练
目录
考点一 平面直角坐标系的相关概念
考点二 象限内点的坐标特征
考点三 坐标轴上点的坐标特征
考点四 点的平移特征
考点五 对称后点的坐标特征
考点一 平面直角坐标系的相关概念
1.(21-22八年级下·山西临汾·期末)笛卡尔是法国著名的数学家,他首先提出并创建了坐标的思想,引入坐标和变量的概念,平面直角坐标系很好地体现了数学的( )
A.数形结合思想 B.类比思想 C.分类讨论思想 D.方程思想
2.(24-25八年级上·辽宁锦州·期中)以下能够比较准确表示我市某学校地理位置的是( )
A.距离九华山5千米 B.在凌海市内
C.在市政府东北方向约2千米处 D.在市政府东南方向
3.(24-25八年级上·河南郑州·期中)下列能确定郑州地理位置的是( )
A.与开封市相邻 B.北纬东经
C.在河南省 D.与洛阳直线距离
A
C
B
1.若,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点在第四象限,则a的取值为( )
A. B. C. D.任意实数
C
考点二 象限内点的坐标特征
A
3.(23-24八年级上·江苏徐州·期中)在平面直角坐标系中,点一定在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
A
4.(23-24八年级上·江苏南京·期末)平面直角坐标系中,已知点在第四象限,则m的取值范围是 .
考点三 坐标轴上点的坐标特征
1.(23-24八年级上·江苏常州·期中)已知点在x轴上,则点M到y轴的距离为 .
2.(23-24八年级上·浙江宁波·期中)已知点,试分别根据下列条件,求出的值:
(1)点在轴上;
(2)点到轴的距离为3,且在第三象限.
【详解】(1)解:∵点在轴上,
∴, 解得;
(2)∵点到轴的距离为3,
∴,
又∵点在第三象限,
∴,
解得.
考点四 点的平移特征
1.(23-24八年级上·江苏·周测)在平面直角坐标系中,把点向上平移1个单位,再向左平移2个单位,得到的点的坐标是 .
2.如图,正方形网格中的三个顶点都在格点上,建立平面直角坐标系,此时点的坐标是.若先把向右平移2个单位,再向下平移1个单位,得到.
(1)画出平移后的图形;
(2)写出平移后各顶点坐标:( ),( ),( ).
(2)平移后各顶点坐标:,,
1.(24-25八年级上·全国·期中)如图,将直角坐标系中点坐标为,点与点关于轴对称.则点的坐标是( )
A. B. C. D.
考点五 对称后点的坐标特征
2.(24-25八年级上·甘肃嘉峪关·期中)若点与点关于轴对称,则( )
A.-1 B.0 C.1 D.-7
3.(24-25八年级上·山西运城·期中)若点与点关于某条直线对称,则这条直线是()
A.轴 B.轴
C.过点且垂直于轴的直线 D.过点且平行于轴的直线
D
A
D
题型剖析
题型一:有序数对的应用
1.如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为.若小丽的座位为,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
A. B. C. D.
C
2.如图,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,则小明走下列线路不能到达学校的是( )
A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(3,4)→(4,2)→(4,0)
D.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
C
题型剖析
题型二:由已知点的坐标建立坐标系,确定其它点的坐标
1.(23-24八年级上·江苏泰州·期末)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“马”和“车”的点的坐标分别为,,则表示棋子“帅”的点的坐标 .
2.(21-22七年级下·北京西城·期中)如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示弘义阁的点的坐标为(-1,-1),表示本仁殿的点的坐标为(2,-2),则表示中海福商店的点的坐标是 .
(-4,-3)
题型剖析
题型三:点到坐标轴的距离
1.点在第二象限,它到x轴的距离是4,到y轴距离是3,则有( )
A., B., C., D.,
D
2.若在轴上,则到轴的距离是( )
A. B.1 C.2 D.3
C
3.在平面直角坐标系中,点在第三象限,且Р到x轴和y轴的距离分别为8和5,则点P的坐标为( )
A. B. C. D.
A
题型剖析
题型四:两点间的距离
1.已知点A的坐标为,点B在y轴上,当A、B两点间的距离最短时,点B的坐标为( )
A. B. C. D.
A
2.在平面直角坐标系中,有两点,若轴,则A,B两点间的距离为( )
A.1 B.2 C.3 D.4
【详解】解:∵轴,
∴A点和B点的纵坐标相等,
即a-3=-2,解得a=1,
∴A(3,-2),B(4,-2),
∴A、B两点间的距离为4-3=1.
故选:A.
题型剖析
题型四:两点间的距离
3.(23-24八年级上·江苏连云港·阶段练习)先阅读一段文字,再回答下列问题:
已知平面内两个点分别为,,其两点间距离公式为.例如:点和)的距离为.同时,当两点所在的直线在坐标轴或平行于轴或平行于轴时,两点间的距离公式可简化成:或.
(1)已知、两点在平行于轴的直线上,点的纵坐标为,点的纵坐标为,则、两点的距离为 ;
(2)线段平行于轴,且,若点的坐标为,则点的坐标是 ;
(3)已知个顶点坐标为,,,请判断此三角形的形状,并说明理由.
(1)解:设,,则 ;故答案为:;
(2)解:设,
,, ,
解得:或,则或;
故答案为:或;
(3)解:,,,
,
,
,
,且,
则为等腰直角三角形.
题型剖析
题型五:中点坐标
1.(24-25八年级上·江西景德镇·期中)在平面直角坐标系中,以任意两点,为端点的线段的中点坐标为,现有,,三点,点为线段的中点,点为点关于原点对称的点,求线段的中点坐标.
【详解】解:∵点为线段的中点,
∴,即,
∵点为点关于原点对称的点,,
∴,
∴线段的中点坐标,
∴线段的中点坐标.
题型剖析
题型六:坐标方法的简单应用
1.(24-25八年级上·陕西咸阳·期中)如图,我们把杜甫的《绝句》整齐排列放在平面直角坐标系中.
(1)“岭”和“船”的坐标依次是________________;
(2)将第2行与第3行对调(由下往上数),再将第3列与第7列对调,“雪”由开始的坐标依次变换为_______和_______;
(3)“泊”开始的坐标是,使它的坐标变换到,应该哪两行对调(由下往上数),同时哪两列对调
【详解】(1)解:“岭”的坐标是,“船”的坐标是,
故答案为:;;
(2)将第2行与第3行对调,再将第3列与第7列对调,“雪”由开始的坐标依次变换为和.
故答案为:;;
(3)“泊”开始的坐标是,使它的坐标变换到,第1行与第3行对调,同时第2列与第5列对调.
题型剖析
题型六:坐标方法的简单应用
2.(23-24七年级上·重庆·开学考试)107路公交车线路运行图如下:
(1)107路公交车从起始站出发,向______行______到达农场,再向______偏______ ______度方向行______到达公园.
(2)由市民广场向______方向行______到达政府大楼,再向______偏______ ______度方向行________到达体育馆.
(3)107路公交车从体育馆向南偏东的方向行到达终点站.请在图中画出终点站的位置.
【答案】(1)正东方向,,北,东,,
(2)正南,,北,东,,
(3)画图见解析
题型剖析
题型六:坐标方法的简单应用
3.(23-24七年级上·江苏南京·阶段练习)如图,杭州亚运会数字火炬手 和吉祥物琼琮、宸宸、莲莲在的方格每小格边长为上沿着网格线运动数字火炬手从处出发去寻找、、处的吉祥物,规定:向上向右走为正,向下向左走为负,如果从到记为:,从到记为:,其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)______,______;______,______; ______;
(2)若数字火炬手的行走路线为,则数字火炬手走过的路程为______m;
(3)若数字火炬手从处去寻找最后一棒火炬手汪顺的行走路线依次为,,,,请在图中标出最后一棒火炬手汪顺的位置点.
【详解】(1)解:根据题中的新定义得:,,;
(2)解:若数字火炬手的行走路线为,则数字火炬手走过的路程为.
(3)解:如图所示,点为火炬手汪顺的位置.
技巧突破
技巧一:计算平面直角坐标系中图形的面积
技巧突破
技巧一:计算平面直角坐标系中图形的面积
1.已知点,,点C在y正半轴上,且的面积是8,则点C的坐标为( )
A. B. C. D.
【详解】解:点C在y轴的正半轴上,点和点在x轴上,
,
的面积为8,得,
解得,点,
故选:C.
2.如图,直角坐标系中四边形的面积是( )
A.4 B.5.5 C.4.5 D.5
C
技巧突破
技巧二:点的坐标变化规律探究问题
解题方法:
1.观察平面直角坐标系中点的位置变换,探索出点的位置的循环规律;
2.对比各点的横坐标和纵坐标,探索各点横、纵坐标之间存在的规律.
技巧突破
技巧二:点的坐标变化规律探究问题
1.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头方向,每次移动一个单位长度,依次得到点,,则点的坐标是 .
【详解】解:由题意该点按“下→左→上→上→左→下”的方向每6次一循环移动的规律移动,且每移动一个循环向左移动2个单位长度,
∵,
∴点的横坐标为,且点的纵坐标与的纵坐标相同都是,
即点的坐标是.
故答案为:.
技巧突破
技巧二:点的坐标变化规律探究问题
2.如图,在平面直角坐标系中,动点从原点出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点,…,按此作法进行下去,则点的坐标为( )
A. B.
C. D.
【详解】解:由题意得,偶数点在第一象限,
∵水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点,
∴,
∴接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点,
∴,同理可得,...
∴,
∴.
故选:D.
技巧突破
技巧二:点的坐标变化规律探究问题
3.如图,在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B、O分别落在点、处,点在x轴上,再将绕点顺时针旋转到的位置,点在x轴上,将绕点顺时针旋转到的位置,点在x轴上,依次进行下去….若点,,则点的坐标为 .
【详解】∵点,,∴,,
∴,∴,
∴的横坐标为:6,且,点的纵坐标为:2
∴的横坐标为:,点的纵坐标为:2
∴点的横坐标为:.
∴点的纵坐标为:2.
故点的坐标为.
故答案为:.
技巧突破
技巧三:平面直角坐标系中的将军饮马问题
技巧突破
技巧三:平面直角坐标系中的将军饮马问题
1.(23-24八年级上·江苏淮安·阶段练习)已知:在平面直角坐标系中的位置如图所示.
(1)的面积是 .
(2)作出关于轴对称的三角形;
(3)在轴上找到一点,使的值最小,在图中画出点.
(1)解:由题意知,,
易混易错
类型一:坐标轴上点的坐标特征混淆出错
2.若x轴上的点P到y轴的距离为3,则点P为( )
A. B.或 C. D.或
B
类型二:已知点到坐标轴上的距离求点的坐标时出错
1.在平面直角坐标系中:
(1)已知点在轴上,求点的坐标;
(2)已知两点,,若轴,点在第一象限,求的值,并确定的取值范围.
【详解】(1)根据题意知,,解得:,∴点的坐标为 .
(2)∵轴,∴,解得,
∵点在第一象限,∴,解得.
易混易错
类型三:已知坐标系内图形面积,求坐标时未注意分类讨论
3.已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是 .
【详解】解:∵点A(a,0)和点B(0,5),
∴△OAB的两边长分别为|a|与5,
∴S△OAB=,
解得:a=4或a=-4,
即a的值为±4.
故答案为:±4.
押题预测
1. 数学课上,陈老师在黑板上画出一个正方形被等分成4行4列,如图所示,她问大家几个问题,你能解答出来吗?
(1)若A点用表示,B点用表示,C点用表示,则C点在哪里?请在图(1)中标出,D点如何表示呢?
(2)若A点用表示,B点用表示,C点用表示,则C点在哪里?请在图(2)中标出,D点如何表示呢?
押题预测
2.(22-23八年级上·安徽淮北·期末)在平面直角坐标系中,某点按向下、向右、向上、向右的方向依次不断移动,每次移动1个单位长度,其运动路线如图所示,根据图形规律,解决下列问题
(1)点的坐标为___________,点的坐标为___________,点的坐标为___________,点的坐标为___________.
(2)直接写出点到点的距离:___________.
【详解】(1)解:根据题意得:点的坐标为;
点的坐标为;
点的坐标为;
……
由此发现,点的坐标为;
故答案为:;;;;
(2)解:∵,
∴点的坐标为,即,
∵点的坐标为,
∴点到点的距离1012.
故答案为:1012
押题预测
3.(24-25八年级上·陕西西安·期末)梯形在平面直角坐标系中的位置如图,已知,点,,,其中满足.
(1)直接写出___________;
(2)求点,的坐标;
(3)若在第二象限有一点,连接,,已知的面积是面积的一半,求点的坐标.
(1)解:∵,∴,则,
故答案为:;
(2)解:由()得,,∴,∴,
∴,∴,
∴,,
∴点的坐标为,点的坐标为;
押题预测
3.(24-25八年级上·陕西西安·期末)梯形在平面直角坐标系中的位置如图,已知,点,,,其中满足.
(1)直接写出___________;
(2)求点,的坐标;
(3)若在第二象限有一点,连接,,已知的面积是面积的一半,求点的坐标.
(3)解:∵,,∴,
∴,
∵,的面积是面积的一半,
∴,∴,
∴点的坐标为.
押题预测
4.( 23-24八年级上·黑龙江齐齐哈尔·期末)在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“龙沙点”.
(1)点的“长距”为______;
(2)若点是“龙沙点”,求的值:
(3)若点的长距为,且点在第二象限内,点的坐标为,试说明:点是“龙沙点”
【详解】(1)∵点到轴、轴的距离的较大值称为点的“长距”,
∴点到轴的距离为:;到轴的距离为,
∴点的“长距”为.
故答案为:.
2)∵点到轴、轴的距离相等时,称点为“龙沙点”,
∴当点是“龙沙点”,,
∴,
当,解得:;
当,解得:;
∴或.
押题预测
4.(23-24八年级上·黑龙江齐齐哈尔·期末)在平面直角坐标系中,给出如下定义:点到轴、轴的距离的较大值称为点的“长距”,点到轴、轴的距离相等时,称点为“龙沙点”.
(1)点的“长距”为______;
(2)若点是“龙沙点”,求的值:
(3)若点的长距为,且点在第二象限内,点的坐标为,试说明:点是“龙沙点”
(3)∵点的长距为,
∴,解得:或;
∵在第二象限内,∴,∴,
∵点的坐标为,
∴点,
∵,
∴点是“龙沙点”.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
