2024-2025学年内蒙古赤峰市名校高二(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年内蒙古赤峰市名校高二(上)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 103.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 14:58:21 | ||
图片预览



文档简介
2024-2025学年内蒙古赤峰市名校高二(上)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.关于空间向量,,,下列运算错误的是( )
A. B.
C. D.
2.某生物实验室有种月季花种子,其中开红色花的种子有颗,开粉色花的种子有颗,开橙色花的种子有颗从这些种子中任意选取颗,则这颗种子对应开花的颜色为橙色的概率为( )
A. B. C. D.
3.在正方体中,下列向量与平行的是( )
A. B. C. D.
4.若数据,,,的方差为,则数据,,,的方差为( )
A. B. C. D.
5.如图,在直三棱柱中,,分别为棱,的中点,设,,,则( )
A.
B.
C.
D.
6.已知点,,,则点到直线的距离为( )
A. B. C. D.
7.在正四面体中,为棱的中点,,则( )
A. B. C. D.
8.金秋十月,某校举行运动会,甲、乙两名同学均从跳高、跳远、米跑和米跑这四个项目中选择两个项目参加设事件“甲、乙两人所选项目恰有一个相同”,事件“甲、乙两人所选项目完全不同”,事件“甲、乙两人所选项目完全相同”,事件“甲、乙两人均未选择米跑项目”,则( )
A. 与是对立事件 B. 与相互独立 C. 与相互独立 D. 与不互斥
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知空间向量,,,则( )
A. B.
C. D. 在方向上的投影向量为
10.降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失,而在水平面上积聚的水层深度,一般以毫米为单位降雨量可以直观地反映一个地区某一时间段内降水的多少,它对农业生产、水利工程、城市排水等有着重要的影响如图,这是,两地某年上半年每月降雨量的折线统计图.
下列结论正确的是( )
A. 这年上半年地月平均降雨量比地月平均降雨量大
B. 这年上半年地月降雨量的中位数比地月降雨量的中位数大
C. 这年上半年地月降雨量的极差比地月降雨量的极差大
D. 这年上半年地月降雨量的分位数比地月平均降雨量的分位数大
11.在空间直角坐标系中,已知,,,,,,则( )
A. 为质数 B. 为直角三角形
C. 与所成角的正弦值为 D. 几何体的体积为
三、填空题:本题共3小题,每小题5分,共15分。
12.若一组数据为,,,,,,,,,,则这组数据的众数为______.
13.若平面的一个法向量为,平面的一个法向量为,则与的夹角为______.
14.在如表所示的方格表中选个方格,若要求每行和每列都恰有个方格被选中,则被选方格的个数之和的最大值为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
在空间直角坐标系中,已知,,,.
若,求的值;
若,求的值.
16.本小题分
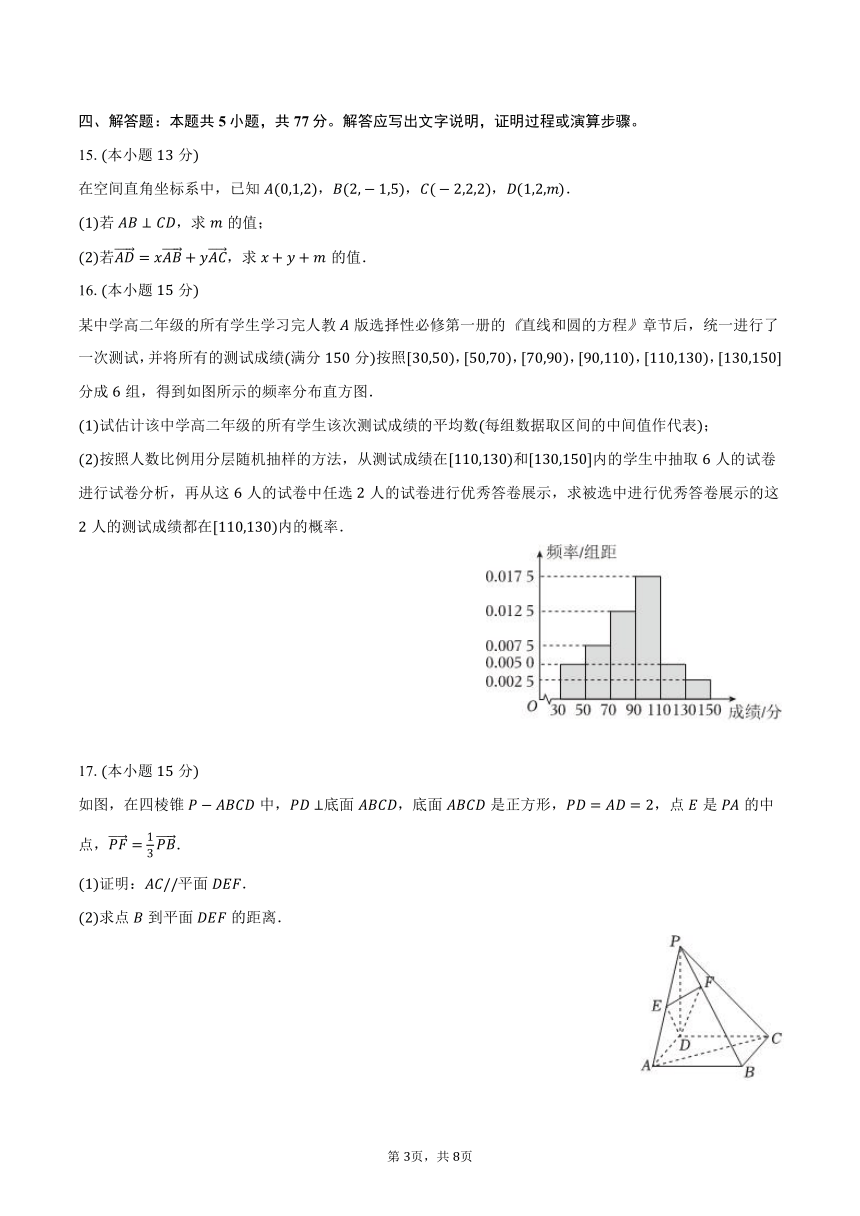
某中学高二年级的所有学生学习完人教版选择性必修第一册的直线和圆的方程章节后,统一进行了一次测试,并将所有的测试成绩满分分按照,,,,,分成组,得到如图所示的频率分布直方图.
试估计该中学高二年级的所有学生该次测试成绩的平均数每组数据取区间的中间值作代表;
按照人数比例用分层随机抽样的方法,从测试成绩在和内的学生中抽取人的试卷进行试卷分析,再从这人的试卷中任选人的试卷进行优秀答卷展示,求被选中进行优秀答卷展示的这人的测试成绩都在内的概率.
17.本小题分
如图,在四棱锥中,底面,底面是正方形,,点是的中点,.
证明:平面.
求点到平面的距离.
18.本小题分
,,三人参加知识闯关比赛,三人闯关成功与否相互独立已知闯关成功的概率是,,,三人闯关都不成功的概率是,,,三人闯关都成功的概率是.
求,两人各自闯关成功的概率;
求,,三人中恰有两人闯关成功的概率.
19.本小题分
如图,在四棱台中,底面是正方形,,平面.
证明:平面;
求直线与平面所成角的正弦值.
棱上是否存在一点,使得二面角的余弦值为?若存在,求线段的长;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:,,
因为,所以,
即,解得.
,,
因为,所以,
解得,
则.
16.解:根据题意可得测试成绩的平均数约为:
分;
测试成绩在和内的频率之比为:,
在和内分别抽人的试卷,人的试卷,
再从这人的试卷中任选人的试卷共有种不同结果,
而这人的测试成绩都在内包含种不同结果,
所求概率为.
17.证明:因为底面,底面是正方形,,点是的中点,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,,,,,
所以,,,
设是平面的法向量,,,
则,
令,得,
因为,
所以,
又因为平面,
所以平面;
解:连接,,
可得点到平面的距离.
18.解:根据题意,设,两人各自闯关成功的概率分别是,,
闯关成功的概率是,,,三人闯关都不成功的概率是,,,三人闯关都成功的概率是,
则有,解可得,
所以,两人各自闯关成功的概率分别是,.
根据题意,分种情况讨论:
只有、闯关成功的概率;
只有、闯关成功的概率;
只有、闯关成功的概率.
故A,,三人中恰有两人闯关成功的概率为.
19.解:证明:因为底面是正方形,所以,
又因为平面,平面,所以,
因为,且,平面,
所以平面.
因为平面,,平面,
所以,,
又底面是正方形,,
故AB,,两两垂直,
以,,所在直线分别为,,轴,建立如图所示的空间直角坐标系,
则,,,,,,
所以,,,
设平面的法向量为,
则,则,
解得,令,则,
故,
设直线与平面所成的角为,
则,
故直线与平面所成角的正弦值为.
若存在点满足题意,则可设点,其中,
则,.
设平面的法向量为,
则,则
令,则,,
故.
易得平面的一个法向量为,
所以,
解得或舍去,
故棱上存在一点,当时,二面角的余弦值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.关于空间向量,,,下列运算错误的是( )
A. B.
C. D.
2.某生物实验室有种月季花种子,其中开红色花的种子有颗,开粉色花的种子有颗,开橙色花的种子有颗从这些种子中任意选取颗,则这颗种子对应开花的颜色为橙色的概率为( )
A. B. C. D.
3.在正方体中,下列向量与平行的是( )
A. B. C. D.
4.若数据,,,的方差为,则数据,,,的方差为( )
A. B. C. D.
5.如图,在直三棱柱中,,分别为棱,的中点,设,,,则( )
A.
B.
C.
D.
6.已知点,,,则点到直线的距离为( )
A. B. C. D.
7.在正四面体中,为棱的中点,,则( )
A. B. C. D.
8.金秋十月,某校举行运动会,甲、乙两名同学均从跳高、跳远、米跑和米跑这四个项目中选择两个项目参加设事件“甲、乙两人所选项目恰有一个相同”,事件“甲、乙两人所选项目完全不同”,事件“甲、乙两人所选项目完全相同”,事件“甲、乙两人均未选择米跑项目”,则( )
A. 与是对立事件 B. 与相互独立 C. 与相互独立 D. 与不互斥
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知空间向量,,,则( )
A. B.
C. D. 在方向上的投影向量为
10.降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失,而在水平面上积聚的水层深度,一般以毫米为单位降雨量可以直观地反映一个地区某一时间段内降水的多少,它对农业生产、水利工程、城市排水等有着重要的影响如图,这是,两地某年上半年每月降雨量的折线统计图.
下列结论正确的是( )
A. 这年上半年地月平均降雨量比地月平均降雨量大
B. 这年上半年地月降雨量的中位数比地月降雨量的中位数大
C. 这年上半年地月降雨量的极差比地月降雨量的极差大
D. 这年上半年地月降雨量的分位数比地月平均降雨量的分位数大
11.在空间直角坐标系中,已知,,,,,,则( )
A. 为质数 B. 为直角三角形
C. 与所成角的正弦值为 D. 几何体的体积为
三、填空题:本题共3小题,每小题5分,共15分。
12.若一组数据为,,,,,,,,,,则这组数据的众数为______.
13.若平面的一个法向量为,平面的一个法向量为,则与的夹角为______.
14.在如表所示的方格表中选个方格,若要求每行和每列都恰有个方格被选中,则被选方格的个数之和的最大值为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
在空间直角坐标系中,已知,,,.
若,求的值;
若,求的值.
16.本小题分
某中学高二年级的所有学生学习完人教版选择性必修第一册的直线和圆的方程章节后,统一进行了一次测试,并将所有的测试成绩满分分按照,,,,,分成组,得到如图所示的频率分布直方图.
试估计该中学高二年级的所有学生该次测试成绩的平均数每组数据取区间的中间值作代表;
按照人数比例用分层随机抽样的方法,从测试成绩在和内的学生中抽取人的试卷进行试卷分析,再从这人的试卷中任选人的试卷进行优秀答卷展示,求被选中进行优秀答卷展示的这人的测试成绩都在内的概率.
17.本小题分
如图,在四棱锥中,底面,底面是正方形,,点是的中点,.
证明:平面.
求点到平面的距离.
18.本小题分
,,三人参加知识闯关比赛,三人闯关成功与否相互独立已知闯关成功的概率是,,,三人闯关都不成功的概率是,,,三人闯关都成功的概率是.
求,两人各自闯关成功的概率;
求,,三人中恰有两人闯关成功的概率.
19.本小题分
如图,在四棱台中,底面是正方形,,平面.
证明:平面;
求直线与平面所成角的正弦值.
棱上是否存在一点,使得二面角的余弦值为?若存在,求线段的长;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:,,
因为,所以,
即,解得.
,,
因为,所以,
解得,
则.
16.解:根据题意可得测试成绩的平均数约为:
分;
测试成绩在和内的频率之比为:,
在和内分别抽人的试卷,人的试卷,
再从这人的试卷中任选人的试卷共有种不同结果,
而这人的测试成绩都在内包含种不同结果,
所求概率为.
17.证明:因为底面,底面是正方形,,点是的中点,,
以为坐标原点,建立如图所示的空间直角坐标系,
则,,,,,
所以,,,
设是平面的法向量,,,
则,
令,得,
因为,
所以,
又因为平面,
所以平面;
解:连接,,
可得点到平面的距离.
18.解:根据题意,设,两人各自闯关成功的概率分别是,,
闯关成功的概率是,,,三人闯关都不成功的概率是,,,三人闯关都成功的概率是,
则有,解可得,
所以,两人各自闯关成功的概率分别是,.
根据题意,分种情况讨论:
只有、闯关成功的概率;
只有、闯关成功的概率;
只有、闯关成功的概率.
故A,,三人中恰有两人闯关成功的概率为.
19.解:证明:因为底面是正方形,所以,
又因为平面,平面,所以,
因为,且,平面,
所以平面.
因为平面,,平面,
所以,,
又底面是正方形,,
故AB,,两两垂直,
以,,所在直线分别为,,轴,建立如图所示的空间直角坐标系,
则,,,,,,
所以,,,
设平面的法向量为,
则,则,
解得,令,则,
故,
设直线与平面所成的角为,
则,
故直线与平面所成角的正弦值为.
若存在点满足题意,则可设点,其中,
则,.
设平面的法向量为,
则,则
令,则,,
故.
易得平面的一个法向量为,
所以,
解得或舍去,
故棱上存在一点,当时,二面角的余弦值为.
第1页,共1页
同课章节目录
