2016北师大版数学必修二教学设计:1.5.1平行关系的判定
文档属性
| 名称 | 2016北师大版数学必修二教学设计:1.5.1平行关系的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 142.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-24 17:34:15 | ||
图片预览

文档简介
5.1平行关系的判定
一、教材的地位与作用
平行关系的判定是在线与线、线与面、面与面 ( http: / / www.21cnjy.com )的知识结构中起着承上启下的作用,也是今后学习共面向量的基础。在此之前,学生已学习了空间两直线的位置关系,这为过渡到本节的学习起着铺垫作用。本节的主要内容有直线和平面的三种位置关系和直线与平面平行的判定两部分。平行关系是全章的主要内容之一,而直线与平面平行的判定是平行关系的初步。因此,在立体几何中,占据重要的地位。
二、教学目标
1.知识与技能: (1)理解并掌握线面平行、面面平行的判定定理及其应用;
(2)能将数学三种语言(自然语言、图形语言、符号语言)相互转化
2. 过程与方法:借助已有知识,通过观 ( http: / / www.21cnjy.com )察模型,抽象概况出线面平行、面面平行的定义,类比线面平探索面面平行的判定定理, 培养学生的划归思想、空间想象力和抽象概括能力
3.情感态度与价值观:在学习过程中,使学生获得积极的情感,培养数学学习的兴趣
三、教学重难点
教学重点:线面平行和平面与平面平行的定义和判定定理
教学难点:线面平行和平面与平面平行的判定定理的推导和应用
四、教法学法:
采用直观类比法、探究发现法、观察实验法等教 ( http: / / www.21cnjy.com )学方法,教师通过创设问题探究,引导学生通过直观感知,操作确认逐步发现知识的形成过程,使教学活动真正建立在学生自主活动和探究的基础上,着力培养学生的抽象概括能力和空间想象能力.
五、教学过程
(一)温故知新:
复习回顾
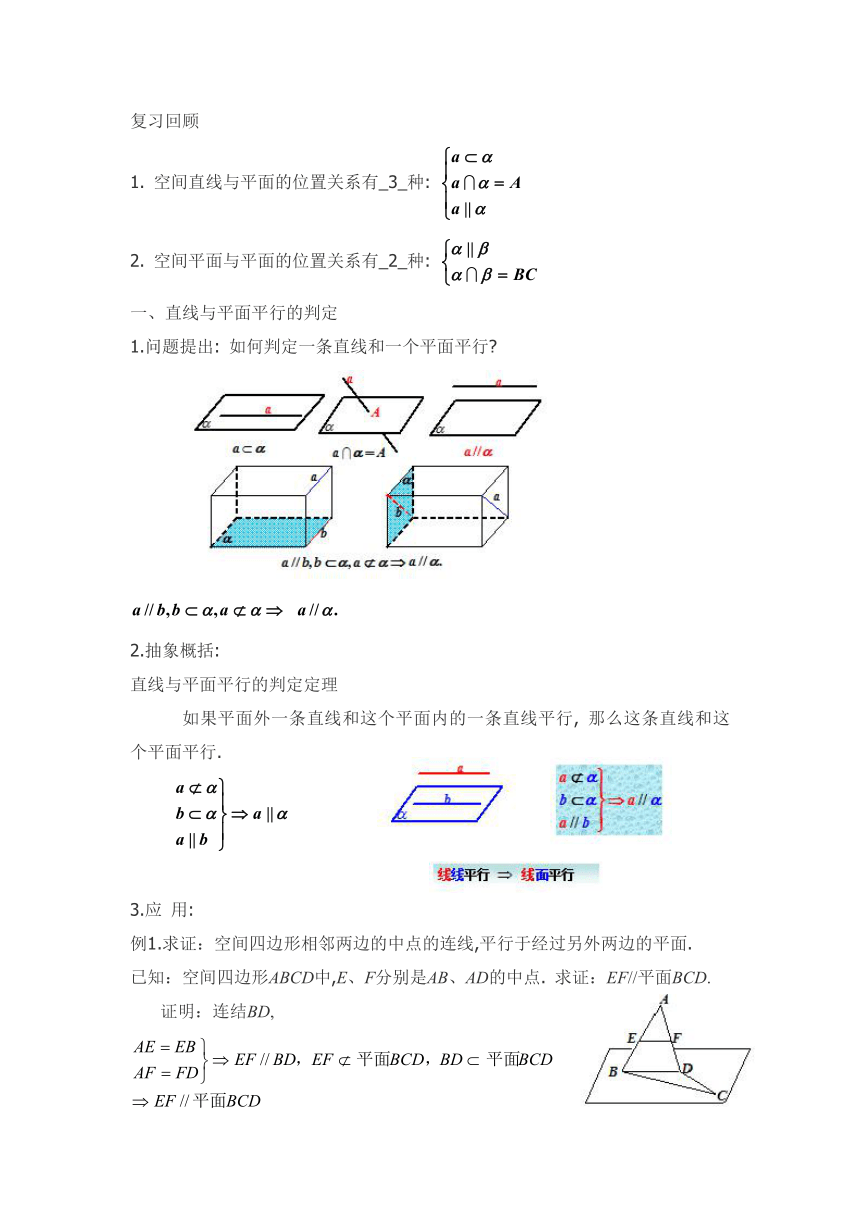
1. 空间直线与平面的位置关系有_3_种:
2. 空间平面与平面的位置关系有_2_种:
一、直线与平面平行的判定
1.问题提出: 如何判定一条直线和一个平面平行
( http: / / www.21cnjy.com )
2.抽象概括:
直线与平面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行.
3.应 用:
例1.求证:空间四边形相邻两边的中点的连线,平行于经过另外两边的平面.
已知:空间四边形ABCD中,E、F分别是AB、AD的中点. 求证:EF//平面BCD.
证明:连结BD,
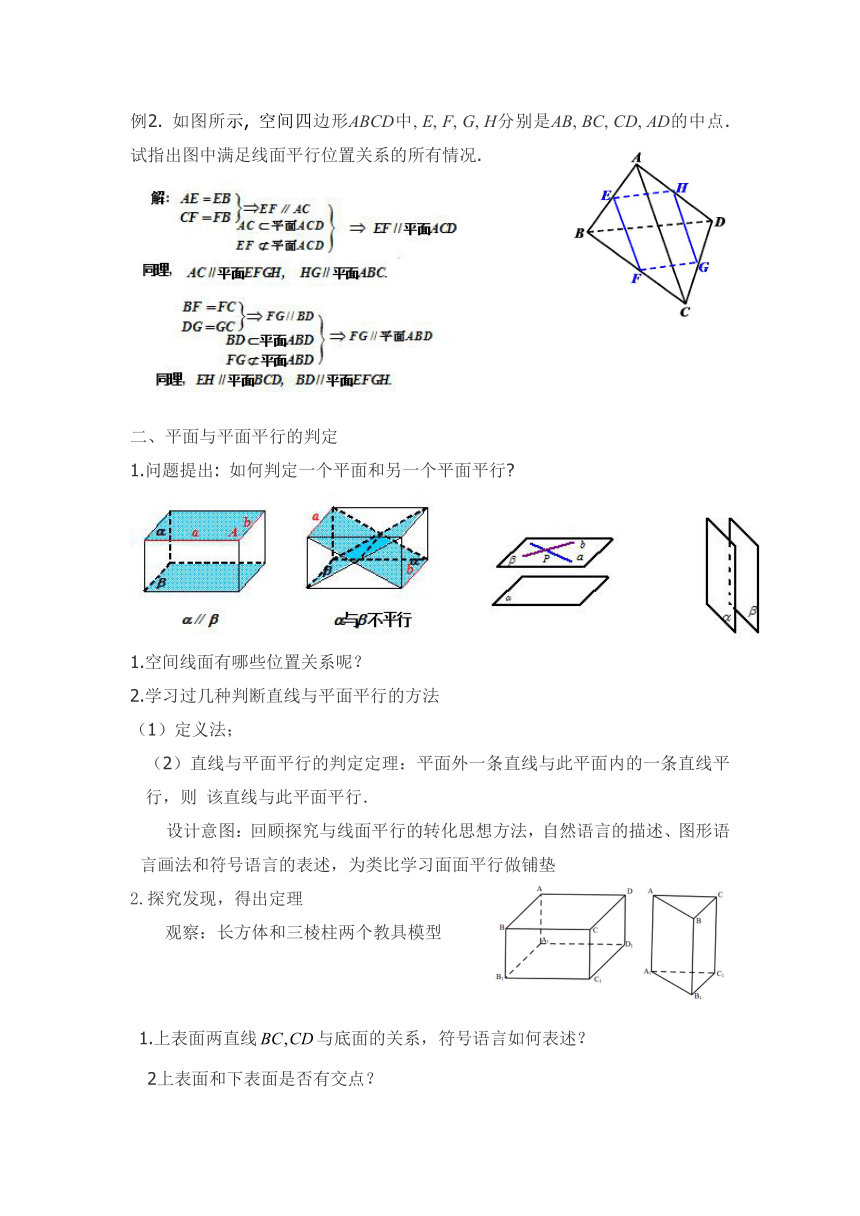
例2. 如图所示, 空间四 ( http: / / www.21cnjy.com )边形ABCD中, E, F, G, H分别是AB, BC, CD, AD的中点. 试指出图中满足线面平行位置关系的所有情况.
( http: / / www.21cnjy.com )
二、平面与平面平行的判定
1.问题提出: 如何判定一个平面和另一个平面平行
( http: / / www.21cnjy.com )
1.空间线面有哪些位置关系呢?
2.学习过几种判断直线与平面平行的方法
(1)定义法;
(2)直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则 该直线与此平面平行.
设计意图:回顾探究与线面平行的转化思想方法,自然语言的描述、图形语言画法和符号语言的表述,为类比学习面面平行做铺垫
2.探究发现,得出定理
观察:长方体和三棱柱两个教具模型
1.上表面两直线与底面的关系,符号语言如何表述?
2上表面和下表面是否有交点?
抽象概况出面面平行的定义:①,②记作: ③ 图形如何画?
设计意图:由线面平行定义直观映射出面面平行的定义,从直观过渡到抽象推理.
探究活动1:①将长方体和三棱柱平移和旋转,上下地面是否还平行?
②将长方体底面的边和三棱柱底面顶点抬起是否上表面平行桌面?
探究活动2: 1、平面内有一条直线与平面平行, 则平面,平行吗?
2、平面内有两条直线与平面平行,平面,平行吗?
3、平面内有无数条直线与平面平行,平面,平行吗?
设计意图: 由知识回顾到问题提出很自然 ( http: / / www.21cnjy.com )。以疑导思,使学生在问题带动下进行更加主动的思维活动,经历从实际背景中抽象出数学模型、从现实的生活空间中抽象出几何图形和几何问题的过程,注重探索空间图形性质的过程。 由现实生活抽象到数学知识 以问题的形式让学生小组探讨,激发学生的探索欲望,营造一个让学生主动观察、思考、讨论的氛围。
学生在实例的探究中,思考并寻找平面与平面平行的判定条件是什么,从而概括提炼出平面与平面平行的判定定理。
2.抽象概括:平面与平面平行的判定定理:
如果一个平面内有两条相交直线都平行于另一个平面, 那么这两个平面平行.
3.应 用:
总结思路,体会思想 :面面平行--线面平行--线线平行 。
设计意图:通过实际问题探究、讨论,思辨,及时巩固定理,运用定理,培养学生的识图能力与逻辑推理能力,同时体会转化思想。
三、反馈练习
1. 过直线外一点与该直线平行的平面有__无数__个. 过平面外一点与该平面平行的直线有_无数___条.
2.平行四边形ABCD和平行四边形CDEF有一公共边CD, 它们不在同一平面内, M为FC的中点. 求证: AF//平面MBD.
( http: / / www.21cnjy.com )
3.如图, 长方体ABCD-A1B1C1D1中, P, Q, R, 分别为BC, CD, CC1的中点.
(1)判断直线B1D1与平面PQR的位置关系; 平行
(2)判断平面AB1D1与平面PQR的位置关系; 平行
(3)判断平面PQR与平面DD1B1B的位置关系. 相交
4.下列命题中正确的个数为 B
(1)如果一条直线与一平面平行,那么这条直线与平面内的任意一条直线平行;
(2)如果一条直线与一平面相交,那么这条直线与平面内的无数条直线垂直;
(3)过平面外一点有且只有一条直线与平面平行;
(4)一条直线上有两点到一个平面的距离相等,则这条直线平行于这个平面.
A.1 B.2 C.3 D.4
5.已知AB、BC、CD是不在同一平面内的三条线段,E、F、G分别是AB、BC、CD的中点,求证:平面EFG和AC平行,也和BD平行.
证明:如图,连结AC、B D、EG、EF、GF,
在△ABC中,E、F分别是AB、BC的中点
AC//EF, ,
,
六、课堂小结,
①线面平行、面面平行的定义和判定定理
②三种语言的转化
③划归思想面面、线面、线线三者间的转换
七、作业布置 P34 A组 4,5,6 ,B组3
一、教材的地位与作用
平行关系的判定是在线与线、线与面、面与面 ( http: / / www.21cnjy.com )的知识结构中起着承上启下的作用,也是今后学习共面向量的基础。在此之前,学生已学习了空间两直线的位置关系,这为过渡到本节的学习起着铺垫作用。本节的主要内容有直线和平面的三种位置关系和直线与平面平行的判定两部分。平行关系是全章的主要内容之一,而直线与平面平行的判定是平行关系的初步。因此,在立体几何中,占据重要的地位。
二、教学目标
1.知识与技能: (1)理解并掌握线面平行、面面平行的判定定理及其应用;
(2)能将数学三种语言(自然语言、图形语言、符号语言)相互转化
2. 过程与方法:借助已有知识,通过观 ( http: / / www.21cnjy.com )察模型,抽象概况出线面平行、面面平行的定义,类比线面平探索面面平行的判定定理, 培养学生的划归思想、空间想象力和抽象概括能力
3.情感态度与价值观:在学习过程中,使学生获得积极的情感,培养数学学习的兴趣
三、教学重难点
教学重点:线面平行和平面与平面平行的定义和判定定理
教学难点:线面平行和平面与平面平行的判定定理的推导和应用
四、教法学法:
采用直观类比法、探究发现法、观察实验法等教 ( http: / / www.21cnjy.com )学方法,教师通过创设问题探究,引导学生通过直观感知,操作确认逐步发现知识的形成过程,使教学活动真正建立在学生自主活动和探究的基础上,着力培养学生的抽象概括能力和空间想象能力.
五、教学过程
(一)温故知新:
复习回顾
1. 空间直线与平面的位置关系有_3_种:
2. 空间平面与平面的位置关系有_2_种:
一、直线与平面平行的判定
1.问题提出: 如何判定一条直线和一个平面平行
( http: / / www.21cnjy.com )
2.抽象概括:
直线与平面平行的判定定理
如果平面外一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行.
3.应 用:
例1.求证:空间四边形相邻两边的中点的连线,平行于经过另外两边的平面.
已知:空间四边形ABCD中,E、F分别是AB、AD的中点. 求证:EF//平面BCD.
证明:连结BD,
例2. 如图所示, 空间四 ( http: / / www.21cnjy.com )边形ABCD中, E, F, G, H分别是AB, BC, CD, AD的中点. 试指出图中满足线面平行位置关系的所有情况.
( http: / / www.21cnjy.com )
二、平面与平面平行的判定
1.问题提出: 如何判定一个平面和另一个平面平行
( http: / / www.21cnjy.com )
1.空间线面有哪些位置关系呢?
2.学习过几种判断直线与平面平行的方法
(1)定义法;
(2)直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则 该直线与此平面平行.
设计意图:回顾探究与线面平行的转化思想方法,自然语言的描述、图形语言画法和符号语言的表述,为类比学习面面平行做铺垫
2.探究发现,得出定理
观察:长方体和三棱柱两个教具模型
1.上表面两直线与底面的关系,符号语言如何表述?
2上表面和下表面是否有交点?
抽象概况出面面平行的定义:①,②记作: ③ 图形如何画?
设计意图:由线面平行定义直观映射出面面平行的定义,从直观过渡到抽象推理.
探究活动1:①将长方体和三棱柱平移和旋转,上下地面是否还平行?
②将长方体底面的边和三棱柱底面顶点抬起是否上表面平行桌面?
探究活动2: 1、平面内有一条直线与平面平行, 则平面,平行吗?
2、平面内有两条直线与平面平行,平面,平行吗?
3、平面内有无数条直线与平面平行,平面,平行吗?
设计意图: 由知识回顾到问题提出很自然 ( http: / / www.21cnjy.com )。以疑导思,使学生在问题带动下进行更加主动的思维活动,经历从实际背景中抽象出数学模型、从现实的生活空间中抽象出几何图形和几何问题的过程,注重探索空间图形性质的过程。 由现实生活抽象到数学知识 以问题的形式让学生小组探讨,激发学生的探索欲望,营造一个让学生主动观察、思考、讨论的氛围。
学生在实例的探究中,思考并寻找平面与平面平行的判定条件是什么,从而概括提炼出平面与平面平行的判定定理。
2.抽象概括:平面与平面平行的判定定理:
如果一个平面内有两条相交直线都平行于另一个平面, 那么这两个平面平行.
3.应 用:
总结思路,体会思想 :面面平行--线面平行--线线平行 。
设计意图:通过实际问题探究、讨论,思辨,及时巩固定理,运用定理,培养学生的识图能力与逻辑推理能力,同时体会转化思想。
三、反馈练习
1. 过直线外一点与该直线平行的平面有__无数__个. 过平面外一点与该平面平行的直线有_无数___条.
2.平行四边形ABCD和平行四边形CDEF有一公共边CD, 它们不在同一平面内, M为FC的中点. 求证: AF//平面MBD.
( http: / / www.21cnjy.com )
3.如图, 长方体ABCD-A1B1C1D1中, P, Q, R, 分别为BC, CD, CC1的中点.
(1)判断直线B1D1与平面PQR的位置关系; 平行
(2)判断平面AB1D1与平面PQR的位置关系; 平行
(3)判断平面PQR与平面DD1B1B的位置关系. 相交
4.下列命题中正确的个数为 B
(1)如果一条直线与一平面平行,那么这条直线与平面内的任意一条直线平行;
(2)如果一条直线与一平面相交,那么这条直线与平面内的无数条直线垂直;
(3)过平面外一点有且只有一条直线与平面平行;
(4)一条直线上有两点到一个平面的距离相等,则这条直线平行于这个平面.
A.1 B.2 C.3 D.4
5.已知AB、BC、CD是不在同一平面内的三条线段,E、F、G分别是AB、BC、CD的中点,求证:平面EFG和AC平行,也和BD平行.
证明:如图,连结AC、B D、EG、EF、GF,
在△ABC中,E、F分别是AB、BC的中点
AC//EF, ,
,
六、课堂小结,
①线面平行、面面平行的定义和判定定理
②三种语言的转化
③划归思想面面、线面、线线三者间的转换
七、作业布置 P34 A组 4,5,6 ,B组3
