2016北师大版数学必修二教学设计:1.5.2平行关系的性质
文档属性
| 名称 | 2016北师大版数学必修二教学设计:1.5.2平行关系的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-24 17:35:03 | ||
图片预览

文档简介
5.2平行关系的性质教案
江西省南昌市铁路第一中学 章建荣
一、教材的地位与作用
在本节课之前,学生已经学行关系的判 ( http: / / www.21cnjy.com )定,对于平行关系的性质的学习,不仅是对前面学行关系的判定进行延伸拓展,更是为接下来学习垂直关系的性质、提供了方法依据,起着承前启后的作用。同时,从本章节整体知识体系来说,立体几何初步的学习对培养学生的辩证唯物主义观点、空间想象能力和逻辑思维能力等方面,都具有重要的作用。
二、教学目标
1、知识与技能目标:理解平行关系的性质,掌握平行关系的性质的应用;
2、过程与方法目标:通过对平行关系的性质定理的探究和运用过程,进一步培养学生的辩证唯物主义观点、空间想象能力和逻辑思维能力;
3、情感态度与价值观目标:让学生亲身经历数学定理的形成过程,体验探索的乐趣,增强学生学习数学的兴趣。
三、教学重难点
教学重点:对平行关系性质的理解、概括和应用。
教学难点:对平行关系的性质的理解、概括,掌握平行之间的转化,灵活运用平行关系的性质 解决实际问题
四、教法学法
通过观察、讨论、分析、探索等 ( http: / / www.21cnjy.com )步骤,让学生自己“设问、尝试、归纳、总结、运用”,重视学生的主动参与,注重信息反馈。这样,一方面培养学生抽象思维能力和空间想向能力.
五、教学过程
温故知新:
线面平行判定定理:
面面平行判定定理
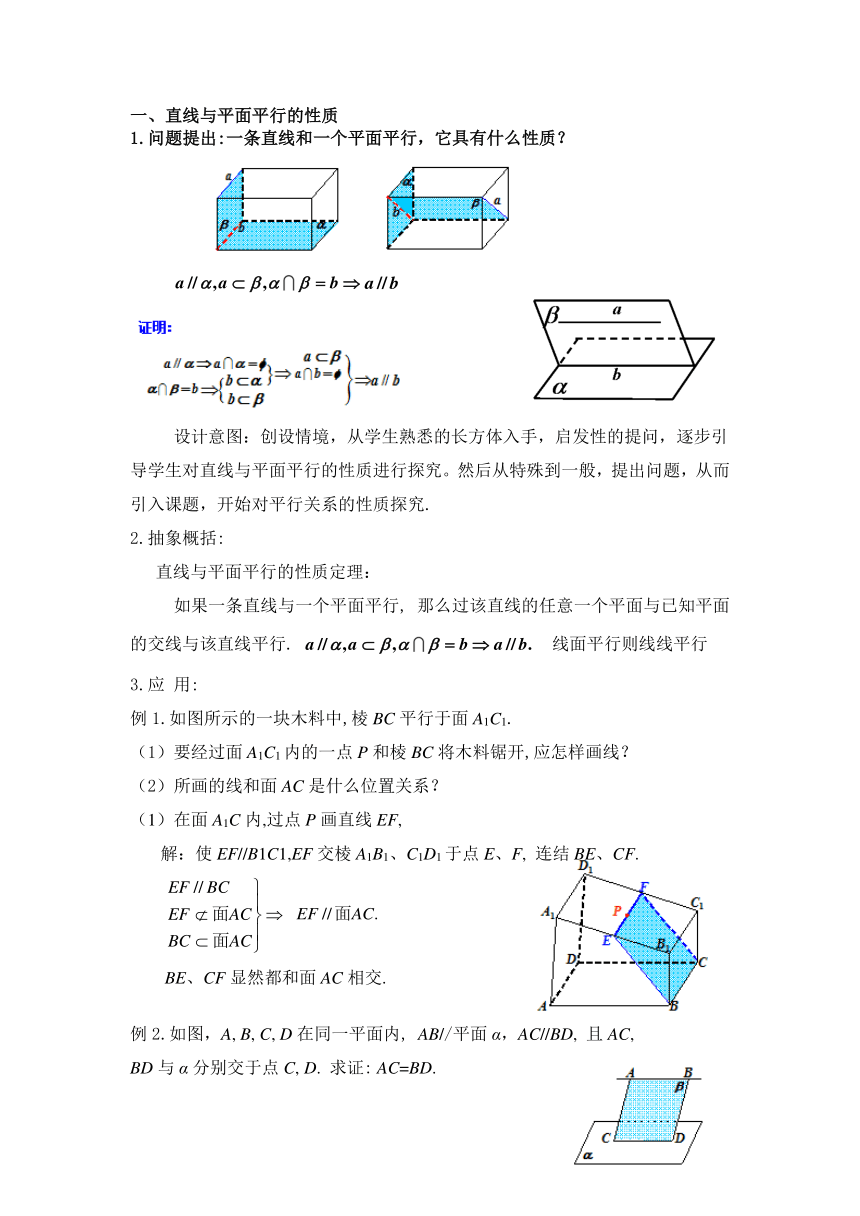
一、直线与平面平行的性质
1.问题提出:一条直线和一个平面平行,它具有什么性质?
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
设计意图:创设情境,从学生熟悉的长方体入手 ( http: / / www.21cnjy.com ),启发性的提问,逐步引导学生对直线与平面平行的性质进行探究。然后从特殊到一般,提出问题,从而引入课题,开始对平行关系的性质探究.
2.抽象概括:
直线与平面平行的性质定理:
如果一条直线与一个平面平行, 那么过该直线的任意一个平面与已知平面的交线与该直线平行. 线面平行则线线平行
3.应 用:
例1.如图所示的一块木料中,棱BC平行于面A1C1.
(1)要经过面A1C1内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC是什么位置关系?
(1)在面A1C内,过点P画直线EF,
解:使EF//B1C1,EF交棱A1B1、C1D1于点E、F, 连结BE、CF.
BE、CF显然都和面AC相交.
例2.如图,A, B, C, D在同一平面内, AB//平面α,AC//BD, 且AC,
BD与α分别交于点C, D. 求证: AC=BD.
证明:连接CD, A, B, C, D在同一平面内,
设该平面为β. 则α∩β=CD. AB//平面α
AB//CD,AC//BD 四边形ABCD是平行四边形 AC=BD
二、两个平面平行的性质
1.问题提出:两个平面平行,它具有什么性质?
2.抽象概括:
平面与平面平行的性质定理: 如果两个平行平面同时和第三个平面相交, 那么它们
的交线平行.
(面面平行证线线平行)
3.应 用:
例3.如图, 直线a和b分别交 于点A、B、C和点D、E、F.
求证:
证明:连接AF,交平面点G.
平面ADF∩α=AD
平面ADF∩β=GE
,
平面ACF∩β=BG,平面ACF∩γ=CF
设计意图: 让学生更形象深刻的体会定理的内涵,了解定理的应用。讲解时注意在黑板上把解题步骤完整的板书出来,让学生体明证明的严谨性和规范性
思考:若DE=6, EF=2, BC=3. 则AB=___9_____.
三、反馈练习
1.如果直线a//α, 直线b, 那么a与b一定平行吗?为什么?
2.如果直线a//直线 b , 且a//α , 那么b与α的位置关系是( D )
A. 相交 B. b//a C. D. b//a 或
3.已知两条直线m, n及平面α, 判断下面四个命题是否正确:
(1)若m//α, n//α, 则m//n; 错
(2)若m//α, m//n, 则n//α; 错
(3)若m//α, 则m平行α内所有直线; 错
(4)若m平行于α内无数条直线, 则m//α . 错
4.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( D )
A. 平行 B. 相交 C. 在平面内 D. 平行或在平面内
5.如果三个平面把空间分成4个部分,那么这个平面有怎样的位置关系?如果3个平面把空间分成6个部分,那么这3个平面有怎样的位置关系?
六、课堂小结
1.直线与平面平行的性质定理 2.平面与平面平行的性质定理
在方法层面上,引导学生回顾,定理的条件与结论,进一步加深学生对定理的理解,突出教学重点,方便学生记忆。
七.作业布置P34 A组 6,7 B组 3
江西省南昌市铁路第一中学 章建荣
一、教材的地位与作用
在本节课之前,学生已经学行关系的判 ( http: / / www.21cnjy.com )定,对于平行关系的性质的学习,不仅是对前面学行关系的判定进行延伸拓展,更是为接下来学习垂直关系的性质、提供了方法依据,起着承前启后的作用。同时,从本章节整体知识体系来说,立体几何初步的学习对培养学生的辩证唯物主义观点、空间想象能力和逻辑思维能力等方面,都具有重要的作用。
二、教学目标
1、知识与技能目标:理解平行关系的性质,掌握平行关系的性质的应用;
2、过程与方法目标:通过对平行关系的性质定理的探究和运用过程,进一步培养学生的辩证唯物主义观点、空间想象能力和逻辑思维能力;
3、情感态度与价值观目标:让学生亲身经历数学定理的形成过程,体验探索的乐趣,增强学生学习数学的兴趣。
三、教学重难点
教学重点:对平行关系性质的理解、概括和应用。
教学难点:对平行关系的性质的理解、概括,掌握平行之间的转化,灵活运用平行关系的性质 解决实际问题
四、教法学法
通过观察、讨论、分析、探索等 ( http: / / www.21cnjy.com )步骤,让学生自己“设问、尝试、归纳、总结、运用”,重视学生的主动参与,注重信息反馈。这样,一方面培养学生抽象思维能力和空间想向能力.
五、教学过程
温故知新:
线面平行判定定理:
面面平行判定定理
一、直线与平面平行的性质
1.问题提出:一条直线和一个平面平行,它具有什么性质?
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
设计意图:创设情境,从学生熟悉的长方体入手 ( http: / / www.21cnjy.com ),启发性的提问,逐步引导学生对直线与平面平行的性质进行探究。然后从特殊到一般,提出问题,从而引入课题,开始对平行关系的性质探究.
2.抽象概括:
直线与平面平行的性质定理:
如果一条直线与一个平面平行, 那么过该直线的任意一个平面与已知平面的交线与该直线平行. 线面平行则线线平行
3.应 用:
例1.如图所示的一块木料中,棱BC平行于面A1C1.
(1)要经过面A1C1内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC是什么位置关系?
(1)在面A1C内,过点P画直线EF,
解:使EF//B1C1,EF交棱A1B1、C1D1于点E、F, 连结BE、CF.
BE、CF显然都和面AC相交.
例2.如图,A, B, C, D在同一平面内, AB//平面α,AC//BD, 且AC,
BD与α分别交于点C, D. 求证: AC=BD.
证明:连接CD, A, B, C, D在同一平面内,
设该平面为β. 则α∩β=CD. AB//平面α
AB//CD,AC//BD 四边形ABCD是平行四边形 AC=BD
二、两个平面平行的性质
1.问题提出:两个平面平行,它具有什么性质?
2.抽象概括:
平面与平面平行的性质定理: 如果两个平行平面同时和第三个平面相交, 那么它们
的交线平行.
(面面平行证线线平行)
3.应 用:
例3.如图, 直线a和b分别交 于点A、B、C和点D、E、F.
求证:
证明:连接AF,交平面点G.
平面ADF∩α=AD
平面ADF∩β=GE
,
平面ACF∩β=BG,平面ACF∩γ=CF
设计意图: 让学生更形象深刻的体会定理的内涵,了解定理的应用。讲解时注意在黑板上把解题步骤完整的板书出来,让学生体明证明的严谨性和规范性
思考:若DE=6, EF=2, BC=3. 则AB=___9_____.
三、反馈练习
1.如果直线a//α, 直线b, 那么a与b一定平行吗?为什么?
2.如果直线a//直线 b , 且a//α , 那么b与α的位置关系是( D )
A. 相交 B. b//a C. D. b//a 或
3.已知两条直线m, n及平面α, 判断下面四个命题是否正确:
(1)若m//α, n//α, 则m//n; 错
(2)若m//α, m//n, 则n//α; 错
(3)若m//α, 则m平行α内所有直线; 错
(4)若m平行于α内无数条直线, 则m//α . 错
4.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( D )
A. 平行 B. 相交 C. 在平面内 D. 平行或在平面内
5.如果三个平面把空间分成4个部分,那么这个平面有怎样的位置关系?如果3个平面把空间分成6个部分,那么这3个平面有怎样的位置关系?
六、课堂小结
1.直线与平面平行的性质定理 2.平面与平面平行的性质定理
在方法层面上,引导学生回顾,定理的条件与结论,进一步加深学生对定理的理解,突出教学重点,方便学生记忆。
七.作业布置P34 A组 6,7 B组 3
