1.4解直角三角形(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
1.4解直角三角形
一、单选题
1.在中,,, ,则的长是( )
A.3 B.4 C.5 D.6
2.如图,在Rt△ABC中,∠ACB=900,CD⊥AB于点D,BC=3,AC=4,tan∠BCD的值为( )
A. ; B. ; C. ; D. ;
3.在中,,,,尺规作图方式如图所示,( )
A. B. C. D.
4.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,相交于点O,则( )
A. B. C. D.
5.如图,将绕点A按顺时针方向旋转一定角度得到,点B的对应点D恰好落在边上.若,则的长为( )
A.0.5 B.1.5 C. D.1
二、填空题
6.如图,在平面直角坐标系中,等边三角形OAB的边OB在x轴上,点A在第一象限,,点C在线段OA上,且.将沿射线OA的方向平移至的位置,此时点的坐标是 .
7.如图,边长为1的正方形绕点A逆时针旋转得到正方形,则图中阴影部分的面积为 .
8.在△ABC中,AB=12 , AC=13,cos∠B= , 则BC边长为 .
9.如图,正六边形螺帽的边长是,那么这个扳手的开口的值是 .
10.在中,,,,则的度数为 .
11.如图,的正方形网格中,A、B、C、D为格点,连接、相交于点E,则的值是 .
三、计算题
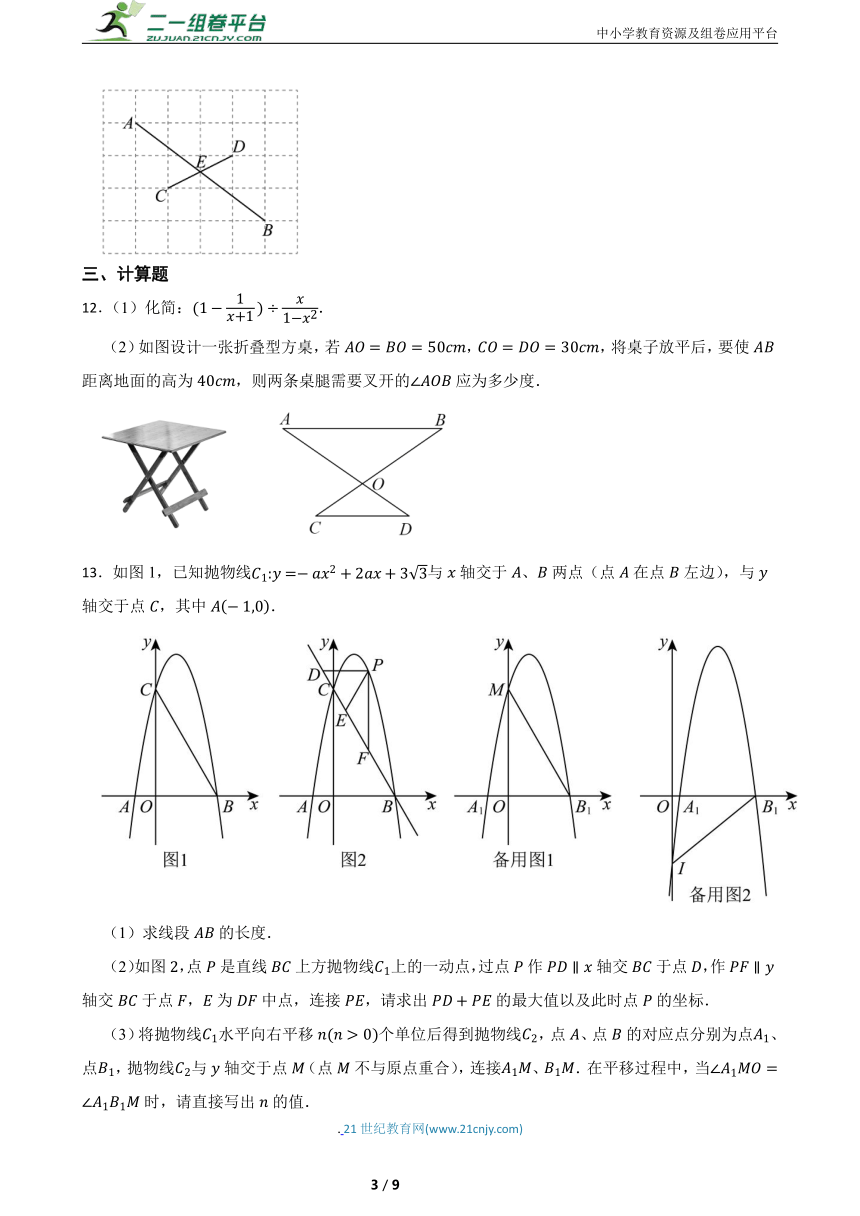
12.(1)化简:.
(2)如图设计一张折叠型方桌,若,,将桌子放平后,要使距离地面的高为,则两条桌腿需要叉开的应为多少度.
13.如图1,已知抛物线与轴交于、两点(点在点左边),与轴交于点,其中.
(1)求线段的长度.
(2)如图,点是直线上方抛物线上的一动点,过点作轴交于点,作轴交于点,为中点,连接,请求出的最大值以及此时点的坐标.
(3)将抛物线水平向右平移个单位后得到抛物线,点、点的对应点分别为点、点,抛物线与轴交于点(点不与原点重合),连接、.在平移过程中,当时,请直接写出的值.
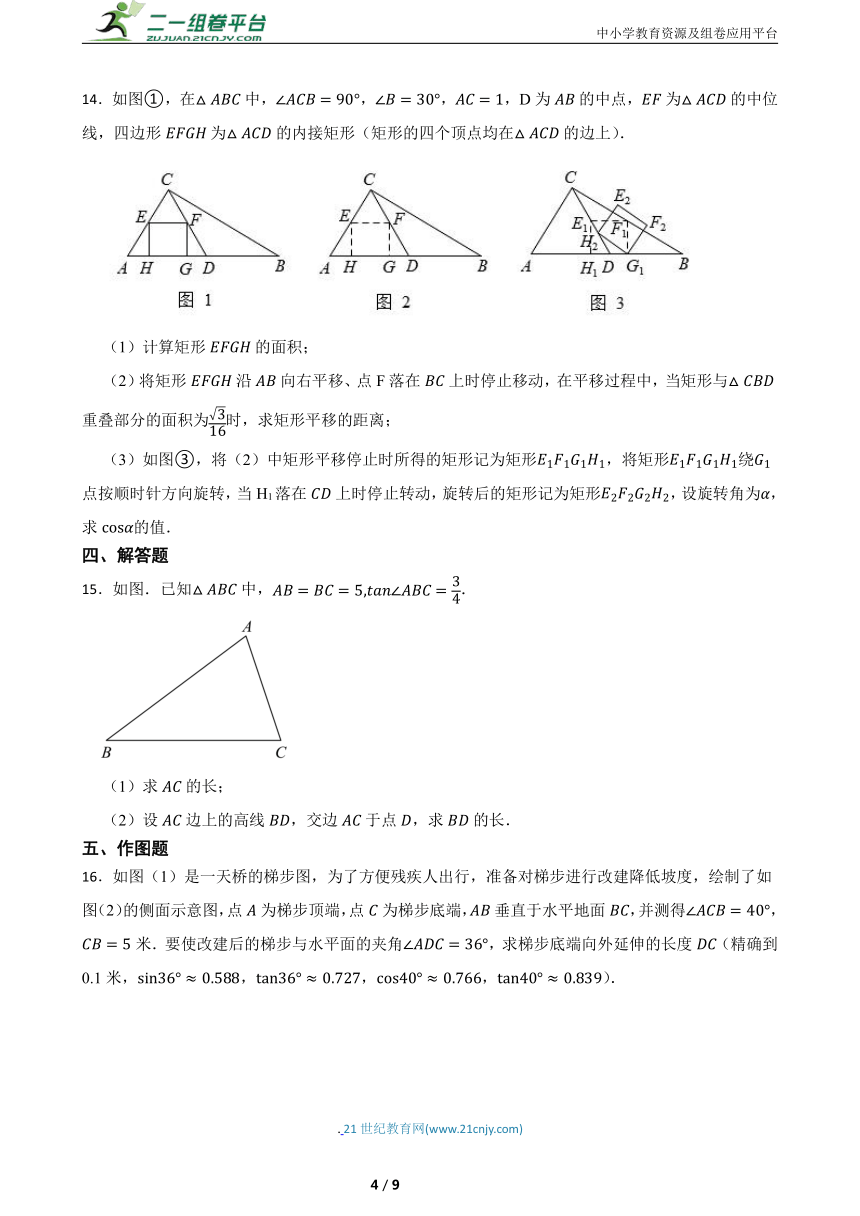
14.如图①,在中,,,,D为的中点,为的中位线,四边形为的内接矩形(矩形的四个顶点均在的边上).
(1)计算矩形的面积;
(2)将矩形沿向右平移、点F落在上时停止移动,在平移过程中,当矩形与重叠部分的面积为时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形,将矩形绕点按顺时针方向旋转,当H1落在上时停止转动,旋转后的矩形记为矩形,设旋转角为,求的值.
四、解答题
15.如图.已知中,.
(1)求的长;
(2)设边上的高线,交边于点,求的长.
五、作图题
16.如图(1)是一天桥的梯步图,为了方便残疾人出行,准备对梯步进行改建降低坡度,绘制了如图(2)的侧面示意图,点为梯步顶端,点为梯步底端,垂直于水平地面,并测得,米.要使改建后的梯步与水平面的夹角,求梯步底端向外延伸的长度(精确到0.1米,,,,).
六、综合题
17.如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
18.如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC.
(1)求证:AC=BD
(2)若sin∠C= ,BC=12,求AD的长.
19.如图①,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,∠CGD=42°.将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示。
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
(1)∠CBH的大小为 度.
(2)点H、B的读数分别为4、13.4,求BC的长.(结果精确到0.01)
答案解析部分
1.【答案】A
【知识点】勾股定理;解直角三角形
2.【答案】A
【知识点】解直角三角形
3.【答案】D
【知识点】等腰三角形的判定与性质;解直角三角形;尺规作图-垂线
4.【答案】D
【知识点】勾股定理;解直角三角形
5.【答案】D
【知识点】解直角三角形
6.【答案】(,)
【知识点】平移的性质;解直角三角形
7.【答案】
【知识点】直角三角形全等的判定-HL;正方形的性质;解直角三角形;旋转的性质
8.【答案】或
【知识点】解直角三角形
9.【答案】
【知识点】解直角三角形
10.【答案】
【知识点】求特殊角的三角函数值;解直角三角形
11.【答案】
【知识点】勾股定理;平行四边形的判定与性质;解直角三角形
12.【答案】(1);(2)
【知识点】分式的加减法;等腰三角形的性质;解直角三角形
13.【答案】(1);
(2);;
(3),.
【知识点】解直角三角形
14.【答案】(1)
(2)
(3)
【知识点】解直角三角形;三角形的中位线定理;直角三角形斜边上的中线
15.【答案】(1)
(2)
【知识点】勾股定理;解直角三角形
16.【答案】0.8米
【知识点】解直角三角形
17.【答案】(1)解:延长AC交ON于点E,如图,
∵AC⊥ON,
∴∠OEC=90°,
在Rt△OEC中,
∵∠O=25°,
∴∠OCE=65°,
∴∠ACB=∠OCE=65°,
∴∠ACD=90°﹣∠ACB=25°
(2)解:∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,
在Rt△ABC中,∵cos∠ACB= ,
∴BC=AC cos65°=5×0.42=2.1,
∴AD=BC=2.1
【知识点】解直角三角形
18.【答案】(1)证明:∵AD是BC上的高,∴AD⊥BC,∴∠ADB=90°,∠ADC=90°.在Rt△ABD和Rt△ADC中,∵tanB= ,cos∠DAC= ,tanB=cos∠DAC,∴ = ,∴AC=BD
(2)解:在Rt△ADC中,sinC= ,故可设AD=12k,AC=13k,∴CD= =5k,∵BC=BD+CD,AC=BD,∴BC=13k+5k=18k.由已知BC=12,∴18k=12,∴k= ,∴AD=12k=12× =8.
【知识点】解直角三角形
19.【答案】(1)42
(2)解:由图得,BH=13.4-4=9.4.
在Rt△BCH中,∠C=90°,∠CBH=42°,
∵ , ∴ . ∴BC的长约为6.96
【知识点】平移的性质;解直角三角形
.
21世纪教育网(www.21cnjy.com)
5 / 9
1.4解直角三角形
一、单选题
1.在中,,, ,则的长是( )
A.3 B.4 C.5 D.6
2.如图,在Rt△ABC中,∠ACB=900,CD⊥AB于点D,BC=3,AC=4,tan∠BCD的值为( )
A. ; B. ; C. ; D. ;
3.在中,,,,尺规作图方式如图所示,( )
A. B. C. D.
4.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,相交于点O,则( )
A. B. C. D.
5.如图,将绕点A按顺时针方向旋转一定角度得到,点B的对应点D恰好落在边上.若,则的长为( )
A.0.5 B.1.5 C. D.1
二、填空题
6.如图,在平面直角坐标系中,等边三角形OAB的边OB在x轴上,点A在第一象限,,点C在线段OA上,且.将沿射线OA的方向平移至的位置,此时点的坐标是 .
7.如图,边长为1的正方形绕点A逆时针旋转得到正方形,则图中阴影部分的面积为 .
8.在△ABC中,AB=12 , AC=13,cos∠B= , 则BC边长为 .
9.如图,正六边形螺帽的边长是,那么这个扳手的开口的值是 .
10.在中,,,,则的度数为 .
11.如图,的正方形网格中,A、B、C、D为格点,连接、相交于点E,则的值是 .
三、计算题
12.(1)化简:.
(2)如图设计一张折叠型方桌,若,,将桌子放平后,要使距离地面的高为,则两条桌腿需要叉开的应为多少度.
13.如图1,已知抛物线与轴交于、两点(点在点左边),与轴交于点,其中.
(1)求线段的长度.
(2)如图,点是直线上方抛物线上的一动点,过点作轴交于点,作轴交于点,为中点,连接,请求出的最大值以及此时点的坐标.
(3)将抛物线水平向右平移个单位后得到抛物线,点、点的对应点分别为点、点,抛物线与轴交于点(点不与原点重合),连接、.在平移过程中,当时,请直接写出的值.
14.如图①,在中,,,,D为的中点,为的中位线,四边形为的内接矩形(矩形的四个顶点均在的边上).
(1)计算矩形的面积;
(2)将矩形沿向右平移、点F落在上时停止移动,在平移过程中,当矩形与重叠部分的面积为时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形,将矩形绕点按顺时针方向旋转,当H1落在上时停止转动,旋转后的矩形记为矩形,设旋转角为,求的值.
四、解答题
15.如图.已知中,.
(1)求的长;
(2)设边上的高线,交边于点,求的长.
五、作图题
16.如图(1)是一天桥的梯步图,为了方便残疾人出行,准备对梯步进行改建降低坡度,绘制了如图(2)的侧面示意图,点为梯步顶端,点为梯步底端,垂直于水平地面,并测得,米.要使改建后的梯步与水平面的夹角,求梯步底端向外延伸的长度(精确到0.1米,,,,).
六、综合题
17.如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
18.如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC.
(1)求证:AC=BD
(2)若sin∠C= ,BC=12,求AD的长.
19.如图①,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,∠CGD=42°.将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示。
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
(1)∠CBH的大小为 度.
(2)点H、B的读数分别为4、13.4,求BC的长.(结果精确到0.01)
答案解析部分
1.【答案】A
【知识点】勾股定理;解直角三角形
2.【答案】A
【知识点】解直角三角形
3.【答案】D
【知识点】等腰三角形的判定与性质;解直角三角形;尺规作图-垂线
4.【答案】D
【知识点】勾股定理;解直角三角形
5.【答案】D
【知识点】解直角三角形
6.【答案】(,)
【知识点】平移的性质;解直角三角形
7.【答案】
【知识点】直角三角形全等的判定-HL;正方形的性质;解直角三角形;旋转的性质
8.【答案】或
【知识点】解直角三角形
9.【答案】
【知识点】解直角三角形
10.【答案】
【知识点】求特殊角的三角函数值;解直角三角形
11.【答案】
【知识点】勾股定理;平行四边形的判定与性质;解直角三角形
12.【答案】(1);(2)
【知识点】分式的加减法;等腰三角形的性质;解直角三角形
13.【答案】(1);
(2);;
(3),.
【知识点】解直角三角形
14.【答案】(1)
(2)
(3)
【知识点】解直角三角形;三角形的中位线定理;直角三角形斜边上的中线
15.【答案】(1)
(2)
【知识点】勾股定理;解直角三角形
16.【答案】0.8米
【知识点】解直角三角形
17.【答案】(1)解:延长AC交ON于点E,如图,
∵AC⊥ON,
∴∠OEC=90°,
在Rt△OEC中,
∵∠O=25°,
∴∠OCE=65°,
∴∠ACB=∠OCE=65°,
∴∠ACD=90°﹣∠ACB=25°
(2)解:∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,
在Rt△ABC中,∵cos∠ACB= ,
∴BC=AC cos65°=5×0.42=2.1,
∴AD=BC=2.1
【知识点】解直角三角形
18.【答案】(1)证明:∵AD是BC上的高,∴AD⊥BC,∴∠ADB=90°,∠ADC=90°.在Rt△ABD和Rt△ADC中,∵tanB= ,cos∠DAC= ,tanB=cos∠DAC,∴ = ,∴AC=BD
(2)解:在Rt△ADC中,sinC= ,故可设AD=12k,AC=13k,∴CD= =5k,∵BC=BD+CD,AC=BD,∴BC=13k+5k=18k.由已知BC=12,∴18k=12,∴k= ,∴AD=12k=12× =8.
【知识点】解直角三角形
19.【答案】(1)42
(2)解:由图得,BH=13.4-4=9.4.
在Rt△BCH中,∠C=90°,∠CBH=42°,
∵ , ∴ . ∴BC的长约为6.96
【知识点】平移的性质;解直角三角形
.
21世纪教育网(www.21cnjy.com)
5 / 9
