1.5三角函数的应用(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
1.5三角函数的应用
一、单选题
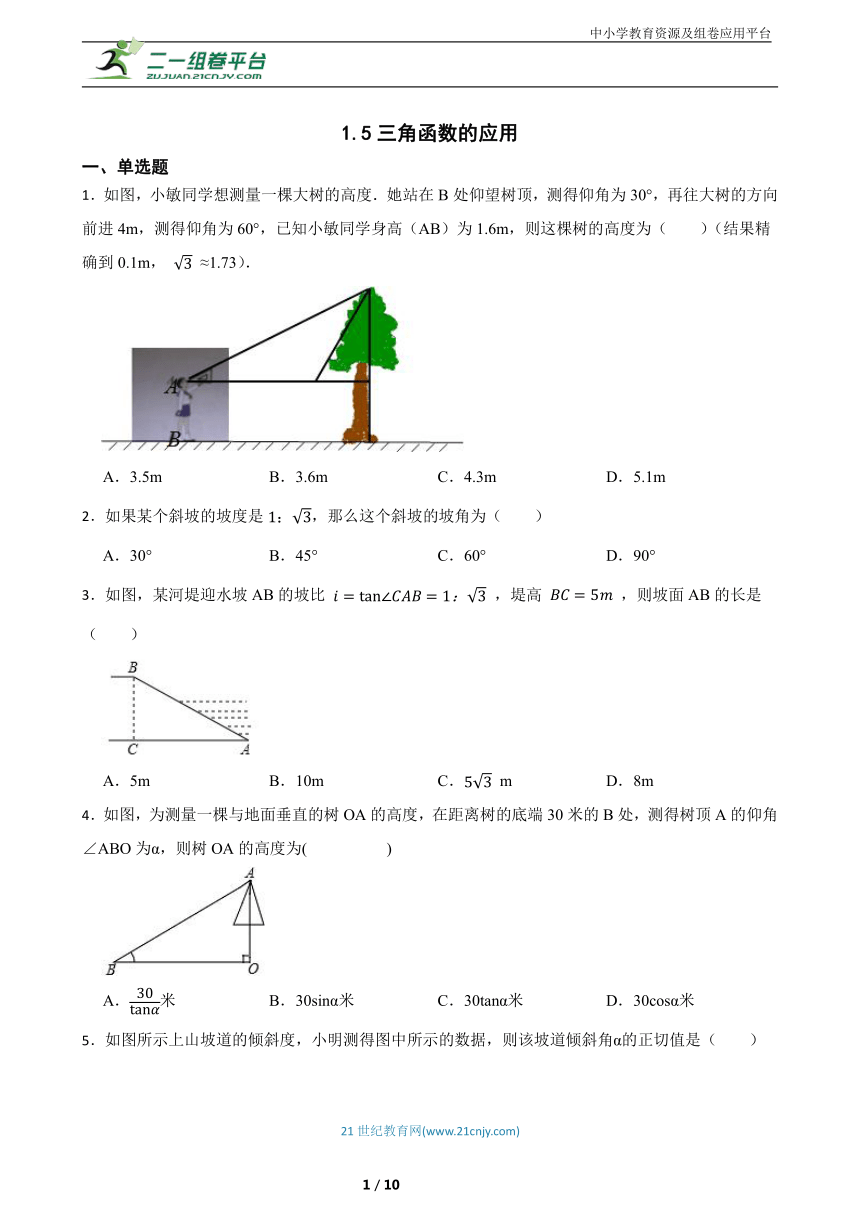
1.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m, ≈1.73).
A.3.5m B.3.6m C.4.3m D.5.1m
2.如果某个斜坡的坡度是,那么这个斜坡的坡角为( )
A.30° B.45° C.60° D.90°
3.如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )
A.5m B.10m C. m D.8m
4.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
5.如图所示上山坡道的倾斜度,小明测得图中所示的数据,则该坡道倾斜角α的正切值是( )
A. B. C. D.
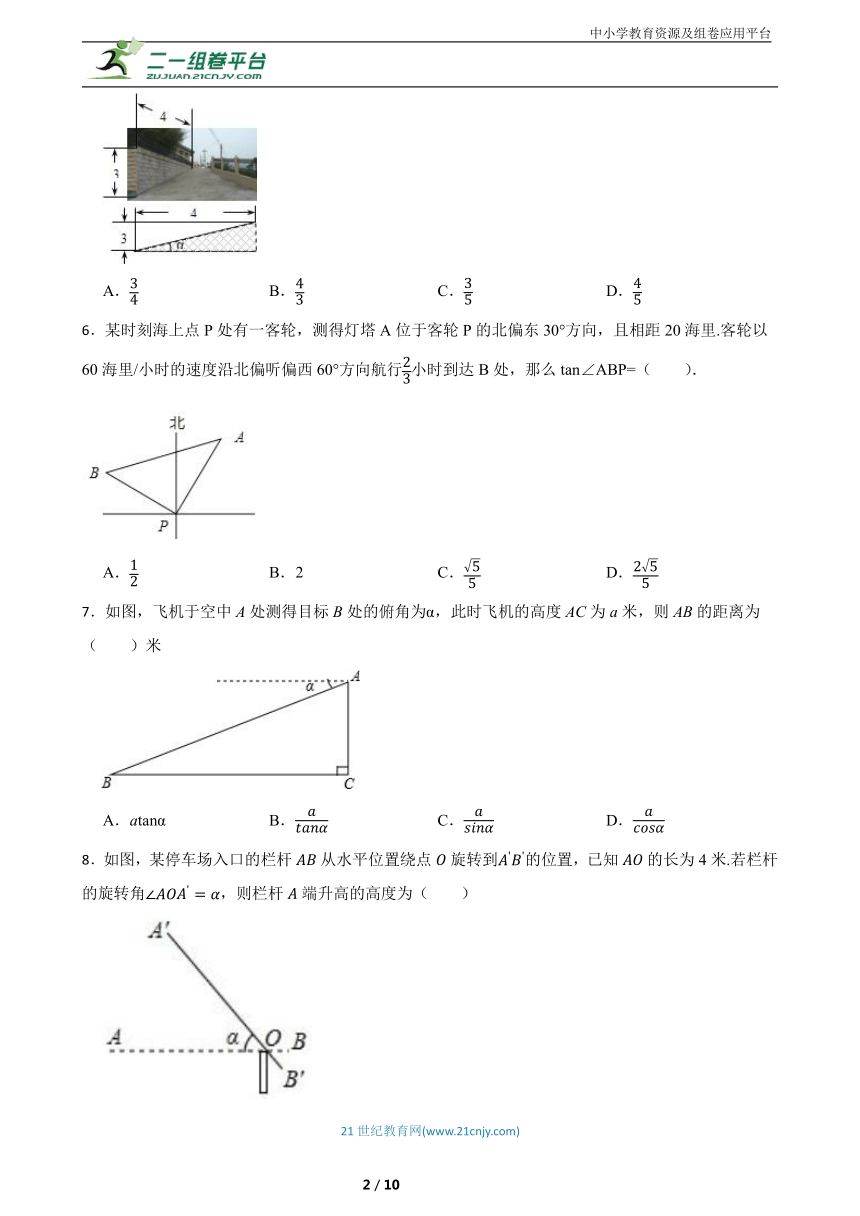
6.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏听偏西60°方向航行小时到达B处,那么tan∠ABP=( ).
A. B.2 C. D.
7.如图,飞机于空中A处测得目标B处的俯角为α,此时飞机的高度AC为a米,则AB的距离为( )米
A.atanα B. C. D.
8.如图,某停车场入口的栏杆从水平位置绕点旋转到的位置,已知的长为4米.若栏杆的旋转角,则栏杆端升高的高度为( )
A.米 B.米 C.米 D.米
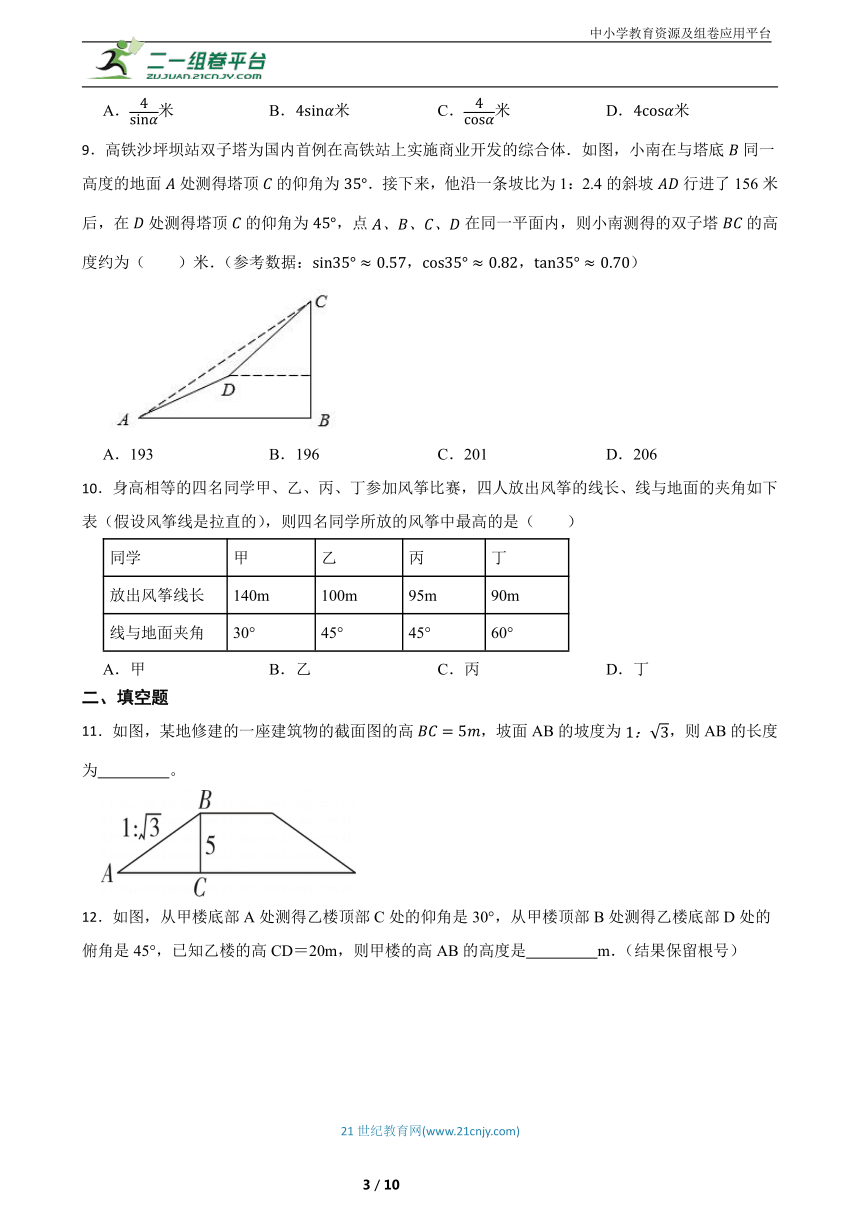
9.高铁沙坪坝站双子塔为国内首例在高铁站上实施商业开发的综合体.如图,小南在与塔底同一高度的地面处测得塔顶的仰角为.接下来,他沿一条坡比为1:2.4的斜坡行进了156米后,在处测得塔顶的仰角为,点在同一平面内,则小南测得的双子塔的高度约为( )米.(参考数据:,,)
A.193 B.196 C.201 D.206
10.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
同学 甲 乙 丙 丁
放出风筝线长 140m 100m 95m 90m
线与地面夹角 30° 45° 45° 60°
A.甲 B.乙 C.丙 D.丁
二、填空题
11.如图,某地修建的一座建筑物的截面图的高,坡面AB的坡度为,则AB的长度为 。
12.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD=20m,则甲楼的高AB的高度是 m.(结果保留根号)
13.在一个距离地面5米高的平台上测得一旗杆底部的俯角为30°,旗杆顶部的仰角为45°,则该旗杆的高度为 米.(结果保留根号)
14.计划在楼层间修建一个坡角为35°的楼梯,若楼层间高度为2.7m,为了节省成本,现要将楼梯坡角增加11°,则楼梯的斜面长度约减少 m.(用科学计算器计算,结果精确到0.01m).
15.疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.
16.衢州儿童公园有摩天轮,水上乐园等娱乐设施,其中的摩天轮半径为20米,水上乐园的最高处到地面的距离为32米;如图,当摩天轮的座舱A旋转至与水上乐园最高处高度相同时,地面某观测点P与座舱A,摩天轮圆心O恰好在同一条直线上,此时测得,则的距离为 米;此时另一座舱B位于摩天轮最低点,摩天轮旋转一周要12分钟,若摩天轮继续逆时针旋转一周,当从座舱A观测座舱B的俯角为45°时,经过了 分钟.
三、计算题
17.如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得树顶端A的仰角为30°,已知侧角仪高DC=1.4m,BC=30米,请帮助小明计算出树高AB.
18.在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37°≈,tan37°≈,sin21°≈,tan21°≈ )
19.为了更好地检测复学后学生进校时的体温情况,某小学购买了如下左图所示的带支架的红外热成像仪,该仪器能探测从仪器旁经过学生的体温,若超过就会发出警报.该仪器由三根等长的斜拉支架和一根竖直支架共同支撑上边的红外测温仪已知四根支架总长为5.5米,一根斜拉支架与竖直支架的长度比为3:2.
(1)如图1,当斜拉支架与地面的夹角为时,请计算红外测温仪距离地面的高度(连接处均忽略不计);
(2)在使用期间发现,将顶端测温仪倾斜与水平线夹角为,斜拉支架与铅垂线的夹角也是时,学生(按平均身高)走到距离点米的点处时,测温仪与学生的额头恰好在一条直线上,这样调整能使测量的温度比较准确(如图2所示),请结合题中所给数据计算学生的平均身高.(结果精确到0.1米,参考数据:,,,,,)
四、解答题
20.北斗卫星导航系统是中国自行研制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶10千米至B地,再沿北偏东方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.
(1)求的度数;
(2)求B,C两地的距离.(如果运算结果有根号,请保留根号)
21.一架无人机沿水平直线飞行进行测绘工作,在点处测得左边水平地面上某汽车的顶端点的俯角为,同一时刻测得右边某建筑物顶端点的俯角为,已知建筑物的高度米,汽车的高度米,汽车与建筑物的距离为30米,求无人机飞行的高度.(结果精确到1米,参考数据:,.
22.越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度的长.(结果精确到1米;参考数据:)
23.如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈,cos27°≈,tan27°≈,sin53°≈,cos53°≈,tan53°≈)
答案解析部分
1.【答案】D
【知识点】解直角三角形的实际应用﹣仰角俯角问题
2.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
3.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题
4.【答案】C
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
6.【答案】A
【知识点】解直角三角形的实际应用﹣方向角问题
7.【答案】C
【知识点】解直角三角形的实际应用﹣仰角俯角问题
8.【答案】B
【知识点】解直角三角形的其他实际应用
9.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
10.【答案】D
【知识点】解直角三角形的其他实际应用
11.【答案】10m
【知识点】解直角三角形的实际应用﹣坡度坡角问题
12.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】5+5
【知识点】解直角三角形的实际应用﹣仰角俯角问题
14.【答案】0.95
【知识点】解直角三角形的实际应用﹣坡度坡角问题
15.【答案】;(52 ﹣78)
【知识点】等边三角形的判定与性质;解直角三角形的其他实际应用
16.【答案】;或
【知识点】解直角三角形的实际应用﹣仰角俯角问题
17.【答案】(10+1.4)米
【知识点】勾股定理的逆定理;解直角三角形的实际应用﹣仰角俯角问题
18.【答案】古塔的高度约是39米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)2.4米;(2)1.6米
【知识点】解直角三角形的其他实际应用
20.【答案】(1)
(2)千米.
【知识点】解直角三角形的实际应用﹣方向角问题
21.【答案】无人机飞行的高度约为40米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】8米
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
23.【答案】解:如图,根据题意可得,在△ABC中,AB=99海里,∠ABC=53°,∠BAC=27°,
过点C作CD⊥AB,垂足为点D.
设BD=x海里,则AD=(99﹣x)海里,
在Rt△BCD中,tan53°=,
则tan27°=,
CD=x tan53°≈x(海里).
在Rt△ACD中,则CD=AD tan27°≈(99﹣x),
则x=(99﹣x),
解得,x=27,
即BD=27.
在Rt△BCD中,cos53°=,
则BC===45,
45÷2=22.5(海里/时),
则该可疑船只的航行速度约为22.5海里/时.
【知识点】解直角三角形的实际应用﹣方向角问题
21世纪教育网(www.21cnjy.com)
2 / 10
1.5三角函数的应用
一、单选题
1.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m, ≈1.73).
A.3.5m B.3.6m C.4.3m D.5.1m
2.如果某个斜坡的坡度是,那么这个斜坡的坡角为( )
A.30° B.45° C.60° D.90°
3.如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )
A.5m B.10m C. m D.8m
4.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
5.如图所示上山坡道的倾斜度,小明测得图中所示的数据,则该坡道倾斜角α的正切值是( )
A. B. C. D.
6.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏听偏西60°方向航行小时到达B处,那么tan∠ABP=( ).
A. B.2 C. D.
7.如图,飞机于空中A处测得目标B处的俯角为α,此时飞机的高度AC为a米,则AB的距离为( )米
A.atanα B. C. D.
8.如图,某停车场入口的栏杆从水平位置绕点旋转到的位置,已知的长为4米.若栏杆的旋转角,则栏杆端升高的高度为( )
A.米 B.米 C.米 D.米
9.高铁沙坪坝站双子塔为国内首例在高铁站上实施商业开发的综合体.如图,小南在与塔底同一高度的地面处测得塔顶的仰角为.接下来,他沿一条坡比为1:2.4的斜坡行进了156米后,在处测得塔顶的仰角为,点在同一平面内,则小南测得的双子塔的高度约为( )米.(参考数据:,,)
A.193 B.196 C.201 D.206
10.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
同学 甲 乙 丙 丁
放出风筝线长 140m 100m 95m 90m
线与地面夹角 30° 45° 45° 60°
A.甲 B.乙 C.丙 D.丁
二、填空题
11.如图,某地修建的一座建筑物的截面图的高,坡面AB的坡度为,则AB的长度为 。
12.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD=20m,则甲楼的高AB的高度是 m.(结果保留根号)
13.在一个距离地面5米高的平台上测得一旗杆底部的俯角为30°,旗杆顶部的仰角为45°,则该旗杆的高度为 米.(结果保留根号)
14.计划在楼层间修建一个坡角为35°的楼梯,若楼层间高度为2.7m,为了节省成本,现要将楼梯坡角增加11°,则楼梯的斜面长度约减少 m.(用科学计算器计算,结果精确到0.01m).
15.疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.
16.衢州儿童公园有摩天轮,水上乐园等娱乐设施,其中的摩天轮半径为20米,水上乐园的最高处到地面的距离为32米;如图,当摩天轮的座舱A旋转至与水上乐园最高处高度相同时,地面某观测点P与座舱A,摩天轮圆心O恰好在同一条直线上,此时测得,则的距离为 米;此时另一座舱B位于摩天轮最低点,摩天轮旋转一周要12分钟,若摩天轮继续逆时针旋转一周,当从座舱A观测座舱B的俯角为45°时,经过了 分钟.
三、计算题
17.如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得树顶端A的仰角为30°,已知侧角仪高DC=1.4m,BC=30米,请帮助小明计算出树高AB.
18.在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37°≈,tan37°≈,sin21°≈,tan21°≈ )
19.为了更好地检测复学后学生进校时的体温情况,某小学购买了如下左图所示的带支架的红外热成像仪,该仪器能探测从仪器旁经过学生的体温,若超过就会发出警报.该仪器由三根等长的斜拉支架和一根竖直支架共同支撑上边的红外测温仪已知四根支架总长为5.5米,一根斜拉支架与竖直支架的长度比为3:2.
(1)如图1,当斜拉支架与地面的夹角为时,请计算红外测温仪距离地面的高度(连接处均忽略不计);
(2)在使用期间发现,将顶端测温仪倾斜与水平线夹角为,斜拉支架与铅垂线的夹角也是时,学生(按平均身高)走到距离点米的点处时,测温仪与学生的额头恰好在一条直线上,这样调整能使测量的温度比较准确(如图2所示),请结合题中所给数据计算学生的平均身高.(结果精确到0.1米,参考数据:,,,,,)
四、解答题
20.北斗卫星导航系统是中国自行研制的全球卫星导航系统,其由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶10千米至B地,再沿北偏东方向行驶一段距离到达风景区C,小敏发现风景区C在A地的北偏东方向.
(1)求的度数;
(2)求B,C两地的距离.(如果运算结果有根号,请保留根号)
21.一架无人机沿水平直线飞行进行测绘工作,在点处测得左边水平地面上某汽车的顶端点的俯角为,同一时刻测得右边某建筑物顶端点的俯角为,已知建筑物的高度米,汽车的高度米,汽车与建筑物的距离为30米,求无人机飞行的高度.(结果精确到1米,参考数据:,.
22.越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度的长.(结果精确到1米;参考数据:)
23.如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈,cos27°≈,tan27°≈,sin53°≈,cos53°≈,tan53°≈)
答案解析部分
1.【答案】D
【知识点】解直角三角形的实际应用﹣仰角俯角问题
2.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
3.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题
4.【答案】C
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
6.【答案】A
【知识点】解直角三角形的实际应用﹣方向角问题
7.【答案】C
【知识点】解直角三角形的实际应用﹣仰角俯角问题
8.【答案】B
【知识点】解直角三角形的其他实际应用
9.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
10.【答案】D
【知识点】解直角三角形的其他实际应用
11.【答案】10m
【知识点】解直角三角形的实际应用﹣坡度坡角问题
12.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】5+5
【知识点】解直角三角形的实际应用﹣仰角俯角问题
14.【答案】0.95
【知识点】解直角三角形的实际应用﹣坡度坡角问题
15.【答案】;(52 ﹣78)
【知识点】等边三角形的判定与性质;解直角三角形的其他实际应用
16.【答案】;或
【知识点】解直角三角形的实际应用﹣仰角俯角问题
17.【答案】(10+1.4)米
【知识点】勾股定理的逆定理;解直角三角形的实际应用﹣仰角俯角问题
18.【答案】古塔的高度约是39米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)2.4米;(2)1.6米
【知识点】解直角三角形的其他实际应用
20.【答案】(1)
(2)千米.
【知识点】解直角三角形的实际应用﹣方向角问题
21.【答案】无人机飞行的高度约为40米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】8米
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
23.【答案】解:如图,根据题意可得,在△ABC中,AB=99海里,∠ABC=53°,∠BAC=27°,
过点C作CD⊥AB,垂足为点D.
设BD=x海里,则AD=(99﹣x)海里,
在Rt△BCD中,tan53°=,
则tan27°=,
CD=x tan53°≈x(海里).
在Rt△ACD中,则CD=AD tan27°≈(99﹣x),
则x=(99﹣x),
解得,x=27,
即BD=27.
在Rt△BCD中,cos53°=,
则BC===45,
45÷2=22.5(海里/时),
则该可疑船只的航行速度约为22.5海里/时.
【知识点】解直角三角形的实际应用﹣方向角问题
21世纪教育网(www.21cnjy.com)
2 / 10
