第一章 直角三角形的边角关系综合题(含答案)
文档属性
| 名称 | 第一章 直角三角形的边角关系综合题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 871.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 20:55:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章直角三角形的边角关系综合题
一、单选题
1.tan45°的值为( )
A. B.1 C. D.
2.如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米.
A.asin40° B.acos40° C.atan40° D.
3.如图,在△ABC中,∠C=90°,AB=3,BC=2,则cosB的值是( )
A. B. C. D.
4.如图,在 中, , , ,则 的值为( )
A. B. C. D.
5.下列实数中,是有理数的是( )
A. B.cos45° C. D.
6.如图,在山坡上种树,坡度i=1:2,AB=5m,则相邻两树的水平距离AC为( )
A.5m B. m C.2 m D.10m
7.如图为北京冬奥会“雪飞天”滑雪大跳台赛道.若点D与点A的水平距离米,水平赛道米,赛道的坡角均为,则点A的高为(
A.米 B.米
C.米 D.米
8.对于锐角α,sinα的值不可能为( )
A. B. C. D.2
9.等腰三角形的底角为15,腰长a为,则此等腰三角形的底长为( )
A. B. C. D. a
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,如图2,翻折∠ABC,∠ADC,使两个角的顶点重合于对角线BD上一点P,EF,GH分别是折痕.设BE=x(0<x<2),给出下列判断:
①当x=1时,DP的长为;
②EF+GH的值随x的变化而变化;
③六边形AEFCHG面积的最大值是;
④六边形AEFCHG周长的值不变.
其中正确的是( )
A.①② B.①④ C.②③④ D.①③④
二、填空题
11.在Rt△ABC中,∠C=90,sinA= ,则sinB= .
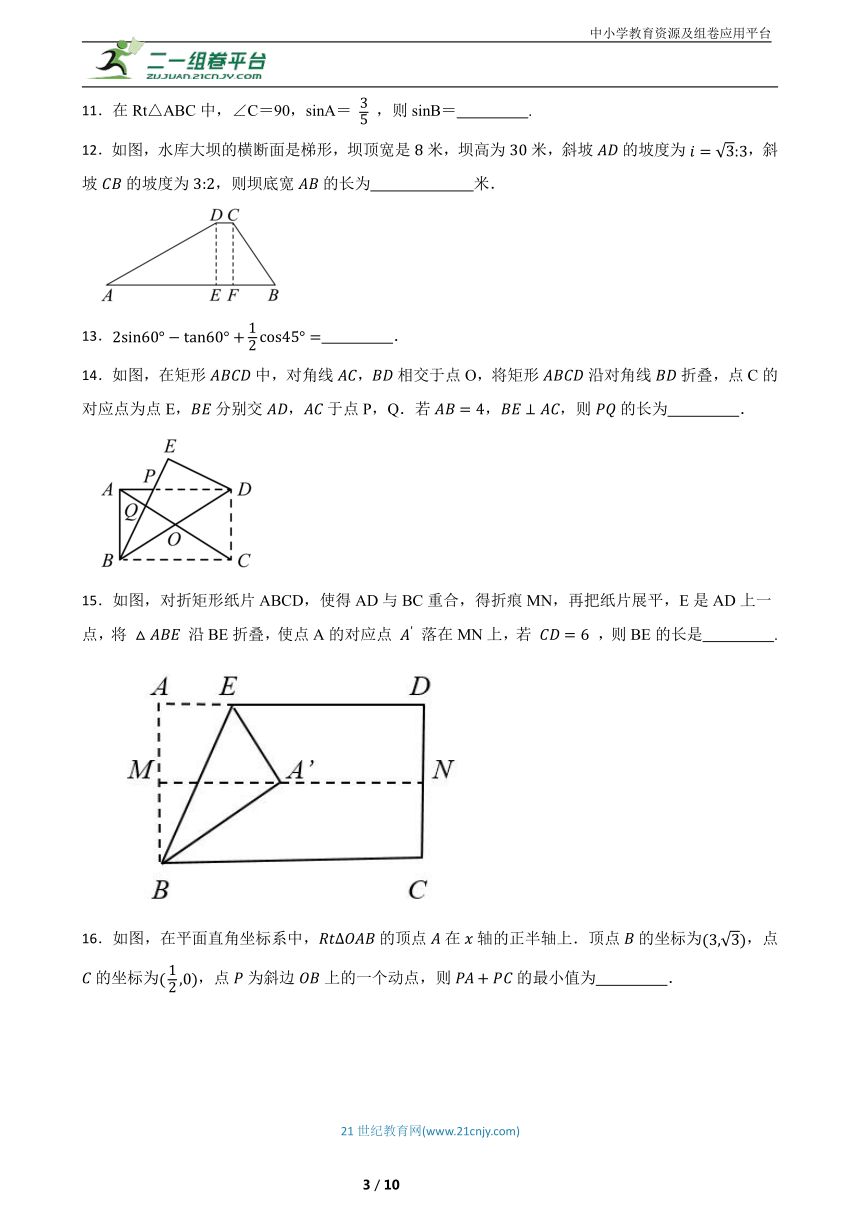
12.如图,水库大坝的横断面是梯形,坝顶宽是米,坝高为米,斜坡的坡度为,斜坡的坡度为,则坝底宽的长为 米.
13. .
14.如图,在矩形中,对角线,相交于点O,将矩形沿对角线折叠,点C的对应点为点E,分别交,于点P,Q.若,,则的长为 .
15.如图,对折矩形纸片ABCD,使得AD与BC重合,得折痕MN,再把纸片展平,E是AD上一点,将 沿BE折叠,使点A的对应点 落在MN上,若 ,则BE的长是 .
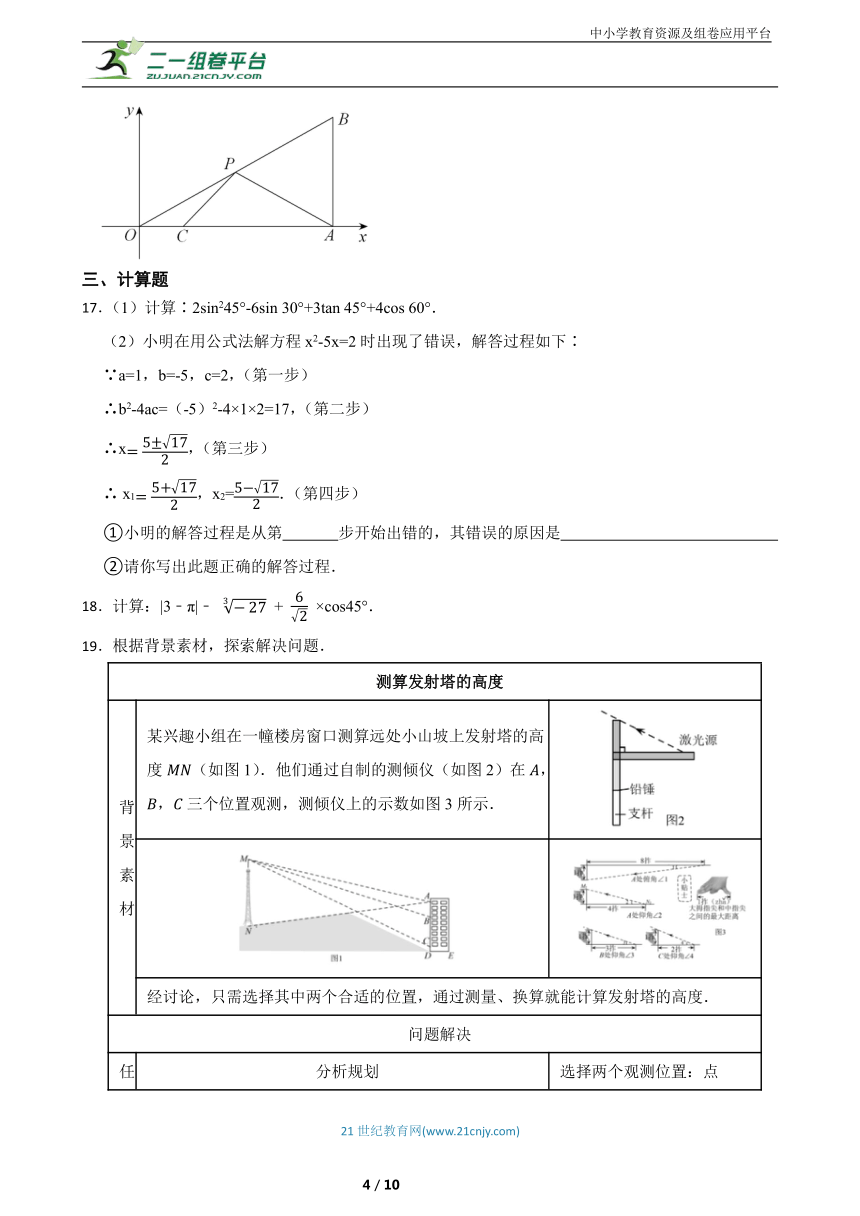
16.如图,在平面直角坐标系中,的顶点在轴的正半轴上.顶点的坐标为,点的坐标为,点为斜边上的一个动点,则的最小值为 .
三、计算题
17.(1)计算∶2sin245°-6sin 30°+3tan 45°+4cos 60°.
(2)小明在用公式法解方程x2-5x=2时出现了错误,解答过程如下∶
∵a=1,b=-5,c=2,(第一步)
∴b2-4ac=(-5)2-4×1×2=17,(第二步)
∴x,(第三步)
∴ x1,x2=.(第四步)
①小明的解答过程是从第 步开始出错的,其错误的原因是
②请你写出此题正确的解答过程.
18.计算:|3﹣π|﹣ + ×cos45°.
19.根据背景素材,探索解决问题.
测算发射塔的高度
背 景 素 材 某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度(如图1).他们通过自制的测倾仪(如图2)在,,三个位置观测,测倾仪上的示数如图3所示.
经讨论,只需选择其中两个合适的位置,通过测量、换算就能计算发射塔的高度.
问题解决
任务1 分析规划 选择两个观测位置:点_________和点_________
获取数据 写出所选位置观测角的正切值,并量出观测点之间的图上距离.
任务2 推理计算 计算发射塔的图上高度.
任务3 换算高度 楼房实际宽度为米,请通过测量换算发射塔的实际高度.
注:测量时,以答题纸上的图上距离为准,并精确到1.
四、解答题
20.“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼的高度,测量方案如图:先将无人机垂直上升至距水平地面225m的P点,测得奇楼顶端A的俯角为,再将无人机沿水平方向飞行200m到达点Q,测得奇楼底端B的俯角为,求奇楼的高度.(结果精确到1m,参考数据:,,)
21.计算:
22.计算:|﹣3|+ tan30°﹣﹣(2008﹣π)0.
23.如图,在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.求A,B间的距离.( ≈1.73, ≈1.4,结果保留一位小数).
24.已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB= ,求BC的长.
25.小亮乘车在一段正东方向的高速公路上行驶时,看到远处与高速公路平行的国道上有一座桥,他在A处发现桥的起点B在A点的北偏东的方向上,并测得米,当车前进200米到达D处时,测得桥的终点C在D点的北偏东的方向上,求桥的长度(精确到米,参考数据:,,,).
答案解析部分
1.【答案】B
【知识点】求特殊角的三角函数值
2.【答案】C
【知识点】解直角三角形
3.【答案】C
【知识点】锐角三角函数的定义
4.【答案】C
【知识点】锐角三角函数的定义
5.【答案】D
【知识点】实数的概念与分类;求特殊角的三角函数值
6.【答案】C
【知识点】解直角三角形的实际应用﹣坡度坡角问题
7.【答案】A
【知识点】解直角三角形的其他实际应用
8.【答案】D
【知识点】锐角三角函数的定义
9.【答案】D
【知识点】等腰三角形的性质;锐角三角函数的定义;求特殊角的三角函数值
10.【答案】D
【知识点】菱形的性质;解直角三角形
11.【答案】
【知识点】锐角三角函数的定义
12.【答案】
【知识点】解直角三角形的实际应用﹣坡度坡角问题
13.【答案】
【知识点】求特殊角的三角函数值
14.【答案】
【知识点】矩形的性质;解直角三角形
15.【答案】
【知识点】矩形的性质;翻折变换(折叠问题);解直角三角形
16.【答案】
【知识点】勾股定理;坐标与图形变化﹣对称;解直角三角形
17.【答案】(1)3;(2)①一,原方程没有化成一般形式;②x1,x2
【知识点】公式法解一元二次方程;求特殊角的三角函数值
18.【答案】解:原式=π﹣3+3+3
=π+3
【知识点】实数的运算;求特殊角的三角函数值
19.【答案】规划一:[任务 1]选择点和点;,,,测得图上;[任务 2];[任务 3]发射塔的实际高度为米;规划二:[任务 1]选择点和点.[任务 2];[任务 3]发射塔的实际高度为米;
【知识点】解直角三角形的其他实际应用
20.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】解:原式=1+ -1+(-3)-3×
=(-3)+ -
=-3
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值;实数的绝对值
22.【答案】解:原式=3+ -2-1=3+1﹣2﹣1=1.
(注:只写后两步也给满分.)
【知识点】相反数及有理数的相反数;实数的运算;零指数幂;求特殊角的三角函数值
23.【答案】解:过点C作CD⊥AB,垂足为点D,
则∠ACD=60°,∠BCD=45°,如图所示.
在Rt△BCD中,sin∠BCD= ,cos∠BCD= ,
∴BD=BC sin∠BCD=20×3× ≈42,CD=BC cos∠BCD=20×3× ≈42;
在Rt△ACD中,tan∠ACD= ,
∴AD=CD tan∠ACD=42× ≈72.2.
∴AB=AD+BD=72.2+42=114.2.
∴A,B间的距离约为114.2海里.
【知识点】解直角三角形的实际应用﹣方向角问题
24.【答案】解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示,
∵AC平分∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AD=DC.∵AD=5,AB=DC,
∴AD=DC=AB=5.
过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∴
在Rt△AEB中,
设AE=3x,则BE=4x.
∵AB=5,
∴
∴x=1(负值舍去).
∴AE=3,BE=4.同理可得FC=4.
∵AE⊥BC,DF⊥BC,
∴AE∥DF.
∵AD∥BC,
∴四边形AEFD是平行四边形。
∴EF=AD=5.
∴BC=13.
【知识点】平行四边形的判定与性质;解直角三角形
25.【答案】米
【知识点】解直角三角形的实际应用﹣方向角问题
21世纪教育网(www.21cnjy.com)
2 / 10
第一章直角三角形的边角关系综合题
一、单选题
1.tan45°的值为( )
A. B.1 C. D.
2.如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米.
A.asin40° B.acos40° C.atan40° D.
3.如图,在△ABC中,∠C=90°,AB=3,BC=2,则cosB的值是( )
A. B. C. D.
4.如图,在 中, , , ,则 的值为( )
A. B. C. D.
5.下列实数中,是有理数的是( )
A. B.cos45° C. D.
6.如图,在山坡上种树,坡度i=1:2,AB=5m,则相邻两树的水平距离AC为( )
A.5m B. m C.2 m D.10m
7.如图为北京冬奥会“雪飞天”滑雪大跳台赛道.若点D与点A的水平距离米,水平赛道米,赛道的坡角均为,则点A的高为(
A.米 B.米
C.米 D.米
8.对于锐角α,sinα的值不可能为( )
A. B. C. D.2
9.等腰三角形的底角为15,腰长a为,则此等腰三角形的底长为( )
A. B. C. D. a
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,如图2,翻折∠ABC,∠ADC,使两个角的顶点重合于对角线BD上一点P,EF,GH分别是折痕.设BE=x(0<x<2),给出下列判断:
①当x=1时,DP的长为;
②EF+GH的值随x的变化而变化;
③六边形AEFCHG面积的最大值是;
④六边形AEFCHG周长的值不变.
其中正确的是( )
A.①② B.①④ C.②③④ D.①③④
二、填空题
11.在Rt△ABC中,∠C=90,sinA= ,则sinB= .
12.如图,水库大坝的横断面是梯形,坝顶宽是米,坝高为米,斜坡的坡度为,斜坡的坡度为,则坝底宽的长为 米.
13. .
14.如图,在矩形中,对角线,相交于点O,将矩形沿对角线折叠,点C的对应点为点E,分别交,于点P,Q.若,,则的长为 .
15.如图,对折矩形纸片ABCD,使得AD与BC重合,得折痕MN,再把纸片展平,E是AD上一点,将 沿BE折叠,使点A的对应点 落在MN上,若 ,则BE的长是 .
16.如图,在平面直角坐标系中,的顶点在轴的正半轴上.顶点的坐标为,点的坐标为,点为斜边上的一个动点,则的最小值为 .
三、计算题
17.(1)计算∶2sin245°-6sin 30°+3tan 45°+4cos 60°.
(2)小明在用公式法解方程x2-5x=2时出现了错误,解答过程如下∶
∵a=1,b=-5,c=2,(第一步)
∴b2-4ac=(-5)2-4×1×2=17,(第二步)
∴x,(第三步)
∴ x1,x2=.(第四步)
①小明的解答过程是从第 步开始出错的,其错误的原因是
②请你写出此题正确的解答过程.
18.计算:|3﹣π|﹣ + ×cos45°.
19.根据背景素材,探索解决问题.
测算发射塔的高度
背 景 素 材 某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度(如图1).他们通过自制的测倾仪(如图2)在,,三个位置观测,测倾仪上的示数如图3所示.
经讨论,只需选择其中两个合适的位置,通过测量、换算就能计算发射塔的高度.
问题解决
任务1 分析规划 选择两个观测位置:点_________和点_________
获取数据 写出所选位置观测角的正切值,并量出观测点之间的图上距离.
任务2 推理计算 计算发射塔的图上高度.
任务3 换算高度 楼房实际宽度为米,请通过测量换算发射塔的实际高度.
注:测量时,以答题纸上的图上距离为准,并精确到1.
四、解答题
20.“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼的高度,测量方案如图:先将无人机垂直上升至距水平地面225m的P点,测得奇楼顶端A的俯角为,再将无人机沿水平方向飞行200m到达点Q,测得奇楼底端B的俯角为,求奇楼的高度.(结果精确到1m,参考数据:,,)
21.计算:
22.计算:|﹣3|+ tan30°﹣﹣(2008﹣π)0.
23.如图,在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.求A,B间的距离.( ≈1.73, ≈1.4,结果保留一位小数).
24.已知:如图,AD∥BC,AB=CD,对角线CA平分∠BCD,AD=5,tanB= ,求BC的长.
25.小亮乘车在一段正东方向的高速公路上行驶时,看到远处与高速公路平行的国道上有一座桥,他在A处发现桥的起点B在A点的北偏东的方向上,并测得米,当车前进200米到达D处时,测得桥的终点C在D点的北偏东的方向上,求桥的长度(精确到米,参考数据:,,,).
答案解析部分
1.【答案】B
【知识点】求特殊角的三角函数值
2.【答案】C
【知识点】解直角三角形
3.【答案】C
【知识点】锐角三角函数的定义
4.【答案】C
【知识点】锐角三角函数的定义
5.【答案】D
【知识点】实数的概念与分类;求特殊角的三角函数值
6.【答案】C
【知识点】解直角三角形的实际应用﹣坡度坡角问题
7.【答案】A
【知识点】解直角三角形的其他实际应用
8.【答案】D
【知识点】锐角三角函数的定义
9.【答案】D
【知识点】等腰三角形的性质;锐角三角函数的定义;求特殊角的三角函数值
10.【答案】D
【知识点】菱形的性质;解直角三角形
11.【答案】
【知识点】锐角三角函数的定义
12.【答案】
【知识点】解直角三角形的实际应用﹣坡度坡角问题
13.【答案】
【知识点】求特殊角的三角函数值
14.【答案】
【知识点】矩形的性质;解直角三角形
15.【答案】
【知识点】矩形的性质;翻折变换(折叠问题);解直角三角形
16.【答案】
【知识点】勾股定理;坐标与图形变化﹣对称;解直角三角形
17.【答案】(1)3;(2)①一,原方程没有化成一般形式;②x1,x2
【知识点】公式法解一元二次方程;求特殊角的三角函数值
18.【答案】解:原式=π﹣3+3+3
=π+3
【知识点】实数的运算;求特殊角的三角函数值
19.【答案】规划一:[任务 1]选择点和点;,,,测得图上;[任务 2];[任务 3]发射塔的实际高度为米;规划二:[任务 1]选择点和点.[任务 2];[任务 3]发射塔的实际高度为米;
【知识点】解直角三角形的其他实际应用
20.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】解:原式=1+ -1+(-3)-3×
=(-3)+ -
=-3
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值;实数的绝对值
22.【答案】解:原式=3+ -2-1=3+1﹣2﹣1=1.
(注:只写后两步也给满分.)
【知识点】相反数及有理数的相反数;实数的运算;零指数幂;求特殊角的三角函数值
23.【答案】解:过点C作CD⊥AB,垂足为点D,
则∠ACD=60°,∠BCD=45°,如图所示.
在Rt△BCD中,sin∠BCD= ,cos∠BCD= ,
∴BD=BC sin∠BCD=20×3× ≈42,CD=BC cos∠BCD=20×3× ≈42;
在Rt△ACD中,tan∠ACD= ,
∴AD=CD tan∠ACD=42× ≈72.2.
∴AB=AD+BD=72.2+42=114.2.
∴A,B间的距离约为114.2海里.
【知识点】解直角三角形的实际应用﹣方向角问题
24.【答案】解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示,
∵AC平分∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AD=DC.∵AD=5,AB=DC,
∴AD=DC=AB=5.
过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∴
在Rt△AEB中,
设AE=3x,则BE=4x.
∵AB=5,
∴
∴x=1(负值舍去).
∴AE=3,BE=4.同理可得FC=4.
∵AE⊥BC,DF⊥BC,
∴AE∥DF.
∵AD∥BC,
∴四边形AEFD是平行四边形。
∴EF=AD=5.
∴BC=13.
【知识点】平行四边形的判定与性质;解直角三角形
25.【答案】米
【知识点】解直角三角形的实际应用﹣方向角问题
21世纪教育网(www.21cnjy.com)
2 / 10
