2.3确定二次函数的表达式(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
2.3确定二次函数的表达式
一、单选题
1.一条抛物线的开口方向与抛物线相同,顶点为,则其解析式可能为( )
A. B.
C. D.或
2.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx =5的解为( )
A. B.
C. D.
3.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为()
A.y=(x+1)2+4 B.y=(x-1)2+4
C.y=(x+1)2+2 D.y=(x-1)2+2
4.若二次函数的与的部分对应值如右表,则当时,的值为( )
… …
… 0 3 4 3 …
A. B. C.0 D.3
5.抛物线:的顶点的纵坐标为2,若,则有关该函数的最值情况,下列判断正确的是( )
甲:最大值为2,最小值为-20;乙:最大值为20,最小值为4;丙:值不确定,故无法求最值
A.只有甲正确 B.只有乙正确
C.只有丙正确 D.甲、乙、丙均不正确
二、填空题
6.已知二次函数图像与x轴相交于点,且,若二次函数经过点,则二次函数表达式为 .
7.抛物线经过点,那么这个抛物线的开口向 .
8.某一元二次方程的两个根分别为,,请写出一个经过点,两点二次函数的表达式: (写出一个符合要求的即可)
9.若某条抛物线的顶点坐标为,形状大小、开口方向与抛物线完全相同.则此抛物线的函数表达式为 .
10.已知抛物线的顶点是,形状与相同,但开口方向相反,则该抛物线解析式为.
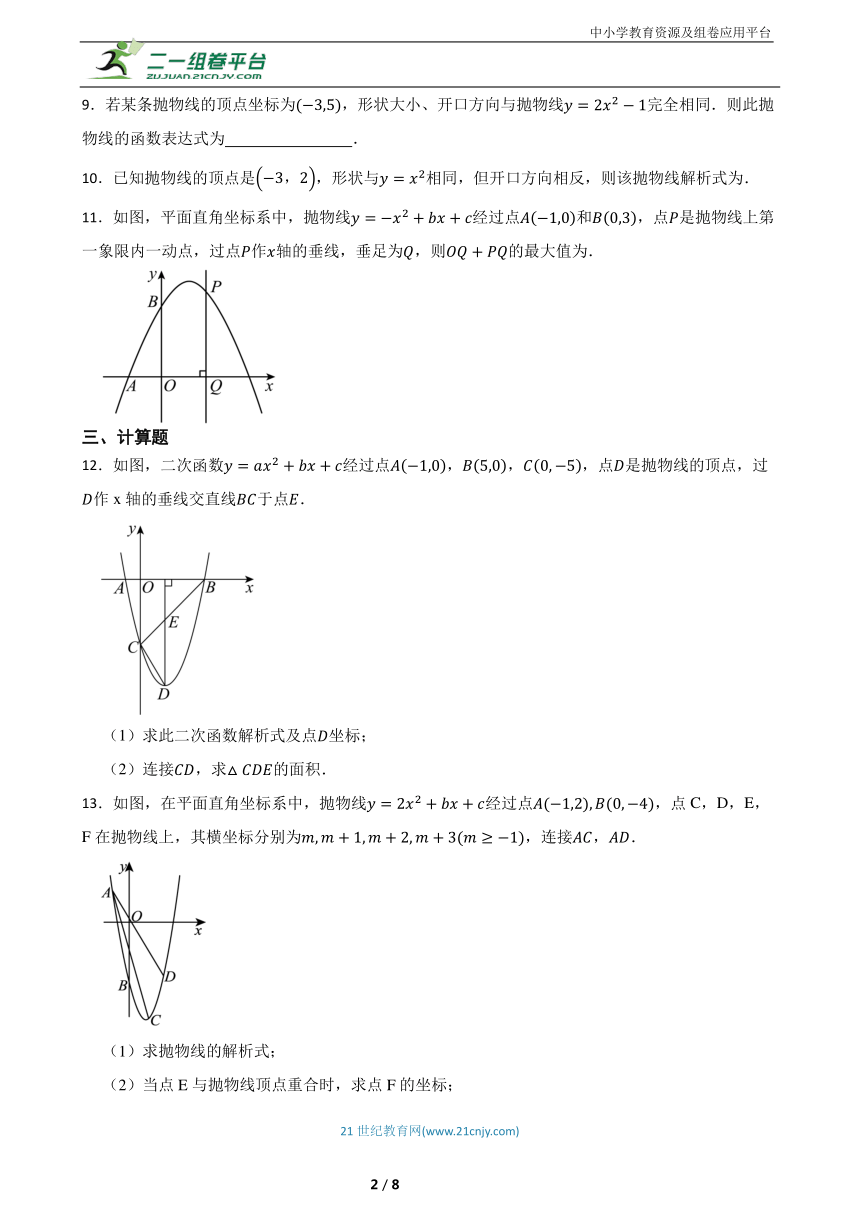
11.如图,平面直角坐标系中,抛物线经过点和,点是抛物线上第一象限内一动点,过点作轴的垂线,垂足为,则的最大值为.
三、计算题
12.如图,二次函数经过点,,,点是抛物线的顶点,过作x轴的垂线交直线于点.
(1)求此二次函数解析式及点坐标;
(2)连接,求的面积.
13.如图,在平面直角坐标系中,抛物线经过点,点C,D,E,F在抛物线上,其横坐标分别为,连接,.
(1)求抛物线的解析式;
(2)当点E与抛物线顶点重合时,求点F的坐标;
(3)当的边与y轴垂直时,求点E与点F的纵坐标;
(4)设,探索之间的关系,请直接写出结论.
14.在平面直角坐标系中,二次函数的图象与轴交于A、B两点,,与轴交于点,点是抛物线上y轴左侧的一个动点.
(1)求这个二次函数的表达式;
(2)若点关于直线的对称点恰好落在y轴上,求点的坐标.
四、解答题
15.已知抛物线.
(1)若顶点在轴上,则__________;
(2)若抛物线经过原点,求此抛物线的顶点坐标.
五、作图题
16.如图,需在公园外的一面墙上绘制几个相同的抛物线型图案.按照图中的平面直角坐标系,最左边的抛物线可以用表示,已知抛物线上B,C两点到地面的距离均为,到墙边的距离分别为,.
(1)求该抛物线的函数关系式,并求图案最高点到地面的距离.
(2)若该墙的长度为,则最多可以连续绘制几个这样的抛物线型图案?
六、综合题
17.根据以下素材,探索解决下列问题.
素材1:图①中有一个大棚苗木种植基地及其截面图,其下半部分是一个长为,宽为的矩形,其上半部分是一条抛物线,现测得,大棚顶部的最高点距离地面.以矩形长的中点为原点O,竖直方向为y轴,水平方向为x轴,建立如图②所示的平面直角坐标系,大棚顶部的最高点为P.
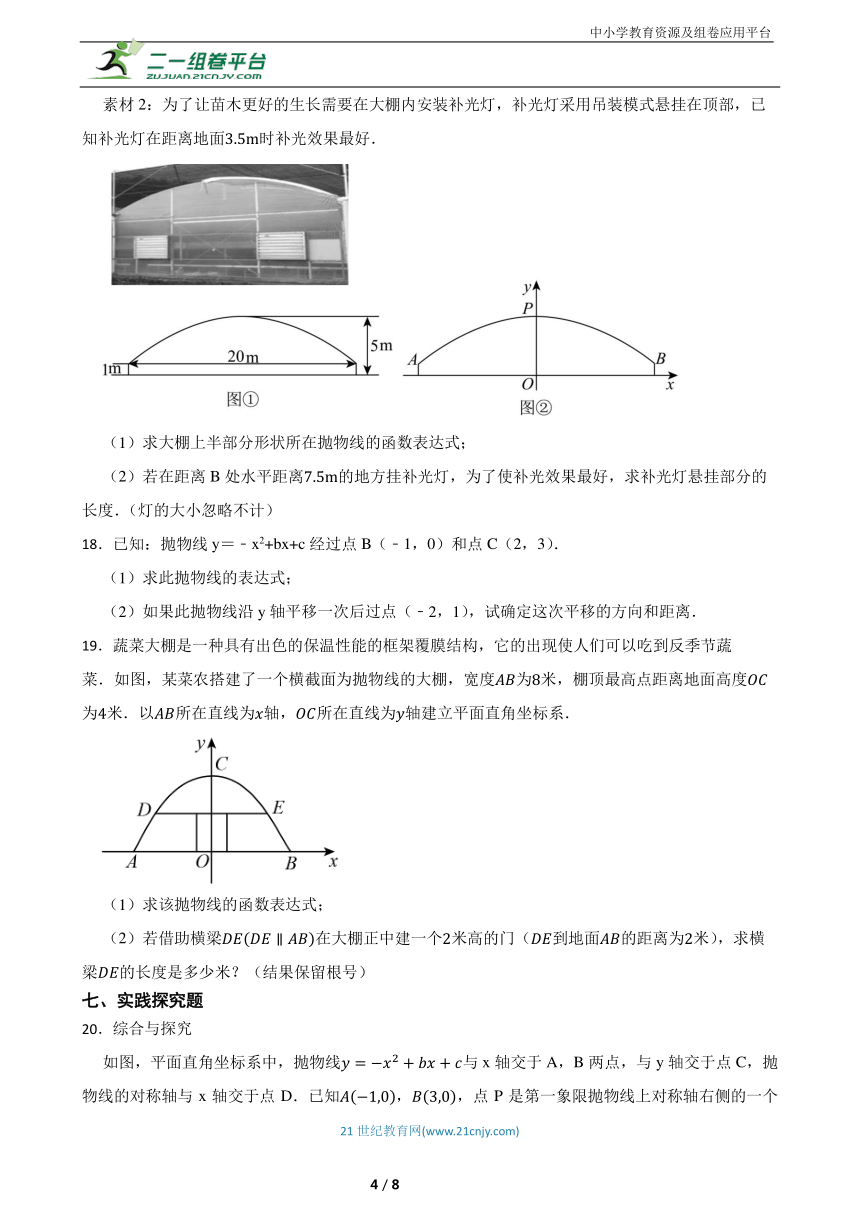
素材2:为了让苗木更好的生长需要在大棚内安装补光灯,补光灯采用吊装模式悬挂在顶部,已知补光灯在距离地面时补光效果最好.
(1)求大棚上半部分形状所在抛物线的函数表达式;
(2)若在距离B处水平距离的地方挂补光灯,为了使补光效果最好,求补光灯悬挂部分的长度.(灯的大小忽略不计)
18.已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).
(1)求此抛物线的表达式;
(2)如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.
19.蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它的出现使人们可以吃到反季节蔬菜.如图,某菜农搭建了一个横截面为抛物线的大棚,宽度为米,棚顶最高点距离地面高度为米.以所在直线为轴,所在直线为轴建立平面直角坐标系.
(1)求该抛物线的函数表达式;
(2)若借助横梁在大棚正中建一个米高的门(到地面的距离为米),求横梁的长度是多少米?(结果保留根号)
七、实践探究题
20.综合与探究
如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.已知,,点P是第一象限抛物线上对称轴右侧的一个动点,设点P的横坐标为m.
(1)求抛物线的函数表达式,并直接写出点C,D的坐标;
(2)连接,求面积的最大值.
答案解析部分
1.【答案】A
【知识点】待定系数法求二次函数解析式
2.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数与一元二次方程的综合应用
3.【答案】D
【知识点】二次函数的三种形式;配方法的应用
4.【答案】B
【知识点】待定系数法求二次函数解析式
5.【答案】D
【知识点】二次函数的最值;待定系数法求二次函数解析式
6.【答案】
【知识点】一元二次方程的根与系数的关系(韦达定理);待定系数法求二次函数解析式
7.【答案】下
【知识点】待定系数法求二次函数解析式
8.【答案】(答案不唯一)
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
9.【答案】
【知识点】待定系数法求二次函数解析式
10.【答案】
【知识点】待定系数法求二次函数解析式
11.【答案】
【知识点】待定系数法求二次函数解析式
12.【答案】(1)抛物线解析式为;
(2)的面积为6
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;二次函数-面积问题
13.【答案】(1);
(2);
(3)当的边与y轴垂直时,E的纵坐标为12,F的纵坐标为26或E的纵坐标为26,F的纵坐标为44;
(4).
【知识点】待定系数法求二次函数解析式
14.【答案】(1)
(2)
【知识点】待定系数法求二次函数解析式;勾股定理;轴对称的性质;求正切值
15.【答案】(1)
(2)
【知识点】待定系数法求二次函数解析式
16.【答案】(1)1
(2)5
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
17.【答案】(1)
(2)补光灯悬挂部分的长度应是
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
18.【答案】(1)解:把B(﹣1,0)和点C(2,3)代入y=﹣x2+bx+c
得 ,
解得 ,
所以抛物线解析式为y=﹣x2+2x﹣3;
(2)解:把x=﹣2代入y=﹣x2+2x﹣3得y=﹣4﹣4+3=﹣5,
点(﹣2,﹣5)向上平移4个单位得到点(﹣2,﹣1),
所以需将抛物线向上平移4个单位
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式
19.【答案】(1)
(2)横梁的长度是米为米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
20.【答案】(1)抛物线的函数表达式为,点C的坐标为,点D的坐标为;
(2)面积的最大值为.
【知识点】待定系数法求二次函数解析式;二次函数-面积问题
21世纪教育网(www.21cnjy.com)
2 / 8
2.3确定二次函数的表达式
一、单选题
1.一条抛物线的开口方向与抛物线相同,顶点为,则其解析式可能为( )
A. B.
C. D.或
2.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx =5的解为( )
A. B.
C. D.
3.将二次函数y=x2-2x+3化为y=(x-h)2+k的形式,结果为()
A.y=(x+1)2+4 B.y=(x-1)2+4
C.y=(x+1)2+2 D.y=(x-1)2+2
4.若二次函数的与的部分对应值如右表,则当时,的值为( )
… …
… 0 3 4 3 …
A. B. C.0 D.3
5.抛物线:的顶点的纵坐标为2,若,则有关该函数的最值情况,下列判断正确的是( )
甲:最大值为2,最小值为-20;乙:最大值为20,最小值为4;丙:值不确定,故无法求最值
A.只有甲正确 B.只有乙正确
C.只有丙正确 D.甲、乙、丙均不正确
二、填空题
6.已知二次函数图像与x轴相交于点,且,若二次函数经过点,则二次函数表达式为 .
7.抛物线经过点,那么这个抛物线的开口向 .
8.某一元二次方程的两个根分别为,,请写出一个经过点,两点二次函数的表达式: (写出一个符合要求的即可)
9.若某条抛物线的顶点坐标为,形状大小、开口方向与抛物线完全相同.则此抛物线的函数表达式为 .
10.已知抛物线的顶点是,形状与相同,但开口方向相反,则该抛物线解析式为.
11.如图,平面直角坐标系中,抛物线经过点和,点是抛物线上第一象限内一动点,过点作轴的垂线,垂足为,则的最大值为.
三、计算题
12.如图,二次函数经过点,,,点是抛物线的顶点,过作x轴的垂线交直线于点.
(1)求此二次函数解析式及点坐标;
(2)连接,求的面积.
13.如图,在平面直角坐标系中,抛物线经过点,点C,D,E,F在抛物线上,其横坐标分别为,连接,.
(1)求抛物线的解析式;
(2)当点E与抛物线顶点重合时,求点F的坐标;
(3)当的边与y轴垂直时,求点E与点F的纵坐标;
(4)设,探索之间的关系,请直接写出结论.
14.在平面直角坐标系中,二次函数的图象与轴交于A、B两点,,与轴交于点,点是抛物线上y轴左侧的一个动点.
(1)求这个二次函数的表达式;
(2)若点关于直线的对称点恰好落在y轴上,求点的坐标.
四、解答题
15.已知抛物线.
(1)若顶点在轴上,则__________;
(2)若抛物线经过原点,求此抛物线的顶点坐标.
五、作图题
16.如图,需在公园外的一面墙上绘制几个相同的抛物线型图案.按照图中的平面直角坐标系,最左边的抛物线可以用表示,已知抛物线上B,C两点到地面的距离均为,到墙边的距离分别为,.
(1)求该抛物线的函数关系式,并求图案最高点到地面的距离.
(2)若该墙的长度为,则最多可以连续绘制几个这样的抛物线型图案?
六、综合题
17.根据以下素材,探索解决下列问题.
素材1:图①中有一个大棚苗木种植基地及其截面图,其下半部分是一个长为,宽为的矩形,其上半部分是一条抛物线,现测得,大棚顶部的最高点距离地面.以矩形长的中点为原点O,竖直方向为y轴,水平方向为x轴,建立如图②所示的平面直角坐标系,大棚顶部的最高点为P.
素材2:为了让苗木更好的生长需要在大棚内安装补光灯,补光灯采用吊装模式悬挂在顶部,已知补光灯在距离地面时补光效果最好.
(1)求大棚上半部分形状所在抛物线的函数表达式;
(2)若在距离B处水平距离的地方挂补光灯,为了使补光效果最好,求补光灯悬挂部分的长度.(灯的大小忽略不计)
18.已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).
(1)求此抛物线的表达式;
(2)如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.
19.蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它的出现使人们可以吃到反季节蔬菜.如图,某菜农搭建了一个横截面为抛物线的大棚,宽度为米,棚顶最高点距离地面高度为米.以所在直线为轴,所在直线为轴建立平面直角坐标系.
(1)求该抛物线的函数表达式;
(2)若借助横梁在大棚正中建一个米高的门(到地面的距离为米),求横梁的长度是多少米?(结果保留根号)
七、实践探究题
20.综合与探究
如图,平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.已知,,点P是第一象限抛物线上对称轴右侧的一个动点,设点P的横坐标为m.
(1)求抛物线的函数表达式,并直接写出点C,D的坐标;
(2)连接,求面积的最大值.
答案解析部分
1.【答案】A
【知识点】待定系数法求二次函数解析式
2.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数与一元二次方程的综合应用
3.【答案】D
【知识点】二次函数的三种形式;配方法的应用
4.【答案】B
【知识点】待定系数法求二次函数解析式
5.【答案】D
【知识点】二次函数的最值;待定系数法求二次函数解析式
6.【答案】
【知识点】一元二次方程的根与系数的关系(韦达定理);待定系数法求二次函数解析式
7.【答案】下
【知识点】待定系数法求二次函数解析式
8.【答案】(答案不唯一)
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
9.【答案】
【知识点】待定系数法求二次函数解析式
10.【答案】
【知识点】待定系数法求二次函数解析式
11.【答案】
【知识点】待定系数法求二次函数解析式
12.【答案】(1)抛物线解析式为;
(2)的面积为6
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;二次函数-面积问题
13.【答案】(1);
(2);
(3)当的边与y轴垂直时,E的纵坐标为12,F的纵坐标为26或E的纵坐标为26,F的纵坐标为44;
(4).
【知识点】待定系数法求二次函数解析式
14.【答案】(1)
(2)
【知识点】待定系数法求二次函数解析式;勾股定理;轴对称的性质;求正切值
15.【答案】(1)
(2)
【知识点】待定系数法求二次函数解析式
16.【答案】(1)1
(2)5
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
17.【答案】(1)
(2)补光灯悬挂部分的长度应是
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
18.【答案】(1)解:把B(﹣1,0)和点C(2,3)代入y=﹣x2+bx+c
得 ,
解得 ,
所以抛物线解析式为y=﹣x2+2x﹣3;
(2)解:把x=﹣2代入y=﹣x2+2x﹣3得y=﹣4﹣4+3=﹣5,
点(﹣2,﹣5)向上平移4个单位得到点(﹣2,﹣1),
所以需将抛物线向上平移4个单位
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式
19.【答案】(1)
(2)横梁的长度是米为米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
20.【答案】(1)抛物线的函数表达式为,点C的坐标为,点D的坐标为;
(2)面积的最大值为.
【知识点】待定系数法求二次函数解析式;二次函数-面积问题
21世纪教育网(www.21cnjy.com)
2 / 8
