2.4二次函数的应用(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
2.41二次函数的应用
一、单选题
1.如图是抛物线型拱桥,当拱顶离水面时,水面宽;如果水面下降,则水面宽度增加( )
A. B. C. D.
2.中条山隧道位于山西省运城市盐湖区,这一隧道的建设开创了全省普通公路特长隧道工程建设的先河,也是全国单洞里程最长的隧道工程.如图1是中条山隧道,其截面近似为抛物线型,如图2为截面示意图,线段表示水平的路面,以O为坐标原点所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.经测量,抛物线的顶点P到的距离为,则抛物线的函数表达式为( )
A. B.
C. D.
3.如图,一边靠学校院墙,其它三边用 40 米长的篱笆围成一个矩形花圃,设矩形 ABCD 的边 AB=x 米,面积为 S 平方米,则下面关系式正确的是( )
A. B.
C. D.
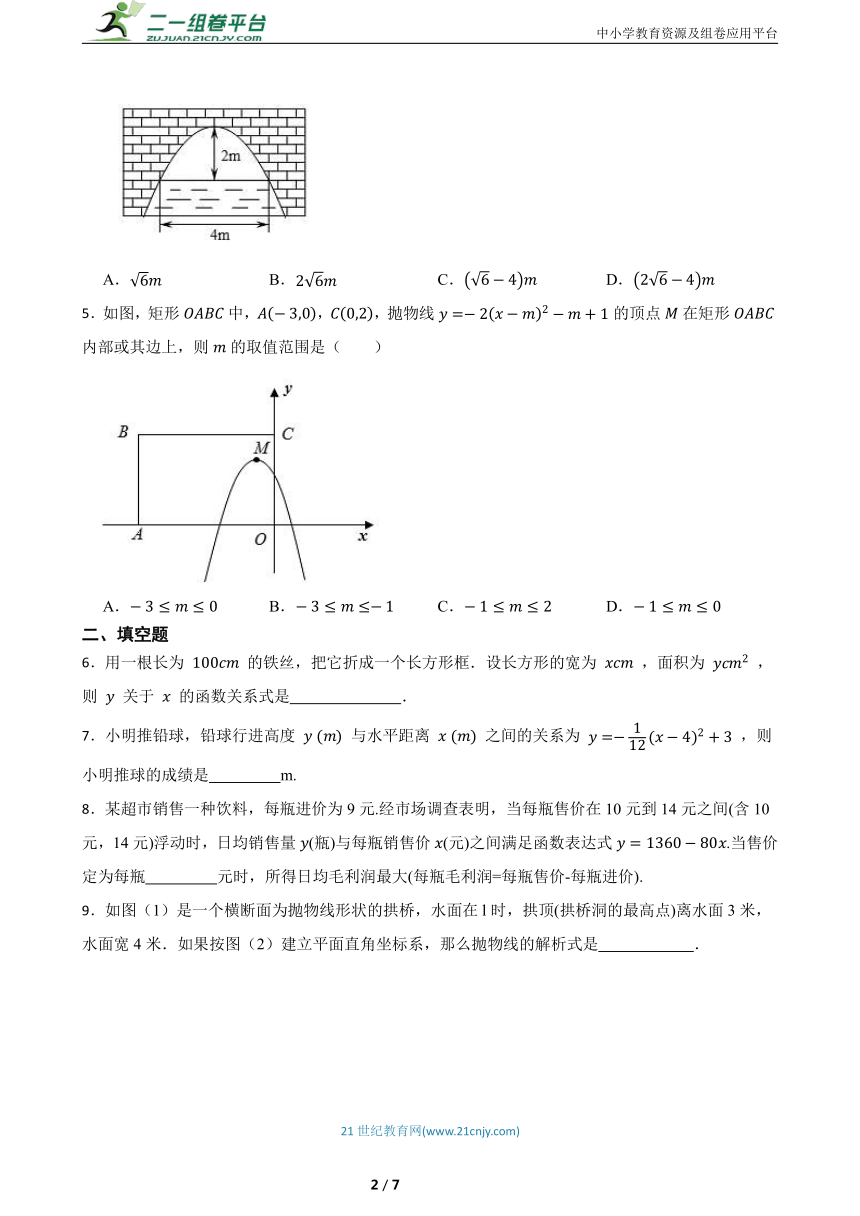
4.如图,一抛物线型拱桥,当拱顶到水面的距离为2m时,水面宽度为4m.那么水位下降1m时,水面的宽度为( )
A. B. C. D.
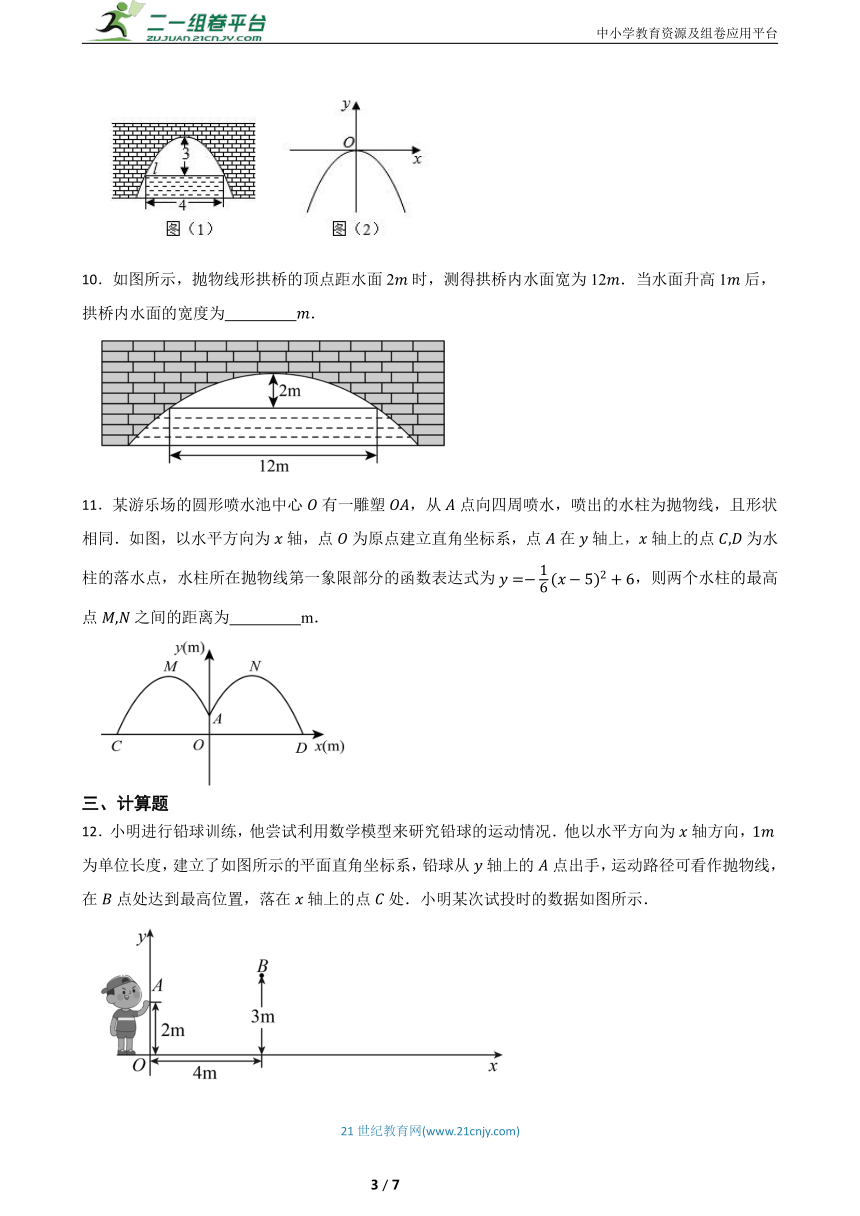
5.如图,矩形中,,,抛物线的顶点在矩形内部或其边上,则的取值范围是( )
A. B. C. D.
二、填空题
6.用一根长为 的铁丝,把它折成一个长方形框.设长方形的宽为 ,面积为 ,则 关于 的函数关系式是 .
7.小明推铅球,铅球行进高度 与水平距离 之间的关系为 ,则小明推球的成绩是 m.
8.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当每瓶售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数表达式.当售价定为每瓶 元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).
9.如图(1)是一个横断面为抛物线形状的拱桥,水面在l时,拱顶(拱桥洞的最高点)离水面3米,水面宽4米.如果按图(2)建立平面直角坐标系,那么抛物线的解析式是 .
10.如图所示,抛物线形拱桥的顶点距水面2时,测得拱桥内水面宽为12.当水面升高1后,拱桥内水面的宽度为 .
11.某游乐场的圆形喷水池中心有一雕塑,从点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为轴,点为原点建立直角坐标系,点在轴上,轴上的点为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为,则两个水柱的最高点之间的距离为 m.
三、计算题
12.小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,铅球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处.小明某次试投时的数据如图所示.
(1)根据图中信息,求出铅球路径所在抛物线的表达式;
(2)若铅球投掷距离(铅球落地点与出手点的水平距离的长度)不小于,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.
13.某商店销售某种特产商品,以每千克12元购进,按每千克16元销售时,每天可售出100千克,经市场调查发现,单价每涨1元,每天的销售量就减少10千克.
(1)若该商店销售这种特产商品想要每天获利480元,并且尽可能让利于顾客,那么每千克特产商品的售价应为多少元?
(2)通过计算说明,每千克特产商品售价为多少元时,每天销售这种特产商品获利最大,最大利润是多少元?
四、解答题
14.商场购进一批儿童智力玩具,调查发现:该玩具的月销售量y(个)与销售单价x(元)之间满足一次函数关系,下表是销售单价与月销售量、月销售利润的对应值分别如下:
月销售单价x(元/个) 30 35 40 45
月销售量y(个) 230 180 130 m
月销售利润w(元) 2300 2700 2600 2000
(1)直接写出y与x的函数关系式 ;
(2)根据以上信息填空:
①m= ;该商场购进玩具单价 元/个;
②求w与x的函数关系式,并求出当销售单价x定为多少时,月销售利润最大?
(3)由于生产玩具成本增加,商场购进玩具单价提高n元/个(0<n≤7,n为整数),商场规定每件玩具售价不能低于40元/个,该商场在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2340元,则n的值是 .
15.“卢沟晓月”是著名的北京八景之一,每当黎明斜月西沉,月色倒影水中,更显明媚饺洁.古时乾隆皇帝曾在秋日路过卢沟桥,赋诗“半钩留照三秋淡,一练分波平镜明”于此,并题“卢沟晓月”,立碑于桥头.卢沟桥主桥拱可以近似看作抛物线,桥拱在水面的跨度约为20米,若按如图所示的方式建立平面直角坐标系,则主桥拱所在抛物线可以表示为,求主桥拱最高点与其在水中倒影之间的距离.
五、综合题
16.为了改善小区环境,某小区决定在一块一边靠墙(墙长)的空地上修建一个矩形小花园,小花园一边靠墙,另三边用总长的栅栏围住,如下图所示.若设矩形小花园边的长为,面积为.
AI
(1)求与之间的函数关系式;
(2)当菜地面积为时,栅栏的三边长各为多少?
17.2023年“五一”假期,昆明校场路蓝花楹主题公园成为热门网红打卡地后,公园开始售卖蓝花楹主题雪糕,每根成本价为3元,经调查,每天的销售量(根)与每根的售价(元)之间的函数关系式如图所示.
(1)求与的函数关系式;
(2)设每天的总利润(元),若每根雪糕的售价为整数,则售价定为多少元时,获利最大?最大利润是多少?
18.某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.
(1)求该商品每月的销售量(件)与销售单价(元)之间的函数关系式:(不需要求自变量取值范围)
(2)若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?
(3)为了每月所获利润最大,该商品销售单价应定为多少元?
答案解析部分
1.【答案】D
【知识点】二次函数的实际应用-拱桥问题
2.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
3.【答案】B
【知识点】二次函数的实际应用-几何问题
4.【答案】B
【知识点】二次函数的实际应用-拱桥问题
5.【答案】D
【知识点】矩形的性质;二次函数的实际应用-几何问题
6.【答案】
【知识点】二次函数的实际应用-几何问题
7.【答案】10
【知识点】二次函数的实际应用-抛球问题
8.【答案】13
【知识点】二次函数的实际应用-销售问题
9.【答案】
【知识点】二次函数的实际应用-拱桥问题
10.【答案】
【知识点】二次函数的实际应用-拱桥问题
11.【答案】10
【知识点】二次函数的实际应用-喷水问题
12.【答案】(1)
(2)能达到优秀
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
13.【答案】(1)18元
(2)销售价格定为19时,才能使平均每天获得的利润最大,最大利润是490元
【知识点】配方法的应用;一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
14.【答案】(1)y=-10x+530
(2)①80;20;②w=-10x2+730x-10600,当销售单价x定为36.5元时,月销售利润最大,最大利润是2722.5元
(3)2
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
15.【答案】米
【知识点】二次函数的实际应用-拱桥问题
16.【答案】(1)
(2),,
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
17.【答案】(1)
(2)每根雪糕的售价定为9元时或者10元时,获利最大,最大利润是420元
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
18.【答案】(1)
(2)销售单价应定为70元
(3)80元
【知识点】二次函数的实际应用-销售问题
21世纪教育网(www.21cnjy.com)
5 / 8
2.41二次函数的应用
一、单选题
1.如图是抛物线型拱桥,当拱顶离水面时,水面宽;如果水面下降,则水面宽度增加( )
A. B. C. D.
2.中条山隧道位于山西省运城市盐湖区,这一隧道的建设开创了全省普通公路特长隧道工程建设的先河,也是全国单洞里程最长的隧道工程.如图1是中条山隧道,其截面近似为抛物线型,如图2为截面示意图,线段表示水平的路面,以O为坐标原点所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.经测量,抛物线的顶点P到的距离为,则抛物线的函数表达式为( )
A. B.
C. D.
3.如图,一边靠学校院墙,其它三边用 40 米长的篱笆围成一个矩形花圃,设矩形 ABCD 的边 AB=x 米,面积为 S 平方米,则下面关系式正确的是( )
A. B.
C. D.
4.如图,一抛物线型拱桥,当拱顶到水面的距离为2m时,水面宽度为4m.那么水位下降1m时,水面的宽度为( )
A. B. C. D.
5.如图,矩形中,,,抛物线的顶点在矩形内部或其边上,则的取值范围是( )
A. B. C. D.
二、填空题
6.用一根长为 的铁丝,把它折成一个长方形框.设长方形的宽为 ,面积为 ,则 关于 的函数关系式是 .
7.小明推铅球,铅球行进高度 与水平距离 之间的关系为 ,则小明推球的成绩是 m.
8.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当每瓶售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数表达式.当售价定为每瓶 元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).
9.如图(1)是一个横断面为抛物线形状的拱桥,水面在l时,拱顶(拱桥洞的最高点)离水面3米,水面宽4米.如果按图(2)建立平面直角坐标系,那么抛物线的解析式是 .
10.如图所示,抛物线形拱桥的顶点距水面2时,测得拱桥内水面宽为12.当水面升高1后,拱桥内水面的宽度为 .
11.某游乐场的圆形喷水池中心有一雕塑,从点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为轴,点为原点建立直角坐标系,点在轴上,轴上的点为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为,则两个水柱的最高点之间的距离为 m.
三、计算题
12.小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,铅球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处.小明某次试投时的数据如图所示.
(1)根据图中信息,求出铅球路径所在抛物线的表达式;
(2)若铅球投掷距离(铅球落地点与出手点的水平距离的长度)不小于,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.
13.某商店销售某种特产商品,以每千克12元购进,按每千克16元销售时,每天可售出100千克,经市场调查发现,单价每涨1元,每天的销售量就减少10千克.
(1)若该商店销售这种特产商品想要每天获利480元,并且尽可能让利于顾客,那么每千克特产商品的售价应为多少元?
(2)通过计算说明,每千克特产商品售价为多少元时,每天销售这种特产商品获利最大,最大利润是多少元?
四、解答题
14.商场购进一批儿童智力玩具,调查发现:该玩具的月销售量y(个)与销售单价x(元)之间满足一次函数关系,下表是销售单价与月销售量、月销售利润的对应值分别如下:
月销售单价x(元/个) 30 35 40 45
月销售量y(个) 230 180 130 m
月销售利润w(元) 2300 2700 2600 2000
(1)直接写出y与x的函数关系式 ;
(2)根据以上信息填空:
①m= ;该商场购进玩具单价 元/个;
②求w与x的函数关系式,并求出当销售单价x定为多少时,月销售利润最大?
(3)由于生产玩具成本增加,商场购进玩具单价提高n元/个(0<n≤7,n为整数),商场规定每件玩具售价不能低于40元/个,该商场在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2340元,则n的值是 .
15.“卢沟晓月”是著名的北京八景之一,每当黎明斜月西沉,月色倒影水中,更显明媚饺洁.古时乾隆皇帝曾在秋日路过卢沟桥,赋诗“半钩留照三秋淡,一练分波平镜明”于此,并题“卢沟晓月”,立碑于桥头.卢沟桥主桥拱可以近似看作抛物线,桥拱在水面的跨度约为20米,若按如图所示的方式建立平面直角坐标系,则主桥拱所在抛物线可以表示为,求主桥拱最高点与其在水中倒影之间的距离.
五、综合题
16.为了改善小区环境,某小区决定在一块一边靠墙(墙长)的空地上修建一个矩形小花园,小花园一边靠墙,另三边用总长的栅栏围住,如下图所示.若设矩形小花园边的长为,面积为.
AI
(1)求与之间的函数关系式;
(2)当菜地面积为时,栅栏的三边长各为多少?
17.2023年“五一”假期,昆明校场路蓝花楹主题公园成为热门网红打卡地后,公园开始售卖蓝花楹主题雪糕,每根成本价为3元,经调查,每天的销售量(根)与每根的售价(元)之间的函数关系式如图所示.
(1)求与的函数关系式;
(2)设每天的总利润(元),若每根雪糕的售价为整数,则售价定为多少元时,获利最大?最大利润是多少?
18.某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.
(1)求该商品每月的销售量(件)与销售单价(元)之间的函数关系式:(不需要求自变量取值范围)
(2)若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?
(3)为了每月所获利润最大,该商品销售单价应定为多少元?
答案解析部分
1.【答案】D
【知识点】二次函数的实际应用-拱桥问题
2.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
3.【答案】B
【知识点】二次函数的实际应用-几何问题
4.【答案】B
【知识点】二次函数的实际应用-拱桥问题
5.【答案】D
【知识点】矩形的性质;二次函数的实际应用-几何问题
6.【答案】
【知识点】二次函数的实际应用-几何问题
7.【答案】10
【知识点】二次函数的实际应用-抛球问题
8.【答案】13
【知识点】二次函数的实际应用-销售问题
9.【答案】
【知识点】二次函数的实际应用-拱桥问题
10.【答案】
【知识点】二次函数的实际应用-拱桥问题
11.【答案】10
【知识点】二次函数的实际应用-喷水问题
12.【答案】(1)
(2)能达到优秀
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
13.【答案】(1)18元
(2)销售价格定为19时,才能使平均每天获得的利润最大,最大利润是490元
【知识点】配方法的应用;一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
14.【答案】(1)y=-10x+530
(2)①80;20;②w=-10x2+730x-10600,当销售单价x定为36.5元时,月销售利润最大,最大利润是2722.5元
(3)2
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
15.【答案】米
【知识点】二次函数的实际应用-拱桥问题
16.【答案】(1)
(2),,
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
17.【答案】(1)
(2)每根雪糕的售价定为9元时或者10元时,获利最大,最大利润是420元
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
18.【答案】(1)
(2)销售单价应定为70元
(3)80元
【知识点】二次函数的实际应用-销售问题
21世纪教育网(www.21cnjy.com)
5 / 8
