第二章 二次函数综合题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章二次函数综合题
一、单选题
1.二次函数的图象与x轴交点的情况是( )
A.没有交点 B.有一个交点 C.有两个交点 D.与m的值有关
2.已知抛物线 ,(1,y1)与(2,y2)是该抛物线上的两点,则y1与y2的大小关系是( ).
A.y1>y2 B.y13.已知点A(1,a)在抛物线y=x2-4x+5上,则点A关于原点对称的点的坐标为( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
4.若将抛物线向上平移个单位后所得的抛物线记为,则抛物线对应的与之间的函数关系式为( )
A. B.
C. D.
5.已知二次函数的图象与x轴的一个交点坐标是,则关于x的一元二次方程的两个实数根是( )
A., B.,
C., D.,
6.已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④ax2+bx+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣ ,y1)、C(﹣ ,y2)为函数图象上的两点,则y1>y2.其中正确的个数是( )
A.2 B.3 C.4 D.5
7.关于二次函数y=﹣x2+3x﹣4,下列说法中正确的是( )
A.函数图象的对称轴是直线x=﹣3
B.函数的有最小值,最小值为﹣4
C.点A(x1,y1)、B(x2,y2)在函数图象上,当时,y1<y2
D.函数值y随x的增大而增大
8.抛物线y=-2(x-3)2-4的顶点坐标( )
A. B. C. D.
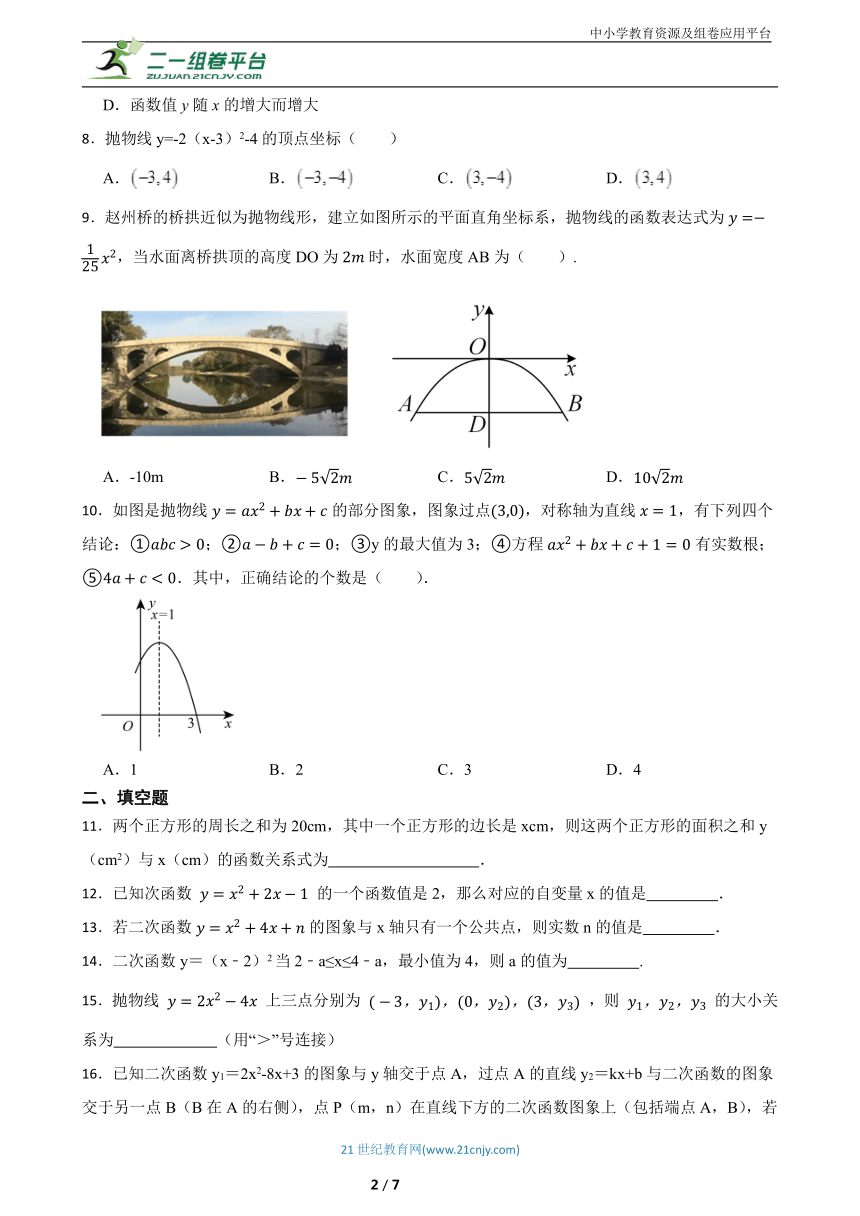
9.赵州桥的桥拱近似为抛物线形,建立如图所示的平面直角坐标系,抛物线的函数表达式为,当水面离桥拱顶的高度DO为时,水面宽度AB为( ).
A.-10m B. C. D.
10.如图是抛物线的部分图象,图象过点,对称轴为直线,有下列四个结论:①;②;③y的最大值为3;④方程有实数根;⑤.其中,正确结论的个数是( ).
A.1 B.2 C.3 D.4
二、填空题
11.两个正方形的周长之和为20cm,其中一个正方形的边长是xcm,则这两个正方形的面积之和y(cm2)与x(cm)的函数关系式为 .
12.已知次函数 的一个函数值是2,那么对应的自变量x的值是 .
13.若二次函数的图象与x轴只有一个公共点,则实数n的值是 .
14.二次函数y=(x﹣2)2当2﹣a≤x≤4﹣a,最小值为4,则a的值为 .
15.抛物线 上三点分别为 ,则 的大小关系为 (用“>”号连接)
16.已知二次函数y1=2x2-8x+3的图象与y轴交于点A,过点A的直线y2=kx+b与二次函数的图象交于另一点B(B在A的右侧),点P(m,n)在直线下方的二次函数图象上(包括端点A,B),若n的最大值与最小值的和为1,则点B的横坐标为 .
三、计算题
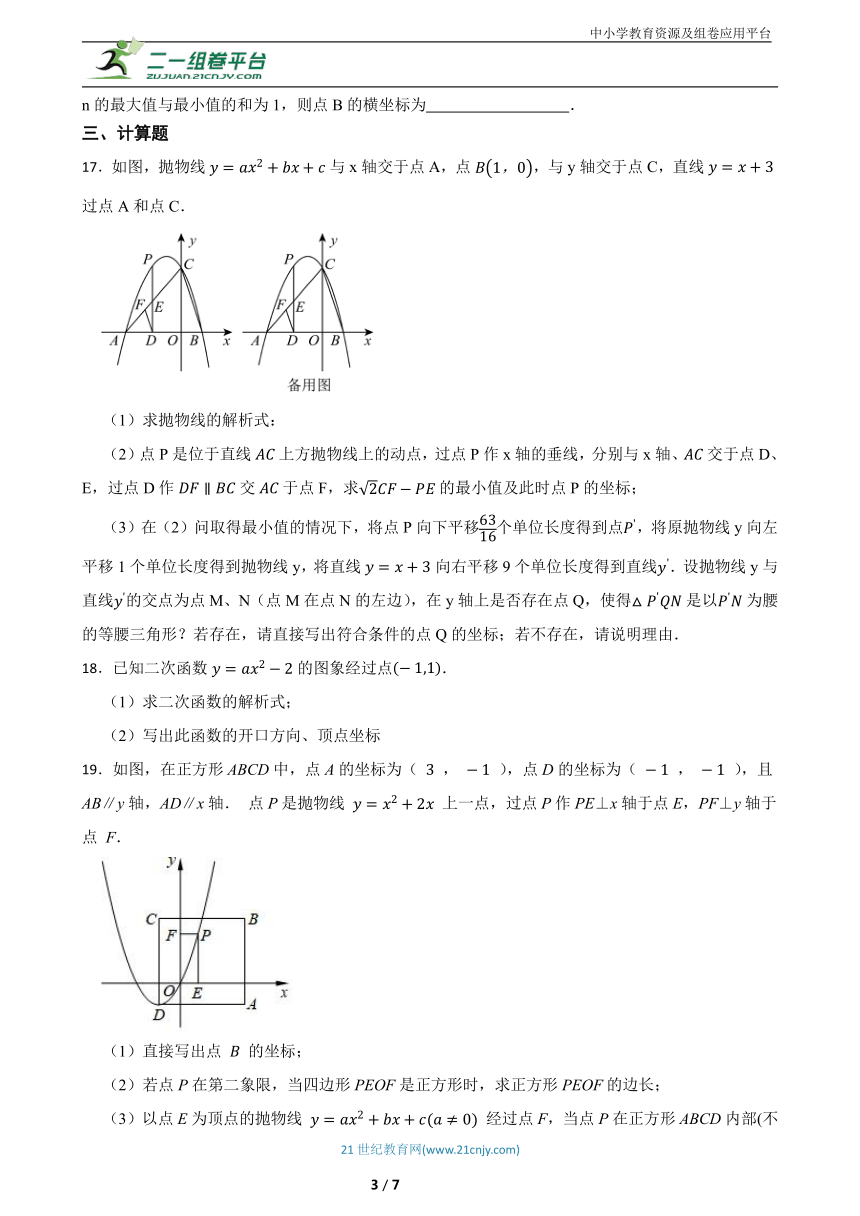
17.如图,抛物线与x轴交于点A,点,与y轴交于点C,直线过点A和点C.
(1)求抛物线的解析式:
(2)点P是位于直线上方抛物线上的动点,过点P作x轴的垂线,分别与x轴、交于点D、E,过点D作交于点F,求的最小值及此时点P的坐标;
(3)在(2)问取得最小值的情况下,将点P向下平移个单位长度得到点,将原抛物线y向左平移1个单位长度得到抛物线y,将直线向右平移9个单位长度得到直线.设抛物线y与直线的交点为点M、N(点M在点N的左边),在y轴上是否存在点Q,使得是以为腰的等腰三角形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.
18.已知二次函数的图象经过点.
(1)求二次函数的解析式;
(2)写出此函数的开口方向、顶点坐标
19.如图,在正方形ABCD中,点A的坐标为( , ),点D的坐标为( , ),且AB∥y轴,AD∥x轴. 点P是抛物线 上一点,过点P作PE⊥x轴于点E,PF⊥y轴于点 F.
(1)直接写出点 的坐标;
(2)若点P在第二象限,当四边形PEOF是正方形时,求正方形PEOF的边长;
(3)以点E为顶点的抛物线 经过点F,当点P在正方形ABCD内部(不包含边)时,求a的取值范围.
四、解答题
20.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.
21.某商场要经营一种新上市的文具,进价为20元/件,试营业阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)商场的营销部结合实际情况,决定该文具的销售单价不低于30元,且每天的销售量不得少于160件,那么该文具如何定价每天的最大销售利润最大,最大利润是多少.
22.已知二次函数y=ax2+bx+3,几组该函数x与y的对应值如表:
x … ﹣1 1 2 …
y … 0 m 3 …
(1)求此二次函数的解析式;
(2)求m的值.
23.如图,抛物线与x轴负半轴交于点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若D是第四象限内抛物线上一点,且,求四边形的面积;
(3)将△ACO绕平面内点P顺时针旋转后,得到(点A,C,O的对应点分别是点),两点刚好在抛物线上,求,P两点的坐标.
答案解析部分
1.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数y=ax²+bx+c的图象
3.【答案】A
【知识点】关于原点对称的点的坐标特征;二次函数图象上点的坐标特征
4.【答案】D
【知识点】二次函数图象的几何变换
5.【答案】A
【知识点】二次函数图象与坐标轴的交点问题;利用二次函数图象判断一元二次方程根的情况
6.【答案】D
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
7.【答案】C
【知识点】二次函数y=a(x-h)²+k的图象
8.【答案】C
【知识点】二次函数y=a(x-h)²+k的性质
9.【答案】D
【知识点】二次函数的实际应用-拱桥问题
10.【答案】C
【知识点】二次函数图象与系数的关系;利用二次函数图象判断一元二次方程根的情况
11.【答案】y= 2x2﹣10x+25
【知识点】列二次函数关系式
12.【答案】-3或1
【知识点】二次函数图象上点的坐标特征
13.【答案】4
【知识点】二次函数图象与坐标轴的交点问题
14.【答案】4或﹣2
【知识点】二次函数y=a(x-h)²+k的性质
15.【答案】
【知识点】二次函数y=ax²+bx+c的性质
16.【答案】 或
【知识点】二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
17.【答案】(1)
(2),
(3)或或或
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式;两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】(1)
(2)二次函数的开口向上,顶点坐标为
【知识点】待定系数法求二次函数解析式
19.【答案】(1) ( , );
(2)设点 ( , ).
当四边形 是正方形时, ,
当点 在第二象限时,有 .
解得 , .
∵ ,
∴ .
∴正方形 的边长为 .
(3)设点 ( , ),则点E( , ),则点F( , ).
∵ 为抛物线顶点,
∴该抛物线解析式为 .
∵抛物线经过点 ,
∴ ,化简得 .
对于 ,令 ,解得 ; 令 ,解得 .
∵点 在正方形 内部,
∴ < < ,且 .
①当 < < 时
由反比例函数性质知 ,∴ < .
②当 < < 时
由反比例函数性质知 ,∴ > .
【知识点】反比例函数的图象;反比例函数的性质;正方形的性质;二次函数图象上点的坐标特征
20.【答案】解:作AE⊥BC,
在Rt△ABE中,∠B=30°,
则AE= AB= x,
∵四边形ABCD是等腰梯形,
∴AD+BC=60﹣AB﹣CD=60﹣2x,
∴S= (AD+BC)×AE= (60﹣2x)× x=﹣ x2+15x(0<x<60).
【知识点】列二次函数关系式
21.【答案】(1);(2)34;2240;
【知识点】二次函数的实际应用-销售问题
22.【答案】(1)解:由题得,将x=﹣1,y=0和 x=2,y=3代入得,
,
解得,
y=﹣x2+2x+3;
(2)解:将 x=1,y=m 代入得,
m=﹣12+2×1+3=4.
【知识点】函数值;待定系数法求二次函数解析式
23.【答案】(1)
(2)
(3),
【知识点】待定系数法求二次函数解析式;旋转的性质;二次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 7
第二章二次函数综合题
一、单选题
1.二次函数的图象与x轴交点的情况是( )
A.没有交点 B.有一个交点 C.有两个交点 D.与m的值有关
2.已知抛物线 ,(1,y1)与(2,y2)是该抛物线上的两点,则y1与y2的大小关系是( ).
A.y1>y2 B.y1
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
4.若将抛物线向上平移个单位后所得的抛物线记为,则抛物线对应的与之间的函数关系式为( )
A. B.
C. D.
5.已知二次函数的图象与x轴的一个交点坐标是,则关于x的一元二次方程的两个实数根是( )
A., B.,
C., D.,
6.已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④ax2+bx+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣ ,y1)、C(﹣ ,y2)为函数图象上的两点,则y1>y2.其中正确的个数是( )
A.2 B.3 C.4 D.5
7.关于二次函数y=﹣x2+3x﹣4,下列说法中正确的是( )
A.函数图象的对称轴是直线x=﹣3
B.函数的有最小值,最小值为﹣4
C.点A(x1,y1)、B(x2,y2)在函数图象上,当时,y1<y2
D.函数值y随x的增大而增大
8.抛物线y=-2(x-3)2-4的顶点坐标( )
A. B. C. D.
9.赵州桥的桥拱近似为抛物线形,建立如图所示的平面直角坐标系,抛物线的函数表达式为,当水面离桥拱顶的高度DO为时,水面宽度AB为( ).
A.-10m B. C. D.
10.如图是抛物线的部分图象,图象过点,对称轴为直线,有下列四个结论:①;②;③y的最大值为3;④方程有实数根;⑤.其中,正确结论的个数是( ).
A.1 B.2 C.3 D.4
二、填空题
11.两个正方形的周长之和为20cm,其中一个正方形的边长是xcm,则这两个正方形的面积之和y(cm2)与x(cm)的函数关系式为 .
12.已知次函数 的一个函数值是2,那么对应的自变量x的值是 .
13.若二次函数的图象与x轴只有一个公共点,则实数n的值是 .
14.二次函数y=(x﹣2)2当2﹣a≤x≤4﹣a,最小值为4,则a的值为 .
15.抛物线 上三点分别为 ,则 的大小关系为 (用“>”号连接)
16.已知二次函数y1=2x2-8x+3的图象与y轴交于点A,过点A的直线y2=kx+b与二次函数的图象交于另一点B(B在A的右侧),点P(m,n)在直线下方的二次函数图象上(包括端点A,B),若n的最大值与最小值的和为1,则点B的横坐标为 .
三、计算题
17.如图,抛物线与x轴交于点A,点,与y轴交于点C,直线过点A和点C.
(1)求抛物线的解析式:
(2)点P是位于直线上方抛物线上的动点,过点P作x轴的垂线,分别与x轴、交于点D、E,过点D作交于点F,求的最小值及此时点P的坐标;
(3)在(2)问取得最小值的情况下,将点P向下平移个单位长度得到点,将原抛物线y向左平移1个单位长度得到抛物线y,将直线向右平移9个单位长度得到直线.设抛物线y与直线的交点为点M、N(点M在点N的左边),在y轴上是否存在点Q,使得是以为腰的等腰三角形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.
18.已知二次函数的图象经过点.
(1)求二次函数的解析式;
(2)写出此函数的开口方向、顶点坐标
19.如图,在正方形ABCD中,点A的坐标为( , ),点D的坐标为( , ),且AB∥y轴,AD∥x轴. 点P是抛物线 上一点,过点P作PE⊥x轴于点E,PF⊥y轴于点 F.
(1)直接写出点 的坐标;
(2)若点P在第二象限,当四边形PEOF是正方形时,求正方形PEOF的边长;
(3)以点E为顶点的抛物线 经过点F,当点P在正方形ABCD内部(不包含边)时,求a的取值范围.
四、解答题
20.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.
21.某商场要经营一种新上市的文具,进价为20元/件,试营业阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)商场的营销部结合实际情况,决定该文具的销售单价不低于30元,且每天的销售量不得少于160件,那么该文具如何定价每天的最大销售利润最大,最大利润是多少.
22.已知二次函数y=ax2+bx+3,几组该函数x与y的对应值如表:
x … ﹣1 1 2 …
y … 0 m 3 …
(1)求此二次函数的解析式;
(2)求m的值.
23.如图,抛物线与x轴负半轴交于点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若D是第四象限内抛物线上一点,且,求四边形的面积;
(3)将△ACO绕平面内点P顺时针旋转后,得到(点A,C,O的对应点分别是点),两点刚好在抛物线上,求,P两点的坐标.
答案解析部分
1.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数y=ax²+bx+c的图象
3.【答案】A
【知识点】关于原点对称的点的坐标特征;二次函数图象上点的坐标特征
4.【答案】D
【知识点】二次函数图象的几何变换
5.【答案】A
【知识点】二次函数图象与坐标轴的交点问题;利用二次函数图象判断一元二次方程根的情况
6.【答案】D
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
7.【答案】C
【知识点】二次函数y=a(x-h)²+k的图象
8.【答案】C
【知识点】二次函数y=a(x-h)²+k的性质
9.【答案】D
【知识点】二次函数的实际应用-拱桥问题
10.【答案】C
【知识点】二次函数图象与系数的关系;利用二次函数图象判断一元二次方程根的情况
11.【答案】y= 2x2﹣10x+25
【知识点】列二次函数关系式
12.【答案】-3或1
【知识点】二次函数图象上点的坐标特征
13.【答案】4
【知识点】二次函数图象与坐标轴的交点问题
14.【答案】4或﹣2
【知识点】二次函数y=a(x-h)²+k的性质
15.【答案】
【知识点】二次函数y=ax²+bx+c的性质
16.【答案】 或
【知识点】二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
17.【答案】(1)
(2),
(3)或或或
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式;两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】(1)
(2)二次函数的开口向上,顶点坐标为
【知识点】待定系数法求二次函数解析式
19.【答案】(1) ( , );
(2)设点 ( , ).
当四边形 是正方形时, ,
当点 在第二象限时,有 .
解得 , .
∵ ,
∴ .
∴正方形 的边长为 .
(3)设点 ( , ),则点E( , ),则点F( , ).
∵ 为抛物线顶点,
∴该抛物线解析式为 .
∵抛物线经过点 ,
∴ ,化简得 .
对于 ,令 ,解得 ; 令 ,解得 .
∵点 在正方形 内部,
∴ < < ,且 .
①当 < < 时
由反比例函数性质知 ,∴ < .
②当 < < 时
由反比例函数性质知 ,∴ > .
【知识点】反比例函数的图象;反比例函数的性质;正方形的性质;二次函数图象上点的坐标特征
20.【答案】解:作AE⊥BC,
在Rt△ABE中,∠B=30°,
则AE= AB= x,
∵四边形ABCD是等腰梯形,
∴AD+BC=60﹣AB﹣CD=60﹣2x,
∴S= (AD+BC)×AE= (60﹣2x)× x=﹣ x2+15x(0<x<60).
【知识点】列二次函数关系式
21.【答案】(1);(2)34;2240;
【知识点】二次函数的实际应用-销售问题
22.【答案】(1)解:由题得,将x=﹣1,y=0和 x=2,y=3代入得,
,
解得,
y=﹣x2+2x+3;
(2)解:将 x=1,y=m 代入得,
m=﹣12+2×1+3=4.
【知识点】函数值;待定系数法求二次函数解析式
23.【答案】(1)
(2)
(3),
【知识点】待定系数法求二次函数解析式;旋转的性质;二次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 7
