2025高考物理专题--复习追及相遇问题 课件(共21张ppt)
文档属性
| 名称 | 2025高考物理专题--复习追及相遇问题 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 329.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
追及、相遇问题
【学习目标】
1.掌握匀变速直线运动的三大基本公式
2.掌握追及、相遇问题的特点。
3.掌握追及、相遇问题的处理方法,能熟练解决追及、相遇问题。
4、通过解决实际问题,培养学生运用物理规律对实际生活中的物理问题进行合理分析的能力。
一、图像类模型
利用运动图像考查追及和相遇问题以选择题为主,解决此类问题一般思路。
1、明确图像
2、对图像中出现的截距、斜率、面积和交点等理解它们的物理意义
3、应用规律找出个各物理量的关系
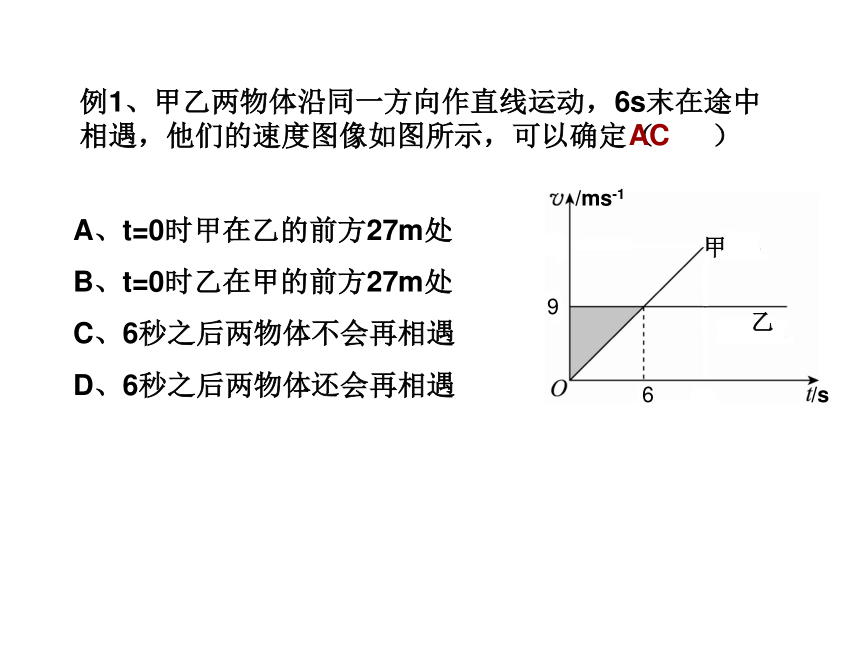
例1、甲乙两物体沿同一方向作直线运动,6s末在途中相遇,他们的速度图像如图所示,可以确定( )
A、t=0时甲在乙的前方27m处
B、t=0时乙在甲的前方27m处
C、6秒之后两物体不会再相遇
D、6秒之后两物体还会再相遇
甲
乙
6
9
AC
/ms-1
/s
二、实际问题模型
基本思路出:确定初始时刻是否在同一位置、同时开始运动。并画物体运动的情景图,抓住一个条件,两个关系。
研究的是两物体在同一时刻到达相同的空间位置的问题。
两个关系:即时间关系和位移关系。通过情景图找出两物体的位移关系。
一个条件:二者速度相等时,往往是能否追上或两者距离最大、最小的临界条件,也是分析判断的切入点。
例2、一汽车从静止开始以1m/s2的加速度前进,车后相距x0为25m处,某人同时开始以6m/s的速度匀速追车,能否追上?如追上,求追上需要的时间;如追不上,求人、车间的最小距离。
(1)当人车速度相等时,两者间距离最小。
v车=v人=at=6m/s t=6s
在这段时间里,人、车的位移分别为:
x人=v人t=6×6=36m
x车=at2/2=1×62/2=18m
由位移关系知:x人< x车+X0,故追不上。
(2)此时,人车间有最小距离:
Δx=x0+x车-x人=25+18-36=7m
(解法一)物理分析法:
人
v/ms-1
汽车
t/s
o
6
T0=6s
α
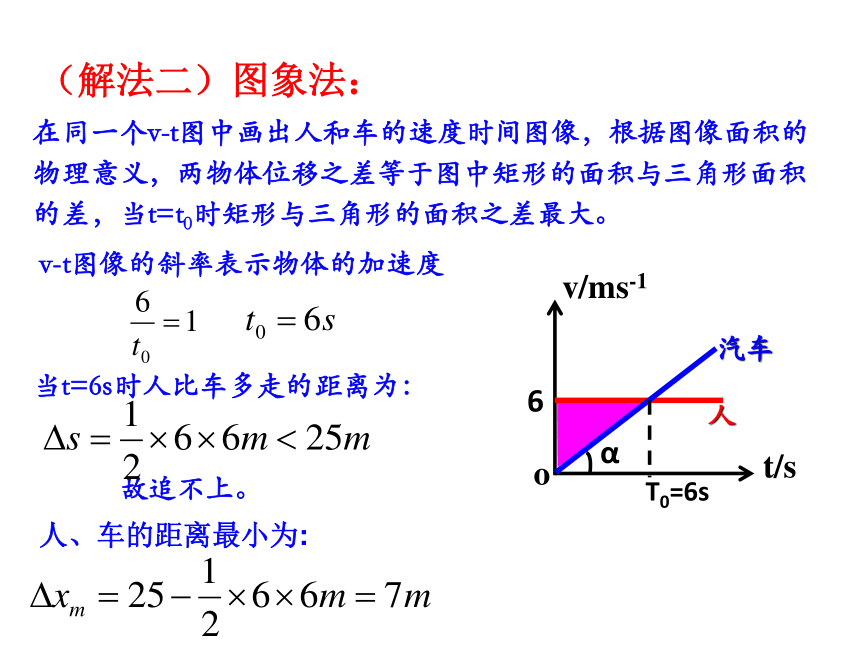
在同一个v-t图中画出人和车的速度时间图像,根据图像面积的物理意义,两物体位移之差等于图中矩形的面积与三角形面积的差,当t=t0时矩形与三角形的面积之差最大。
(解法二)图象法:
v-t图像的斜率表示物体的加速度
当t=6s时人比车多走的距离为:
故追不上。
人、车的距离最小为:
例3、甲乙两物体在同一条直线上同时同地沿同一方向运动,甲初速度6m/s,由于摩擦匀减速直线运动,加速度大小2m/s2,乙做初速度为零,加速度为1m/s2的匀加速直线运动,求
1)甲物体能运动多远?
2)乙此后经多长时间追上甲?
3)乙追上甲之前两物体最大距离是多少?
1) 9m
2) 4.2s
3) 6m
相遇和追及问题的常用解题方法
(2)物理分析法——根据运动学公式,把时间关系渗透到位移关系和速度关系中列式求解。
(1)图象法——正确画出物体运动的v--t图象,根据图象的斜率、截距、面积的物理意义结合速度的特点、时间和位移关系列方程求解。
总结
解决追及、相遇问题要做到:
1、画出两个物体运动的情景示意图或者v-t图象,分析两个物体的运动性质。
2、抓住两个关系,一个条件:
(1)两个关系:时间关系和位移关系
(2)一个条件:即两者速度相等。它往往
是物体间能否追上或(两者)距离最大、
最小的临界条件,也是分析判断的切入点。
总结
C
练习4、甲车在前以15 m/s的速度匀速行驶,乙车在后以9 m/s的速度匀速行驶。当两车相距32m时,甲车开始刹车,加速度大小为1m/s2。问经多长时间乙车可追上甲车?
解:甲车停止后乙再追上甲。
甲车刹车的位移
x甲=v02/2a=152/2=112.5m
乙车的总位移
x乙=x甲+32=144.5m
t=x乙/v乙=144.5/9=16.06s
练习5、一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以一定的加速度做匀加速运动,但警车行驶的最大速度是25m/s.警车发动后刚好用12s的时间追上货车,问:
(1)警车启动时的加速度多大?
(2)警车在追赶货车的过程中,两车间的最大距离是多少?
解:(1)设5.5s内货车位移为s0, 则s0=v0t0=55m
若12s内警车一直做匀加速直线运动,则:at2/2=v0t+s0
解得:a=2.43m/s2
此时警车的速度为:v=at=29.2m/s>25m/s
因此警车的运动应为:先做匀加速直线运动,达到最大速度25m/s后做匀速直线运动
设其加速时间为t1,则: vm=at1
at12/2 +vm(t-t1)=v0t+s0
由以上各式可解得:a=2.5 m/s2
(2)当警车的速度与货车的速度相等时,两者间的距离最大,设所需时间为t2,则:v0=at2 即 t2=4 s
两车间的最大距离为:sm=v0t2+s0-at22/2=75m
追及、相遇问题
【学习目标】
1.掌握匀变速直线运动的三大基本公式
2.掌握追及、相遇问题的特点。
3.掌握追及、相遇问题的处理方法,能熟练解决追及、相遇问题。
4、通过解决实际问题,培养学生运用物理规律对实际生活中的物理问题进行合理分析的能力。
一、图像类模型
利用运动图像考查追及和相遇问题以选择题为主,解决此类问题一般思路。
1、明确图像
2、对图像中出现的截距、斜率、面积和交点等理解它们的物理意义
3、应用规律找出个各物理量的关系
例1、甲乙两物体沿同一方向作直线运动,6s末在途中相遇,他们的速度图像如图所示,可以确定( )
A、t=0时甲在乙的前方27m处
B、t=0时乙在甲的前方27m处
C、6秒之后两物体不会再相遇
D、6秒之后两物体还会再相遇
甲
乙
6
9
AC
/ms-1
/s
二、实际问题模型
基本思路出:确定初始时刻是否在同一位置、同时开始运动。并画物体运动的情景图,抓住一个条件,两个关系。
研究的是两物体在同一时刻到达相同的空间位置的问题。
两个关系:即时间关系和位移关系。通过情景图找出两物体的位移关系。
一个条件:二者速度相等时,往往是能否追上或两者距离最大、最小的临界条件,也是分析判断的切入点。
例2、一汽车从静止开始以1m/s2的加速度前进,车后相距x0为25m处,某人同时开始以6m/s的速度匀速追车,能否追上?如追上,求追上需要的时间;如追不上,求人、车间的最小距离。
(1)当人车速度相等时,两者间距离最小。
v车=v人=at=6m/s t=6s
在这段时间里,人、车的位移分别为:
x人=v人t=6×6=36m
x车=at2/2=1×62/2=18m
由位移关系知:x人< x车+X0,故追不上。
(2)此时,人车间有最小距离:
Δx=x0+x车-x人=25+18-36=7m
(解法一)物理分析法:
人
v/ms-1
汽车
t/s
o
6
T0=6s
α
在同一个v-t图中画出人和车的速度时间图像,根据图像面积的物理意义,两物体位移之差等于图中矩形的面积与三角形面积的差,当t=t0时矩形与三角形的面积之差最大。
(解法二)图象法:
v-t图像的斜率表示物体的加速度
当t=6s时人比车多走的距离为:
故追不上。
人、车的距离最小为:
例3、甲乙两物体在同一条直线上同时同地沿同一方向运动,甲初速度6m/s,由于摩擦匀减速直线运动,加速度大小2m/s2,乙做初速度为零,加速度为1m/s2的匀加速直线运动,求
1)甲物体能运动多远?
2)乙此后经多长时间追上甲?
3)乙追上甲之前两物体最大距离是多少?
1) 9m
2) 4.2s
3) 6m
相遇和追及问题的常用解题方法
(2)物理分析法——根据运动学公式,把时间关系渗透到位移关系和速度关系中列式求解。
(1)图象法——正确画出物体运动的v--t图象,根据图象的斜率、截距、面积的物理意义结合速度的特点、时间和位移关系列方程求解。
总结
解决追及、相遇问题要做到:
1、画出两个物体运动的情景示意图或者v-t图象,分析两个物体的运动性质。
2、抓住两个关系,一个条件:
(1)两个关系:时间关系和位移关系
(2)一个条件:即两者速度相等。它往往
是物体间能否追上或(两者)距离最大、
最小的临界条件,也是分析判断的切入点。
总结
C
练习4、甲车在前以15 m/s的速度匀速行驶,乙车在后以9 m/s的速度匀速行驶。当两车相距32m时,甲车开始刹车,加速度大小为1m/s2。问经多长时间乙车可追上甲车?
解:甲车停止后乙再追上甲。
甲车刹车的位移
x甲=v02/2a=152/2=112.5m
乙车的总位移
x乙=x甲+32=144.5m
t=x乙/v乙=144.5/9=16.06s
练习5、一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以一定的加速度做匀加速运动,但警车行驶的最大速度是25m/s.警车发动后刚好用12s的时间追上货车,问:
(1)警车启动时的加速度多大?
(2)警车在追赶货车的过程中,两车间的最大距离是多少?
解:(1)设5.5s内货车位移为s0, 则s0=v0t0=55m
若12s内警车一直做匀加速直线运动,则:at2/2=v0t+s0
解得:a=2.43m/s2
此时警车的速度为:v=at=29.2m/s>25m/s
因此警车的运动应为:先做匀加速直线运动,达到最大速度25m/s后做匀速直线运动
设其加速时间为t1,则: vm=at1
at12/2 +vm(t-t1)=v0t+s0
由以上各式可解得:a=2.5 m/s2
(2)当警车的速度与货车的速度相等时,两者间的距离最大,设所需时间为t2,则:v0=at2 即 t2=4 s
两车间的最大距离为:sm=v0t2+s0-at22/2=75m
同课章节目录
