2024-2025学年浙江省杭州市保俶塔实验教育集团九年级(上)期中数学试卷(无答案)
文档属性
| 名称 | 2024-2025学年浙江省杭州市保俶塔实验教育集团九年级(上)期中数学试卷(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 16:29:12 | ||
图片预览

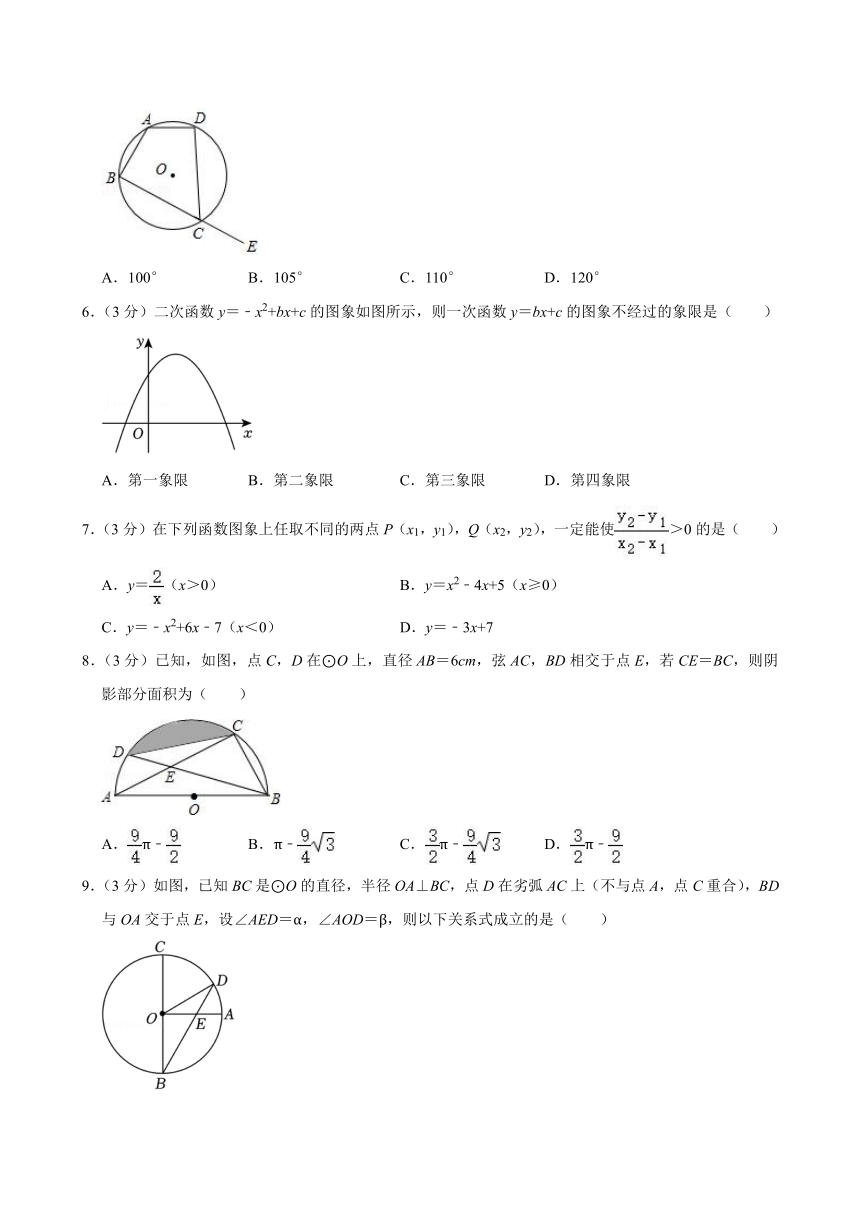

文档简介
2024-2025学年浙江省杭州市保俶塔实验教育集团九年级(上)期中数学试卷
一.选择题(每小题3分,共30分,每小题只有一个选项符合题意)
1.(3分)下列各式中,y是x的二次函数的是( )
A. B.y=2x﹣3 C.y=x2﹣3 D.
2.(3分)盒子里有10个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球
B.摸出红球的可能性最大
C.不可能是黑球
D.摸出黄球的可能性最小
3.(3分)已知⊙O与点P在同一平面内,如果⊙O的半径为5,线段OP的长为3,则下列说法正确的是( )
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法判断点P与⊙O的位置关系
4.(3分)如图,将△ABC绕点A顺时针旋转90°得到△ADE,若∠DAE=50°,则∠CAD=( )
A.30° B.40° C.50° D.90°
5.(3分)如图,四边形ABCD是⊙O的内接四边形,E在BC的延长线上,若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )
A.100° B.105° C.110° D.120°
6.(3分)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(3分)在下列函数图象上任取不同的两点P(x1,y1),Q(x2,y2),一定能使>0的是( )
A.y=(x>0) B.y=x2﹣4x+5(x≥0)
C.y=﹣x2+6x﹣7(x<0) D.y=﹣3x+7
8.(3分)已知,如图,点C,D在⊙O上,直径AB=6cm,弦AC,BD相交于点E,若CE=BC,则阴影部分面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
9.(3分)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则以下关系式成立的是( )
A.2α+β=180° B.2α﹣β=90° C.3α+β=180° D.3α﹣β=90°
10.(3分)已知二次函数y=4(x﹣a)(x﹣b)+1(a,b是实数),设该函数最小值为k,下列说法正确的是( )
A.若2<a<3,2<b<3,则k<0
B.若2<a<3,2<b<3,则0<k<1
C.若2<a<3,3<b<4,则k<﹣3
D.若2<a<3,3<b<4,则k>﹣3
二.填空题(每题3分,共18分)
11.(3分)从,0,3这三个数中随机选择一个数,则这个数为无理数的概率是 .
12.(3分)已知二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
x ﹣3 ﹣2 ﹣1 0 1 …
y … 0 3 4 3 m …
根据表格内容,则m的值为 .
13.(3分)如图所示,AD为⊙O的直径,点B、C在圆上,∠B=60°,则∠CAD= .
14.(3分)一个袋子中装有3个红球和2个黄球,它们除颜色外,其他都相同.现将n个绿球(与红、黄球除颜色外,其他都相同)放入袋中摇均匀,从袋中随机摸出一个球,记下颜色,再把它放回袋中,不断重复上述的过程,共摸了500次,其中60次摸到红球.则估计n的值为 .
15.(3分)已知二次函数y=ax2+4ax+a+1(a为常数,且a<0)的图象经过P(x1,y1)、Q(3,y2),当y1>y2时,则x1的取值范围为 .
16.(3分)如图,在Rt△ABC中,∠ACB=90°,以其三边为边在AB的同侧作三个正方形,点I在DE上,以EF为直径的圆交直线AB于点M,N.若I为DE的中点,AB=5,则MN= .
三.解答题(本大题共8题,共72分)
17.(8分)已知二次函数y=ax2+bx+3的图象经过点(﹣3,0),(2,﹣5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(﹣2,3)是否在这个二次函数的图象上?
18.(8分)在一个不透明的盒子中,装有3个分别写有数字3,﹣5,7的小球,它们的形状、大小、质地完全相同,搅拌均匀后,先从盒子里随机抽取1个小球,记下小球上的数字后放回盒子,搅拌均匀后再随机取出1个小球,再记下小球上的数字.
(1)用列表法或树状图法中的一种方法,写出所有可能出现的结果;
(2)求两次取出的小球上数字的和是正数的概率.
19.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)△ABC的外接圆的半径为 ;
(2)将△ABC绕点B顺时针旋转90°后得到△A1BC1,请在图中画出△A1BC1;
(3)在(2)的条件下,求出点C经过的路径长.
20.(8分)如图,AC为⊙O的直径,BD是弦,且AC⊥BD于点E.连接AB、OB、BC.
(1)求证:∠CBO=∠ABD;
(2)若AE=2,CE=8,求弦BD的长.
21.(8分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为x m(如图),养殖场的总面积为ym2.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)当x为多少时,矩形养殖场的总面积最大?最大值为多少?
22.(10分)如图1,CD是△ABC的外角∠ECB的角平分线,与△ABC的外接圆⊙O交于点D.
(1)若∠ECB=120°,
①求所对圆心角的度数;
②连结DB,DA,求证:△ABD是等边三角形.
(2)如图2,若∠ADB=45°,AB=2,求△ABD的面积.
23.(10分)设二次函数y=x2+bx+c(b,c是常数)的图象与x轴交于A,B两点.
(1)若A,B两点的坐标分别为(1,0),(3,0),求函数y的表达式及其图象的对称轴.
(2)在(1)的条件下,若函数y的图象上有P(x1,y1),Q(x2,y2)两点,且.求证:y1﹣y2>0.
(3)若函数y的表达式可以写成y=(x﹣m)(x﹣m﹣1)的形式,若0<m<2,求b+c的取值范围.
24.(12分)如图1,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F,作AH⊥DG于点H.
(1)求证:∠FGC=∠AGD;
(2)若∠GDC=30°,GC平分∠DGF,请在图2中补全图形并求出的值;
(3)猜想线段DH,HG,CG之间的数量关系,并证明你的结论.
一.选择题(每小题3分,共30分,每小题只有一个选项符合题意)
1.(3分)下列各式中,y是x的二次函数的是( )
A. B.y=2x﹣3 C.y=x2﹣3 D.
2.(3分)盒子里有10个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球
B.摸出红球的可能性最大
C.不可能是黑球
D.摸出黄球的可能性最小
3.(3分)已知⊙O与点P在同一平面内,如果⊙O的半径为5,线段OP的长为3,则下列说法正确的是( )
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法判断点P与⊙O的位置关系
4.(3分)如图,将△ABC绕点A顺时针旋转90°得到△ADE,若∠DAE=50°,则∠CAD=( )
A.30° B.40° C.50° D.90°
5.(3分)如图,四边形ABCD是⊙O的内接四边形,E在BC的延长线上,若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )
A.100° B.105° C.110° D.120°
6.(3分)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(3分)在下列函数图象上任取不同的两点P(x1,y1),Q(x2,y2),一定能使>0的是( )
A.y=(x>0) B.y=x2﹣4x+5(x≥0)
C.y=﹣x2+6x﹣7(x<0) D.y=﹣3x+7
8.(3分)已知,如图,点C,D在⊙O上,直径AB=6cm,弦AC,BD相交于点E,若CE=BC,则阴影部分面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
9.(3分)如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则以下关系式成立的是( )
A.2α+β=180° B.2α﹣β=90° C.3α+β=180° D.3α﹣β=90°
10.(3分)已知二次函数y=4(x﹣a)(x﹣b)+1(a,b是实数),设该函数最小值为k,下列说法正确的是( )
A.若2<a<3,2<b<3,则k<0
B.若2<a<3,2<b<3,则0<k<1
C.若2<a<3,3<b<4,则k<﹣3
D.若2<a<3,3<b<4,则k>﹣3
二.填空题(每题3分,共18分)
11.(3分)从,0,3这三个数中随机选择一个数,则这个数为无理数的概率是 .
12.(3分)已知二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
x ﹣3 ﹣2 ﹣1 0 1 …
y … 0 3 4 3 m …
根据表格内容,则m的值为 .
13.(3分)如图所示,AD为⊙O的直径,点B、C在圆上,∠B=60°,则∠CAD= .
14.(3分)一个袋子中装有3个红球和2个黄球,它们除颜色外,其他都相同.现将n个绿球(与红、黄球除颜色外,其他都相同)放入袋中摇均匀,从袋中随机摸出一个球,记下颜色,再把它放回袋中,不断重复上述的过程,共摸了500次,其中60次摸到红球.则估计n的值为 .
15.(3分)已知二次函数y=ax2+4ax+a+1(a为常数,且a<0)的图象经过P(x1,y1)、Q(3,y2),当y1>y2时,则x1的取值范围为 .
16.(3分)如图,在Rt△ABC中,∠ACB=90°,以其三边为边在AB的同侧作三个正方形,点I在DE上,以EF为直径的圆交直线AB于点M,N.若I为DE的中点,AB=5,则MN= .
三.解答题(本大题共8题,共72分)
17.(8分)已知二次函数y=ax2+bx+3的图象经过点(﹣3,0),(2,﹣5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(﹣2,3)是否在这个二次函数的图象上?
18.(8分)在一个不透明的盒子中,装有3个分别写有数字3,﹣5,7的小球,它们的形状、大小、质地完全相同,搅拌均匀后,先从盒子里随机抽取1个小球,记下小球上的数字后放回盒子,搅拌均匀后再随机取出1个小球,再记下小球上的数字.
(1)用列表法或树状图法中的一种方法,写出所有可能出现的结果;
(2)求两次取出的小球上数字的和是正数的概率.
19.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)△ABC的外接圆的半径为 ;
(2)将△ABC绕点B顺时针旋转90°后得到△A1BC1,请在图中画出△A1BC1;
(3)在(2)的条件下,求出点C经过的路径长.
20.(8分)如图,AC为⊙O的直径,BD是弦,且AC⊥BD于点E.连接AB、OB、BC.
(1)求证:∠CBO=∠ABD;
(2)若AE=2,CE=8,求弦BD的长.
21.(8分)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为x m(如图),养殖场的总面积为ym2.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)当x为多少时,矩形养殖场的总面积最大?最大值为多少?
22.(10分)如图1,CD是△ABC的外角∠ECB的角平分线,与△ABC的外接圆⊙O交于点D.
(1)若∠ECB=120°,
①求所对圆心角的度数;
②连结DB,DA,求证:△ABD是等边三角形.
(2)如图2,若∠ADB=45°,AB=2,求△ABD的面积.
23.(10分)设二次函数y=x2+bx+c(b,c是常数)的图象与x轴交于A,B两点.
(1)若A,B两点的坐标分别为(1,0),(3,0),求函数y的表达式及其图象的对称轴.
(2)在(1)的条件下,若函数y的图象上有P(x1,y1),Q(x2,y2)两点,且.求证:y1﹣y2>0.
(3)若函数y的表达式可以写成y=(x﹣m)(x﹣m﹣1)的形式,若0<m<2,求b+c的取值范围.
24.(12分)如图1,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F,作AH⊥DG于点H.
(1)求证:∠FGC=∠AGD;
(2)若∠GDC=30°,GC平分∠DGF,请在图2中补全图形并求出的值;
(3)猜想线段DH,HG,CG之间的数量关系,并证明你的结论.
同课章节目录
