【小升初复习】小学数学公式定律大全
图片预览



文档简介
小学数学公式定律大全
目 录
一、图形与几何 ..............................................................................................................1
长方形 ........................................................................................................................................ 1
正方形 ........................................................................................................................................ 1
平行四边形 ................................................................................................................................ 1
三角形 ........................................................................................................................................ 2
梯形 ............................................................................................................................................ 2
圆 ................................................................................................................................................ 3
长方体 ........................................................................................................................................ 4
正方体 ........................................................................................................................................ 4
圆柱 ............................................................................................................................................ 4
圆锥 ............................................................................................................................................ 5
二、数的认识 ..................................................................................................................6
三、算术概念 ..................................................................................................................8
★ 加法交换律 .............................................................................................................................. 8
★ 加法结合律 .............................................................................................................................. 8
★ 乘法交换律 .............................................................................................................................. 8
★ 乘法结合律 .............................................................................................................................. 8
★ 乘法分配律 .............................................................................................................................. 8
★ 减法的性质 .............................................................................................................................. 8
★ 除法的性质 .............................................................................................................................. 8
★ 等式 .......................................................................................................................................... 9
★ 方程 .......................................................................................................................................... 9
★ 小数 .......................................................................................................................................... 9
★ 分数 ........................................................................................................................................ 10
★ 比和比例 .................................................................................................................................11
★ 正比例和反比例 .................................................................................................................... 12
四、数量关系计算公式 ............................................................................................... 13
五、典型应用题 ............................................................................................................14
和差问题 .................................................................................................................................. 14
和倍问题 .................................................................................................................................. 14
差倍问题 .................................................................................................................................. 15
年龄问题 .................................................................................................................................. 15
植树问题 .................................................................................................................................. 15
盈亏问题 .................................................................................................................................. 16
相遇问题 .................................................................................................................................. 17
追及问题 .................................................................................................................................. 17
流水行船问题 .......................................................................................................................... 17
浓度问题 .................................................................................................................................. 17
利润与折扣问题 ...................................................................................................................... 18
百分率问题 .............................................................................................................................. 18
工程问题 .................................................................................................................................. 18
列方程解应用题 ...................................................................................................................... 19
分数、百分数应用题 .............................................................................................................. 19
比和比例应用题 ...................................................................................................................... 20
鸡兔同笼问题 .......................................................................................................................... 20
六、常用数表 ................................................................................................................21
运算定律表 ...............................................................................................................................21
常用单位换算表 .......................................................................................................................21
常用π值表 .................................................................................................................................23
100以内质数表 ........................................................................................................................23
常用小数、分数、百分数互化表 ...........................................................................................23
100以内平方表 ........................................................................................................................24
一、图形与几何
长方形
长方形的周长=(长+宽)×2
长方形的面积=长×宽
正方形
正方形的周长=边长×4
正方形的面积=边长×边长
平行四边形
平行四边形的面积=底×高 S=ah
【平行四边形面积公式的推导过程】
①把平行四边形通过剪切、平移可以转化成一个长方形。
②长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,长方
形的面积等于平行四边形的面积。
③因为:长方形面积=长×宽,所以:平行四边形面积=底×高。即:S=ah。
第 1 页 共 24 页
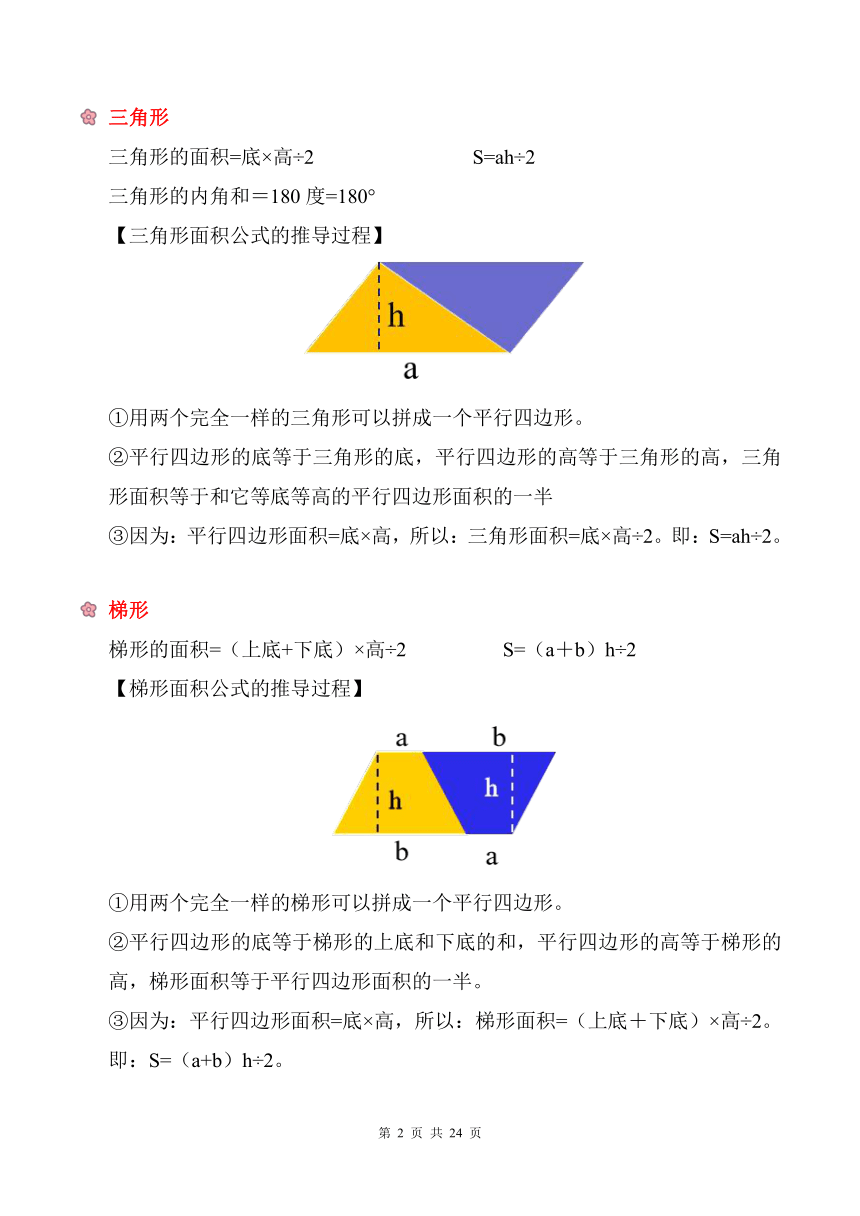
三角形
三角形的面积=底×高÷2 S=ah÷2
三角形的内角和=180度=180°
【三角形面积公式的推导过程】
①用两个完全一样的三角形可以拼成一个平行四边形。
②平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,三角
形面积等于和它等底等高的平行四边形面积的一半
③因为:平行四边形面积=底×高,所以:三角形面积=底×高÷2。即:S=ah÷2。
梯形
梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2
【梯形面积公式的推导过程】
①用两个完全一样的梯形可以拼成一个平行四边形。
②平行四边形的底等于梯形的上底和下底的和,平行四边形的高等于梯形的
高,梯形面积等于平行四边形面积的一半。
③因为:平行四边形面积=底×高,所以:梯形面积=(上底+下底)×高÷2。
即:S=(a+b)h÷2。
第 2 页 共 24 页
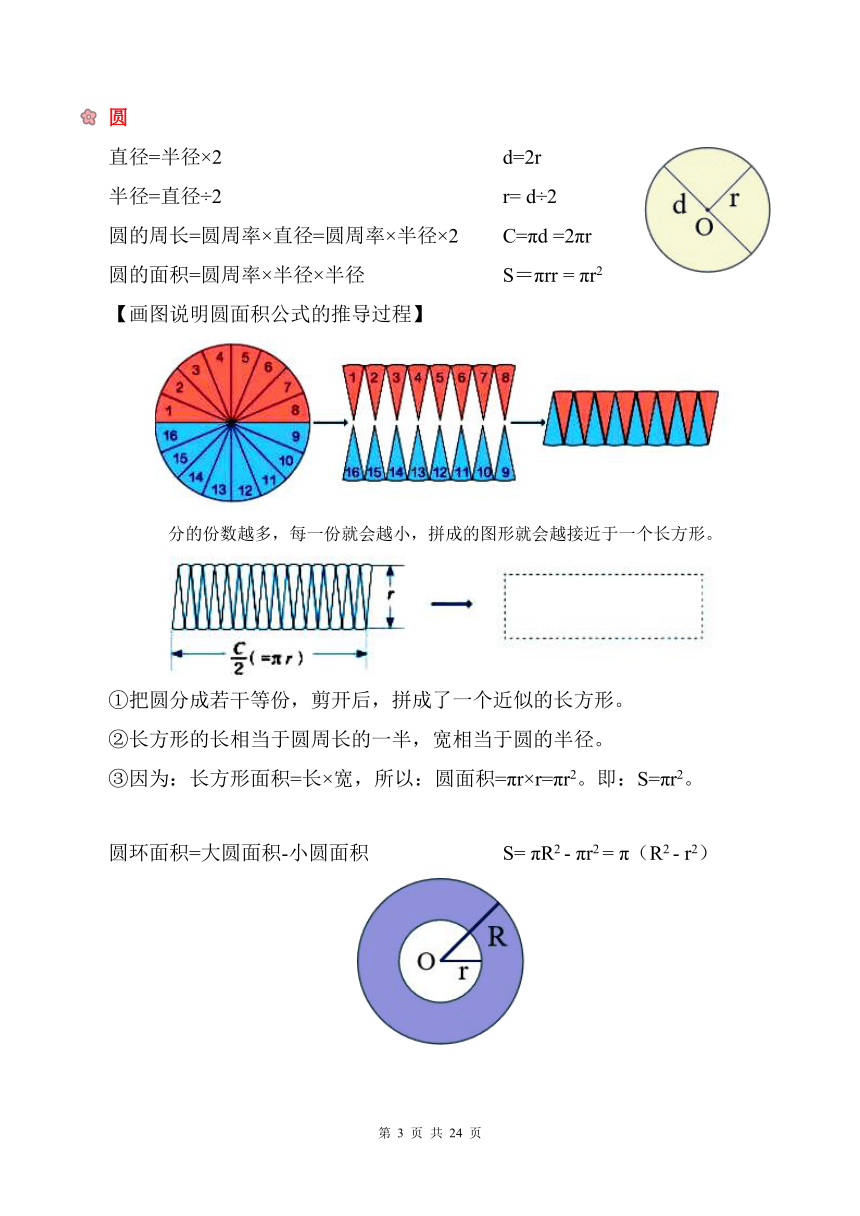
圆
直径=半径×2 d=2r
半径=直径÷2 r= d÷2
圆的周长=圆周率×直径=圆周率×半径×2 C=πd =2πr
圆的面积=圆周率×半径×半径 S=πrr = πr2
【画图说明圆面积公式的推导过程】
分的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
①把圆分成若干等份,剪开后,拼成了一个近似的长方形。
②长方形的长相当于圆周长的一半,宽相当于圆的半径。
③因为:长方形面积=长×宽,所以:圆面积=πr×r=πr2。即:S=πr2。
圆环面积=大圆面积-小圆面积 S= πR2 - πr2= π(R2 - r2)
第 3 页 共 24 页
长方体
长方体的棱长总和=(长+宽+高)×4 l = 4(a+b+h)
长方体的表面积=(长×宽+长×高+宽×高)×2 S = 2(ab+ah+bh)
长方体的体积=长×宽×高 V=abh
长方体(或正方体)的体积=底面积×高 V= S 底 h
正方体
正方体的棱长总和=棱长×12 l = 12a
正方体的表面积=棱长×棱长×6 S = 6aa=6a2
正方体的体积=棱长×棱长×棱长 V=aaa=a3
圆柱
圆柱的侧面积=底面的周长×高 S 侧=Ch=πdh=2πrh
圆柱的表面积=底面的周长×高+上下底的面积
S=Ch+2S 底 = Ch+2πrr= 2πrh +2πrr=2πr(h+r)
圆柱的体积=底面积×高 V=S 2底h = πr h
第 4 页 共 24 页
【圆柱的侧面展开后得到一个什么图形?这个图形的各部分与圆柱有何关
系?(圆柱侧面积公式的推导过程)】
①圆柱的侧面展开后一般得到一个长方形。
②长方形的长相当于圆柱的底面周长,长方形的宽相当于圆柱的高。
③因为:长方形面积=长×宽,所以:圆柱侧面积=底面周长×高。
④圆柱的侧面展开后还可能得到一个正方形。
正方形的边长=圆柱的底面周长=圆柱的高。
【我们在学习圆柱体积的计算公式时,是把圆柱转化成以前学过的一种立体
图形(近似的)进行推导的,请你说出这种立体图形的名称以及它与圆柱体
有关部分之间的关系?】
①把圆柱分成若干等份,切开后拼成了一个近似的长方体。
②长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
③因为:长方体体积=底面积×高,所以:圆柱体积=底面积×高。即:V=Sh。
圆锥
1
圆锥的体积= ×底面积×高。
3
V= 1 S 1 2
3 底
h= πr h
3
第 5 页 共 24 页
二、数的认识
名称 含义(判断方法)
0和 1、2、3……都是自然数。自然数是整数。
自然数
最小的一位数是 1,最小的自然数是 0。
“+4”读作正四。“-4”读作负四。+4也可以写成 4。
像+4、19、+8844这样的数都是正数。
正数与负数 像-4、-11、-7、-155这样的数都是负数。
0既不是正数,也不是负数。
正数都大于 0,负数都小于 0。
奇数 不能被二整除的数叫做奇数
偶数 能被二整除的数叫做偶数
一个数最小的因数是 1,最大的因数是它本身
因数
一个数的因数个数是有限的
一个数最小的倍数是它本身,没有最大的倍数
倍数
一个数的倍数个数是无限的
能被 2整除的数 个位是:0,2,4,6,8
能被 3整除的数 一各个数位上的数字的和一定是 3的倍数
能被 5整除的数 个位是:0,5
质数(素数) 一个数除了 1和它本身,不再有别的因数
合数 一个数除了 1和它本身,还有别的因数
一个合数可以写成几个素数相乘的形式,
质因数
每个素数叫做这个合数的质因数。
分解质因数 把一个合数用质因数相乘的形式表现出来叫做分解质因数
第 6 页 共 24 页
几个数公有的因数叫做这几个数的公因数,
其中最大的一个叫做这几个数的最大公因数。
最大公因数
如果两个数中,小数是大数的因数,那么小数就是这两个数
的最大公因数。
互质数 公因数只有 1的两个数叫互质数
互质数的
两个数是互质数,它们最大公因数是 1
最大公因数
几个数公有的倍数叫做这几个数的公倍数,
最小公倍数
其中最小的一个叫做最小公倍数
真分数 分子比分母小的分数叫做真分数。真分数都小于 1。
分子比分母大或者分子和分母相等的分数叫做假分数。
假分数
假分数大于或等于 1。
带分数 把假分数写成整数和真分数的形式,叫做带分数。
表示一个数是另一个数的百分之几的数,叫做百分数。
百分数
百分数也叫做百分率或百分比
把异分母分数的分别化成和原来分数相等的同分母的分数,
通分
叫做通分。(通分用最小公倍数)
把一个分数化成同它相等,但分子、分母都比较小的分数,
约分
叫做约分。(约分用最大公约数)
最简分数 分子、分母是互质数的分数,叫做最简分数。
第 7 页 共 24 页
三、算术概念
★ 加法交换律
两个数相加,交换加数的位置,它们的和不变,即 a+b=b+a。
★ 加法结合律
三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,
再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c)。
★ 乘法交换律
两个数相乘,交换因数的位置它们的积不变,即 a×b=b×a。
★ 乘法结合律
三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,
再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c)。
★ 乘法分配律
两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相
加,即(a+b)×c=a×c+b×c。
★ 减法的性质
从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变,
即 a-b-c=a-(b+c)。
★ 除法的性质
在除法里,被除数和除数同时扩大(或缩小)相同的倍数(0除外),商不变。
即 a÷b=(a÷c)÷(b÷c)或 a÷b=(a×c)÷(b×c),其中(b≠0,c≠0)。
0除以任何不是 0的数都得 0。
第 8 页 共 24 页
★ 等式
1.等号左边的数值与等号右边的数值相等的式子叫做等式。
2.等式的基本性质:
等式两边同时加上(或减去)一个相同的数,所得结果仍然是等式。
等式两边同时乘以(或除以)一个相同的数(0除外),等式仍然成立。
即如果 a=b,那么 a±c=b±c、a×c=b×c、a÷c=b÷c(0除外)。
★ 方程
1.含有未知数的等式叫方程。
2.一元一次方程:含有一个未知数,并且未知数的次数是一次的等式叫做一元
一次方程。
★ 小数
1.分母是 10、100、1000……的分数都可以用小数表示
2.一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……
3.整数和小数都是按照十进制计数法写出的数,个、十、百……以及十分之一、
百分之一……都是计数单位。每相邻两个计数单位间的进率都是 10。
4.整数和小数的数位顺序表:
第 9 页 共 24 页
5.小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。
6.小数点移动引起小数大小变化的规律:
一个小数乘 10、100、1000……只要把这个小数的小数点向右移动一位、两位、
三位……
一个小数除以 10、100、1000……只要把这个小数的小数点向左移动一位、两
位、三位……
★ 分数
1.把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数。
2.分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
3.分数大小的比较:
同分母的分数相比较,分子大的大,分子小的小。
异分母的分数相比较,先通分再比较;若分子相同,分母大的反而小。
4.分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
5.分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母,能约分的先
约分。
6.分数除以整数(0除外),等于分数乘以这个整数的倒数。
7.分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分
数的大小不变。
÷ ×
即 = (b≠0,c≠0) ÷ = (b≠0,c≠0) ×
8.一个数除以分数,等于这个数乘以分数的倒数。
9.甲数除以乙数(0除外),等于甲数乘以乙数的倒数。
第 10 页 共 24 页
★ 比和比例
1.比:两个数相除就叫做两个数的比。如:2÷5或 3:6或 1/3。
2.比的性质:比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
即 a:b=(a÷c)÷(b÷c)或 a:b=(a×c)÷(b×c),其中(b ≠0,c ≠0)。
3.比、分数、除法的关系: a÷b = a:b = (b≠0)
比 分数 除法
前项 分子 被除数
比号 分数线 除号
联系
后项 分母 除数
比值 分数值 商
区别 比表示两个数之间的关系。 分数表示一个数。 除法表示一种运算。
4.化简比:
①整数比的化简方法是:用比的前项和后项同时除以它们的最大公约数。
②小数比的化简方法是:先把小数比化成整数比,再按整数比化简方法化简。
③分数比的化简方法是:用比的前项和后项同时乘以分母的最小公倍数。
5.比例:表示两个比相等的式子。如 3:6 = 9:18
6.比例的基本性质:在比例里,两外项之积等于两内项之积。
a:b = c:d → ad = bc(b≠0,d≠0)或 = → ad=bc(b≠0,d≠0)
7.比例尺:我们把图上距离和实际距离的比叫做这幅图的比例尺。
8.比例尺=图上距离︰实际距离 比例尺 = 图上距离/ 实际距离
第 11 页 共 24 页
★ 正比例和反比例
1.正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的
量,它们的关系就叫做正比例关系。
2.反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系
就叫做反比例关系。
3.正比例与反比例的区别:
正比例 反比例
相同点 都有两种相关联的量,一种量变化,另一种量也随着变化。
商一定 积一定
不同点 y/x= k(一定) x×y=k(一定)
第 12 页 共 24 页
四、数量关系计算公式
1.和=加数+加数 和-一个加数=另一个加数
2.差=被减数-减数 被减数-差=减数 差+减数=被减数
3.因数×因数=积 积÷一个因数=另一个因数
4.被除数÷除数=商 被除数÷商=除数 商×除数=被除数
5.有余数的除法:被除数 = 商×除数+余数
6.每份数×份数=总数 总数÷每份数=份数 总数÷份数=每份数
7.1倍数×倍数=几倍数 几倍数÷1倍数=倍数 几倍数÷倍数=1倍数
8.速度×时间=路程 路程÷速度=时间 路程÷时间=速度
9.单价×数量=总价 总价÷单价=数量 总价÷数量=单价
10.工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
11.本金×利率×时间=利息
12.保险金额×保险费率×保险时间=保险费
13.应纳税收入×税率=应缴税款
第 13 页 共 24 页
五、典型应用题
和差问题
已知大小两个数的和与它们的差,求这两个数各是多少?
(和+差)÷2=大数 或 大数=和-小数
(和-差)÷2=小数 或 小数=和-大数
和倍问题
已知两个数的和与它们的倍数关系,求这两个数各是多少?
和÷(倍数+1)=小数(1倍数)
小数×倍数=大数(几倍数)
和-小数=大数
第 14 页 共 24 页
差倍问题
已知两个数的差与它们的倍数关系,求这两个数各是多少?
差÷(倍数-1)=小数(1倍数)
小数×倍数=大数(几倍数)
小数+差=大数
年龄问题
1.年龄问题的主要特点:
①两人的年龄差不变;
②两人的年龄随岁月的变化将增加或减少同一个自然数;
③两个年龄的倍数关系随年龄的增长而发生变化,年龄增大,倍数变小。
2.可以把年龄问题转化为“和差倍问题”。
植树问题
1.不封闭的植树路线:
①如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距+1
全长=株距×(株数-1)
株距=全长÷(株数-)
第 15 页 共 24 页
②如果在非封闭线路的一端要植树,另一端不要植树,那么:
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
③如果在非封闭线路的两端都不要植树,那么:
株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+)
2.封闭线路上的植树问题的数量关系如下:
株数=段数=全长一株距
全长=株距×株数
株距=全长÷株数
盈亏问题
1.把一定数量的物品分给若干对象,在两次分配方案中,一次分配的结果有剩
余即盈,一次分配的结果不足为亏。求被分配物品的数量和参加分配的人数,
这类应用题称为盈亏问题。
2.公式:
盈亏问题:(盈+亏)÷两次分配量之差=参加分配的份数
盈盈问题:(大盈一小盈)÷两次分配量之差=参加分配的份数
亏亏问题:(大亏一小亏)÷两次分配量之差=参加分配的份数
第 16 页 共 24 页
相遇问题
路程和=速度和×相遇时间
相遇时间=路程和÷速度和
速度和=路程和÷相遇时间
追及问题
路程差=速度差×追及时间
追及时间=路程差÷速度差
速度差=路程差÷追及时间
流水行船问题
1.一般公式:顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
2.两船相向航行的公式:
甲船顺水速度+乙船逆水速度=甲船静水速度+乙船静水速度
3.两船同向航行的公式:
后(前)船静水速度-前(后)船静水速度=两船距离缩小(拉大)速度
浓度问题
溶质的重量+溶剂的重量=溶液的重量
溶质的重量÷溶液的重量×100%=浓度
溶液的重量×浓度=溶质的重量
溶质的重量÷浓度=溶液的重量
第 17 页 共 24 页
利润与折扣问题
利润=售出价-成本
利润率=利润÷成本×100%=(售出价÷成本-1)×100%
涨跌金额=本金×涨跌百分比
折扣=实际售价÷原售价×100%(折扣<1)
利息=本金×利率×时间
百分率问题
发芽率=发芽种子数/试验种子数×100%
小麦的出粉率= 面粉的重量/小麦的重量×100%
产品的合格率=合格的产品数/产品总数×100%
职工的出勤率=实际出勤人数/应出勤人数×100%
工程问题
假设工作总量为“1”:
工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
甲工效+乙工效=甲、合作的工效和
工作总量÷工效和=合作时间
工效和×合作时间=工作总量
工作总量÷合作时间=工效和
第 18 页 共 24 页
列方程解应用题
列方程的步骤:
①弄清题意,确定未知数并用 x 表示;
②找出题中数量间的相等关系;
③列方程,解应用题;
④检查或验算,写出答案。
分数、百分数应用题
1.分数(百分数)应用题有三种类型。
①求一个数是另一个数的几分之几(百分之几):
从问题入手,弄清把谁看作标准的数,也就是把谁看作单位“1”谁和单位“1”
的量做比较,谁就做被除数。
②求一个数的几分之几(百分之几)是多少:
准确判断单位“1”的量,找准要求问题所对应的分率,然后根据一个数乘分
数的意义正确列式。
③已知一个数的几分之几(百分之几)是多少,求这个数:
准确判断单位“1”的量(标准量),同时找准和分率相对应的实际数量(比
较量),或找准与已知实际数量(比较量)相对应的分率。
2.公式定律:
①求一个数是另一个数的几分之几(百分之几):
比较量÷标准量=分率(百分率)
②求一个数的几分之几(百分之几)是多少:
标准量×分率(百分率)=比较量
③已知一个数的几分之几(百分之几)是多少,求这个数:
比较量÷对应分率=标准量
第 19 页 共 24 页
比和比例应用题
1.比例尺×实际距离= 图上距离
2.按比分配
①求出总份数;
②再求出各部分占总数的几分之几;
③求各部分分别是多少。
3.正、反比例
用比例解应用题,关键在于正确判断两种量是正比例关系还是反比例关系。
鸡兔同笼问题
1.这类问题可以用假设法来解决,即“假设不同为相同”,根据所做的假设,
发现实际情况出现差别,找到造成差别的原因,从而修正所做的假设,求得
正确结果。
2.公式定律:
兔数 =(实际脚数 - 每只鸡脚×鸡兔总数)÷(每只脚数 - 每只鸡脚数)
第 20 页 共 24 页
六、常用数表
运算定律表
运算定律 用字母表示
加法交换律 a+b=b+a
加法结合律 (a+b)+c=a+(b+c)
乘法交换律 a×b=b×a
乘法结合律 (a×b)×c=a×(b×c)
乘法分配律 (a+b)×c=a×c+b×c
减法运算规律 a-b-c=a-(b+c)
除法运算规律 a÷b÷c=a÷(b×c)
a÷b=(a÷c)÷(b÷c)或
除法的性质 a÷b=(a×c)÷(b×c),
其中(b≠0,c≠0)
常用单位换算表
单位 名称(符号) 换算
千米(km) 1公里=1千米
米(m) 1千米=1000米
长度 分米(dm) 1米=10分米
厘米(cm) 1分米=10厘米
毫米(mm) 1厘米=10毫米
第 21 页 共 24 页
平方千米(km2)
公顷(hm2 1平方千米=100公顷) 1公顷=10000平方米
平方米(m2)
面积 1平方米=100平方分米
平方分米(dm2)
平方厘米(cm2 1平方分米=100平方厘米)
mm2 1平方厘米=100平方毫米平方毫米( )
立方米(m3) 1立方米=1000立方分米
体积 立方分米(dm3) 1立方分米=1000立方厘米
立方厘米(cm3) 1立方厘米=1000立方毫米
L 1升=1000毫升升( )
容积 1升=1立方分米
毫升(mL) 1毫升=1立方厘米
吨(t) 1吨=1000千克
质量 千克(kg) 1千克=1000克
克(g) 1千克=1公斤=2市斤
元 1元=10角
人民币 角 1角=10分
分 1元=100分
1世纪=100年
1年=12月
年 1年=4季度
1季度=3个月
1平年=365天
平年 1闰年=366天
闰年 公历年份是 4的倍数的一般是闰年,但公历年份
是 100的倍数时,必须是 400的倍数才是闰年。
时间
大月(31天)有:1\3\5\7\8\10\12月
小月(30天)有:4\6\9\11月
月
平年 2月:28天
闰年 2月:29天
日/天 1日=24小时
时 1时=60分
分 1分=60秒
秒
第 22 页 共 24 页
常用π值表
π=3.14 8π=25.12 15π=47.1 25π=78.5
2π=6.28 9π=28.26 16π=50.24 36π=113.04
3π=9.42 10π=31.4 17π=53.38 49π=153.86
4π=12.56 11π=34.54 18π=56.52 64π=200.96
5π=15.7 12π=37.68 19π=59.66 81π=254.34
6π=18.84 13π=40.82 20π=62.8 2.25π=7.065
7π=21.98 14π=43.96 6.25π=19.625
100 以内质数表
2 3 5 7 11
13 17 19 23 29
31 37 41 43 47
53 59 61 67 71
73 79 83 89 97
常用小数、分数、百分数互化表
0.01= 1 =1% 0.06= 3 =6% 0.125= 1 =12.5% 0.5= 1 =50%
100 50 8 2
1 7 3 3
0.02= =2% 0.07= =7% 0.15= =15% 0.6= =60%
50 100 20 5
3 2 1
0.03= =3% 0.08= =8% 0.2= =20% 0.75= 3 =75%
100 25 5 4
0.04= 1 =4% 0.09= 9 =9% 0.25= 1 =25% 0.8= 4 =80%
25 100 4 5
0.05= 1 =5% 0.1= 1 =10% 0.4= 2 =40% 0.9= 9 =90%
20 10 5 10
第 23 页 共 24 页
100 以内平方表
x x2 x x2 x x2 x x2 x x2
1 1 21 441 41 1681 61 3721 81 6561
2 4 22 484 42 1764 62 3844 82 6724
3 9 23 529 43 1849 63 3969 83 6889
4 16 24 576 44 1936 64 4096 84 7056
5 25 25 625 45 2025 65 4225 85 7225
6 36 26 676 46 2116 66 4356 86 7396
7 49 27 729 47 2209 67 4489 87 7569
8 64 28 784 48 2304 68 4624 88 7744
9 81 29 841 49 2401 69 4761 89 7921
10 100 30 900 50 2500 70 4900 90 8100
11 121 31 961 51 2601 71 5041 91 8281
12 144 32 1024 52 2704 72 5184 92 8464
13 169 33 1089 53 2809 73 5329 93 8649
14 196 34 1156 54 2916 74 5476 94 8836
15 225 35 1225 55 3025 75 5625 95 9025
16 256 36 1296 56 3136 76 5776 96 9216
17 289 37 1369 57 3249 77 5929 97 9409
18 324 38 1444 58 3364 78 6084 98 9604
19 361 39 1521 59 3481 79 6241 99 9801
20 400 40 1600 60 3600 80 6400 100 10000
第 24 页 共 24 页
目 录
一、图形与几何 ..............................................................................................................1
长方形 ........................................................................................................................................ 1
正方形 ........................................................................................................................................ 1
平行四边形 ................................................................................................................................ 1
三角形 ........................................................................................................................................ 2
梯形 ............................................................................................................................................ 2
圆 ................................................................................................................................................ 3
长方体 ........................................................................................................................................ 4
正方体 ........................................................................................................................................ 4
圆柱 ............................................................................................................................................ 4
圆锥 ............................................................................................................................................ 5
二、数的认识 ..................................................................................................................6
三、算术概念 ..................................................................................................................8
★ 加法交换律 .............................................................................................................................. 8
★ 加法结合律 .............................................................................................................................. 8
★ 乘法交换律 .............................................................................................................................. 8
★ 乘法结合律 .............................................................................................................................. 8
★ 乘法分配律 .............................................................................................................................. 8
★ 减法的性质 .............................................................................................................................. 8
★ 除法的性质 .............................................................................................................................. 8
★ 等式 .......................................................................................................................................... 9
★ 方程 .......................................................................................................................................... 9
★ 小数 .......................................................................................................................................... 9
★ 分数 ........................................................................................................................................ 10
★ 比和比例 .................................................................................................................................11
★ 正比例和反比例 .................................................................................................................... 12
四、数量关系计算公式 ............................................................................................... 13
五、典型应用题 ............................................................................................................14
和差问题 .................................................................................................................................. 14
和倍问题 .................................................................................................................................. 14
差倍问题 .................................................................................................................................. 15
年龄问题 .................................................................................................................................. 15
植树问题 .................................................................................................................................. 15
盈亏问题 .................................................................................................................................. 16
相遇问题 .................................................................................................................................. 17
追及问题 .................................................................................................................................. 17
流水行船问题 .......................................................................................................................... 17
浓度问题 .................................................................................................................................. 17
利润与折扣问题 ...................................................................................................................... 18
百分率问题 .............................................................................................................................. 18
工程问题 .................................................................................................................................. 18
列方程解应用题 ...................................................................................................................... 19
分数、百分数应用题 .............................................................................................................. 19
比和比例应用题 ...................................................................................................................... 20
鸡兔同笼问题 .......................................................................................................................... 20
六、常用数表 ................................................................................................................21
运算定律表 ...............................................................................................................................21
常用单位换算表 .......................................................................................................................21
常用π值表 .................................................................................................................................23
100以内质数表 ........................................................................................................................23
常用小数、分数、百分数互化表 ...........................................................................................23
100以内平方表 ........................................................................................................................24
一、图形与几何
长方形
长方形的周长=(长+宽)×2
长方形的面积=长×宽
正方形
正方形的周长=边长×4
正方形的面积=边长×边长
平行四边形
平行四边形的面积=底×高 S=ah
【平行四边形面积公式的推导过程】
①把平行四边形通过剪切、平移可以转化成一个长方形。
②长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,长方
形的面积等于平行四边形的面积。
③因为:长方形面积=长×宽,所以:平行四边形面积=底×高。即:S=ah。
第 1 页 共 24 页
三角形
三角形的面积=底×高÷2 S=ah÷2
三角形的内角和=180度=180°
【三角形面积公式的推导过程】
①用两个完全一样的三角形可以拼成一个平行四边形。
②平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,三角
形面积等于和它等底等高的平行四边形面积的一半
③因为:平行四边形面积=底×高,所以:三角形面积=底×高÷2。即:S=ah÷2。
梯形
梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2
【梯形面积公式的推导过程】
①用两个完全一样的梯形可以拼成一个平行四边形。
②平行四边形的底等于梯形的上底和下底的和,平行四边形的高等于梯形的
高,梯形面积等于平行四边形面积的一半。
③因为:平行四边形面积=底×高,所以:梯形面积=(上底+下底)×高÷2。
即:S=(a+b)h÷2。
第 2 页 共 24 页
圆
直径=半径×2 d=2r
半径=直径÷2 r= d÷2
圆的周长=圆周率×直径=圆周率×半径×2 C=πd =2πr
圆的面积=圆周率×半径×半径 S=πrr = πr2
【画图说明圆面积公式的推导过程】
分的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
①把圆分成若干等份,剪开后,拼成了一个近似的长方形。
②长方形的长相当于圆周长的一半,宽相当于圆的半径。
③因为:长方形面积=长×宽,所以:圆面积=πr×r=πr2。即:S=πr2。
圆环面积=大圆面积-小圆面积 S= πR2 - πr2= π(R2 - r2)
第 3 页 共 24 页
长方体
长方体的棱长总和=(长+宽+高)×4 l = 4(a+b+h)
长方体的表面积=(长×宽+长×高+宽×高)×2 S = 2(ab+ah+bh)
长方体的体积=长×宽×高 V=abh
长方体(或正方体)的体积=底面积×高 V= S 底 h
正方体
正方体的棱长总和=棱长×12 l = 12a
正方体的表面积=棱长×棱长×6 S = 6aa=6a2
正方体的体积=棱长×棱长×棱长 V=aaa=a3
圆柱
圆柱的侧面积=底面的周长×高 S 侧=Ch=πdh=2πrh
圆柱的表面积=底面的周长×高+上下底的面积
S=Ch+2S 底 = Ch+2πrr= 2πrh +2πrr=2πr(h+r)
圆柱的体积=底面积×高 V=S 2底h = πr h
第 4 页 共 24 页
【圆柱的侧面展开后得到一个什么图形?这个图形的各部分与圆柱有何关
系?(圆柱侧面积公式的推导过程)】
①圆柱的侧面展开后一般得到一个长方形。
②长方形的长相当于圆柱的底面周长,长方形的宽相当于圆柱的高。
③因为:长方形面积=长×宽,所以:圆柱侧面积=底面周长×高。
④圆柱的侧面展开后还可能得到一个正方形。
正方形的边长=圆柱的底面周长=圆柱的高。
【我们在学习圆柱体积的计算公式时,是把圆柱转化成以前学过的一种立体
图形(近似的)进行推导的,请你说出这种立体图形的名称以及它与圆柱体
有关部分之间的关系?】
①把圆柱分成若干等份,切开后拼成了一个近似的长方体。
②长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
③因为:长方体体积=底面积×高,所以:圆柱体积=底面积×高。即:V=Sh。
圆锥
1
圆锥的体积= ×底面积×高。
3
V= 1 S 1 2
3 底
h= πr h
3
第 5 页 共 24 页
二、数的认识
名称 含义(判断方法)
0和 1、2、3……都是自然数。自然数是整数。
自然数
最小的一位数是 1,最小的自然数是 0。
“+4”读作正四。“-4”读作负四。+4也可以写成 4。
像+4、19、+8844这样的数都是正数。
正数与负数 像-4、-11、-7、-155这样的数都是负数。
0既不是正数,也不是负数。
正数都大于 0,负数都小于 0。
奇数 不能被二整除的数叫做奇数
偶数 能被二整除的数叫做偶数
一个数最小的因数是 1,最大的因数是它本身
因数
一个数的因数个数是有限的
一个数最小的倍数是它本身,没有最大的倍数
倍数
一个数的倍数个数是无限的
能被 2整除的数 个位是:0,2,4,6,8
能被 3整除的数 一各个数位上的数字的和一定是 3的倍数
能被 5整除的数 个位是:0,5
质数(素数) 一个数除了 1和它本身,不再有别的因数
合数 一个数除了 1和它本身,还有别的因数
一个合数可以写成几个素数相乘的形式,
质因数
每个素数叫做这个合数的质因数。
分解质因数 把一个合数用质因数相乘的形式表现出来叫做分解质因数
第 6 页 共 24 页
几个数公有的因数叫做这几个数的公因数,
其中最大的一个叫做这几个数的最大公因数。
最大公因数
如果两个数中,小数是大数的因数,那么小数就是这两个数
的最大公因数。
互质数 公因数只有 1的两个数叫互质数
互质数的
两个数是互质数,它们最大公因数是 1
最大公因数
几个数公有的倍数叫做这几个数的公倍数,
最小公倍数
其中最小的一个叫做最小公倍数
真分数 分子比分母小的分数叫做真分数。真分数都小于 1。
分子比分母大或者分子和分母相等的分数叫做假分数。
假分数
假分数大于或等于 1。
带分数 把假分数写成整数和真分数的形式,叫做带分数。
表示一个数是另一个数的百分之几的数,叫做百分数。
百分数
百分数也叫做百分率或百分比
把异分母分数的分别化成和原来分数相等的同分母的分数,
通分
叫做通分。(通分用最小公倍数)
把一个分数化成同它相等,但分子、分母都比较小的分数,
约分
叫做约分。(约分用最大公约数)
最简分数 分子、分母是互质数的分数,叫做最简分数。
第 7 页 共 24 页
三、算术概念
★ 加法交换律
两个数相加,交换加数的位置,它们的和不变,即 a+b=b+a。
★ 加法结合律
三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,
再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c)。
★ 乘法交换律
两个数相乘,交换因数的位置它们的积不变,即 a×b=b×a。
★ 乘法结合律
三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,
再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c)。
★ 乘法分配律
两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相
加,即(a+b)×c=a×c+b×c。
★ 减法的性质
从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变,
即 a-b-c=a-(b+c)。
★ 除法的性质
在除法里,被除数和除数同时扩大(或缩小)相同的倍数(0除外),商不变。
即 a÷b=(a÷c)÷(b÷c)或 a÷b=(a×c)÷(b×c),其中(b≠0,c≠0)。
0除以任何不是 0的数都得 0。
第 8 页 共 24 页
★ 等式
1.等号左边的数值与等号右边的数值相等的式子叫做等式。
2.等式的基本性质:
等式两边同时加上(或减去)一个相同的数,所得结果仍然是等式。
等式两边同时乘以(或除以)一个相同的数(0除外),等式仍然成立。
即如果 a=b,那么 a±c=b±c、a×c=b×c、a÷c=b÷c(0除外)。
★ 方程
1.含有未知数的等式叫方程。
2.一元一次方程:含有一个未知数,并且未知数的次数是一次的等式叫做一元
一次方程。
★ 小数
1.分母是 10、100、1000……的分数都可以用小数表示
2.一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……
3.整数和小数都是按照十进制计数法写出的数,个、十、百……以及十分之一、
百分之一……都是计数单位。每相邻两个计数单位间的进率都是 10。
4.整数和小数的数位顺序表:
第 9 页 共 24 页
5.小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。
6.小数点移动引起小数大小变化的规律:
一个小数乘 10、100、1000……只要把这个小数的小数点向右移动一位、两位、
三位……
一个小数除以 10、100、1000……只要把这个小数的小数点向左移动一位、两
位、三位……
★ 分数
1.把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数。
2.分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
3.分数大小的比较:
同分母的分数相比较,分子大的大,分子小的小。
异分母的分数相比较,先通分再比较;若分子相同,分母大的反而小。
4.分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
5.分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母,能约分的先
约分。
6.分数除以整数(0除外),等于分数乘以这个整数的倒数。
7.分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分
数的大小不变。
÷ ×
即 = (b≠0,c≠0) ÷ = (b≠0,c≠0) ×
8.一个数除以分数,等于这个数乘以分数的倒数。
9.甲数除以乙数(0除外),等于甲数乘以乙数的倒数。
第 10 页 共 24 页
★ 比和比例
1.比:两个数相除就叫做两个数的比。如:2÷5或 3:6或 1/3。
2.比的性质:比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
即 a:b=(a÷c)÷(b÷c)或 a:b=(a×c)÷(b×c),其中(b ≠0,c ≠0)。
3.比、分数、除法的关系: a÷b = a:b = (b≠0)
比 分数 除法
前项 分子 被除数
比号 分数线 除号
联系
后项 分母 除数
比值 分数值 商
区别 比表示两个数之间的关系。 分数表示一个数。 除法表示一种运算。
4.化简比:
①整数比的化简方法是:用比的前项和后项同时除以它们的最大公约数。
②小数比的化简方法是:先把小数比化成整数比,再按整数比化简方法化简。
③分数比的化简方法是:用比的前项和后项同时乘以分母的最小公倍数。
5.比例:表示两个比相等的式子。如 3:6 = 9:18
6.比例的基本性质:在比例里,两外项之积等于两内项之积。
a:b = c:d → ad = bc(b≠0,d≠0)或 = → ad=bc(b≠0,d≠0)
7.比例尺:我们把图上距离和实际距离的比叫做这幅图的比例尺。
8.比例尺=图上距离︰实际距离 比例尺 = 图上距离/ 实际距离
第 11 页 共 24 页
★ 正比例和反比例
1.正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的
量,它们的关系就叫做正比例关系。
2.反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系
就叫做反比例关系。
3.正比例与反比例的区别:
正比例 反比例
相同点 都有两种相关联的量,一种量变化,另一种量也随着变化。
商一定 积一定
不同点 y/x= k(一定) x×y=k(一定)
第 12 页 共 24 页
四、数量关系计算公式
1.和=加数+加数 和-一个加数=另一个加数
2.差=被减数-减数 被减数-差=减数 差+减数=被减数
3.因数×因数=积 积÷一个因数=另一个因数
4.被除数÷除数=商 被除数÷商=除数 商×除数=被除数
5.有余数的除法:被除数 = 商×除数+余数
6.每份数×份数=总数 总数÷每份数=份数 总数÷份数=每份数
7.1倍数×倍数=几倍数 几倍数÷1倍数=倍数 几倍数÷倍数=1倍数
8.速度×时间=路程 路程÷速度=时间 路程÷时间=速度
9.单价×数量=总价 总价÷单价=数量 总价÷数量=单价
10.工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
11.本金×利率×时间=利息
12.保险金额×保险费率×保险时间=保险费
13.应纳税收入×税率=应缴税款
第 13 页 共 24 页
五、典型应用题
和差问题
已知大小两个数的和与它们的差,求这两个数各是多少?
(和+差)÷2=大数 或 大数=和-小数
(和-差)÷2=小数 或 小数=和-大数
和倍问题
已知两个数的和与它们的倍数关系,求这两个数各是多少?
和÷(倍数+1)=小数(1倍数)
小数×倍数=大数(几倍数)
和-小数=大数
第 14 页 共 24 页
差倍问题
已知两个数的差与它们的倍数关系,求这两个数各是多少?
差÷(倍数-1)=小数(1倍数)
小数×倍数=大数(几倍数)
小数+差=大数
年龄问题
1.年龄问题的主要特点:
①两人的年龄差不变;
②两人的年龄随岁月的变化将增加或减少同一个自然数;
③两个年龄的倍数关系随年龄的增长而发生变化,年龄增大,倍数变小。
2.可以把年龄问题转化为“和差倍问题”。
植树问题
1.不封闭的植树路线:
①如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距+1
全长=株距×(株数-1)
株距=全长÷(株数-)
第 15 页 共 24 页
②如果在非封闭线路的一端要植树,另一端不要植树,那么:
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
③如果在非封闭线路的两端都不要植树,那么:
株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+)
2.封闭线路上的植树问题的数量关系如下:
株数=段数=全长一株距
全长=株距×株数
株距=全长÷株数
盈亏问题
1.把一定数量的物品分给若干对象,在两次分配方案中,一次分配的结果有剩
余即盈,一次分配的结果不足为亏。求被分配物品的数量和参加分配的人数,
这类应用题称为盈亏问题。
2.公式:
盈亏问题:(盈+亏)÷两次分配量之差=参加分配的份数
盈盈问题:(大盈一小盈)÷两次分配量之差=参加分配的份数
亏亏问题:(大亏一小亏)÷两次分配量之差=参加分配的份数
第 16 页 共 24 页
相遇问题
路程和=速度和×相遇时间
相遇时间=路程和÷速度和
速度和=路程和÷相遇时间
追及问题
路程差=速度差×追及时间
追及时间=路程差÷速度差
速度差=路程差÷追及时间
流水行船问题
1.一般公式:顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
2.两船相向航行的公式:
甲船顺水速度+乙船逆水速度=甲船静水速度+乙船静水速度
3.两船同向航行的公式:
后(前)船静水速度-前(后)船静水速度=两船距离缩小(拉大)速度
浓度问题
溶质的重量+溶剂的重量=溶液的重量
溶质的重量÷溶液的重量×100%=浓度
溶液的重量×浓度=溶质的重量
溶质的重量÷浓度=溶液的重量
第 17 页 共 24 页
利润与折扣问题
利润=售出价-成本
利润率=利润÷成本×100%=(售出价÷成本-1)×100%
涨跌金额=本金×涨跌百分比
折扣=实际售价÷原售价×100%(折扣<1)
利息=本金×利率×时间
百分率问题
发芽率=发芽种子数/试验种子数×100%
小麦的出粉率= 面粉的重量/小麦的重量×100%
产品的合格率=合格的产品数/产品总数×100%
职工的出勤率=实际出勤人数/应出勤人数×100%
工程问题
假设工作总量为“1”:
工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
甲工效+乙工效=甲、合作的工效和
工作总量÷工效和=合作时间
工效和×合作时间=工作总量
工作总量÷合作时间=工效和
第 18 页 共 24 页
列方程解应用题
列方程的步骤:
①弄清题意,确定未知数并用 x 表示;
②找出题中数量间的相等关系;
③列方程,解应用题;
④检查或验算,写出答案。
分数、百分数应用题
1.分数(百分数)应用题有三种类型。
①求一个数是另一个数的几分之几(百分之几):
从问题入手,弄清把谁看作标准的数,也就是把谁看作单位“1”谁和单位“1”
的量做比较,谁就做被除数。
②求一个数的几分之几(百分之几)是多少:
准确判断单位“1”的量,找准要求问题所对应的分率,然后根据一个数乘分
数的意义正确列式。
③已知一个数的几分之几(百分之几)是多少,求这个数:
准确判断单位“1”的量(标准量),同时找准和分率相对应的实际数量(比
较量),或找准与已知实际数量(比较量)相对应的分率。
2.公式定律:
①求一个数是另一个数的几分之几(百分之几):
比较量÷标准量=分率(百分率)
②求一个数的几分之几(百分之几)是多少:
标准量×分率(百分率)=比较量
③已知一个数的几分之几(百分之几)是多少,求这个数:
比较量÷对应分率=标准量
第 19 页 共 24 页
比和比例应用题
1.比例尺×实际距离= 图上距离
2.按比分配
①求出总份数;
②再求出各部分占总数的几分之几;
③求各部分分别是多少。
3.正、反比例
用比例解应用题,关键在于正确判断两种量是正比例关系还是反比例关系。
鸡兔同笼问题
1.这类问题可以用假设法来解决,即“假设不同为相同”,根据所做的假设,
发现实际情况出现差别,找到造成差别的原因,从而修正所做的假设,求得
正确结果。
2.公式定律:
兔数 =(实际脚数 - 每只鸡脚×鸡兔总数)÷(每只脚数 - 每只鸡脚数)
第 20 页 共 24 页
六、常用数表
运算定律表
运算定律 用字母表示
加法交换律 a+b=b+a
加法结合律 (a+b)+c=a+(b+c)
乘法交换律 a×b=b×a
乘法结合律 (a×b)×c=a×(b×c)
乘法分配律 (a+b)×c=a×c+b×c
减法运算规律 a-b-c=a-(b+c)
除法运算规律 a÷b÷c=a÷(b×c)
a÷b=(a÷c)÷(b÷c)或
除法的性质 a÷b=(a×c)÷(b×c),
其中(b≠0,c≠0)
常用单位换算表
单位 名称(符号) 换算
千米(km) 1公里=1千米
米(m) 1千米=1000米
长度 分米(dm) 1米=10分米
厘米(cm) 1分米=10厘米
毫米(mm) 1厘米=10毫米
第 21 页 共 24 页
平方千米(km2)
公顷(hm2 1平方千米=100公顷) 1公顷=10000平方米
平方米(m2)
面积 1平方米=100平方分米
平方分米(dm2)
平方厘米(cm2 1平方分米=100平方厘米)
mm2 1平方厘米=100平方毫米平方毫米( )
立方米(m3) 1立方米=1000立方分米
体积 立方分米(dm3) 1立方分米=1000立方厘米
立方厘米(cm3) 1立方厘米=1000立方毫米
L 1升=1000毫升升( )
容积 1升=1立方分米
毫升(mL) 1毫升=1立方厘米
吨(t) 1吨=1000千克
质量 千克(kg) 1千克=1000克
克(g) 1千克=1公斤=2市斤
元 1元=10角
人民币 角 1角=10分
分 1元=100分
1世纪=100年
1年=12月
年 1年=4季度
1季度=3个月
1平年=365天
平年 1闰年=366天
闰年 公历年份是 4的倍数的一般是闰年,但公历年份
是 100的倍数时,必须是 400的倍数才是闰年。
时间
大月(31天)有:1\3\5\7\8\10\12月
小月(30天)有:4\6\9\11月
月
平年 2月:28天
闰年 2月:29天
日/天 1日=24小时
时 1时=60分
分 1分=60秒
秒
第 22 页 共 24 页
常用π值表
π=3.14 8π=25.12 15π=47.1 25π=78.5
2π=6.28 9π=28.26 16π=50.24 36π=113.04
3π=9.42 10π=31.4 17π=53.38 49π=153.86
4π=12.56 11π=34.54 18π=56.52 64π=200.96
5π=15.7 12π=37.68 19π=59.66 81π=254.34
6π=18.84 13π=40.82 20π=62.8 2.25π=7.065
7π=21.98 14π=43.96 6.25π=19.625
100 以内质数表
2 3 5 7 11
13 17 19 23 29
31 37 41 43 47
53 59 61 67 71
73 79 83 89 97
常用小数、分数、百分数互化表
0.01= 1 =1% 0.06= 3 =6% 0.125= 1 =12.5% 0.5= 1 =50%
100 50 8 2
1 7 3 3
0.02= =2% 0.07= =7% 0.15= =15% 0.6= =60%
50 100 20 5
3 2 1
0.03= =3% 0.08= =8% 0.2= =20% 0.75= 3 =75%
100 25 5 4
0.04= 1 =4% 0.09= 9 =9% 0.25= 1 =25% 0.8= 4 =80%
25 100 4 5
0.05= 1 =5% 0.1= 1 =10% 0.4= 2 =40% 0.9= 9 =90%
20 10 5 10
第 23 页 共 24 页
100 以内平方表
x x2 x x2 x x2 x x2 x x2
1 1 21 441 41 1681 61 3721 81 6561
2 4 22 484 42 1764 62 3844 82 6724
3 9 23 529 43 1849 63 3969 83 6889
4 16 24 576 44 1936 64 4096 84 7056
5 25 25 625 45 2025 65 4225 85 7225
6 36 26 676 46 2116 66 4356 86 7396
7 49 27 729 47 2209 67 4489 87 7569
8 64 28 784 48 2304 68 4624 88 7744
9 81 29 841 49 2401 69 4761 89 7921
10 100 30 900 50 2500 70 4900 90 8100
11 121 31 961 51 2601 71 5041 91 8281
12 144 32 1024 52 2704 72 5184 92 8464
13 169 33 1089 53 2809 73 5329 93 8649
14 196 34 1156 54 2916 74 5476 94 8836
15 225 35 1225 55 3025 75 5625 95 9025
16 256 36 1296 56 3136 76 5776 96 9216
17 289 37 1369 57 3249 77 5929 97 9409
18 324 38 1444 58 3364 78 6084 98 9604
19 361 39 1521 59 3481 79 6241 99 9801
20 400 40 1600 60 3600 80 6400 100 10000
第 24 页 共 24 页
同课章节目录
