八年级数学(华师大版)下册教学课件:17.2.1平面直角坐标(共19张PPT)
文档属性
| 名称 | 八年级数学(华师大版)下册教学课件:17.2.1平面直角坐标(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 498.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-25 07:29:39 | ||
图片预览






文档简介
课件19张PPT。
选自《华东师大版教材数学八年级下册》
&17.2.1 平面直角坐标系勒内·笛卡尔 :
法国著名的哲学家、数学家、物理学家。
因将几何坐标系公式化而被称为“解析几何”之父。我思故我在 我思故我在1、知识与技能
通过例子让学生感受和理解平面直角坐标系等相关概念,了解平面直角坐标系中点的坐标的特点,会求点的对称点的坐标。
2、方法和人生价值观
通过实例感知平面直角坐标系的特征,渗透数形结合思想、对应思想,了解事物是相互联系的,培养学生辩证唯物主义观。
学习目标:重点:
平面直角坐标系及其相关概念。
难点:点的坐标的理解。重点、难点实际问题一:
一天,小米的朋友来我校找红米有事,走到苏宁电器门口(鹤煤大道与华夏南路交叉口),请你帮红米描述一下我校的位置,以便小米快速找到。 (图中福田中学即为我校,离鹤煤大道500米,华夏南路1000米)如图情境引入表述:
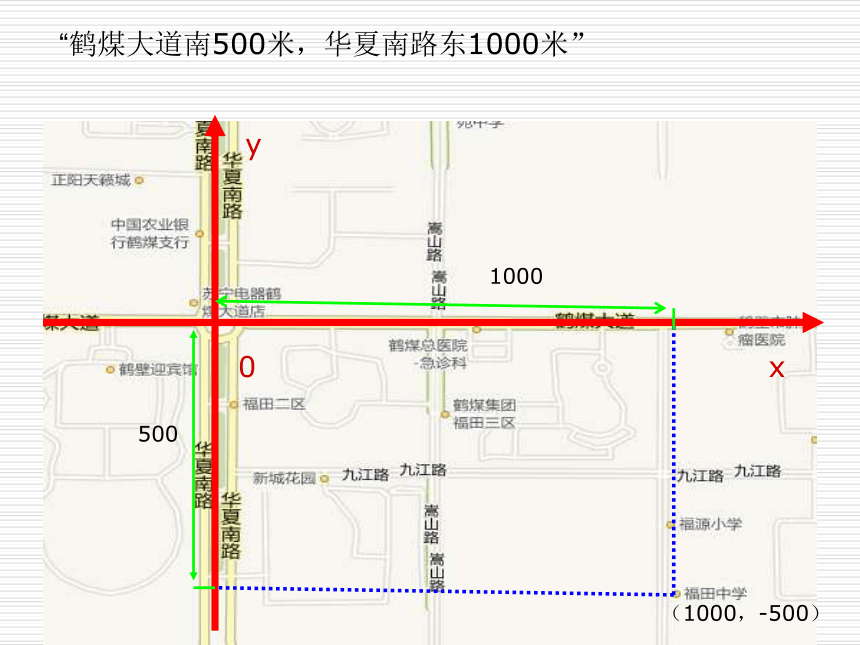
“鹤煤大道南500米,华夏南路东1000米”思考:
类似利用数轴上的实数来表示直线上的点,能否找到一种方法来表示平面内点的位置呢?0xy“鹤煤大道南500米,华夏南路东1000米”1000500(1000,-500)平面直角坐标系:
在平面上有公共原点、互相垂直且有相同单位长度的两条数轴,构成平面直角坐标系。
坐标是一对有序实数Ⅱ(-,+)Ⅲ(-,-)Ⅳ(+,-)Ⅰ(+,+)新知探究一、平面上点与有序实数对的关系1、在平面直角坐标系中,有序实数对(a,b)描述的是一个点 P 的位置,该如何确定点 P 的位置呢?
2、已知平面内一点Q,你能确定与它相应的一对有序实数(m,n)吗?
新知探究二、 在平面直角坐标系中,有序实数对(a,b)描述的是一个点 P 的位置,该如何确定点 P 的位置呢?yo-11-11ab P 过 x 轴上表示 a的点作 x 轴的垂线,再过 y 轴上表示 b 的点作 y 轴的垂线,两线的交点即为点 P .xxyo-11-11mn Q 如图,已知平面内一点Q,你能确定与它相应的一对有序实数(m,n)吗?(m,n) 过点 Q 分别作 x 轴,y 轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点 Q 的坐标,可表示为 Q(m,n).yo-123456789-2-3-4-5-6-7-8-9112345-1-2-3-4-5A(4,1)B(-1,4)CD例1 在直角坐标系中,描出下列各点的位置:
A(4,1),B(-1,4),C(-4,-2),D(3,-2),
E(0,1 ),F( -4,0 ) .并指出各点所在的象限。x(-4,-2)(3,-2)yo-123456789-2-3-4-5-6-7-8-9112345-1-2-3-4-5例 2 写出图中点A、B、C 的坐标. x.A..BC(-4,3)(-3,-2)(1 ,-3)合作探究: 请小组合作探讨下面特殊位置的点的坐标特征。坐标轴上点的坐标特征?
原点坐标的特征?
点 与点 关于x轴对称,问其坐标的关系?若关于y轴对称,其坐标关系如何?若关于原点对称哪?1、分别请写出点(3,4)关于原点,x轴,y轴的对称点。
2、点(6,0)在那个位置?探究检测一、判断:
1.对于坐标平面内的任一点,都有唯 一的一对有序实数与它对应.( )
2.在直角坐标系内,原点的坐标是0.()
3.点 A(a ,-b )在第二象限,则点B(-a , b )在第四象限. ( )
4.若点 P 的坐标为(a,b),且 a·b =0,则点 P 一定在坐标原点. ( )答案:√ × × ×当堂练习二、已知 P 点坐标为(2 a + 1,a-3)
( 1 ) 点 P 在 x 轴上,则 a= ;
( 2 ) 点 P 在 y 轴上,则 a= ;
三、若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 .3(5,-4)当堂练习小结与反思4.在学习过程中你还存在哪些问题? 1、P41 习题17.2 第2题
2、请你上网查有关坐标系的形成历史过程及现实生活中应用坐标系的例子。
3、请大家预习函数图象作 业
选自《华东师大版教材数学八年级下册》
&17.2.1 平面直角坐标系勒内·笛卡尔 :
法国著名的哲学家、数学家、物理学家。
因将几何坐标系公式化而被称为“解析几何”之父。我思故我在 我思故我在1、知识与技能
通过例子让学生感受和理解平面直角坐标系等相关概念,了解平面直角坐标系中点的坐标的特点,会求点的对称点的坐标。
2、方法和人生价值观
通过实例感知平面直角坐标系的特征,渗透数形结合思想、对应思想,了解事物是相互联系的,培养学生辩证唯物主义观。
学习目标:重点:
平面直角坐标系及其相关概念。
难点:点的坐标的理解。重点、难点实际问题一:
一天,小米的朋友来我校找红米有事,走到苏宁电器门口(鹤煤大道与华夏南路交叉口),请你帮红米描述一下我校的位置,以便小米快速找到。 (图中福田中学即为我校,离鹤煤大道500米,华夏南路1000米)如图情境引入表述:
“鹤煤大道南500米,华夏南路东1000米”思考:
类似利用数轴上的实数来表示直线上的点,能否找到一种方法来表示平面内点的位置呢?0xy“鹤煤大道南500米,华夏南路东1000米”1000500(1000,-500)平面直角坐标系:
在平面上有公共原点、互相垂直且有相同单位长度的两条数轴,构成平面直角坐标系。
坐标是一对有序实数Ⅱ(-,+)Ⅲ(-,-)Ⅳ(+,-)Ⅰ(+,+)新知探究一、平面上点与有序实数对的关系1、在平面直角坐标系中,有序实数对(a,b)描述的是一个点 P 的位置,该如何确定点 P 的位置呢?
2、已知平面内一点Q,你能确定与它相应的一对有序实数(m,n)吗?
新知探究二、 在平面直角坐标系中,有序实数对(a,b)描述的是一个点 P 的位置,该如何确定点 P 的位置呢?yo-11-11ab P 过 x 轴上表示 a的点作 x 轴的垂线,再过 y 轴上表示 b 的点作 y 轴的垂线,两线的交点即为点 P .xxyo-11-11mn Q 如图,已知平面内一点Q,你能确定与它相应的一对有序实数(m,n)吗?(m,n) 过点 Q 分别作 x 轴,y 轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点 Q 的坐标,可表示为 Q(m,n).yo-123456789-2-3-4-5-6-7-8-9112345-1-2-3-4-5A(4,1)B(-1,4)CD例1 在直角坐标系中,描出下列各点的位置:
A(4,1),B(-1,4),C(-4,-2),D(3,-2),
E(0,1 ),F( -4,0 ) .并指出各点所在的象限。x(-4,-2)(3,-2)yo-123456789-2-3-4-5-6-7-8-9112345-1-2-3-4-5例 2 写出图中点A、B、C 的坐标. x.A..BC(-4,3)(-3,-2)(1 ,-3)合作探究: 请小组合作探讨下面特殊位置的点的坐标特征。坐标轴上点的坐标特征?
原点坐标的特征?
点 与点 关于x轴对称,问其坐标的关系?若关于y轴对称,其坐标关系如何?若关于原点对称哪?1、分别请写出点(3,4)关于原点,x轴,y轴的对称点。
2、点(6,0)在那个位置?探究检测一、判断:
1.对于坐标平面内的任一点,都有唯 一的一对有序实数与它对应.( )
2.在直角坐标系内,原点的坐标是0.()
3.点 A(a ,-b )在第二象限,则点B(-a , b )在第四象限. ( )
4.若点 P 的坐标为(a,b),且 a·b =0,则点 P 一定在坐标原点. ( )答案:√ × × ×当堂练习二、已知 P 点坐标为(2 a + 1,a-3)
( 1 ) 点 P 在 x 轴上,则 a= ;
( 2 ) 点 P 在 y 轴上,则 a= ;
三、若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 .3(5,-4)当堂练习小结与反思4.在学习过程中你还存在哪些问题? 1、P41 习题17.2 第2题
2、请你上网查有关坐标系的形成历史过程及现实生活中应用坐标系的例子。
3、请大家预习函数图象作 业
