小学数学北师大版(2024)五年级下册七 邮票的张数课件(共18张PPT)
文档属性
| 名称 | 小学数学北师大版(2024)五年级下册七 邮票的张数课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第1课时 邮票的张数
北师版数学五年级下册课件
七 用方程解决问题
情境导入
猜谜语
不大不大,
浑身净画,
背个纸口袋,
走遍天下。 (打一物)
谜底:邮票
邮票承载着美丽和历史,它具有观赏和收藏的价值,不少人有收集邮票的爱好。今天我们的新知识就和邮票有关,开启今天的学习吧!
探索新知
探究点 解形如“ax±x=b”的方程
你能说一说图上告诉我们哪些信息?
根据这些信息你能提出什么数学问题?
姐姐和弟弟各有多少张邮票?
探究新知
弟弟和姐姐各有多少张邮票?尝试用方程解决。
用方程求弟弟和姐姐各有多少张邮票,需要找出题中的等量关系,根据等量关系列方程解答
弟弟和姐姐的邮票张数都不知道,怎么办呢?
等量关系:
合作探究
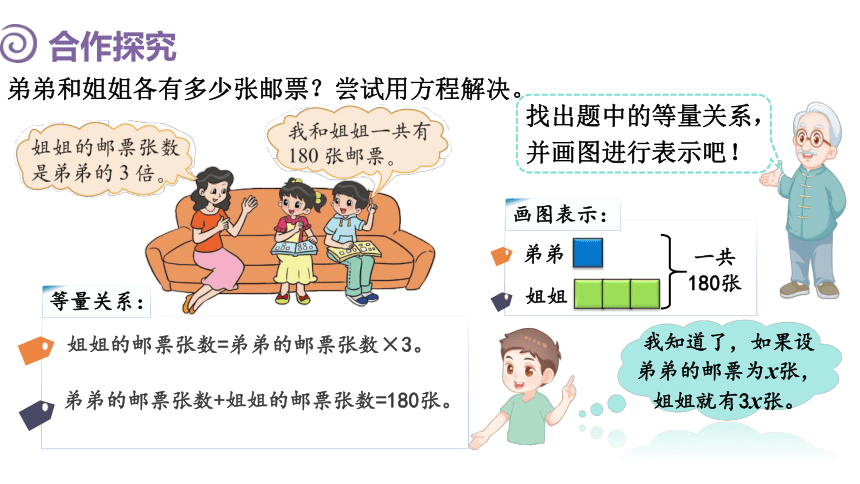
弟弟和姐姐各有多少张邮票?尝试用方程解决。
姐姐的邮票张数=弟弟的邮票张数×3。
弟弟的邮票张数+姐姐的邮票张数=180张。
画图表示:
弟弟
姐姐
一共180张
我知道了,如果设弟弟的邮票为x张,姐姐就有3x张。
找出题中的等量关系,并画图进行表示吧!
探究新知
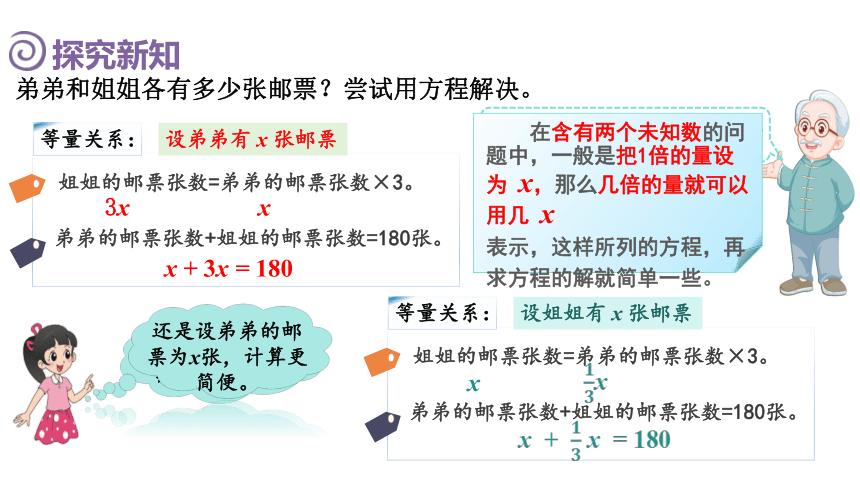
等量关系:
姐姐的邮票张数=弟弟的邮票张数×3。
弟弟的邮票张数+姐姐的邮票张数=180张。
x
3x
x + 3x = 180
大家还有不同的想法吗?
设弟弟有 x 张邮票
弟弟和姐姐各有多少张邮票?尝试用方程解决。
如果设姐姐的邮票为x张.....
等量关系:
姐姐的邮票张数=弟弟的邮票张数×3。
弟弟的邮票张数+姐姐的邮票张数=180张。
x
x
x + x = 180
设姐姐有 x 张邮票
还是设弟弟的邮票为x张,计算更简便。
在含有两个未知数的问题中,一般是把1倍的量设为 x,那么几倍的量就可以用几 x
表示,这样所列的方程,再求方程的解就简单一些。
x + 3x = 180
探索新知
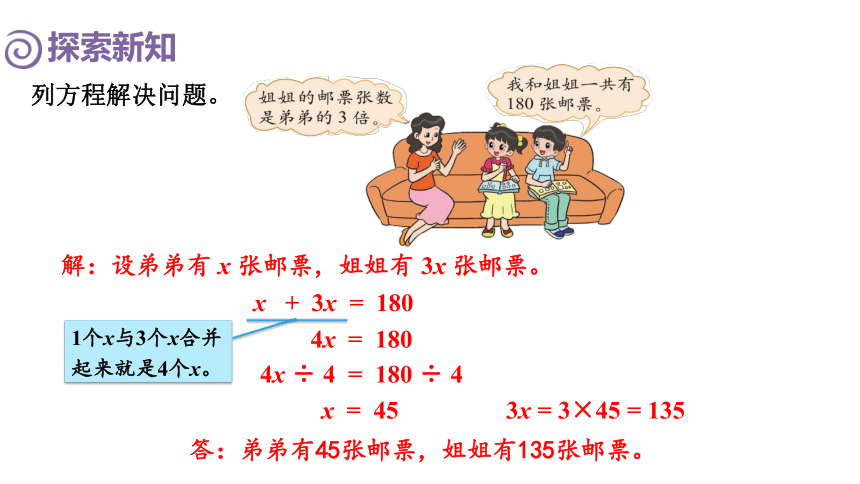
列方程解决问题。
解:设弟弟有 x 张邮票,姐姐有 3x 张邮票。
答:弟弟有45张邮票,姐姐有135张邮票。
4x = 180
x = 45
3x = 3×45 = 135
4x ÷ 4 = 180 ÷ 4
1个x与3个x合并起来就是4个x。
探索新知
如果把“我和姐姐一共有180张邮票”改为“姐姐比我多90张邮票”,可以怎样列方程呢?
姐姐比我多90 张邮票。
等量关系:
姐姐的邮票张数=弟弟的邮票张数×3。
姐姐的邮票张数-弟弟的邮票张数=90张。
我们还是先来写等量关系式,画示意图。
画图表示:
弟弟
姐姐
90张
设弟弟有 x 张邮票,
x
3x
3x - x = 90
探索新知
弟弟和姐姐各有多少张邮票?列方程解决问题。
解:设弟弟有x张邮票,姐姐有3x张邮票。
答:弟弟有45张邮票,姐姐有135张邮票。
3x - x = 90
2x = 90
x = 45
3x = 3×45 = 135
2x ÷ 2 = 90 ÷ 2
3个x减去1个x是2个x。
探索新知
小试牛刀
源自“典中点”精选题库
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,箱子中的乒乓球没有了,羽毛球还有6个。一共取了几次?取出的乒乓球和羽毛球分别有多少个?
解:设一共取了x次。
5x-3x=6
x=3 3×5=15(个) 3×3=9(个)
答:一共取了3次,取出的乒乓球有15个,取出的羽毛球有9个。
当堂练习
源于教材P70页“练一练”
1. 根据下面题中的信息写出等量关系,再列方程解决问题。
⑴ 这幅画的长、宽各是多少厘米?
解:设宽为x cm,长为2x cm。
(x+2x)×2 = 162
3x×2÷2 = 162÷2
3x÷3 = 81÷3
x = 27
长:2x = 2×27 = 54
答:这幅画的长是54厘米,宽是27厘米。
长=宽×2
(长+宽)×2=162
等量关系:
当堂练习
源于教材P70页“练一练”
1. 根据下面题中的信息写出等量关系,再列方程解决问题。
⑵ 白键和黑键各有多少?
白键个数+黑键个数=88
白键个数-黑键个数=16
等量关系:
解:设黑键有 x 个,白键有(x+16)个。
x + 16 + x = 88
2x+ 16 -16 = 88-16
2x÷2 = 72÷2
x = 36
白键:x+16 = 36+16 = 52
答:黑键有36个,白键有52个。
当堂练习
源于教材P70页“练一练”
解:设小丽今年x岁。
3x + 4 = 37
3x - 4 = 37 - 4
3x = 33
x = 11
答:小丽今年11岁。
小丽的年龄×3 + 4 = 妈妈的年龄
等量关系:
3x÷3 = 33÷3
2. 妈妈的年龄比小丽年龄的3倍多4岁,妈妈今年37岁,小丽今年几岁?列方程解决问题。
当堂练习
源于教材P70页“练一练”
3. 平均每盘有几个橘子?
解:设平均每盘有 x 个橘子。
4x + 2 = 50
4x + 2 - 2 = 50 - 2
4x = 48
x = 12
平均每盘橘子数量×4 + 2 = 橘子总数
答:平均每盘有 12 个橘子。
等量关系:
4x÷4 = 48÷4
4.如图,正方形的周长比等边三角形的周长多 5 cm,正方形和三角形周长各是多少厘米?
当堂练习
源于教材P70页“练一练”
4x
3x
4x - 3x = 5
x = 5
正方形:4x = 4×5 = 20
三角形:3x = 3×5 = 15
解:正方形的边长是 x cm,
等边三角形的边长也是 x cm。
答:正方形周长20厘米,三角形周长15厘米。
5.
当堂练习
源于教材P70页“练一练”
如果它们都在生长旺盛期,开始时竹子高32cm,钟状菌高0.5cm。几时后钟状菌的高度能赶上竹子?先说一说等量关系,再列方程解决。
钟状菌开始时的高度 + 增长的高度 =竹子开始时的高度 + 增长的高度。
等量关系:
解:设 x 时后钟状菌的高度能赶上竹子。
0.5 + 25x = 32 + 4x
21x = 31.5
x = 1.5
答:1.5时后钟状菌的高度能赶上竹子。
21x÷21 = 31.5÷21
0.5 + 25x - 0.5 - 4x = 32 + 4x - 0.5 - 4x
当堂练习
图书角有A、B两个书架,A书架上书的数量是B书架上的3倍。如果从A书架上拿出75本书放到B书架上,那么两个书架上的书就同样多了。A、B两个书架上各有多少本书?
解:设B书架上有书x本,A书架上有书3x本。
3x-x=75×2
x=75 75×3=225(本)
答:A书架上有书225本,B书架上有书75本。
课堂总结
1、列方程解决含有两个未知数的实际问题时,设其
中一个未知量为x,另一个未知量用含有x的式子
表示出来,根据题中的等量关系列方程解答。
2、解形如“ax±x= b”的方程时,先运用乘法分配
律转化为“(a±1)x=b”的形式,再根据等式的
性质求出x的值。
第1课时 邮票的张数
北师版数学五年级下册课件
七 用方程解决问题
情境导入
猜谜语
不大不大,
浑身净画,
背个纸口袋,
走遍天下。 (打一物)
谜底:邮票
邮票承载着美丽和历史,它具有观赏和收藏的价值,不少人有收集邮票的爱好。今天我们的新知识就和邮票有关,开启今天的学习吧!
探索新知
探究点 解形如“ax±x=b”的方程
你能说一说图上告诉我们哪些信息?
根据这些信息你能提出什么数学问题?
姐姐和弟弟各有多少张邮票?
探究新知
弟弟和姐姐各有多少张邮票?尝试用方程解决。
用方程求弟弟和姐姐各有多少张邮票,需要找出题中的等量关系,根据等量关系列方程解答
弟弟和姐姐的邮票张数都不知道,怎么办呢?
等量关系:
合作探究
弟弟和姐姐各有多少张邮票?尝试用方程解决。
姐姐的邮票张数=弟弟的邮票张数×3。
弟弟的邮票张数+姐姐的邮票张数=180张。
画图表示:
弟弟
姐姐
一共180张
我知道了,如果设弟弟的邮票为x张,姐姐就有3x张。
找出题中的等量关系,并画图进行表示吧!
探究新知
等量关系:
姐姐的邮票张数=弟弟的邮票张数×3。
弟弟的邮票张数+姐姐的邮票张数=180张。
x
3x
x + 3x = 180
大家还有不同的想法吗?
设弟弟有 x 张邮票
弟弟和姐姐各有多少张邮票?尝试用方程解决。
如果设姐姐的邮票为x张.....
等量关系:
姐姐的邮票张数=弟弟的邮票张数×3。
弟弟的邮票张数+姐姐的邮票张数=180张。
x
x
x + x = 180
设姐姐有 x 张邮票
还是设弟弟的邮票为x张,计算更简便。
在含有两个未知数的问题中,一般是把1倍的量设为 x,那么几倍的量就可以用几 x
表示,这样所列的方程,再求方程的解就简单一些。
x + 3x = 180
探索新知
列方程解决问题。
解:设弟弟有 x 张邮票,姐姐有 3x 张邮票。
答:弟弟有45张邮票,姐姐有135张邮票。
4x = 180
x = 45
3x = 3×45 = 135
4x ÷ 4 = 180 ÷ 4
1个x与3个x合并起来就是4个x。
探索新知
如果把“我和姐姐一共有180张邮票”改为“姐姐比我多90张邮票”,可以怎样列方程呢?
姐姐比我多90 张邮票。
等量关系:
姐姐的邮票张数=弟弟的邮票张数×3。
姐姐的邮票张数-弟弟的邮票张数=90张。
我们还是先来写等量关系式,画示意图。
画图表示:
弟弟
姐姐
90张
设弟弟有 x 张邮票,
x
3x
3x - x = 90
探索新知
弟弟和姐姐各有多少张邮票?列方程解决问题。
解:设弟弟有x张邮票,姐姐有3x张邮票。
答:弟弟有45张邮票,姐姐有135张邮票。
3x - x = 90
2x = 90
x = 45
3x = 3×45 = 135
2x ÷ 2 = 90 ÷ 2
3个x减去1个x是2个x。
探索新知
小试牛刀
源自“典中点”精选题库
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,箱子中的乒乓球没有了,羽毛球还有6个。一共取了几次?取出的乒乓球和羽毛球分别有多少个?
解:设一共取了x次。
5x-3x=6
x=3 3×5=15(个) 3×3=9(个)
答:一共取了3次,取出的乒乓球有15个,取出的羽毛球有9个。
当堂练习
源于教材P70页“练一练”
1. 根据下面题中的信息写出等量关系,再列方程解决问题。
⑴ 这幅画的长、宽各是多少厘米?
解:设宽为x cm,长为2x cm。
(x+2x)×2 = 162
3x×2÷2 = 162÷2
3x÷3 = 81÷3
x = 27
长:2x = 2×27 = 54
答:这幅画的长是54厘米,宽是27厘米。
长=宽×2
(长+宽)×2=162
等量关系:
当堂练习
源于教材P70页“练一练”
1. 根据下面题中的信息写出等量关系,再列方程解决问题。
⑵ 白键和黑键各有多少?
白键个数+黑键个数=88
白键个数-黑键个数=16
等量关系:
解:设黑键有 x 个,白键有(x+16)个。
x + 16 + x = 88
2x+ 16 -16 = 88-16
2x÷2 = 72÷2
x = 36
白键:x+16 = 36+16 = 52
答:黑键有36个,白键有52个。
当堂练习
源于教材P70页“练一练”
解:设小丽今年x岁。
3x + 4 = 37
3x - 4 = 37 - 4
3x = 33
x = 11
答:小丽今年11岁。
小丽的年龄×3 + 4 = 妈妈的年龄
等量关系:
3x÷3 = 33÷3
2. 妈妈的年龄比小丽年龄的3倍多4岁,妈妈今年37岁,小丽今年几岁?列方程解决问题。
当堂练习
源于教材P70页“练一练”
3. 平均每盘有几个橘子?
解:设平均每盘有 x 个橘子。
4x + 2 = 50
4x + 2 - 2 = 50 - 2
4x = 48
x = 12
平均每盘橘子数量×4 + 2 = 橘子总数
答:平均每盘有 12 个橘子。
等量关系:
4x÷4 = 48÷4
4.如图,正方形的周长比等边三角形的周长多 5 cm,正方形和三角形周长各是多少厘米?
当堂练习
源于教材P70页“练一练”
4x
3x
4x - 3x = 5
x = 5
正方形:4x = 4×5 = 20
三角形:3x = 3×5 = 15
解:正方形的边长是 x cm,
等边三角形的边长也是 x cm。
答:正方形周长20厘米,三角形周长15厘米。
5.
当堂练习
源于教材P70页“练一练”
如果它们都在生长旺盛期,开始时竹子高32cm,钟状菌高0.5cm。几时后钟状菌的高度能赶上竹子?先说一说等量关系,再列方程解决。
钟状菌开始时的高度 + 增长的高度 =竹子开始时的高度 + 增长的高度。
等量关系:
解:设 x 时后钟状菌的高度能赶上竹子。
0.5 + 25x = 32 + 4x
21x = 31.5
x = 1.5
答:1.5时后钟状菌的高度能赶上竹子。
21x÷21 = 31.5÷21
0.5 + 25x - 0.5 - 4x = 32 + 4x - 0.5 - 4x
当堂练习
图书角有A、B两个书架,A书架上书的数量是B书架上的3倍。如果从A书架上拿出75本书放到B书架上,那么两个书架上的书就同样多了。A、B两个书架上各有多少本书?
解:设B书架上有书x本,A书架上有书3x本。
3x-x=75×2
x=75 75×3=225(本)
答:A书架上有书225本,B书架上有书75本。
课堂总结
1、列方程解决含有两个未知数的实际问题时,设其
中一个未知量为x,另一个未知量用含有x的式子
表示出来,根据题中的等量关系列方程解答。
2、解形如“ax±x= b”的方程时,先运用乘法分配
律转化为“(a±1)x=b”的形式,再根据等式的
性质求出x的值。
