人教版八年级上册数学2024-2025学年八年级上册数学 第十一章 三角形 综合测试卷(无答案)
文档属性
| 名称 | 人教版八年级上册数学2024-2025学年八年级上册数学 第十一章 三角形 综合测试卷(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 651.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览


文档简介
第十一章综合测试卷
一、选择题
1.下列长度的3根小木棒不能搭成三角形的是 ( )
A.2cm,3cm,4cm B.1cm,2cm,3cm
C.3cm,4cm,5cm D.4cm,5cm,6cm
2.如果一个三角形两边上的高的交点在三角形的内部,那么这个三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3.满足下列条件的三角形ABC中,不是直角三角形的是 ( )
A.∠A-∠B=∠C B.∠A:∠B:∠C=3:4:7
C.∠A=2∠B=3∠C
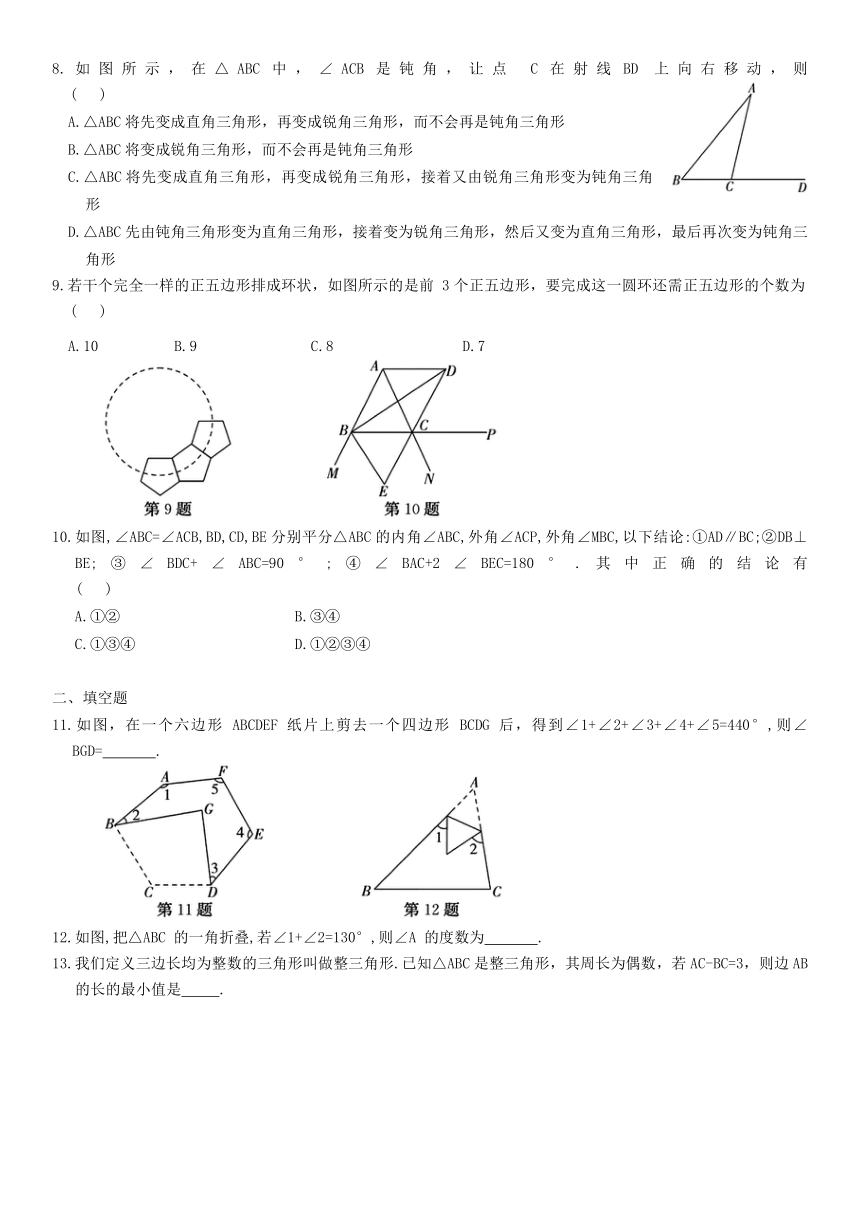
4.如图,BD是△ABC的中线,AB=5,BC=3.且△ABD的周长为11,则△BCD的周长是 ( )
A.8 B.9 C.11 D.13
5.如图,D、B、C、E四点共线, 则∠A的度数为 ( )
B.60°
6.如图,某人从点 A 出发,前进8m后向右转( ,再前进8m后又向右转( 按照这样的方式一直走下去,当他第一次回到出发点 A 时,共走了 ( )
A.24m B.32m C.40m D.48m
7.将一副常规的三角尺按如图方式放置,则图中 的度数为 ( )
8.如图所示,在△ABC中,∠ACB是钝角,让点 C在射线BD 上向右移动,则 ( )
A.△ABC将先变成直角三角形,再变成锐角三角形,而不会再是钝角三角形
B.△ABC将变成锐角三角形,而不会再是钝角三角形
C.△ABC将先变成直角三角形,再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.△ABC先由钝角三角形变为直角三角形,接着变为锐角三角形,然后又变为直角三角形,最后再次变为钝角三角形
9.若干个完全一样的正五边形排成环状,如图所示的是前 3个正五边形,要完成这一圆环还需正五边形的个数为 ( )
A.10 B.9 C.8 D.7
10.如图,∠ABC=∠ACB,BD,CD,BE分别平分△ABC的内角∠ABC,外角∠ACP,外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠BAC+2∠BEC=180°.其中正确的结论有 ( )
A.①② B.③④
C.①③④ D.①②③④
二、填空题
11.如图,在一个六边形 ABCDEF 纸片上剪去一个四边形 BCDG 后,得到∠1+∠2+∠3+∠4+∠5=440°,则∠BGD= .
12.如图,把△ABC 的一角折叠,若∠1+∠2=130°,则∠A 的度数为 .
13.我们定义三边长均为整数的三角形叫做整三角形.已知△ABC是整三角形,其周长为偶数,若AC-BC=3,则边AB的长的最小值是 .
14.如图所示,①中多边形是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的……依次类推,由正 n边形“扩展”而来的多边形的边数为 .
15.如图,BA 和CA 分别是△ABC的内角平分线和外角平分线, 是∠A BD的平分线,CA 是∠A CD的平分线,BA 是∠A BD的平分线,CA 是∠A CD的平分线,若 ,则∠A2024为
三、解答题
16.(8分)如图,△ABC为钝角三角形.
(1)作出△ABC的高AM,CN;
(2)若CN=3,AM=6,求BC与AB 的比值.
17.(9分)如图,BD是 的平分线, ,交AB于点E, 求 各内角的度数.
18.(9分)如图为一个正n边形的一部分,AB 和DC 延长后相交于点P,若 求n.
19.(9分)已知三角形的三边长分别为a,b,c,试化简|
20.(9分)如图,在 中, ,CE平分
(1)求 的度数;
(2)若 于点D, 求证: 是直角三角形.
21.(10分)已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取900°,而乙同学说,θ也能取800°,甲、乙的说法对吗 若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x的值.
22.(10分)如图,在△ABC中,A ,A ,A ,…, An为AC 边上不同的n个点,首先连接BA ,图中出现了3个不同的三角形,再连接. 图中便有6个不同的三角形……
(1)完成下表:
连接点的个数 1 2 3 4 5 6
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点
(3)若一直连接到 An,则图中共有多少个三角形
23.(11分)如图,△ABC中,∠ABC的平分线与 的外角 的平分线交于点A .
(1)当∠A 为70°时,∵∠ACD-∠ABD=∠ ,∴∠ACD-∠ABD= . ∵BA ,CA 分别是∠ABC与∠ACD 的平分线, = ;
(2)如图(2),四边形ABCD中,∠F 为∠ABC的平分线及∠DCE的平分线所在的直线构成的角,若 ,求∠F的度数;
(3)如图(3),若E为BA 延长线上一动点,连接EC,∠AEC与∠ACE的平分线交于点Q,当点 E 运动时,有下面两个结论:①∠EQC+∠A 的值为定值;( 的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.
一、选择题
1.下列长度的3根小木棒不能搭成三角形的是 ( )
A.2cm,3cm,4cm B.1cm,2cm,3cm
C.3cm,4cm,5cm D.4cm,5cm,6cm
2.如果一个三角形两边上的高的交点在三角形的内部,那么这个三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3.满足下列条件的三角形ABC中,不是直角三角形的是 ( )
A.∠A-∠B=∠C B.∠A:∠B:∠C=3:4:7
C.∠A=2∠B=3∠C
4.如图,BD是△ABC的中线,AB=5,BC=3.且△ABD的周长为11,则△BCD的周长是 ( )
A.8 B.9 C.11 D.13
5.如图,D、B、C、E四点共线, 则∠A的度数为 ( )
B.60°
6.如图,某人从点 A 出发,前进8m后向右转( ,再前进8m后又向右转( 按照这样的方式一直走下去,当他第一次回到出发点 A 时,共走了 ( )
A.24m B.32m C.40m D.48m
7.将一副常规的三角尺按如图方式放置,则图中 的度数为 ( )
8.如图所示,在△ABC中,∠ACB是钝角,让点 C在射线BD 上向右移动,则 ( )
A.△ABC将先变成直角三角形,再变成锐角三角形,而不会再是钝角三角形
B.△ABC将变成锐角三角形,而不会再是钝角三角形
C.△ABC将先变成直角三角形,再变成锐角三角形,接着又由锐角三角形变为钝角三角形
D.△ABC先由钝角三角形变为直角三角形,接着变为锐角三角形,然后又变为直角三角形,最后再次变为钝角三角形
9.若干个完全一样的正五边形排成环状,如图所示的是前 3个正五边形,要完成这一圆环还需正五边形的个数为 ( )
A.10 B.9 C.8 D.7
10.如图,∠ABC=∠ACB,BD,CD,BE分别平分△ABC的内角∠ABC,外角∠ACP,外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠BAC+2∠BEC=180°.其中正确的结论有 ( )
A.①② B.③④
C.①③④ D.①②③④
二、填空题
11.如图,在一个六边形 ABCDEF 纸片上剪去一个四边形 BCDG 后,得到∠1+∠2+∠3+∠4+∠5=440°,则∠BGD= .
12.如图,把△ABC 的一角折叠,若∠1+∠2=130°,则∠A 的度数为 .
13.我们定义三边长均为整数的三角形叫做整三角形.已知△ABC是整三角形,其周长为偶数,若AC-BC=3,则边AB的长的最小值是 .
14.如图所示,①中多边形是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的……依次类推,由正 n边形“扩展”而来的多边形的边数为 .
15.如图,BA 和CA 分别是△ABC的内角平分线和外角平分线, 是∠A BD的平分线,CA 是∠A CD的平分线,BA 是∠A BD的平分线,CA 是∠A CD的平分线,若 ,则∠A2024为
三、解答题
16.(8分)如图,△ABC为钝角三角形.
(1)作出△ABC的高AM,CN;
(2)若CN=3,AM=6,求BC与AB 的比值.
17.(9分)如图,BD是 的平分线, ,交AB于点E, 求 各内角的度数.
18.(9分)如图为一个正n边形的一部分,AB 和DC 延长后相交于点P,若 求n.
19.(9分)已知三角形的三边长分别为a,b,c,试化简|
20.(9分)如图,在 中, ,CE平分
(1)求 的度数;
(2)若 于点D, 求证: 是直角三角形.
21.(10分)已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取900°,而乙同学说,θ也能取800°,甲、乙的说法对吗 若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x的值.
22.(10分)如图,在△ABC中,A ,A ,A ,…, An为AC 边上不同的n个点,首先连接BA ,图中出现了3个不同的三角形,再连接. 图中便有6个不同的三角形……
(1)完成下表:
连接点的个数 1 2 3 4 5 6
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点
(3)若一直连接到 An,则图中共有多少个三角形
23.(11分)如图,△ABC中,∠ABC的平分线与 的外角 的平分线交于点A .
(1)当∠A 为70°时,∵∠ACD-∠ABD=∠ ,∴∠ACD-∠ABD= . ∵BA ,CA 分别是∠ABC与∠ACD 的平分线, = ;
(2)如图(2),四边形ABCD中,∠F 为∠ABC的平分线及∠DCE的平分线所在的直线构成的角,若 ,求∠F的度数;
(3)如图(3),若E为BA 延长线上一动点,连接EC,∠AEC与∠ACE的平分线交于点Q,当点 E 运动时,有下面两个结论:①∠EQC+∠A 的值为定值;( 的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值.
