北师大版数学八年级下册 第六章 平行四边形 基础复习(含答案)
文档属性
| 名称 | 北师大版数学八年级下册 第六章 平行四边形 基础复习(含答案) | 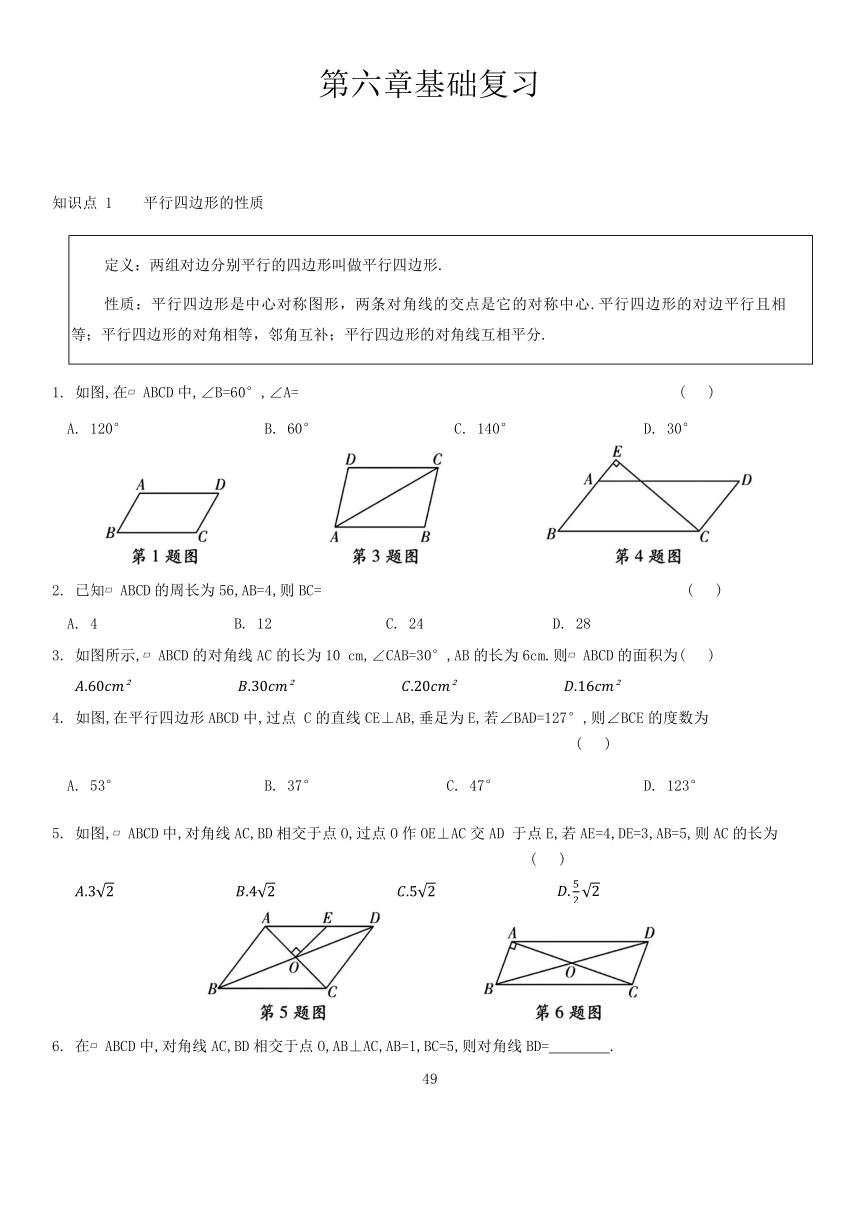 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-13 09:22:09 | ||
图片预览


文档简介
第六章基础复习
知识点 1 平行四边形的性质
定义:两组对边分别平行的四边形叫做平行四边形.
性质:平行四边形是中心对称图形,两条对角线的交点是它的对称中心.平行四边形的对边平行且相等;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
1. 如图,在 ABCD中,∠B=60°,∠A= ( )
A. 120° B. 60° C. 140° D. 30°
2. 已知 ABCD的周长为56,AB=4,则BC= ( )
A. 4 B. 12 C. 24 D. 28
3. 如图所示, ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6cm.则 ABCD的面积为( )
4. 如图,在平行四边形ABCD中,过点 C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE的度数为 ( )
A. 53° B. 37° C. 47° D. 123°
5. 如图, ABCD中,对角线AC,BD相交于点O,过点O作OE⊥AC交AD 于点E,若AE=4,DE=3,AB=5,则AC的长为 ( )
6. 在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD= .
49
7. 如图, 中,点E,F分别在BC,DE上, 求证:
8. 如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F, 连接DE.
(1)求证:AE平分∠BAD.
(2)若点 E 为BC中点,∠B=60°,AD=4,求 ABCD的面积.
知识点 2 平行四边形的判定
平行四边形的判定:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
平行线之间的距离:如果两条直线互相平行,则其中一条直线上任意一点,到另一条直线的距离都相等,这个距离称为平行线之间的距离.
9. 如图,在△ABC中,D,F分别是AB,AC上的点,且DF∥BC.点E是射线DF上一点,若再添加下列其中一个条件后,不能判定四边形DBCE 为平行四边形的是 ( )
A.∠ADE=∠E B.∠B=∠E C. DE=BC
10. 如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有 ( )
A. 4个 B. 5个 C. 8个 D. 9个
11. 学行四边形的相关知识后,小明采用下列方法钉制了一个平行四边形框架:如图,将两根木条AC,BD的中点重叠并用钉子固定,然后用木条将AB,BC,CD,DA分别钉起来.此时四边形ABCD 即为平行四边形,这样做的依据是 ( )
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
12. 如图,在四边形ABCD 中, ,对角线AC,BD 相交于点O, 26,则四边形ABCD 的面积为 .
13. 如图,在四边形ABCD中, ,点 P 自点A 向点 D 以1 cm/s的速度运动,到D点即停止.点Q自点C向B以2cm /s的速度运动,到B点即停止,点 P,Q同时出发,设运动时间为t(s).当 时,四边形APQB 是平行四边形.
14. 如图, 于点A,( 于点 D,下面结论:①AB=DC;②BE=CF;③S△ABE =S△DCF;④S ABCD =S□BCFE. 其中正确的是 .
15. 如图, ABCD中,延长AB到E,延长CD到F,使得BE=DF,试猜测AC与EF有什么关系,并加以证明.
知识点 3 三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线,三角形的中位线平行于第三边,且等于第三边的一半.
16. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是6,则△ABC的周长是
( )
A. 8 B. 10 C. 12 D. 14
17. 如图, ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为 ( )
A. 12 cm B. 9 cm C. 6 cm D. 3c m
18. 在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A 与点 D 重合,折痕为EF,则△DEF的周长为 ( )
A. 9.5 B. 10 C. 11 D. 15.5
19. 如图,在长方形ABCD中,P,R分别是BC边和DC边上的点,E,F分别是PA,PR的中点.如果 则EF的长为 .
20. 如图,等边三角形ABC中,点D,E分别为边AB,AC的中点,则 的度数为 .
21. 如图,M是 的边BC的中点,AN平分 于点N,延长BN交AC于点 D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN.
(2)求△ABC 的周长.
知识点4 多边形的内角和与外角和
n边形的内角和等于(n-2)·180°.多边形的外角和等于
22. 一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A. 10 B. 12 C. 16 D. 20
23. 如图,五边形ABCDE 的每一个内角都相等,则外角 等于 ( )
A. 62° B. 68°
24. 如图,在五边形ABCDE中,∠A+∠B+∠E=360°,DP,CP分别平分. ,则∠P 的度数是 ( )
A. 70° B. 65° C. 60° D. 55°
25. 将正三角形、正方形、正五边形按如图所示的位置摆放,且每一个图形的一个顶点都在另一个图形的一条边上,则∠1+∠2+∠3= 度.
26. 从如图的五边形ABCDE纸片周围减去一个三角形,剩余部分的多边形的内角和是 .
知识点 1 平行四边形的性质
定义:两组对边分别平行的四边形叫做平行四边形.
性质:平行四边形是中心对称图形,两条对角线的交点是它的对称中心.平行四边形的对边平行且相等;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
1. 如图,在 ABCD中,∠B=60°,∠A= ( )
A. 120° B. 60° C. 140° D. 30°
2. 已知 ABCD的周长为56,AB=4,则BC= ( )
A. 4 B. 12 C. 24 D. 28
3. 如图所示, ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6cm.则 ABCD的面积为( )
4. 如图,在平行四边形ABCD中,过点 C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE的度数为 ( )
A. 53° B. 37° C. 47° D. 123°
5. 如图, ABCD中,对角线AC,BD相交于点O,过点O作OE⊥AC交AD 于点E,若AE=4,DE=3,AB=5,则AC的长为 ( )
6. 在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD= .
49
7. 如图, 中,点E,F分别在BC,DE上, 求证:
8. 如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F, 连接DE.
(1)求证:AE平分∠BAD.
(2)若点 E 为BC中点,∠B=60°,AD=4,求 ABCD的面积.
知识点 2 平行四边形的判定
平行四边形的判定:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
平行线之间的距离:如果两条直线互相平行,则其中一条直线上任意一点,到另一条直线的距离都相等,这个距离称为平行线之间的距离.
9. 如图,在△ABC中,D,F分别是AB,AC上的点,且DF∥BC.点E是射线DF上一点,若再添加下列其中一个条件后,不能判定四边形DBCE 为平行四边形的是 ( )
A.∠ADE=∠E B.∠B=∠E C. DE=BC
10. 如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有 ( )
A. 4个 B. 5个 C. 8个 D. 9个
11. 学行四边形的相关知识后,小明采用下列方法钉制了一个平行四边形框架:如图,将两根木条AC,BD的中点重叠并用钉子固定,然后用木条将AB,BC,CD,DA分别钉起来.此时四边形ABCD 即为平行四边形,这样做的依据是 ( )
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
12. 如图,在四边形ABCD 中, ,对角线AC,BD 相交于点O, 26,则四边形ABCD 的面积为 .
13. 如图,在四边形ABCD中, ,点 P 自点A 向点 D 以1 cm/s的速度运动,到D点即停止.点Q自点C向B以2cm /s的速度运动,到B点即停止,点 P,Q同时出发,设运动时间为t(s).当 时,四边形APQB 是平行四边形.
14. 如图, 于点A,( 于点 D,下面结论:①AB=DC;②BE=CF;③S△ABE =S△DCF;④S ABCD =S□BCFE. 其中正确的是 .
15. 如图, ABCD中,延长AB到E,延长CD到F,使得BE=DF,试猜测AC与EF有什么关系,并加以证明.
知识点 3 三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线,三角形的中位线平行于第三边,且等于第三边的一半.
16. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是6,则△ABC的周长是
( )
A. 8 B. 10 C. 12 D. 14
17. 如图, ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为 ( )
A. 12 cm B. 9 cm C. 6 cm D. 3c m
18. 在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A 与点 D 重合,折痕为EF,则△DEF的周长为 ( )
A. 9.5 B. 10 C. 11 D. 15.5
19. 如图,在长方形ABCD中,P,R分别是BC边和DC边上的点,E,F分别是PA,PR的中点.如果 则EF的长为 .
20. 如图,等边三角形ABC中,点D,E分别为边AB,AC的中点,则 的度数为 .
21. 如图,M是 的边BC的中点,AN平分 于点N,延长BN交AC于点 D,已知AB=10,BC=15,MN=3.
(1)求证:BN=DN.
(2)求△ABC 的周长.
知识点4 多边形的内角和与外角和
n边形的内角和等于(n-2)·180°.多边形的外角和等于
22. 一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A. 10 B. 12 C. 16 D. 20
23. 如图,五边形ABCDE 的每一个内角都相等,则外角 等于 ( )
A. 62° B. 68°
24. 如图,在五边形ABCDE中,∠A+∠B+∠E=360°,DP,CP分别平分. ,则∠P 的度数是 ( )
A. 70° B. 65° C. 60° D. 55°
25. 将正三角形、正方形、正五边形按如图所示的位置摆放,且每一个图形的一个顶点都在另一个图形的一条边上,则∠1+∠2+∠3= 度.
26. 从如图的五边形ABCDE纸片周围减去一个三角形,剩余部分的多边形的内角和是 .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
