人教版2024-2025学年八年级上册数学第13.3章-第13.4章基础测试卷(含答案)
文档属性
| 名称 | 人教版2024-2025学年八年级上册数学第13.3章-第13.4章基础测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1017.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览



文档简介
第13.3章-第13.4章基础测试卷
一、选择题
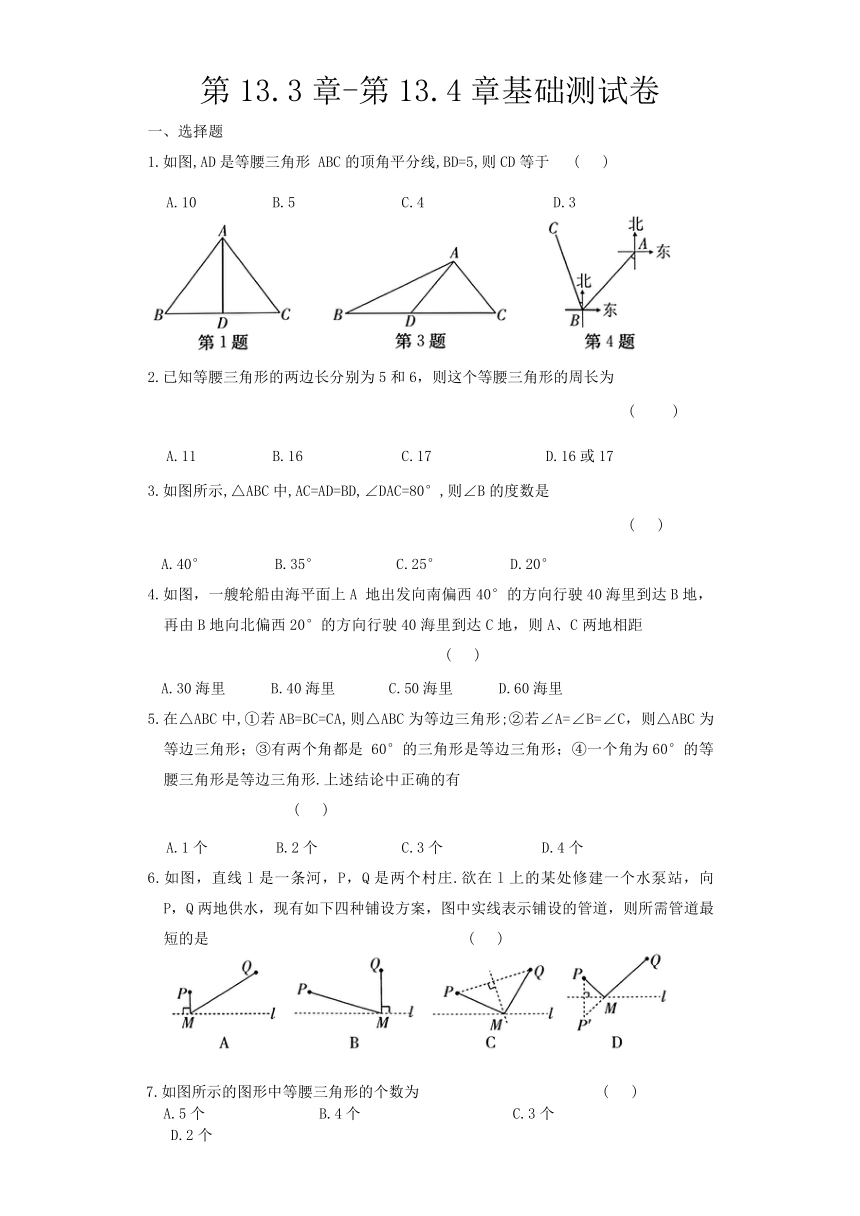
1.如图,AD是等腰三角形 ABC的顶角平分线,BD=5,则CD等于 ( )
A.10 B.5 C.4 D.3
2.已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为
( )
A.11 B.16 C.17 D.16或17
3.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是
( )
A.40° B.35° C.25° D.20°
4.如图,一艘轮船由海平面上A 地出发向南偏西40°的方向行驶40海里到达B地,再由B地向北偏西20°的方向行驶40海里到达C地,则A、C两地相距 ( )
A.30海里 B.40海里 C.50海里 D.60海里
5.在△ABC中,①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是 60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图,直线l是一条河,P,Q是两个村庄.欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是 ( )
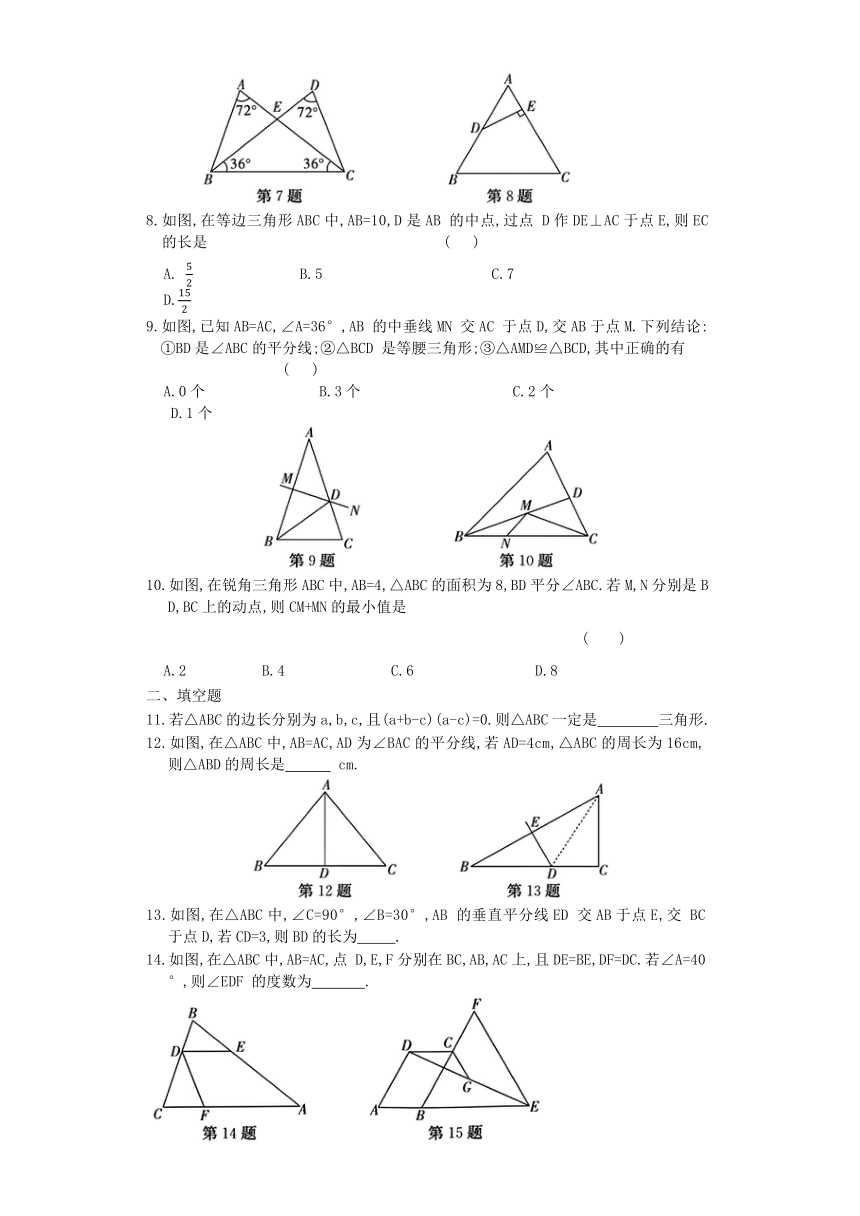
7.如图所示的图形中等腰三角形的个数为 ( )
A.5个 B.4个 C.3个 D.2个
8.如图,在等边三角形ABC中,AB=10,D是AB 的中点,过点 D作DE⊥AC于点E,则EC的长是 ( )
A. B.5 C.7 D.
9.如图,已知AB=AC,∠A=36°,AB 的中垂线MN 交AC 于点D,交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD 是等腰三角形;③△AMD≌△BCD,其中正确的有 ( )
A.0个 B.3个 C.2个 D.1个
10.如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M,N分别是BD,BC上的动点,则CM+MN的最小值是
( )
A.2 B.4 C.6 D.8
二、填空题
11.若△ABC的边长分别为a,b,c,且(a+b-c)(a-c)=0.则△ABC一定是 三角形.
12.如图,在△ABC中,AB=AC,AD为∠BAC的平分线,若AD=4cm,△ABC的周长为16cm,则△ABD的周长是 cm.
13.如图,在△ABC中,∠C=90°,∠B=30°,AB 的垂直平分线ED 交AB于点E,交 BC于点D,若CD=3,则BD的长为 .
14.如图,在△ABC中,AB=AC,点 D,E,F分别在BC,AB,AC上,且DE=BE,DF=DC.若∠A=40°,则∠EDF 的度数为 .
15.如图, 的顶点C在等边三角形BEF 的边BF 上,点 E在AB的延长线上,G为DE 的中点,连接CG.若 ,则CG的长为 .
三、解答题
16.(7分)如图,在 中, ,AD是BC 边上的中线, 于点E.求证:
17.(8分)等腰三角形的一个角是 ,求它的另外两个角的度数.
18.(8分)如图, 是一个直角三角形,其中 ,垂足分别是 那么. 的长是多少
19.(8分)如图,在 中,点 D,E分别是AB,AC边上的点, CE, ,BE与CD 相交于点F.求证: 是等腰三角形.
20.(8 分)如图,在. 中, ,垂足为点 E, 是等边三角形.若 ,求BE的长.
21.(10分)如图,在 中, ,O为AB 的中点,D,E分别在AC,BC上,且 求证:(
22.(10分)(1)如图1,在△ABC中,∠ABC,∠ACB的平分线交于点O,过点 O作EF∥BC分别交AB,AC于点E,F,试猜想EF,BE,CF之间有怎样的数量关系,并说明理由;
(2)如图2,将图1中∠ACB的平分线改为外角∠ACD 的平分线,其他条件不变,则(1)中的结论还成立吗 请说明理由.
23.(11分)如图,已知 AB与CD 相交于O,ON 平分∠AOD,若AB=CD,∠AOC=60°,连接NA,NC,且NA=NC.
(1)求证:∠A=∠C;
(2)连接NB,ND,BD,判断△NBD的形状,并说明理由.
第13.3章-第13.4章基础测试卷
B 2、D 3、C 4、B 5、D 6、D 7、A 8、D 9、C 10、B
11、等腰 12、12 13、6 14、70° 15、
16、证明:∵AB=AC,AD是BC边上的中线,
∴∠CAD=∠BAD,AD⊥BC.
∵BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°.
∴∠CBE=∠CAD.∴∠CBE=∠BAD.
解:分两种情况:①当50°角为顶角时,另两个角为底角,度数为 ;
②当50°角为底角时,另两个角分别为底角和顶角,底角度数为50°,顶角度数为 所以另两个角的度数是65°,65°或50°,80°.
解:在 Rt△ABC中,
,
又 ∵ ∠A + ∠B = 90°,
∴ 在 中,
=7.5( cm).
∵在 中, =3.75( cm).
证明:在 与 中 △BDF≌△CEF(AAS),
∴BF=CF,∴∠FBC=
即∠ABC=∠ACB,
∴AB=AC,∴△ABC是等腰三角形.
解:∵△BDE 是等边三角形,
∴∠DBE=60°.
∵在△ABC中,∠C=∠ABC,BE⊥AC,
∴∠C=∠ABC=∠ABE+∠EBC,则∠EBC=∠ABC-60°=∠C--60°,∠BEC=90°,
∴∠EBC+∠C=90°,即∠C--60°+∠C=90°,则∠C=75°,
∴∠ABC=75°,∴∠A=30°.
∵∠AED=90°-∠DEB=30°,∴∠A=∠AED,∴DE=AD=4,∴BE=DE=4.
.证明:如图,连接OC.∵AC=BC,O为AB 的中点,
=90°,∴∠A=∠B=∠ACO=∠BCO=45°,
∴OC
∠COE=90°.
∵∠AOD+∠DOC=90°.∴∠AOD=∠COE.
∵∠A=∠ECO,OA=OC,∴△OAD≌△OCE(ASA),∴AD=CE.
∵AC=AD+CD,∴CE+CD=AC.
解:(1)EF=BE+CF.理由如下:∵BO平分∠ABC,CO 平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB.
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,即EF=BE+CF.
(2)不成立.理由如下:∵BO平分∠ABC,CO 平分∠ACD,
∴∠EBO=∠OBC,∠FCO=∠OCD.
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCD,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE-OF=BE-CF,即EF=BE-CF.
23、(1)证明:如图,过 N 作 NE⊥AB 于E,NF⊥CD 于 F,
∴∠AEN=∠CFN=90°,∵ON 平分∠AOD,
∴NE=NF,在 Rt△AEN
与 Rt△CFN 中,
△AEN≌Rt△CFN(HL),
∴∠A=∠C. (2)解: 是等边三角
形.理由:在△ANB 和△CND 中,
(SAS),
∴BN=DN,∠ABN=∠CDN,设BN与CD 交于G,
∵∠DGN=∠BGO.∴∠DNG=∠BOG,
∵∠AOC=∠BOD=60°,∴∠DNB=60°,∴△NBD 是等边三角形.
一、选择题
1.如图,AD是等腰三角形 ABC的顶角平分线,BD=5,则CD等于 ( )
A.10 B.5 C.4 D.3
2.已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为
( )
A.11 B.16 C.17 D.16或17
3.如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是
( )
A.40° B.35° C.25° D.20°
4.如图,一艘轮船由海平面上A 地出发向南偏西40°的方向行驶40海里到达B地,再由B地向北偏西20°的方向行驶40海里到达C地,则A、C两地相距 ( )
A.30海里 B.40海里 C.50海里 D.60海里
5.在△ABC中,①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是 60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图,直线l是一条河,P,Q是两个村庄.欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是 ( )
7.如图所示的图形中等腰三角形的个数为 ( )
A.5个 B.4个 C.3个 D.2个
8.如图,在等边三角形ABC中,AB=10,D是AB 的中点,过点 D作DE⊥AC于点E,则EC的长是 ( )
A. B.5 C.7 D.
9.如图,已知AB=AC,∠A=36°,AB 的中垂线MN 交AC 于点D,交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD 是等腰三角形;③△AMD≌△BCD,其中正确的有 ( )
A.0个 B.3个 C.2个 D.1个
10.如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M,N分别是BD,BC上的动点,则CM+MN的最小值是
( )
A.2 B.4 C.6 D.8
二、填空题
11.若△ABC的边长分别为a,b,c,且(a+b-c)(a-c)=0.则△ABC一定是 三角形.
12.如图,在△ABC中,AB=AC,AD为∠BAC的平分线,若AD=4cm,△ABC的周长为16cm,则△ABD的周长是 cm.
13.如图,在△ABC中,∠C=90°,∠B=30°,AB 的垂直平分线ED 交AB于点E,交 BC于点D,若CD=3,则BD的长为 .
14.如图,在△ABC中,AB=AC,点 D,E,F分别在BC,AB,AC上,且DE=BE,DF=DC.若∠A=40°,则∠EDF 的度数为 .
15.如图, 的顶点C在等边三角形BEF 的边BF 上,点 E在AB的延长线上,G为DE 的中点,连接CG.若 ,则CG的长为 .
三、解答题
16.(7分)如图,在 中, ,AD是BC 边上的中线, 于点E.求证:
17.(8分)等腰三角形的一个角是 ,求它的另外两个角的度数.
18.(8分)如图, 是一个直角三角形,其中 ,垂足分别是 那么. 的长是多少
19.(8分)如图,在 中,点 D,E分别是AB,AC边上的点, CE, ,BE与CD 相交于点F.求证: 是等腰三角形.
20.(8 分)如图,在. 中, ,垂足为点 E, 是等边三角形.若 ,求BE的长.
21.(10分)如图,在 中, ,O为AB 的中点,D,E分别在AC,BC上,且 求证:(
22.(10分)(1)如图1,在△ABC中,∠ABC,∠ACB的平分线交于点O,过点 O作EF∥BC分别交AB,AC于点E,F,试猜想EF,BE,CF之间有怎样的数量关系,并说明理由;
(2)如图2,将图1中∠ACB的平分线改为外角∠ACD 的平分线,其他条件不变,则(1)中的结论还成立吗 请说明理由.
23.(11分)如图,已知 AB与CD 相交于O,ON 平分∠AOD,若AB=CD,∠AOC=60°,连接NA,NC,且NA=NC.
(1)求证:∠A=∠C;
(2)连接NB,ND,BD,判断△NBD的形状,并说明理由.
第13.3章-第13.4章基础测试卷
B 2、D 3、C 4、B 5、D 6、D 7、A 8、D 9、C 10、B
11、等腰 12、12 13、6 14、70° 15、
16、证明:∵AB=AC,AD是BC边上的中线,
∴∠CAD=∠BAD,AD⊥BC.
∵BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°.
∴∠CBE=∠CAD.∴∠CBE=∠BAD.
解:分两种情况:①当50°角为顶角时,另两个角为底角,度数为 ;
②当50°角为底角时,另两个角分别为底角和顶角,底角度数为50°,顶角度数为 所以另两个角的度数是65°,65°或50°,80°.
解:在 Rt△ABC中,
,
又 ∵ ∠A + ∠B = 90°,
∴ 在 中,
=7.5( cm).
∵在 中, =3.75( cm).
证明:在 与 中 △BDF≌△CEF(AAS),
∴BF=CF,∴∠FBC=
即∠ABC=∠ACB,
∴AB=AC,∴△ABC是等腰三角形.
解:∵△BDE 是等边三角形,
∴∠DBE=60°.
∵在△ABC中,∠C=∠ABC,BE⊥AC,
∴∠C=∠ABC=∠ABE+∠EBC,则∠EBC=∠ABC-60°=∠C--60°,∠BEC=90°,
∴∠EBC+∠C=90°,即∠C--60°+∠C=90°,则∠C=75°,
∴∠ABC=75°,∴∠A=30°.
∵∠AED=90°-∠DEB=30°,∴∠A=∠AED,∴DE=AD=4,∴BE=DE=4.
.证明:如图,连接OC.∵AC=BC,O为AB 的中点,
=90°,∴∠A=∠B=∠ACO=∠BCO=45°,
∴OC
∠COE=90°.
∵∠AOD+∠DOC=90°.∴∠AOD=∠COE.
∵∠A=∠ECO,OA=OC,∴△OAD≌△OCE(ASA),∴AD=CE.
∵AC=AD+CD,∴CE+CD=AC.
解:(1)EF=BE+CF.理由如下:∵BO平分∠ABC,CO 平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB.
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,即EF=BE+CF.
(2)不成立.理由如下:∵BO平分∠ABC,CO 平分∠ACD,
∴∠EBO=∠OBC,∠FCO=∠OCD.
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCD,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE-OF=BE-CF,即EF=BE-CF.
23、(1)证明:如图,过 N 作 NE⊥AB 于E,NF⊥CD 于 F,
∴∠AEN=∠CFN=90°,∵ON 平分∠AOD,
∴NE=NF,在 Rt△AEN
与 Rt△CFN 中,
△AEN≌Rt△CFN(HL),
∴∠A=∠C. (2)解: 是等边三角
形.理由:在△ANB 和△CND 中,
(SAS),
∴BN=DN,∠ABN=∠CDN,设BN与CD 交于G,
∵∠DGN=∠BGO.∴∠DNG=∠BOG,
∵∠AOC=∠BOD=60°,∴∠DNB=60°,∴△NBD 是等边三角形.
