第1-3单元期中应用题易错大集结(含解析)-数学六年级上册苏教版
文档属性
| 名称 | 第1-3单元期中应用题易错大集结(含解析)-数学六年级上册苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 463.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-3单元期中应用题易错大集结-数学六年级上册苏教版
一、解答题
1.一个长方体水池,从里面量,长是24米,宽是8米,深是2米.如果在这个水池里蓄水288立方米,水深多少米?如果在水池的底面和四周抹上水泥,抹水泥的面积是多少平方米?
2.一个长方体的玻璃缸,长8分米,宽7分米,高6分米,水深5.5分米。如果投入一块棱长为4分米的正方形铁块,缸里的水溢出多少升?
3.一个封闭的长方体玻璃容器(玻璃厚度忽略不计)长20厘米,宽10厘米,高40厘米,容器中水深25厘米.如果把这个容器以前面为底面平放在桌上,这时水面离容器口多少厘米?
4.光明度假村要建一个长方体游泳池。长50米,宽35米,深2米。
(1)这个游泳池占地多少平方米?
(2)在游泳池底面和四壁抹水泥,抹水泥的面积是多少平方米?
(3)游泳池水深1.6米,水的体积是多少立方米?
5.一个长方体水箱,从里面量长是8dm,宽6dm,高5dm,水箱里装着水,水面距水箱的上沿1.5dm。水箱内的水有多少升?
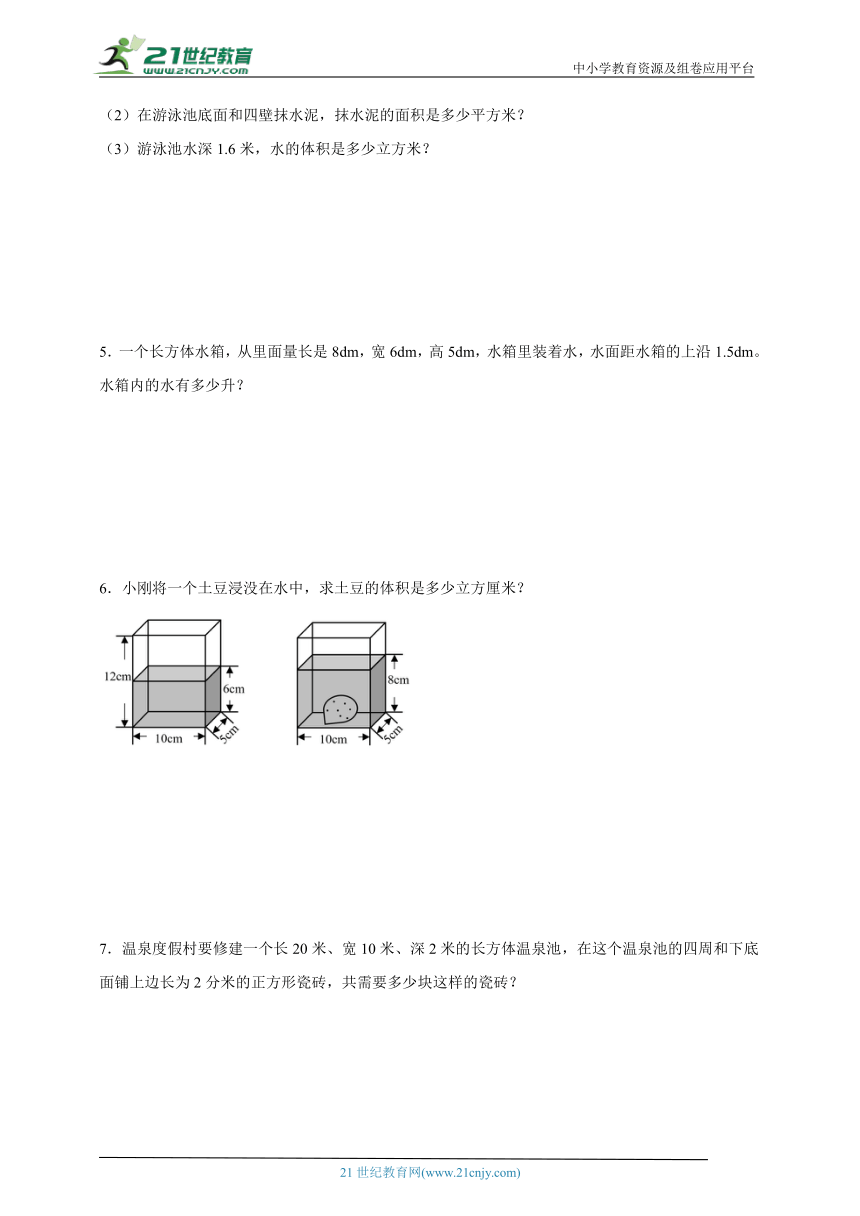
6.小刚将一个土豆浸没在水中,求土豆的体积是多少立方厘米?
7.温泉度假村要修建一个长20米、宽10米、深2米的长方体温泉池,在这个温泉池的四周和下底面铺上边长为2分米的正方形瓷砖,共需要多少块这样的瓷砖?
8.一节长方体的通风管长是3分米,宽是2分米,高是8分米。做一节这样的通风管至少需要多大的铁皮?
9.把一个棱长4分米的正方体的一个角挖掉一个棱长1分米的小正方体,如图,所得立体图形的表面积是多少?
10.李师傅每小时织米长的毯子,小时织多少米?
11.食堂有煤吨,用去一部分后还剩。还剩多少吨?
12.一个捕鱼队九月份捕鱼63吨,十月份比九月份多捕。十月份捕鱼多少吨?
13.菜场运来白菜750千克,运来的萝卜比白菜少,运来萝卜多少千克?
14.本场数学考试的时间为90分钟,当你做到这一题时,时间大约过去了,如果剩下的题目解答还需要的时间,那么做完整张试卷后检查的时间约占总时间的几分之几?约为多少分钟?
15.赵老师家到学校的路程是千米,他先骑车行了全程的到达商店,此时距离学校还有多远?(请先在图中用“△”标出商店的大致位置,再解答题目)
16.深圳,简称“深”,别称“鹏城”,中国四大一线城市之一,是国际科技产业创新中心。全市面积大约2000平方千米,其中宝安区面积最大,约占全市面积的,盐田区面积最小,约占全市面积的。宝安区和盐田区的面积大约各是多少平方千米?
17.爸爸今年36岁,我今年的年龄是爸爸年龄的,是爷爷年龄的。爷爷今年多少岁?
18.信辉小区有三个快递网点:申通快递、顺丰快递、韵达快递,申通快递网点的人数是顺丰快递的,韵达快递网点人数是顺丰快递的,申通快递网点有20人,韵达快递网点有多少人?
19.下图的总面积是156平方厘米,两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,大、小长方形面积的比是多少?大长方形面积是多少?
20.六(1)班、六(2)班学生数的比是7∶8,如果从六(2)班调8人到六(1)班,则六(1)班、六(2)班学生数的比是5∶4,两班共有多少人?
21.学校合唱社团和舞蹈社团共有56人,舞蹈社团的人数是合唱社团的。合唱社团和舞蹈社团各有多少人?
22.有一个长方体木箱,底面是一个正方形,它的前面和底面的面积比是5∶2。制作这个木箱用了360平方分米的木板,这个长方体木箱的底面积是多少平方分米?(木板的厚度和接头处忽略不计)
23.航模比赛,学校买来184架飞机模型,按1∶3∶4的比例分给四、五、六年级,每个年级各分得多少架飞机模型?
24.甲、乙两地相距240千米,A、B两辆汽车同时从甲、乙两地相对开出,1.5小时相遇,A、B两辆汽车的速度比是3∶5,A、B两辆汽车平均每小时分别行多少千米?
参考答案:
1.水深:1.5米;抹水泥面积320平方米
【详解】288÷(24×8)=1.5(米)
(24×2+8×2)×2+24×8=320(平方米)
2.36升
【分析】根据题意可知,把铁块放入玻璃缸中,溢出水的体积等于铁块的体积减去玻璃缸内无水部分的体积,根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,把数据代入公式解答。
【详解】4×4×4-8×7×(6-5.5)
=64-56×0.5
=64-28
=36(立方分米)
36立方分米=36升
答:缸里的水溢出36升。
【点睛】此题主要考查正方体的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
3.3.75厘米
【详解】10-20×10×25÷(40×20)=3.75(厘米)
4.(1)1750平方米;(2)2090平方米;(3)2800立方米。
【分析】(1)求这个游泳池的占地面积,只与游泳池的底面面积有关,利用长方形的面积公式:长×宽即可解决。
(2)在游泳池底面和四壁抹水泥即没有上面,只有5个面,根据公式:长×宽+(长×高+宽×高)×2即可求解。
(3)根据长方体的体积公式:长×宽×高即可求解。
【详解】(1)50×35=1750(平方米)
答:这个游泳池占地1750平方米。
(2)50×35+(50×2+35×2)×2
=1750+(100+70)×2
=1750+170×2
=1750+340
=2090(平方米)
答:抹水泥的面积是2090平方米。
(3)50×35×1.6
=1750×1.6
=2800(立方米)
答:水的体积是2800立方米。
【点睛】本题考查长方体的表面积和体积公式,要重点掌握。
5.168升
【分析】求容积的方法和求体积的方法一样,,结果注意单位换算,据此解答。
【详解】
=8×6×(5-1.5)
=48×3.5
=168(立方分米)
168立方分米=168升
答:水箱内的水有168升。
【点睛】本题考查长方体的容积,注意长方体容积的计算方法和体积计算方法一样,结果要换算单位。
6.100立方厘米
【分析】此题考查用“排水法”去求不规则物体的体积。将一个重物放入一个规则的装有水的容器中完全淹没,水面上升,物体排开水的体积,就是物体的体积,这种方法就是排水法。在此题中,土豆的体积就是水上升的体积,就是一个长为10厘米,宽5厘米,高2厘米的长方体体积,根据长方体体积计算公式计算得出答案。
【详解】(cm)
(立方厘米)
答:土豆的体积是100立方厘米。
7.8000块
【分析】先求出铺瓷砖的面积,再用铺瓷砖的面积÷瓷砖面积即可。温泉池没有上面,铺瓷砖的面积=长×宽+长×高×2+宽×高×2,据此列式解答,注意统一单位。
【详解】20×10+20×2×2+10×2×2
=200+80+40
=320(平方米)
2分米=0.2米
320÷(0.2×0.2)
=320÷0.04
=8000(块)
答:共需要8000块这样的瓷砖。
8.44平方分米
【分析】首先搞清这道题是求长方体的侧面积,其次这个长方体的侧面由四个长方形组成,缺少最大的两个面用铁皮最少,也就是缺少前后两个面;只求它的左右、上下4个面的面积之和;据此解答即可。
【详解】3×2×2+2×8×2
=12+32
=44(平方分米)
答:做一节这样的通风管至少需要44平方分米的铁皮。
【点睛】如能画示长方体意图会使题意更加清楚明了,有助于进一步分析和解答。
9.96平方分米
【分析】这个正方体从一个角挖掉一个棱长1分米的正方体,等于这个正方体去掉了3个边长1分米的正方形的面积,又新增加了3个棱长1分米的正方形的面积,与原正方体的表面积相等,由此即可根据正方体的表面积公式:棱长×棱长×6,把数代入即可求解。
【详解】由分析可知,这个立体图形的表面积:
4×4×6
=16×6
=96(平方分米)
答:这个立体图形的表面积是96平方分米。
【点睛】此题主要是考查正方体的表面积,关键明白从这个正方体从一个角挖掉一个棱长1分米的正方体,与原正方体表面积不变。
10.米
【分析】每小时织的长度×相应时间=相应时间织的长度。
【详解】(米)
答:小时织米。
11.吨
【分析】还剩,就是将食堂煤的重量看成单位“1”,则剩下占总质量的,求一个数的几分之几用乘法。
【详解】(吨)
答:还剩吨。
12.81吨
【分析】把九月份捕鱼的吨数看作单位“1”,已知十月份比九月份多捕,那么九月份捕鱼吨数的(1+)就是十月份捕鱼的吨数,用九月份捕鱼的吨数乘(1+)即可求出十月份捕鱼的吨数。
【详解】63×(1+)
=63×
=81(吨)
答:十月份捕鱼81吨。
13.300千克
【分析】把白菜的质量看作单位“1”,已知运来的萝卜比白菜少,那么运来的萝卜就是白菜的(1-),用白菜的质量乘(1-)即可解答。
【详解】750×(1-)
=750×
=300(千克)
答:运来的萝卜有300千克。
14.;13.5分钟
【分析】把总时间看作单位“1”,根据分数减法的意义,用1--即可求出做完整张试卷后检查的时间约占总时间的几分之几;根据分数乘法的意义,用总时间乘(1--)即可求出做完整张试卷后检查的时间。
【详解】1--=
90×=13.5(分钟)
答:做完整张试卷后检查的时间约占总时间的;约为13.5分钟。
15.千米;图见详解
【分析】根据求一个数的几分之几是多少,用乘法计算,用乘法计算出商店的位置,再用全长减去赵老师骑到商店的路程,即可求出剩下的路程;再从赵老师家往学校方向大约在全长的用标出“△”即可。
【详解】×=(千米)
-=(千米)
作图如下:
答:此时距离学校还有千米。
16.400平方千米;75平方千米
【分析】从“占全市面积的,全市面积的”可知,以全市面积为单位“1”,根据求一个数的几分之几,用乘法计算。分别用全市面积×对应分率,即可求出宝安区和盐田区的面积。据此解答。
【详解】宝安区:2000×=400(平方千米)
盐田区:2000×=75(平方千米)
答:宝安区的面积大约是400平方千米,盐田区的面积大约各是75平方千米。
17.72岁
【分析】把爸爸今年的年龄看作单位“1”, 我今年的年龄是爸爸年龄的,用爸爸今年的年龄×,求出我今年的年龄,再把爷爷今年的年龄看作单位“1”,爷爷年龄的,对应的是我今年的年龄,求爷爷今年的年龄,用我今年的年龄÷,即可解答。
【详解】36×÷
=6÷
=6×12
=72(岁)
答:爷爷今年72岁。
18.12人
【分析】已知申通快递网点有20人,是顺丰快递的,把顺丰快递的人数看作单位“1”,单位“1”未知,用申通快递网点的人数除以,求出顺丰快递的人数;
已知韵达快递网点人数是顺丰快递的,把顺丰快递的人数看作单位“1”,单位“1”已知,用顺丰快递的人数乘,求出韵达快递网点的人数。
【详解】20÷×
=20××
=30×
=12(人)
答:韵达快递网点有12人。
19.4∶3;96平方厘米
【分析】(1)设重叠部分的面积是1,先把大长方形的面积看成单位“1”,它的对应数量是重叠部分的面积,由此用除法求出大长方形的面积;同理把小长方形的面积看成单位“1”,它的对应数量是重叠部分的面积,由此用除法求出小长方形的面积;然后用大长方形的面积比上小长方形的面积即可。
(2)由题意可知,重叠部分的面积是1份,则大长方形的面积是8份,小长方形的面积是6份,大长方形的面积加上小长方形的面积减去重叠部分的面积是8+6-1=13(份),这13份就是图形的总面积,用总面积除以总份数,求出1份是多少,再乘大长方形的份数即可解答。
【详解】1÷=8
1÷=6
8∶6
=(8÷2)∶(6÷2)
=4∶3
156÷(8+6-1)
=156÷13
=12(平方厘米)
12×8=96(平方厘米)
答:大、小长方形面积的比是4∶3,大长方形的面积是96平方厘米。
20.90人
【分析】将两班总人数看作单位“1”,根据六(1)班、六(2)班学生数的比是7∶8,可知原来六(1)班是六(2)班学生数的;从六(2)班调8人到六(1)班,六(1)班是六(2)班学生数的,说明8人的对应分率是(-),根据部分数量÷对应分率=整体数量,即可求出两班总人数。
【详解】8÷(-)
=8÷(-)
=8÷
=8×
=90(人)
答:两班共有90人。
21.32人;24人
【分析】从“舞蹈社团的人数是合唱社团的”可知,舞蹈社团的人数∶合唱社团的人数=3∶4。以合唱社团和舞蹈社团总人数为单位“1”,合唱社团的人数占总人数的。根据求一个数的几分之几是多少,用乘法计算,用总人数×即可求出合唱社团的人数,再用总人数-合唱社团的人数,即可求出舞蹈社团的人数。据此解答。
【详解】=3∶4
合唱社团的人数:
56×
=56×
=32(人)
舞蹈社团:56-32=24(人)
答:合唱社团有32人,舞蹈社团有24人。
22.30平方分米
【分析】
长方体一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。如图,这个长方体木箱前后左右4个面完全一样,上下面是完全一样的正方形,它的前面和底面的面积比是5∶2,因此前后左右4个面和上下两个面的比是(5×4)∶(2×2),表面积÷总份数,求出一份数,一份数×底面对应份数=底面积,据此列式解答。
【详解】360÷(5×4+2×2)×2
=360÷(20+4)×2
=360÷24×2
=15×2
=30(平方分米)
答:这个长方体木箱的底面积是30平方分米。
23.四年级分得23架飞机模型,五年级分得69架飞机模型,六年级分得92架飞机模型。
【分析】已知模型飞机的总数,和分配比例,用总数量除以总份数,和所占份数就等于一个年级分得飞机模型的数量,据此解答。
【详解】总份数:1+3+4=8
四年级:184÷8×1=23(架)
五年级:184÷8×3
=23×3
=69(架)
六年级:184÷8×4
=23×4
=92(架)
答:四、五、六年级,每个年级各分得23架、69架、92架飞机模型。
24.60千米;100千米
【分析】根据速度和=总路程÷相遇时间,求出两车速度和,将比的前后项看成份数,速度和÷总份数,求出一份数,一份数分别乘A、B两车对应分率,即可求出A、B两车速度。
【详解】240÷1.5÷(3+5)
=160÷8
=20(千米)
20×3=60(千米/小时)
20×5=100(千米/小时)
答:A辆汽车平均每小时行60千米,B辆汽车平均每小时行100千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-3单元期中应用题易错大集结-数学六年级上册苏教版
一、解答题
1.一个长方体水池,从里面量,长是24米,宽是8米,深是2米.如果在这个水池里蓄水288立方米,水深多少米?如果在水池的底面和四周抹上水泥,抹水泥的面积是多少平方米?
2.一个长方体的玻璃缸,长8分米,宽7分米,高6分米,水深5.5分米。如果投入一块棱长为4分米的正方形铁块,缸里的水溢出多少升?
3.一个封闭的长方体玻璃容器(玻璃厚度忽略不计)长20厘米,宽10厘米,高40厘米,容器中水深25厘米.如果把这个容器以前面为底面平放在桌上,这时水面离容器口多少厘米?
4.光明度假村要建一个长方体游泳池。长50米,宽35米,深2米。
(1)这个游泳池占地多少平方米?
(2)在游泳池底面和四壁抹水泥,抹水泥的面积是多少平方米?
(3)游泳池水深1.6米,水的体积是多少立方米?
5.一个长方体水箱,从里面量长是8dm,宽6dm,高5dm,水箱里装着水,水面距水箱的上沿1.5dm。水箱内的水有多少升?
6.小刚将一个土豆浸没在水中,求土豆的体积是多少立方厘米?
7.温泉度假村要修建一个长20米、宽10米、深2米的长方体温泉池,在这个温泉池的四周和下底面铺上边长为2分米的正方形瓷砖,共需要多少块这样的瓷砖?
8.一节长方体的通风管长是3分米,宽是2分米,高是8分米。做一节这样的通风管至少需要多大的铁皮?
9.把一个棱长4分米的正方体的一个角挖掉一个棱长1分米的小正方体,如图,所得立体图形的表面积是多少?
10.李师傅每小时织米长的毯子,小时织多少米?
11.食堂有煤吨,用去一部分后还剩。还剩多少吨?
12.一个捕鱼队九月份捕鱼63吨,十月份比九月份多捕。十月份捕鱼多少吨?
13.菜场运来白菜750千克,运来的萝卜比白菜少,运来萝卜多少千克?
14.本场数学考试的时间为90分钟,当你做到这一题时,时间大约过去了,如果剩下的题目解答还需要的时间,那么做完整张试卷后检查的时间约占总时间的几分之几?约为多少分钟?
15.赵老师家到学校的路程是千米,他先骑车行了全程的到达商店,此时距离学校还有多远?(请先在图中用“△”标出商店的大致位置,再解答题目)
16.深圳,简称“深”,别称“鹏城”,中国四大一线城市之一,是国际科技产业创新中心。全市面积大约2000平方千米,其中宝安区面积最大,约占全市面积的,盐田区面积最小,约占全市面积的。宝安区和盐田区的面积大约各是多少平方千米?
17.爸爸今年36岁,我今年的年龄是爸爸年龄的,是爷爷年龄的。爷爷今年多少岁?
18.信辉小区有三个快递网点:申通快递、顺丰快递、韵达快递,申通快递网点的人数是顺丰快递的,韵达快递网点人数是顺丰快递的,申通快递网点有20人,韵达快递网点有多少人?
19.下图的总面积是156平方厘米,两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,大、小长方形面积的比是多少?大长方形面积是多少?
20.六(1)班、六(2)班学生数的比是7∶8,如果从六(2)班调8人到六(1)班,则六(1)班、六(2)班学生数的比是5∶4,两班共有多少人?
21.学校合唱社团和舞蹈社团共有56人,舞蹈社团的人数是合唱社团的。合唱社团和舞蹈社团各有多少人?
22.有一个长方体木箱,底面是一个正方形,它的前面和底面的面积比是5∶2。制作这个木箱用了360平方分米的木板,这个长方体木箱的底面积是多少平方分米?(木板的厚度和接头处忽略不计)
23.航模比赛,学校买来184架飞机模型,按1∶3∶4的比例分给四、五、六年级,每个年级各分得多少架飞机模型?
24.甲、乙两地相距240千米,A、B两辆汽车同时从甲、乙两地相对开出,1.5小时相遇,A、B两辆汽车的速度比是3∶5,A、B两辆汽车平均每小时分别行多少千米?
参考答案:
1.水深:1.5米;抹水泥面积320平方米
【详解】288÷(24×8)=1.5(米)
(24×2+8×2)×2+24×8=320(平方米)
2.36升
【分析】根据题意可知,把铁块放入玻璃缸中,溢出水的体积等于铁块的体积减去玻璃缸内无水部分的体积,根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,把数据代入公式解答。
【详解】4×4×4-8×7×(6-5.5)
=64-56×0.5
=64-28
=36(立方分米)
36立方分米=36升
答:缸里的水溢出36升。
【点睛】此题主要考查正方体的体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
3.3.75厘米
【详解】10-20×10×25÷(40×20)=3.75(厘米)
4.(1)1750平方米;(2)2090平方米;(3)2800立方米。
【分析】(1)求这个游泳池的占地面积,只与游泳池的底面面积有关,利用长方形的面积公式:长×宽即可解决。
(2)在游泳池底面和四壁抹水泥即没有上面,只有5个面,根据公式:长×宽+(长×高+宽×高)×2即可求解。
(3)根据长方体的体积公式:长×宽×高即可求解。
【详解】(1)50×35=1750(平方米)
答:这个游泳池占地1750平方米。
(2)50×35+(50×2+35×2)×2
=1750+(100+70)×2
=1750+170×2
=1750+340
=2090(平方米)
答:抹水泥的面积是2090平方米。
(3)50×35×1.6
=1750×1.6
=2800(立方米)
答:水的体积是2800立方米。
【点睛】本题考查长方体的表面积和体积公式,要重点掌握。
5.168升
【分析】求容积的方法和求体积的方法一样,,结果注意单位换算,据此解答。
【详解】
=8×6×(5-1.5)
=48×3.5
=168(立方分米)
168立方分米=168升
答:水箱内的水有168升。
【点睛】本题考查长方体的容积,注意长方体容积的计算方法和体积计算方法一样,结果要换算单位。
6.100立方厘米
【分析】此题考查用“排水法”去求不规则物体的体积。将一个重物放入一个规则的装有水的容器中完全淹没,水面上升,物体排开水的体积,就是物体的体积,这种方法就是排水法。在此题中,土豆的体积就是水上升的体积,就是一个长为10厘米,宽5厘米,高2厘米的长方体体积,根据长方体体积计算公式计算得出答案。
【详解】(cm)
(立方厘米)
答:土豆的体积是100立方厘米。
7.8000块
【分析】先求出铺瓷砖的面积,再用铺瓷砖的面积÷瓷砖面积即可。温泉池没有上面,铺瓷砖的面积=长×宽+长×高×2+宽×高×2,据此列式解答,注意统一单位。
【详解】20×10+20×2×2+10×2×2
=200+80+40
=320(平方米)
2分米=0.2米
320÷(0.2×0.2)
=320÷0.04
=8000(块)
答:共需要8000块这样的瓷砖。
8.44平方分米
【分析】首先搞清这道题是求长方体的侧面积,其次这个长方体的侧面由四个长方形组成,缺少最大的两个面用铁皮最少,也就是缺少前后两个面;只求它的左右、上下4个面的面积之和;据此解答即可。
【详解】3×2×2+2×8×2
=12+32
=44(平方分米)
答:做一节这样的通风管至少需要44平方分米的铁皮。
【点睛】如能画示长方体意图会使题意更加清楚明了,有助于进一步分析和解答。
9.96平方分米
【分析】这个正方体从一个角挖掉一个棱长1分米的正方体,等于这个正方体去掉了3个边长1分米的正方形的面积,又新增加了3个棱长1分米的正方形的面积,与原正方体的表面积相等,由此即可根据正方体的表面积公式:棱长×棱长×6,把数代入即可求解。
【详解】由分析可知,这个立体图形的表面积:
4×4×6
=16×6
=96(平方分米)
答:这个立体图形的表面积是96平方分米。
【点睛】此题主要是考查正方体的表面积,关键明白从这个正方体从一个角挖掉一个棱长1分米的正方体,与原正方体表面积不变。
10.米
【分析】每小时织的长度×相应时间=相应时间织的长度。
【详解】(米)
答:小时织米。
11.吨
【分析】还剩,就是将食堂煤的重量看成单位“1”,则剩下占总质量的,求一个数的几分之几用乘法。
【详解】(吨)
答:还剩吨。
12.81吨
【分析】把九月份捕鱼的吨数看作单位“1”,已知十月份比九月份多捕,那么九月份捕鱼吨数的(1+)就是十月份捕鱼的吨数,用九月份捕鱼的吨数乘(1+)即可求出十月份捕鱼的吨数。
【详解】63×(1+)
=63×
=81(吨)
答:十月份捕鱼81吨。
13.300千克
【分析】把白菜的质量看作单位“1”,已知运来的萝卜比白菜少,那么运来的萝卜就是白菜的(1-),用白菜的质量乘(1-)即可解答。
【详解】750×(1-)
=750×
=300(千克)
答:运来的萝卜有300千克。
14.;13.5分钟
【分析】把总时间看作单位“1”,根据分数减法的意义,用1--即可求出做完整张试卷后检查的时间约占总时间的几分之几;根据分数乘法的意义,用总时间乘(1--)即可求出做完整张试卷后检查的时间。
【详解】1--=
90×=13.5(分钟)
答:做完整张试卷后检查的时间约占总时间的;约为13.5分钟。
15.千米;图见详解
【分析】根据求一个数的几分之几是多少,用乘法计算,用乘法计算出商店的位置,再用全长减去赵老师骑到商店的路程,即可求出剩下的路程;再从赵老师家往学校方向大约在全长的用标出“△”即可。
【详解】×=(千米)
-=(千米)
作图如下:
答:此时距离学校还有千米。
16.400平方千米;75平方千米
【分析】从“占全市面积的,全市面积的”可知,以全市面积为单位“1”,根据求一个数的几分之几,用乘法计算。分别用全市面积×对应分率,即可求出宝安区和盐田区的面积。据此解答。
【详解】宝安区:2000×=400(平方千米)
盐田区:2000×=75(平方千米)
答:宝安区的面积大约是400平方千米,盐田区的面积大约各是75平方千米。
17.72岁
【分析】把爸爸今年的年龄看作单位“1”, 我今年的年龄是爸爸年龄的,用爸爸今年的年龄×,求出我今年的年龄,再把爷爷今年的年龄看作单位“1”,爷爷年龄的,对应的是我今年的年龄,求爷爷今年的年龄,用我今年的年龄÷,即可解答。
【详解】36×÷
=6÷
=6×12
=72(岁)
答:爷爷今年72岁。
18.12人
【分析】已知申通快递网点有20人,是顺丰快递的,把顺丰快递的人数看作单位“1”,单位“1”未知,用申通快递网点的人数除以,求出顺丰快递的人数;
已知韵达快递网点人数是顺丰快递的,把顺丰快递的人数看作单位“1”,单位“1”已知,用顺丰快递的人数乘,求出韵达快递网点的人数。
【详解】20÷×
=20××
=30×
=12(人)
答:韵达快递网点有12人。
19.4∶3;96平方厘米
【分析】(1)设重叠部分的面积是1,先把大长方形的面积看成单位“1”,它的对应数量是重叠部分的面积,由此用除法求出大长方形的面积;同理把小长方形的面积看成单位“1”,它的对应数量是重叠部分的面积,由此用除法求出小长方形的面积;然后用大长方形的面积比上小长方形的面积即可。
(2)由题意可知,重叠部分的面积是1份,则大长方形的面积是8份,小长方形的面积是6份,大长方形的面积加上小长方形的面积减去重叠部分的面积是8+6-1=13(份),这13份就是图形的总面积,用总面积除以总份数,求出1份是多少,再乘大长方形的份数即可解答。
【详解】1÷=8
1÷=6
8∶6
=(8÷2)∶(6÷2)
=4∶3
156÷(8+6-1)
=156÷13
=12(平方厘米)
12×8=96(平方厘米)
答:大、小长方形面积的比是4∶3,大长方形的面积是96平方厘米。
20.90人
【分析】将两班总人数看作单位“1”,根据六(1)班、六(2)班学生数的比是7∶8,可知原来六(1)班是六(2)班学生数的;从六(2)班调8人到六(1)班,六(1)班是六(2)班学生数的,说明8人的对应分率是(-),根据部分数量÷对应分率=整体数量,即可求出两班总人数。
【详解】8÷(-)
=8÷(-)
=8÷
=8×
=90(人)
答:两班共有90人。
21.32人;24人
【分析】从“舞蹈社团的人数是合唱社团的”可知,舞蹈社团的人数∶合唱社团的人数=3∶4。以合唱社团和舞蹈社团总人数为单位“1”,合唱社团的人数占总人数的。根据求一个数的几分之几是多少,用乘法计算,用总人数×即可求出合唱社团的人数,再用总人数-合唱社团的人数,即可求出舞蹈社团的人数。据此解答。
【详解】=3∶4
合唱社团的人数:
56×
=56×
=32(人)
舞蹈社团:56-32=24(人)
答:合唱社团有32人,舞蹈社团有24人。
22.30平方分米
【分析】
长方体一般情况下六个面都是长方形,特殊情况时有两个面是正方形,其他四个面都是长方形,并且这四个面完全相同。如图,这个长方体木箱前后左右4个面完全一样,上下面是完全一样的正方形,它的前面和底面的面积比是5∶2,因此前后左右4个面和上下两个面的比是(5×4)∶(2×2),表面积÷总份数,求出一份数,一份数×底面对应份数=底面积,据此列式解答。
【详解】360÷(5×4+2×2)×2
=360÷(20+4)×2
=360÷24×2
=15×2
=30(平方分米)
答:这个长方体木箱的底面积是30平方分米。
23.四年级分得23架飞机模型,五年级分得69架飞机模型,六年级分得92架飞机模型。
【分析】已知模型飞机的总数,和分配比例,用总数量除以总份数,和所占份数就等于一个年级分得飞机模型的数量,据此解答。
【详解】总份数:1+3+4=8
四年级:184÷8×1=23(架)
五年级:184÷8×3
=23×3
=69(架)
六年级:184÷8×4
=23×4
=92(架)
答:四、五、六年级,每个年级各分得23架、69架、92架飞机模型。
24.60千米;100千米
【分析】根据速度和=总路程÷相遇时间,求出两车速度和,将比的前后项看成份数,速度和÷总份数,求出一份数,一份数分别乘A、B两车对应分率,即可求出A、B两车速度。
【详解】240÷1.5÷(3+5)
=160÷8
=20(千米)
20×3=60(千米/小时)
20×5=100(千米/小时)
答:A辆汽车平均每小时行60千米,B辆汽车平均每小时行100千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
