6.1图形认识 课件(共20张PPT) 青岛版(2024)数学七年级上册
文档属性
| 名称 | 6.1图形认识 课件(共20张PPT) 青岛版(2024)数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 352.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
6.1图形的认识
第6章 基本的几何图形
1.我能在具体实物中认识圆柱、圆锥、棱柱、棱锥、球,感受丰富多彩的图形世界;
2.我能从具体实物中抽象出几何体的概念,并能描述它们的特征;
3.结合实际创造活跃、有趣的情景,提高学习兴趣,在活动中获得成功的体验,培养探索精神树立学习信心。
学习目标
是它的形状(如方的,圆的等)、大小(如长度、面积、体积等)和位置关系(如相交、垂直、平行等)而它们的颜色、质量、材料等则是其他学科所关注的。这时我们得到的就是各种几何体,简称体。
思考:对于各种各样的物体,数学中关注的是什么?
观察与发现(一)
思考我们生活中见到的橡皮、魔方、足球、茶叶桶、漏斗,这些物品个具有什么样的形状?
对于我们看到的物体,只研究它们的 、________和位置关系,而不考虑 、 、________等其他性质时,就得到各种几何体,几何体简称为 。
长方体、正方体、球、圆柱、圆锥
大小
形状
质量
原料
颜色
体
1.体是由面围成的。
例如,长方体是由_____个____面 围成;
圆锥是由_____个_____面和_____个______面围成;
球是由______个_______面围成。
六
平
一
曲
一
平
一
曲
思考与交流(二)
2.镜面、黑板、操场、平静的湖面等,都给我们以平面的想象,就是数学上说的 。
你发现了平面有什么特点?
生活中除了平面的形象外,我们还会经常遇到哪些曲面的形象。想想生活中曲面的形象,你能举出一些曲面的例子吗?
水杯、鼠标、花盆等
平面没有厚薄,没有边界,是向四面八方无限延展的。
平面
3.几何图形
立体 图形 定义 点不都在__ __的几何图形
举例 长方体、正方体、圆柱、圆锥、球等
平面 图形 定义 点都在______________的几何图形
举例 线段、角、三角形、圆、长方形、
正方形等
同一个平面内
同一个平面内
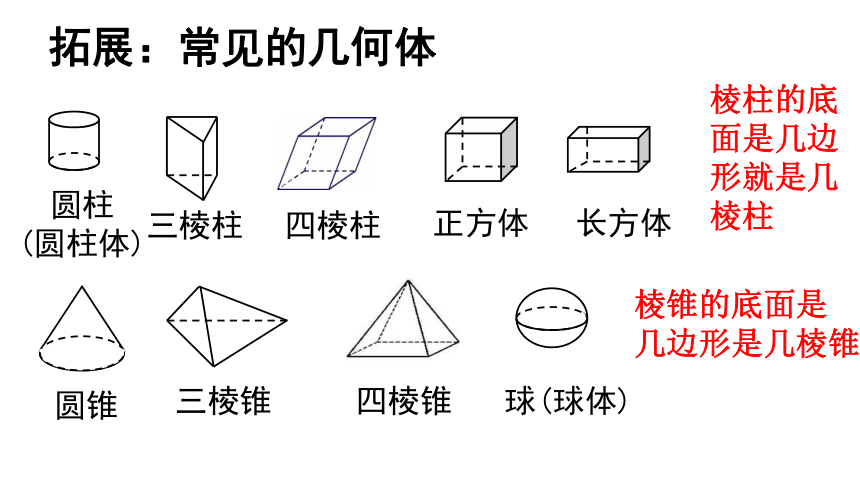
正方体
长方体
三棱柱
圆柱
(圆柱体)
三棱锥
圆锥
球(球体)
拓展:常见的几何体
四棱柱
四棱锥
棱柱的底面是几边形就是几棱柱
棱锥的底面是
几边形是几棱锥
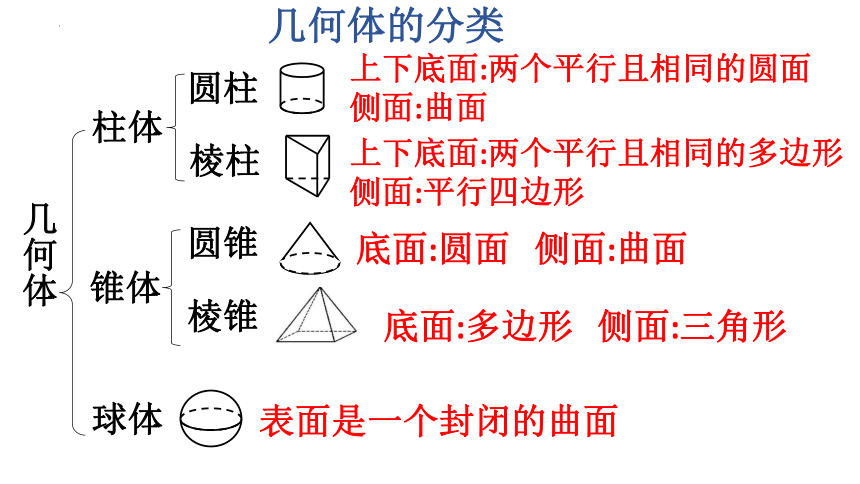
柱体
锥体
几何体的分类
上下底面:两个平行且相同的圆面
侧面:曲面
上下底面:两个平行且相同的多边形
侧面:平行四边形
底面:圆面 侧面:曲面
底面:多边形 侧面:三角形
表面是一个封闭的曲面
圆柱
棱柱
圆锥
几何体
球体
棱锥
均是平面
既有平面
也有曲面
几何体的分类 2
圆柱
棱柱
圆锥
均是曲面
棱锥
几何体
(围成几何体的面)
球体
点动成线
面动成体
线动成面
A
O
A
A
A'
点、线、面的关系
天上的星星给我们以______的形象;
划过夜空的流星给我们以_____________的形象;
打开折扇时,随着扇骨的转动形成一个扇面,给我们以___________的形象;
当宾馆的旋转门旋转时,给我们以__________的形象。
点
点动成线
线动成面
面动成体
例
1.____、____、____、____以及它们的组合都是几何图形.如果一个几何图形上的点 ,那么这样的几何图形叫做立体图形。
如果一个几何图形上的所有点 ,那么这样的几何图形叫做平面图形。
点
线
面
体
不都在同一平面内
都在同一平面内
拓展延伸
多面体指四个或四个以上多边形所围成的立体图形。 特征:各面都是平面的立体图形称为多面体
例题:下列立体图形中,是多面体的是( )
A
B
C
D
B
课堂巩固
圆柱
圆锥
三棱锥
长方体
球
正方体
1.写出下列图形的具体名字
2. 如图所示的几何图形中,属于圆锥的是( )
3. 在下列立体图形中,只要两个面就围成的是( )A.长方体 B.圆柱体C.圆锥体 D.球
A
B
C
D
D
C
4.下列几何体属于柱体的个数是( )
A.3 B.4 C.5 D.6
D
4.下面的平面图形绕轴旋转一周,可以得到下面的立体图形.用线将上面的平面图形与对应的立体图形连接起来.
5.指出如图所示的几何体中的柱体、锥体和球,并试着用另一种分类方式进行分类
按围成的面分为:
全是平面:①②⑤⑥⑦
既有平面又有曲面:④⑧
全是曲面:③
1.几何体的分类以及每一种分类的特征
2.构成我们常见的几何体的面有三种情况
3.多面体指四个或四个以上多边形所围成的立体图形
课堂小结
6.1图形的认识
第6章 基本的几何图形
1.我能在具体实物中认识圆柱、圆锥、棱柱、棱锥、球,感受丰富多彩的图形世界;
2.我能从具体实物中抽象出几何体的概念,并能描述它们的特征;
3.结合实际创造活跃、有趣的情景,提高学习兴趣,在活动中获得成功的体验,培养探索精神树立学习信心。
学习目标
是它的形状(如方的,圆的等)、大小(如长度、面积、体积等)和位置关系(如相交、垂直、平行等)而它们的颜色、质量、材料等则是其他学科所关注的。这时我们得到的就是各种几何体,简称体。
思考:对于各种各样的物体,数学中关注的是什么?
观察与发现(一)
思考我们生活中见到的橡皮、魔方、足球、茶叶桶、漏斗,这些物品个具有什么样的形状?
对于我们看到的物体,只研究它们的 、________和位置关系,而不考虑 、 、________等其他性质时,就得到各种几何体,几何体简称为 。
长方体、正方体、球、圆柱、圆锥
大小
形状
质量
原料
颜色
体
1.体是由面围成的。
例如,长方体是由_____个____面 围成;
圆锥是由_____个_____面和_____个______面围成;
球是由______个_______面围成。
六
平
一
曲
一
平
一
曲
思考与交流(二)
2.镜面、黑板、操场、平静的湖面等,都给我们以平面的想象,就是数学上说的 。
你发现了平面有什么特点?
生活中除了平面的形象外,我们还会经常遇到哪些曲面的形象。想想生活中曲面的形象,你能举出一些曲面的例子吗?
水杯、鼠标、花盆等
平面没有厚薄,没有边界,是向四面八方无限延展的。
平面
3.几何图形
立体 图形 定义 点不都在__ __的几何图形
举例 长方体、正方体、圆柱、圆锥、球等
平面 图形 定义 点都在______________的几何图形
举例 线段、角、三角形、圆、长方形、
正方形等
同一个平面内
同一个平面内
正方体
长方体
三棱柱
圆柱
(圆柱体)
三棱锥
圆锥
球(球体)
拓展:常见的几何体
四棱柱
四棱锥
棱柱的底面是几边形就是几棱柱
棱锥的底面是
几边形是几棱锥
柱体
锥体
几何体的分类
上下底面:两个平行且相同的圆面
侧面:曲面
上下底面:两个平行且相同的多边形
侧面:平行四边形
底面:圆面 侧面:曲面
底面:多边形 侧面:三角形
表面是一个封闭的曲面
圆柱
棱柱
圆锥
几何体
球体
棱锥
均是平面
既有平面
也有曲面
几何体的分类 2
圆柱
棱柱
圆锥
均是曲面
棱锥
几何体
(围成几何体的面)
球体
点动成线
面动成体
线动成面
A
O
A
A
A'
点、线、面的关系
天上的星星给我们以______的形象;
划过夜空的流星给我们以_____________的形象;
打开折扇时,随着扇骨的转动形成一个扇面,给我们以___________的形象;
当宾馆的旋转门旋转时,给我们以__________的形象。
点
点动成线
线动成面
面动成体
例
1.____、____、____、____以及它们的组合都是几何图形.如果一个几何图形上的点 ,那么这样的几何图形叫做立体图形。
如果一个几何图形上的所有点 ,那么这样的几何图形叫做平面图形。
点
线
面
体
不都在同一平面内
都在同一平面内
拓展延伸
多面体指四个或四个以上多边形所围成的立体图形。 特征:各面都是平面的立体图形称为多面体
例题:下列立体图形中,是多面体的是( )
A
B
C
D
B
课堂巩固
圆柱
圆锥
三棱锥
长方体
球
正方体
1.写出下列图形的具体名字
2. 如图所示的几何图形中,属于圆锥的是( )
3. 在下列立体图形中,只要两个面就围成的是( )A.长方体 B.圆柱体C.圆锥体 D.球
A
B
C
D
D
C
4.下列几何体属于柱体的个数是( )
A.3 B.4 C.5 D.6
D
4.下面的平面图形绕轴旋转一周,可以得到下面的立体图形.用线将上面的平面图形与对应的立体图形连接起来.
5.指出如图所示的几何体中的柱体、锥体和球,并试着用另一种分类方式进行分类
按围成的面分为:
全是平面:①②⑤⑥⑦
既有平面又有曲面:④⑧
全是曲面:③
1.几何体的分类以及每一种分类的特征
2.构成我们常见的几何体的面有三种情况
3.多面体指四个或四个以上多边形所围成的立体图形
课堂小结
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
