勾股定理整理与复习

(共45张PPT)
勾股定理整理与复习
深圳市罗湖区翠园初级中学 黄缨 整理
实际问题
（判定直角三角形）
实际问题
（直角三角形边长计算）
勾股定理
勾股定理的逆定理
知识结构图
再回首
A
B
C
勾a
股b
弦c
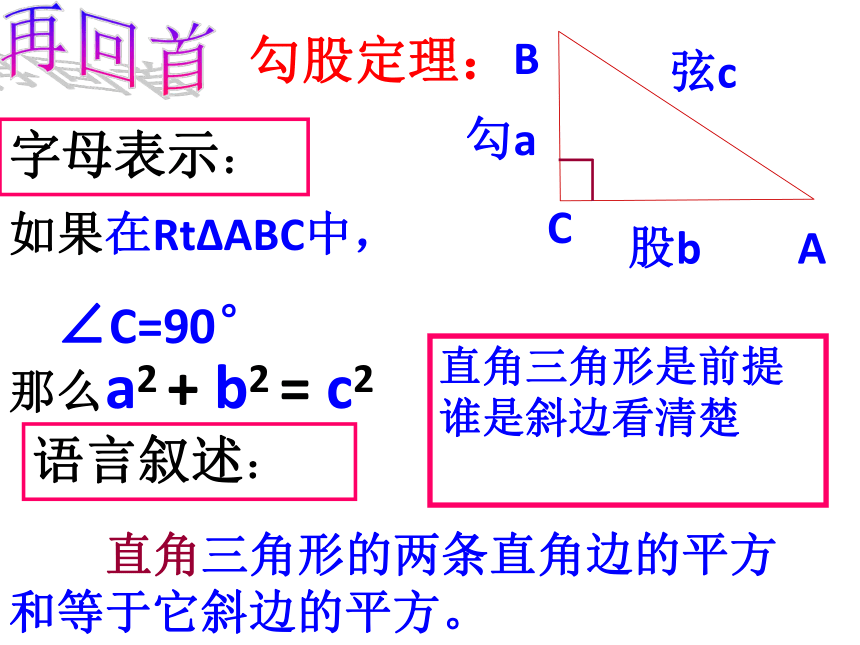
勾股定理：
直角三角形的两条直角边的平方和等于它斜边的平方。
那么a2 + b2 = c2
如果在Rt ABC中，
∠C=90°
语言叙述：
字母表示：
直角三角形是前提
谁是斜边看清楚
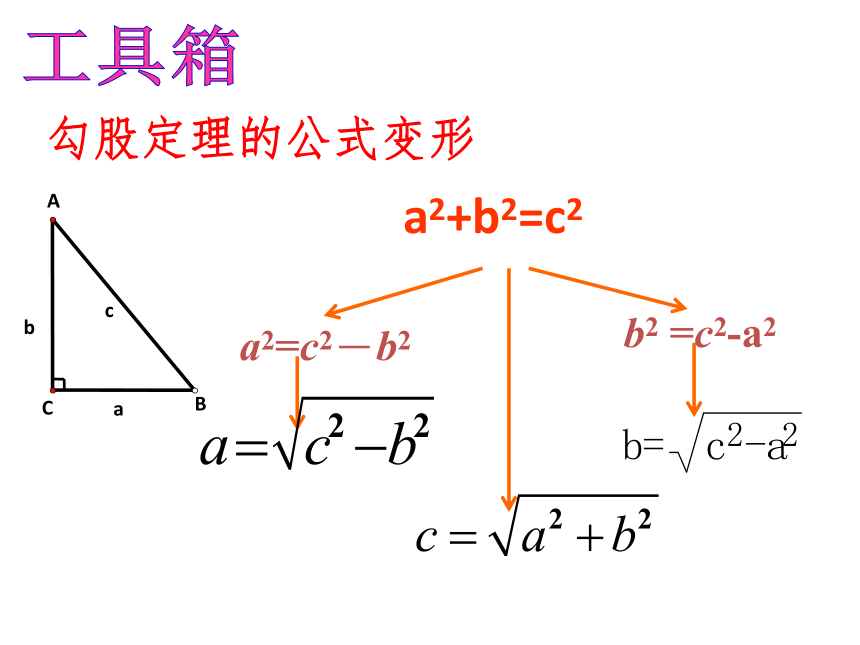
勾股定理的公式变形
工具箱
a2=c2－b2
b2 =c2-a2
a2+b2=c2
c
b
a
C
B
A
2.勾股定理的逆定理:
知识回顾
1.勾股定理：如果直角三角形的两直角边长分别为a、b, 斜边长为c, 那么a2+b2=c2.
c
a
b
C
A
B
┓
∵∠C=90°
∴ a2+b2=c2
或 ∴ BC2+AC2=AB2
三角形的三边a,b,c 满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.其中满足a2+b2=c2的三个正整数，称为勾股数。
在 ABC中, a，b，c为三边长,其中 c为最大边, 若a2 +b2=c2, 则 ABC为直角三角形; 若a2 +b2>c2, 则 ABC为锐角三角形; 若a2 +b24、特殊三角形的三边关系：
若∠A=30°，则
若∠A=45°，则
3、常用的勾股数：
① 3、4、5； ② 5、12、13； ③ 7、24、25； ④ 8、15、17； ⑤ 9、40、41.
知识回顾
1.在Rt△ABC中，∠C=90°.
（1）如果a=3，b=4， 则c=　 ；
（2）如果a=6，c=10， 则b=　 ；
（3）已知b=3，∠A=30°，则a= ，c= .
（4）已知∠Ａ＝４５°，ｃ＝８，则ａ= ，ｂ= 。
（5）已知ａ：ｂ＝３：４，ｃ＝２５，则ａ= ，ｂ= 。
（6）在Rt△ABC中，∠C=90°，若a=12,c-b=8,则b= ,c= .
5
8
题型一 勾股定理的直接应用
2.已知在△ABC 中，∠B =90°，一直角边为a，斜边为b，则另一直角边c满足c2 = .
20
15
13
5
A
B
D
C
3.如图，等边三角形的边长是6，求这个三角形的面积。
变式：等边三角形ABC的面积为 ，求这个三角形的边长？
归纳：等腰三角形的顶角平分线、底边上的高、底边上的中线都能把等腰三角形分为两个全等的直角三角形。注意到这一点后，一些与等腰三角形有关的问题可以用勾股定理来解决。
S1
S2
S3
S4
1
2
3
4
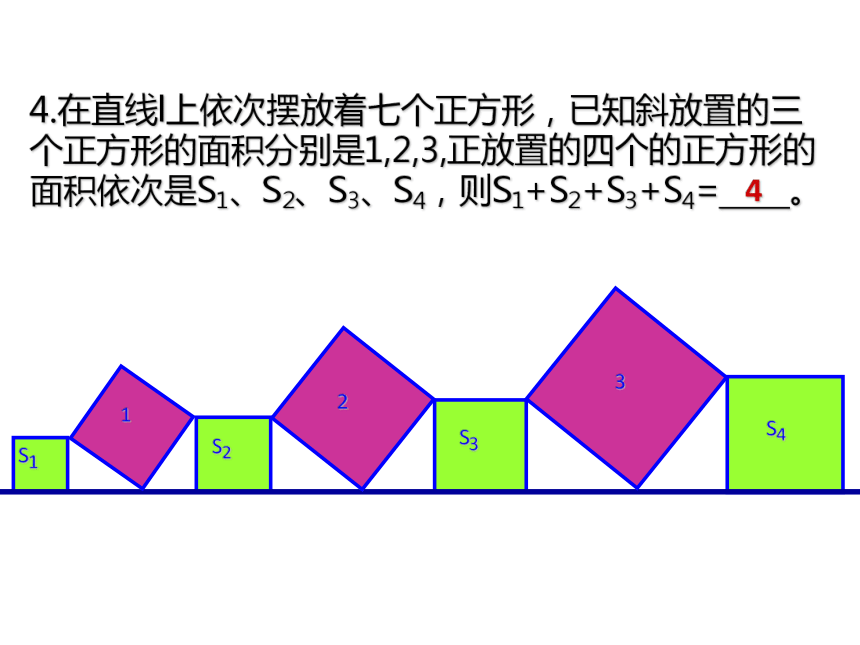
4.在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个的正方形的面积依次是S1、S2、S3、S4，则S1+S2+S3+S4= 。
2.已知：在△ABC中，AB＝15 cm，AC＝13 cm，高AD＝12 cm，求S△ABC．
图1
图2
答案：第1种情况：如图1，在Rt△ADB和Rt△ADC中，分别由勾股定理，得BD＝9，CD＝5，所以BC＝BD+ CD＝9+5＝14．故S△ABC＝84（cm2）．
第2种情况，如图2，可得：S△ABC=24（ cm2 ）．
题型二 分类讨论问题
1.已知一个直角三角形的两条边长是3 cm和4 cm，则第三条边的长为 ．
5 cm或 cm
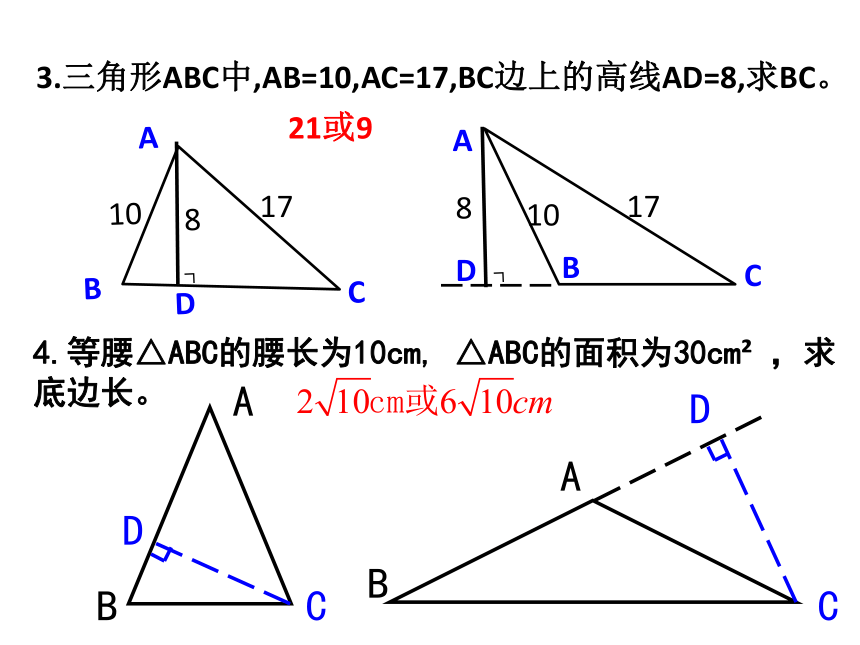
3.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC。
∟
D
∟
D
A
B
C
A
B
C
10
17
8
17
10
8
4.等腰△ABC的腰长为10cm, △ABC的面积为30cm ，求底边长。
A
D
B
C
C
D
A
B
21或9
规律
1.直角三角形中，已知两边长是直角边、斜边不知道时，应分类讨论。
2.当已知条件中没有给出图形时，应认真读句画图，避免遗漏另一种情况。
1.如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北11km处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？
A
B
小河
东
北
牧童
小屋
题型三 勾股定理的实际应用
分析：最短的路线是从A点垂直走到河边，再直奔B点。
解：
2.某校A与直线公路距离为3000米，又与该公路的某车站D的距离为5000米，现在要在公路边建一小商店C，使之与该校A及车站D的距离相等，求商店与车站D的距离。
A
B
C
D
3000
5000
4000
x
4000-x
x
3125米
C
3.如图，一条河同一侧的两村庄A、B，其中A、B到河岸最短距离分别为AC=1km，BD=2km，CD=4cm，现欲在河岸上建一个水泵站向A、B两村送水，当建在河岸上何处时，使到A、B两村铺设水管总长度最短，并求出最短距离。
A
P
B
A′
D
E
1
2
4
1
1
4
5km
4.如图，∠B=∠C=∠D=∠E=90°，且AB=CD=3，BC=4，DE=EF=2，则求AF的长。
A
B
C
D
E
F
3
3
4
2
2
3
2
4
2
10
思考：利用勾股定理解题决实际问题时，基本步骤是什么？
1.把实际问题转化成数学问题，找出相应的直角三角形.
2.在直角三角形中找出直角边，斜边.
3.根据已知和所求，利用勾股定理解决问题.
1.已知：如图，AD是△ABC的高，AB=10，AD=8，BC=12 .
求证： △ABC是等腰三角形.
答案：证明：∵AD是△ABC的高，∴∠ADB=∠ADC=90°.∵在Rt△ADB中，AB=10，AD=8，∴BD=6 .∵BC=12, ∴DC=6.∵在Rt△ADC中，AD=8，∴AC=10，∴AB=AC.即△ABC是等腰三角形.
分析：利用勾股定理求出线段BD的长，也能求出线段AC的长，最后得出AB=AC，即可.
题型四 勾股定理的综合应用
2.已知：如图，在△ABC中，∠B=45°，∠C=60°，AB=2.
求（1）BC 的长；（2）S△ABC .
分析：由于本题中的△ABC不是直角三角形，所以添加BC边上的高这条辅助线，就可以求得BC及S△ABC .
答案：过点A作AD⊥BC于D,∴∠ADB=∠ADC=90°.
在△ABD中，∠ADB=90°，
∠B=45°，AB=2，∴AD=BD= .∵在△ABD中，∠ADC=90°，∠C=60°，AD= ，
∴CD= ,∴BC= ，S△ABC =
思考：利用勾股定理解决综合题的基本步骤是什么？
1.画图与标图，根据题目要求添加辅助线，构造直角三角形.
2.将已知量与未知量集中到同一个直角三角形中.
3 .利用勾股定理列出方程.
4.解方程，求线段长，最后完成解题.
1. 判断下列命题：
①等腰三角形是轴对称图形；②若a>1且b>1，则a+b>2；③角平分线上的点到角的两边距离相等；④直角三角形的两锐角互余,其中逆命题正确的有( )
A.1个 B.2个 C.3个 D.0个
题型五 勾股定理的逆定理的直接应用
2.已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的
最大角是＿＿度;斜边上的高为 ；面积为 。
90
B
54
直角三角形
3．如果△ABC的三边分别为a、b、c且满足a2＋b2＋c2＋50＝6a＋8b＋10c，判定△ABC的形状.
a
b
h
c
其中正确结论的是 。
5.直角三角形的两条直角边长为a,b,斜边为c，斜边上的高为h, 下列说法：
①a2,b2,c2能组成一个三角形
② , , 能组成一个三角形
④ , , 能组成直角三角形
③c+h,a+b,h能组成直角三角形
4.已知△ABC的三条边长分别为a、b、c，且满足关系：
(a+b)2 + c2 = 3ab + c(a+b),试判断△ABC的形状，并说明理由.
等边三角形
②③④
6.△ABC三边a,b,c为边向外作正方形、等边三角形，以三边为直径作半圆，若S1+S2=S3成立，则△ABC是直角三角形吗？
A
B
C
a
b
c
S1
S2
S3
A
C
a
b
c
S1
S2
S3
B
S2
S3
S1
C
B
A



1.已知三角形ABC中，AB=10，BC=21，AC=17，求BC边上的高线AD.
A
B
C
D
解：设BD=X，则DC=21－X。
∵AD⊥BC
∴AD2=AB2-BD2=102-X2
AD2=AC2-CD2=172-（21-X）2
解得X=6
∴102-X2=172-（21-X）2
∴AD2=102-62=64
∴AD=8
题型六 方程思想
2.等腰三角形底边上的高为8，周长为32，则三角形的面积为（ ）
A、56 B、48 C、40 D、32
A
B
C
D
8
x
x
16-x
x2+82=(16-x)2
x=6
BC=2x=12
B
3.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm，则Rt△ABC的面积是（ ）
A.24cm2 B.36cm2 C.48cm2 D.60cm2
C
A
B
a
b
c
a+b=14
c=10
a2+b2=102=100
(a+b)2=142=196
2ab=(a+b)2-(a2+b2)
=196-100
=96
A
直角三角形中，当无法已知两边求第三边时，应采用间接求法：灵活地寻找题中的等量关系，利用勾股定理列方程。
规律
1.如图，小颍同学折叠一个直角三角形的纸片，使A与B重合，折痕为DE，若已知AC=10cm，BC=6cm,你能求出CE的长吗？
C
A
B
D
E
x
10-x
6
10-x
题型七 折叠问题
2.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM。求：
（1）CF； （2）EC；（3）AE。
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
B
C
D
E
F
8
10
10
X
8-X
8-X
6
4
解：由题意得AD= BC=10cm
∴BF2=AF2-AB2=102-82
在直角三角形EFC中FC2+EC2=EF2
解得X=3
∴BF=6,FC=4
∵AB⊥BC
设EC=X，则EF=8－X。
即42+X2=（8-X）2
∴EC=3
3.折叠长方形纸片，先折出折痕对角线BD，在绕点D折叠，使点A落在BD的E处，折痕DG，若AB=4，BC=3，求AG的长。
D
A
G
B
C
E
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗？
3.折叠长方形纸片，先折出折痕对角线BD，在绕点D折叠，使点A落在BD的E处，折痕DG，若AB=4，BC=3，求AG的长。
D
A
G
B
C
E
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗？
1.如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是多少？
20
3
2
A
B
２０
２
3
2
3
2
3
Ａ
Ｂ
Ｃ
∵ AB2=AC2+BC2=625,
∴ AB=25.
题型八 展开思想


B
B
8
O
A
2
蛋糕
A
C
2.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3）是( )
A.20cm B.10cm C.14cm D.无法确定
B
８
６
3.正方体的棱长为５cm，一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物，那么它爬行的最短路程的长是多少？
A
B
C
D′
A′
B′
C′
D
4.在长30cm、宽50 cm、高40 cm的木箱中，如果在箱内的A处有一只昆虫，它要在箱壁上爬行到B处，至少要爬多远？
C
D
A
.
B
.
30
50
40
图①
30
50
40
C
D
A
.
B
.
A
D
C
B
30
50
40
C
C
D
A
.
B
.
A
C
B
D
图②
30
40
50
30
40
50
C
C
D
A
.
B
.
图③
50
A
D
C
B
40
30
30
40
50
1. 几何体的表面路径最短的问题，一般展开表面成平面。
2.利用两点之间线段最短，及勾股定理求解。
规律
已知：如图，四边形ABCD，AB=1，BC=2，CD=2，AD=3， 且AB⊥BC.求四边形 ABCD的面积.
分析：本题解题的关键是恰当的添加辅助线，利用勾股定理的逆定理判定△ADC的形状为直角三角形，再利用勾股定理解题.
答案：连接AC,∵AB⊥BC，∴∠ABC=90°.
∵在△ABC中，∠ABC=90°，AB=1，BC=2，
∴AC= . ∵CD=2，AD=3, ∴△ACD是直角三角形；∴四边形的面积为 .
题型九 勾股定理及其逆定理的综合应用
1.如图，在△ABC中，AB=AC，D点在CB延长线上，求证：
AD2-AB2=BD·CD
A
B
C
D
证明：
过A作AE⊥BC于E
E
∵AB=AC，∴BE=CE
在Rt △ADE中，
AD2=AE2+DE2
在Rt △ABE中，
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
题型十 综合证明题
A
M
N
P
Q
30°
B
D
160
80
E
100
60
60
100
2.如图，公路MN和小路PQ在P处汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响 如果学校受到影响,那么受影响将持续多长时间
24秒
3.某风景区有2个景点A、B(B位于A的正东方),为了方便游客，风景区管理处决定在相距2千米的A、B两景点之间修一条笔直的公路(即图中的线段AB),经测量，在点A 的北偏东60°方向、点B的北偏西45°方向的C处有一个半径为0.7千米的小水潭，问小水潭会不会影响公路的修筑，为什么？
（参考数据： ）
C
A
B
D
60°
45°
30°
45°
x
x
声明：本课件部分内容来源于21世纪教育网