八上数学：1.1.2-验证勾股定理

(共26张PPT)
1.1 探索勾股定理
第一章 勾股定理
导入新课
讲授新课
当堂练习
课堂小结
第2课时 验证勾股定理
1.学会用几种方法验证勾股定理．（重点）
2.能够运用勾股定理解决简单问题．（重点，难点）
学习目标
导入新课
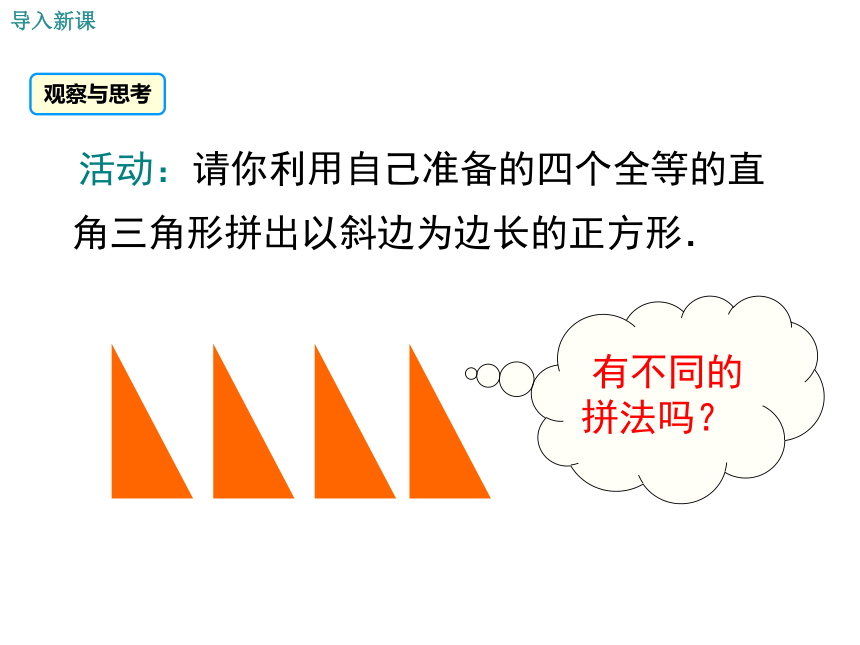
观察与思考
活动：请你利用自己准备的四个全等的直角三角形拼出以斜边为边长的正方形．
有不同的拼法吗？
讲授新课
勾股定理的验证
一
据不完全统计，验证的方法有400多种，你有自己的方法吗？
问题：上节课我们认识了勾股定理，你还记得它的内容吗？那么如何验证勾股定理呢 ？
双击图标
a
a
a
a
b
b
b
b
c
c
c
c
方法小结：我们利用拼图的方法，将形的问题与数的问题结合起来，再进行整式运算，从理论上验证了勾股定理．
验证方法一：毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
c
a
b
c
a
b
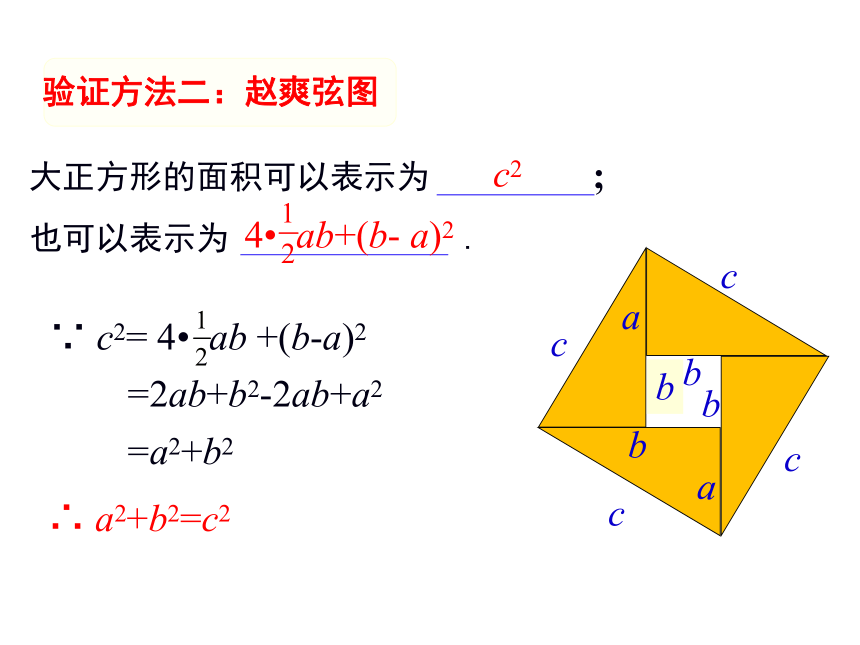
验证方法二：赵爽弦图
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b- a)2
b
c
a
b
c
a
A
B
C
D
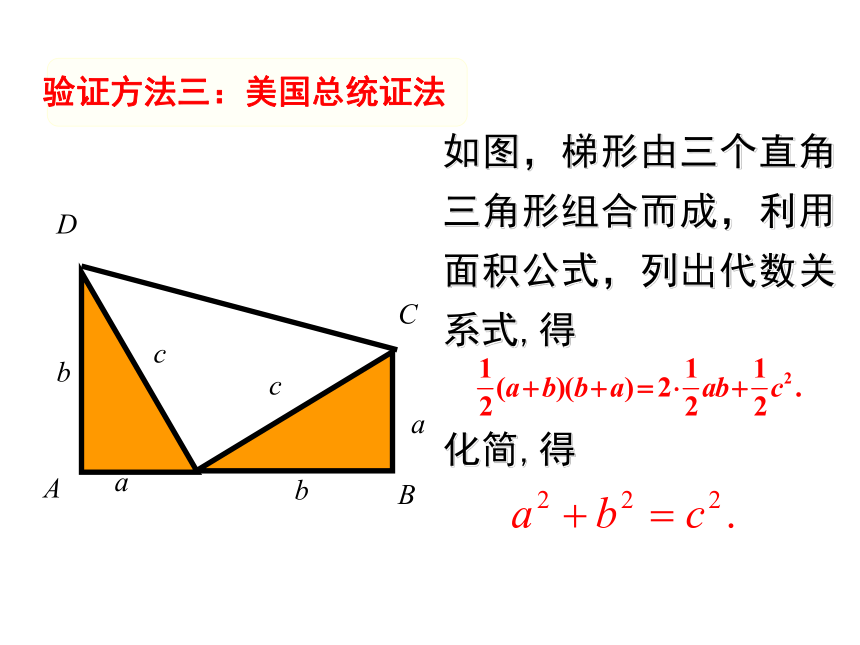
如图，梯形由三个直角三角形组合而成，利用面积公式，列出代数关系式,得
化简,得
验证方法三：美国总统证法
a
b
c
青入
青方
青
出
青出
青入
朱入
朱方
朱出
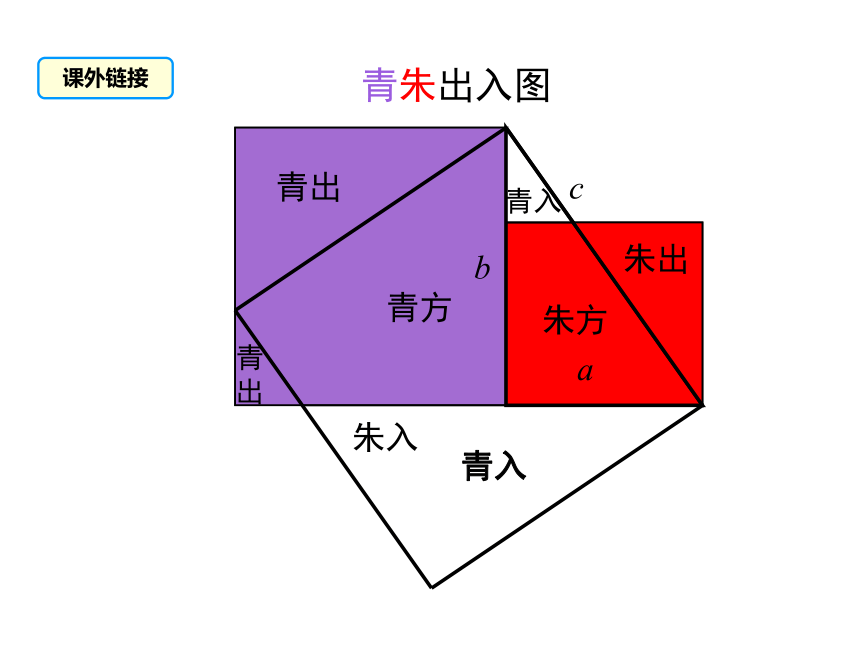
青朱出入图
课外链接
a
b
c
A
B
C
D
E
F
O
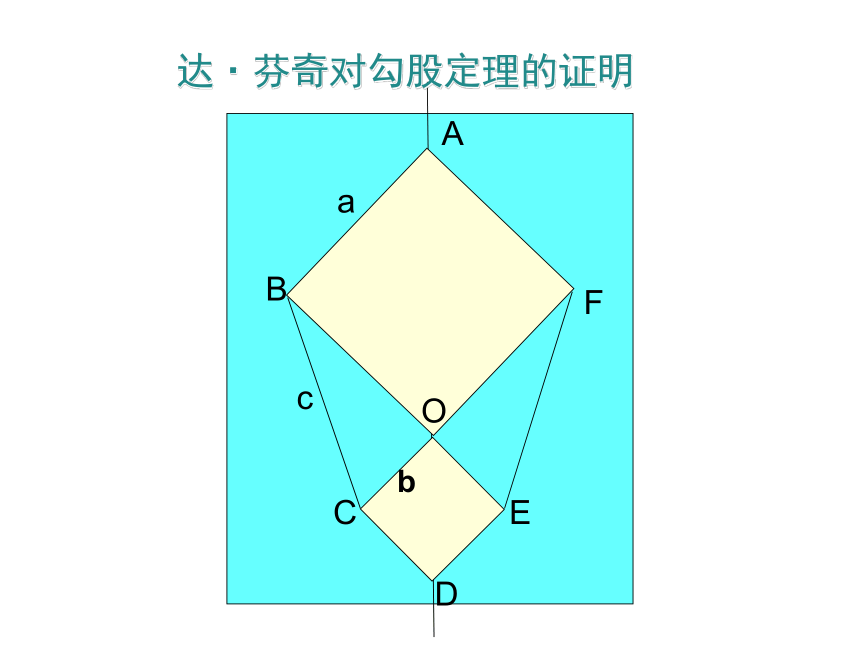
达·芬奇对勾股定理的证明
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
如图，过 A 点画一直线 AL 使其垂直于 DE， 并交 DE 于 L，交 BC 于 M.通过证明△BCF≌△BDA，利用三角形面积与长方形面积的关系，得到正方形ABFG与矩形BDLM等积，同理正方形ACKH与 矩形MLEC也等积，于是推得
欧几里得证明勾股定理
推荐书目
议一议
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.
勾股定理的简单应用
二
例1：我方侦查员小王在距离东西向公路400m处侦查，发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪，测得汽车与他相距400m,10s后，汽车与他相距500m，你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理，得AB2=BC2+AC2，
即 5002=BC2+4002，
所以，BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000（m）
即它行驶的速度为108km/h.
练一练
1.湖的两端有A、Ｂ两点，从与ＢA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为（ )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120

A
A
B
C
2.如图,太阳能热水器的支架AB长为90 cm,与AB垂直的BC长为120 cm.太阳能真空管AC有多长
解：在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2，
AC2=902+1202，
AC=150(cm).
答:太阳能真空管AC长150 cm.
例2：如图，高速公路的同侧有A，B两个村庄，它们到高速公路所在直线MN的距离分别为AA1＝2km，BB1＝4km，A1B1＝8km.现要在高速公路上A1、B1之间设一个出口P，使A，B两个村庄到P的距离之和最短，求这个最短距离和．
解：作点B关于MN的对称
点B′，连接AB′，交A1B1于
P点，连BP.
则AP＋BP＝AP＋PB′＝AB′，
易知P点即为到点A，B距离之和最短的点．
过点A作AE⊥BB′于点E，
则AE＝A1B1＝8km，B′E＝AA1＋BB1＝2＋4＝6(km)．
由勾股定理，得B′A2＝AE2＋B′E2＝82＋62，
∴AB′＝10(km)．即AP＋BP＝AB′＝10km，
故出口P到A，B两村庄的最短距离和是10km.
变式：如图，在一条公路上有A、B两站相距25km，C、D为两个小镇，已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km，现在要在公路边上建设一个加油站E，使得它到两镇的距离相等，请问E站应建在距A站多远处
D
A
E
B
C
15
10
25-x
当堂练习
1.在直角三角形中，满足条件的三边长可以是 ．(写出一组即可)
【解析】答案不唯一，只要满足式子a2+b2=c2即可.
答案：3，4，5（满足题意的均可）
2.如图，王大爷准备建一个蔬菜大棚，棚宽8m，高6m，长20m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，阳光透过的最大面积是_________.
200m2
3.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解：设旗杆顶部到折断处的距离为x m，
根据勾股定理得
解得x=15, 15+9=24(m).
答：旗杆原来高24 m.
4.如图，某住宅小区在施工过程中留下了一块空地（图中的四边形ABCD），经测量，在四边形ABCD中，AB=3m，BC=4m，AD=13m，∠B=∠ACD=90°．小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问铺满这块空地共需花费多少元？
解：在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2，∴AC=5m，
在Rt△ACD中,由勾股定理,
得 CD2=AD2－AC2，∴CD=12m，
S草坪=SRt△ABC+SRt△ACD= AB BC+ AC DC
= (3×4+5×12)=36 m2．
故需要的费用为36×100=3600元．
5.如图，折叠长方形ABCD的一边AD，使点D落在BC边的F点处，若AB=8cm，BC=10cm，求EC的长.
D
A
B
C
E
F
解：在Rt△ABF中,由勾股定理,
得 BF2=AF2－AB2=102－82
BF=6(cm).
∴CF=BC－BF=4.
设EC=x ，则EF=DE=8－x ，
在Rt△ECF中,根据勾股定理,
得 x2+ 42=(8－x)2
解得 x=3.
所以EC的长为3 cm.
探索勾股定理
勾股定理的验证
课堂小结
勾股定理的简单运用