勾股定理复习题（内有详细讲解）

勾股定理复习题
(翠园初中 黄缨)
一、单选题
1.在Rt△ABC中，∠C=90°，AB=10，AC=8，则BC=( )
A. 6 B. 8 C. 10 D.
2.如图，点A坐标为（3，0），B是y轴正半轴上一点，AB=5，则点B的坐标为（ ）
A. （4，0） B. （0，4） C. （0，5） D. （0， ）
3.在△ABC中，AB=15，AC=13，BC上的高AD长为12，则△ABC的面积为（ ）
A. 84 B. 24 C. 24或84 D. 42或84
4.如图，有一块直角三角形纸片，两直角边AB＝6，BC＝8，将△ABC折叠，使AB落在斜边AC上，折痕为AD，则BD的长为( )
A. 6 B. 5 C. 4 D. 3
5.直角三角形的两条边长为5和12，它的斜边长为（ ）
A. 13 B. C. 13或 D. 13或12
6.如图，折叠长方形纸片ABCD的一边AD，使点D落在BC边上的点F处，已知AB＝8cm，BC＝10cm，则折痕AE的长为（ ）
A. cm B. cm C. 12cm D. 13 cm
7.如图，一场大风后，一棵大树在高于地面 1 米处折断，大树顶部落在距离大树底部 3 米处的地面上，那么树高是（ ）
A. 4m B. m C. （ +1）m D. （ +3）m
8.下列四组数据不能作为直角三角形的三边长的是（ ）
A. 6、8、10 B. 5、12、13 C. 12、18、22 D. 9、12、15
二、填空题
9.已知△ABC的三边长分别是6cm、8cm、10cm，则△ABC的面积是________
10.如图，正方形B的面积是________.
11.如图，正方形的面积是________cm2.
12.如图，在Rt△ABC中，∠ACB=90°，AD平分∠CAB，交CB于点D，DE⊥AB，垂足为E．若AC=3，AB=5，则DE的长为________。
三、解答题
13.在等腰△ABC中，AB=AC=10，BC=12，求BC边上的高线AD的长。
14.如图：Rt△ABC斜边BC的中垂线交AB边于点E，若AC=3，BC=5，求AE的长
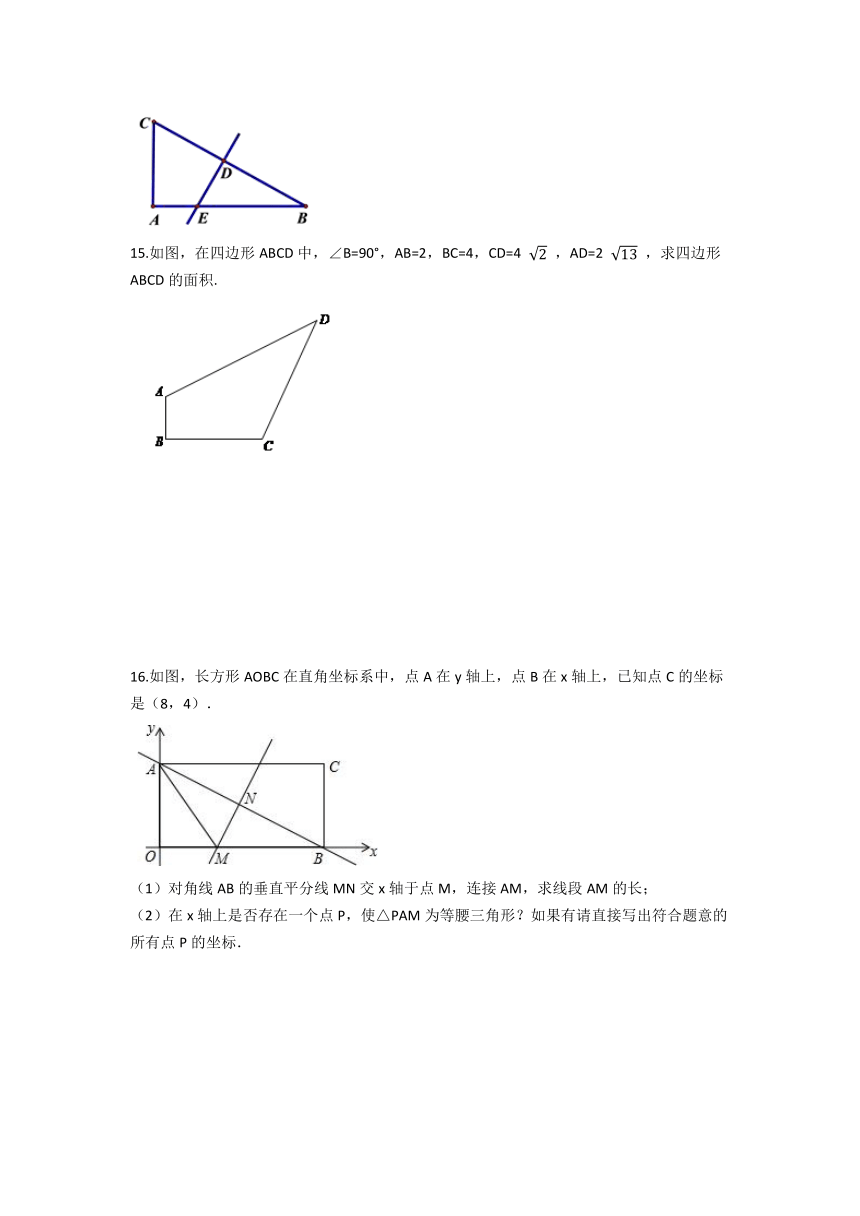
15.如图，在四边形ABCD中，∠B=90°，AB=2，BC=4，CD=4 ，AD=2 ，求四边形ABCD的面积.

16.如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．
（1）对角线AB的垂直平分线MN交x轴于点M，连接AM，求线段AM的长；
（2）在x轴上是否存在一个点P，使△PAM为等腰三角形？如果有请直接写出符合题意的所有点P的坐标．
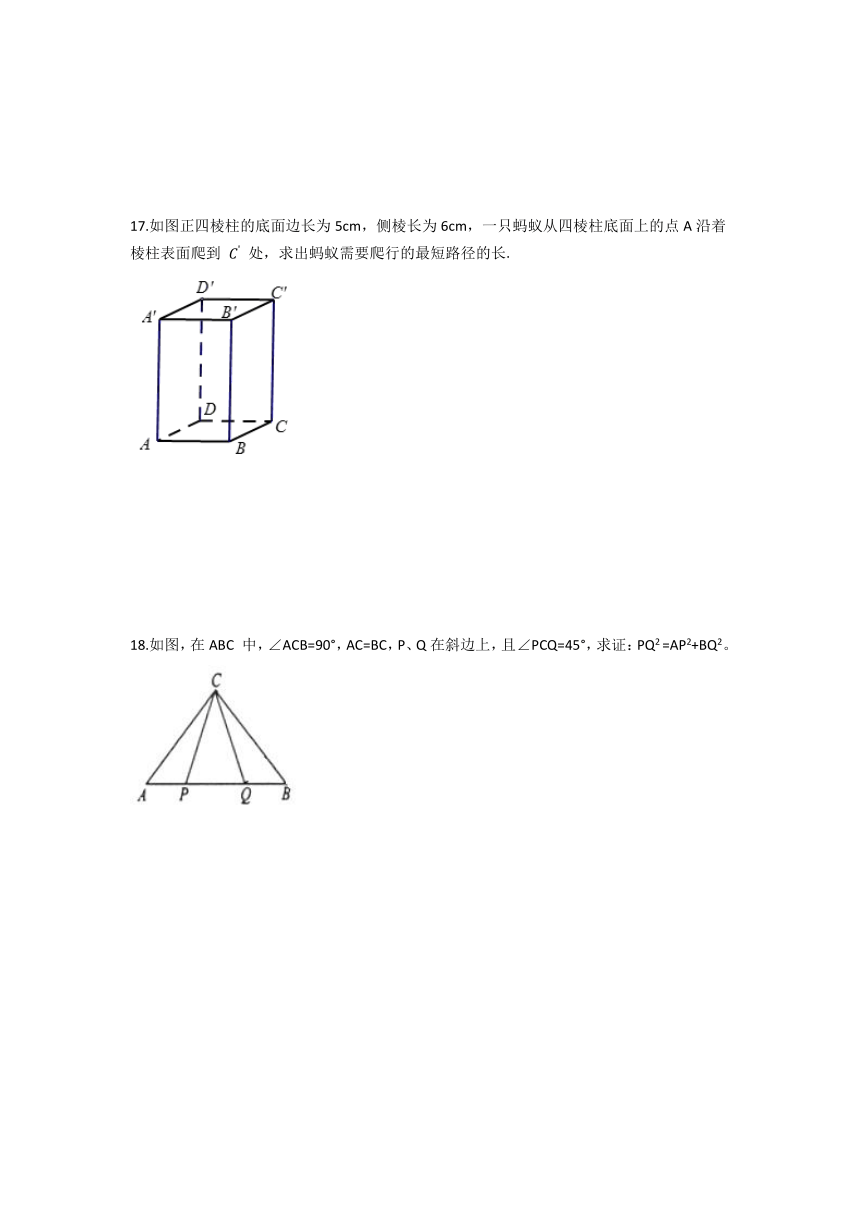
17.如图正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从四棱柱底面上的点A沿着棱柱表面爬到 处，求出蚂蚁需要爬行的最短路径的长.
18.如图，在ABC 中，∠ACB=90°，AC=BC，P、Q在斜边上，且∠PCQ=45°，求证：PQ2 =AP2+BQ2。
答案解析部分
一、单选题
1.【答案】 A
【解析】【解答】解：∵Rt△ABC中AB=10，AC=8
∴BC2=AB2-AC2
∴BC2=100-64
解之：BC=6（取正值）.
故答案为：A.
【分析】利用勾股定理直接进行计算，可求出BC的长。
2.【答案】 B
【解析】【解答】解：因为点A坐标为（3，0），B是y轴正半轴上一点，AB=5，
所以OB= =4 ，
所以点B的坐标为（0，4），
故答案为：B.
【分析】根据勾股定理算出OB的长，再根据点的坐标与图形的性质即可得出点B的坐标.
3.【答案】 C
【解析】【解答】解：（1）△ABC为锐角三角形，高AD在三角形ABC的内部，
∴BD= =9，CD= =5，
∴△ABC的面积为 =84，
（ 2 ）△ABC为钝角三角形，高AD在三角形ABC的外部，
∴BD= =9，CD= =5，
∴△ABC的面积为 =24，
故答案为：C.
【分析】当△ABC为锐角三角形，高AD在三角形ABC的内部，根据勾股定理算出BD、CD的长，从而根据BC=BD+CD算出BC的长，进而
根据三角形的面积计算公式算出答案；△ABC为钝角三角形，高AD在三角形ABC的外部，根据勾股定理算出BD、CD的长，从而根据
BC=BD-CD算出BC的长，进而根据三角形的面积计算公式算出答案.
4.【答案】 D
【解析】【解答】解：∵△ABC为直角三角形，AB=6，BC=8，
∴根据勾股定理得： ，
设BD=x，由折叠可知：ED=BD=x，AE=AB=6，
可得：CE=AC-AE=10-6=4，CD=BC-BD=8-x，
在Rt△CDB'中，
根据勾股定理得：（8-x）2=42+x2 ，
解得：x=3，
则BD=3.
故答案为：3.
【分析】首先根据勾股定理算出AC的长，设BD=x，由折叠可知：ED=BD=x，AE=AB=6，故CE=AC-AE=10-6=4，CD=BC-BD=8-x，在Rt△CDB'中，建立方程，求解即可.
5.【答案】 D
【解析】【解答】解：1）当12是直角边时，由勾股定理得：
斜边长=
2）当12是斜边时，斜边=12, 另一直角边=
故答案为：D.
【分析】因为没有明确谁是最大边，分两种情况求斜边的长，当12是直角边时，由勾股定理列式即可求得斜边长；当12是最大边，即斜边时也成立，所以有两种情况.
6.【答案】 A
【解析】【解答】解：∵△AEF由△AED翻折而成，
∴AF=AD=10cm，∠AFE=∠D=90°，DE=EF，
∴Rt△ABF中，
BF= =6cm，
∴CF=BC-BF=10-6=4cm，
设DE=x，EF=x，EC=8-x.
在Rt△ECF中，
CE2+CF2=EF2 ， 即，（8-x）2+42=x2 ，
解得x=5cm，即DE=5cm，
再在△ADE中，
AE= cm.
故答案为：A.
【分析】根据矩形的性质及折叠的性质得出AF=AD=10cm，∠AFE=∠D=90°，DE=EF，Rt△ABF中，利用勾股定理算出BF的长，设DE=x，EF=x，EC=8-x，在Rt△ECF中，利用勾股定理建立方程，求解算出DE的长，最后再根据勾股定理算出AE的长即可.
7.【答案】 C
【解析】【解答】解：根据勾股定理可知：折断的树高= = 米，
则这棵大树折断前的树高=（1+ ）米.
故答案为：C.
【分析】首先根据勾股定理算出折断的树高，再用折断的树高加上1即可得出折断前大树的高度.
8.【答案】 C
【解析】【解答】解：A. ∵ ，∴此三角形为直角三角形，故错误，不符而合题意；
B. ∵ ，∴此三角形为直角三角形，故错误，不符而合题意；
C. ∵ ，∴此三角形不是直角三角形，故正确，不符而合题意；
D. ∵ ，∴此三角形为直角三角形，故错误，不符而合题意.
故答案为：C.
【分析】根据勾股定理的逆定理，一个三角形的三边如果满足较小两边的平方和等于最大边长的平方，那么这个三角形是直角三角形，从而即可一一判断得出结论.
二、填空题
9.【答案】 24cm2
【解析】【解答】解：∵62+82=102 ，
∴△ABC是直角三角形.
∴△ABC的面积为： ×6×8=24.
故答案为：24cm2.
【分析】首先根据勾股定理的逆定理判断出△ABC是直角三角形，进而根据直角三角形的面积计算方法即可算出答案.
10.【答案】 144.
【解析】【解答】解：如图，根据勾股定理可以得出：
a2+b2=c2 ，
a2=25，c2=169，
b2=169-25=144，
因此B的面积是144.
故答案为：144.
【分析】根据勾股定理可以得出a2+b2=c2 ， 故b2=c2-a2=144=正方形B的面积.
11.【答案】 25
【解析】【解答】由题意得，正方形的面积是132-122=25cm2.
【分析】由题意用勾股定理可求得正方形的边长，然后根据正方形的面积=边长2即可求解.
12.【答案】
【解析】【解答】解：∵Rt△ABC中，
,
∵AD平分∠CAB，DE⊥AB，∠ACB=90°即AC⊥CB
∴CD=DE，
在Rt△ACD和Rt△AED中，
∴Rt△ACD≌Rt△AED（HL）
∴AC=AE=3
∴BE=AB-AE=5-3=2，
设DE=CD=x，则BD=4-x
在Rt△BDE中
BD2=DE2+BE2
∴（4-x）2=x2+4
解之：
∴
故答案为：.
【分析】利用勾股定理求出BC的长，再利用角平分线的性质，易证CD=ED，利用HL证明Rt△ACD≌Rt△AED，根据全等三角形的对应边相等，可证得AC=AE，即可求出BE的长，然后在Rt△BDE中，利用勾股定理求出DE的长。
三、解答题
13.【答案】 解：∵∠AB=AC,AD是高线,∴BD=CD=6,
在△ABC中,AD= =8
【解析】【分析】根据等腰三角形的三线合一的性质，可求出BD的长，再利用勾股定理求出AD的长。
14.【答案】 解：连接CE，
设AE=x.
∵在Rt△ABC中，AC=3，BC=5，
∴AB= .
∵DE是BC的中垂线，
∴BE=CE=4-x，
∵AC2+AE2=CE2 ，
∴32+x2=(4-x)2 ，
∴x= ，即
【解析】【分析】连接CE，设AE=x.由勾股定理可求出AB=4，由线段中垂线的性质可知CE=BE=4-x，根据AC2+AE2=CE2列方程求解即可.
15.【答案】 解：连接AC，如图所示：

∵∠B=90°，AB=2，BC=4，
∴AC= ，
∵CD=4 ，AD=2 ，
∴(2 )2+(4 )2＝(2 )2 ，
∴AC2+CD2=AD2.，
∴△ACD是直角三角形，
∴四边形ABCD的面积=△ABC的面积+△ACD的面积= ×2×4+ ×2 ×4 ＝4+4
【解析】【分析】 连接AC，如图所示： 首先根据勾股定理算出AC的长，再根据勾股定理判断出 △ACD是直角三角形， 且∠ACD是直角，然后根据四边形ABCD的面积=△ABC的面积+△ACD的面积即可算出答案.
16.【答案】 （1）解：由题意得：OA=4，OB=8，
∵MN是AB的垂直平分线，
∴AM=BM，
设AM=x，则BM=x，OM=8-x，
Rt△AOM中，由勾股定理得：AO2+OM2=AM2 ，
∴42+（8-x）2=x2 ，
解得：x=5，
∴AM=5.
（2）解：如图，①当AP1=AM=5时，OM=OP1=3，此时P1（-3，0）；
②当AM=P2M=P3M=5时，此时P2（-2，0），P3（8，0）；
③如图，作AM的垂直平分线，交AM于E，交x轴于P4 ，
∴EM= ，
∴P4M= ，
∴OP4= -3= ，此时P4（- ，0），
综上，△PAM为等腰三角形，点P的坐标是（-3，0）或（-2，0）或（8，0）或（- ，0）．
【解析】【分析】（1）由点C的坐标可得矩形AOBC的长和宽，又根据线段垂直平分线的性质可知AM=BM，在Rt△AOM中，由OA=4、AM+OM=8，借助勾股定理建立AM的方程即可求解；
（2）分AM作底和作腰两种情况考虑：当AM作腰且A为顶角顶点，此时有AM=AP1；当AM作腰且M为顶角顶点，此时有MA=MP2=MP3 ， 利用等腰三角形三线合一和两腰相等的性质，即可分别求出P1、P2、P3的坐标；当AM作底，此时有P4M=P4A，P4E垂直平分AM，进而解Rt△EP4M可得P4M的长，从而确定P4的坐标，据此即可解答。
17.【答案】解：当沿着平面ABB'A'、平面A'B'C'D'爬行时，
cm
当沿着平面 、平面 爬行时，
cm
因为 ＜ ，
所以蚂蚁需要爬行的最短路径的长是 cm.
【解析】【分析】根据两点之间直线最短，可利用勾股定理求出最短路径。
18.【答案】证明：如图，在PC的右侧作CP的垂线，并截取CD=CP，连接BD，QD，则∠DCQ=∠PCQ=45°，于是可证△DCB≌△PCA（SAS），得AP=BD，∠DBC=∠A=45°，∴∠DBQ=90°，再证△DCQ≌△PCQ（SAS），得DQ=PQ，Rt△DBQ中，DQ =BQ +BD 即PQ2 =AP2+BQ2。
【解析】【分析】如图，在PC的右侧作CP的垂线，并截取CD=CP，连接BD，QD，∠DCQ=∠PCQ=45°，于是利用SAS可证△DCB≌△PCA，根据全等三角形的性质得出AP=BD，∠DBC=∠A=45°，再利用SAS判断出△DCQ≌△PCQ，根据全等三角形对应边相等得出DQ=PQ，Rt△DBQ中，利用勾股定理得出DQ =BQ +BD ，再等量代换即可得出答案。