五环导学案:北师大数学八年级上册第一章(PDF版,无答案)
文档属性
| 名称 | 五环导学案:北师大数学八年级上册第一章(PDF版,无答案) |
|
|
| 格式 | |||
| 文件大小 | 987.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 14:18:48 | ||
图片预览




文档简介
1.1 探索勾股定理(一)
一、激活思维
(1)在直角三角形中,任意两条边确定了,另外一条边也会随之确定吗?为
什么?
(2)三边之间存在着一种特定的数量关系吗?为什么?
二、探究新知
问题 1:下面图形以等腰直角三角形的三边作为边长,分别向外作出三个正方形
A、B、C,请你观察、思考、计算并填空:
①图 1-1 中,正方形 A的面积是____个单位面积;正方形 B的面积是____个单位
面积;正方形 C的面积是____个单位面积;
②图 1-2 中,正方形 A的面积是____个单位面积;正方形 B的面积是____个单位
面积;正方形 C的面积是____个单位面积;
你能发现 A、B、C三个正方形的面积之间有什么样的关系吗?
问题 2:在下面的方格纸上,任意画出一个顶点都在格点上的直角三角形,并分
别以这个直角三角形的各边为一边向三角形外部作正方形,你所画的 3个正方形
面积之间有怎样的数量关系?
问题 3:如右图,如果 Rt△ABC 中两直角边分别记为 a、b, 斜边为 c,我们可以
把问题 1和 2的结论表示为: 。
� �
A
c
b cb
C a B
a
小结:直角三角形两直角边的平方和等于斜边的平方。这就是著名的勾股定理,
其中:条件是______________,结论是_______________.我国古代把直角三角形
较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。
三、双基巩固
例 1:如图,在下列横线上填上适当的值:
x= , y= , n=
四、综合运用
例 2:如图,在△ABC 中,∠BAC=90°,AB=6,AC=8,AD⊥BC,垂足为 D,求
BC,AD 的长.
五、分层反馈
�� �1.求下图中字母所代表的正方形的面积。
81
A
225 B
225
400
A=__________ B=____________
2.已知:如图,在△ABC 中,AB=13,AC=20,AD=12,且 AD⊥BC,垂足为点
D,求 BC 的长.
3.如图,求等腰三角形 ABC 的面积.
4.(★)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中
最大的正方形的边长是 8cm,则图中的所有的正方形的面积之和是 .
1.1 探索勾股定理(二)
一、激活思维
勾股定理
� 图形 定理条件 定理结论 直接应用
在 Rt △ ABC 中 ,
A
a=40,b=9,
c
b
则c2 =
C a B
二、探究新知
问题探究:如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是 a,
b,斜边长为 c)和一个边长为 c的正方形,请你将它们拼成一个能证明勾股定
理的图形,并利用此图形证明勾股定理.
方法 1:利用 4个全等的直角三角形拼出了右图的大正方形。
证明:从整体看,大正方形面积可以表示为: ,
如果分为五个部分来看,
又可以表示为:
+ + + + c2
则: =
因此:
方法 2:利用同样的 4个全等的直角三角形拼出了右图的正方形。
证明:从整体看,大正方形面积可以表示为: ,
如果分为五个部分来看,
又可以表示为:
+ + + + (b-a)2
则: =
因此:
三、双基巩固
例 1:如图,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方 4000
米处,过了 20 秒,飞机距离这个男孩头顶 5000 米。飞机每秒飞行多少米?
四、综合运用
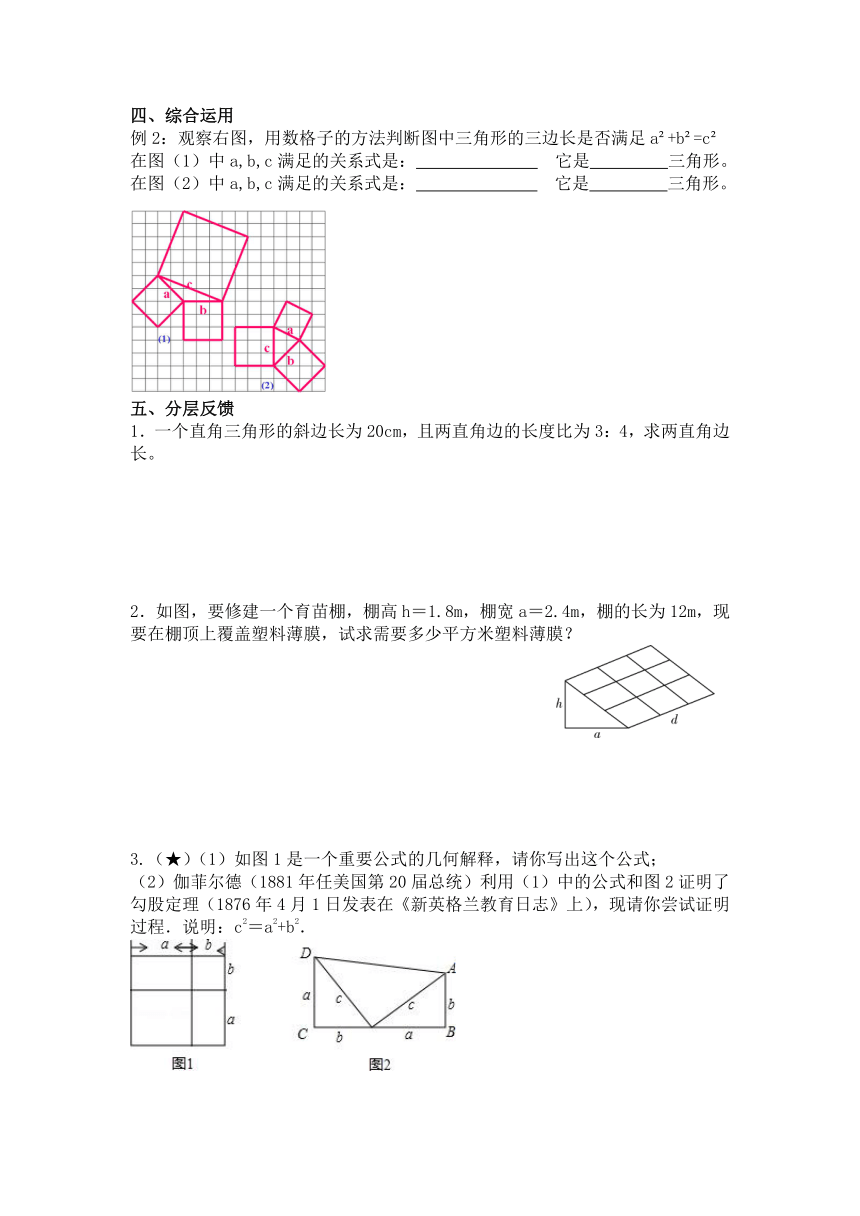
例 2:观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c
在图(1)中 a,b,c 满足的关系式是: 它是 三角形。
在图(2)中 a,b,c 满足的关系式是: 它是 三角形。
五、分层反馈
1.一个直角三角形的斜边长为 20cm,且两直角边的长度比为 3:4,求两直角边
长。
2.如图,要修建一个育苗棚,棚高 h=1.8m,棚宽 a=2.4m,棚的长为 12m,现
要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
3.(★)(1)如图 1是一个重要公式的几何解释,请你写出这个公式;
(2)伽菲尔德(1881 年任美国第 20 届总统)利用(1)中的公式和图 2证明了
勾股定理(1876 年 4 月 1 日发表在《新英格兰教育日志》上),现请你尝试证明
2 2 2
过程.说明:c=a +b .
1.2 一定是直角三角形吗
一、探究新知
问题 1(猜想)在一个直角三角形中,两直角边的平方和等于斜边的平方。反过
来,如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是直
角三角形吗?
问题 2(检验)下面的每组数是一个三角形的三边 a,b,c ,而且满足 a2 b2 c2 :
3,4,5;5,12,13;8,15,17.分别以每组为三边长画出三角形,它们是直角三角形
吗?
问题 3(归纳)如果三角形的三边长 a,b,c 满足 ,那么这个三角形
是 三角形。
2 2 2
定义:满足 a +b =c 的三个 ,称为勾股数。常用的勾股数有:(3、
4、5);(6、8、10);(9、12、15);(5、12、13);(8、15、17);(7、24、25);
(9、40、41)。
问题 4(证明,选做)你能证明这个结论吗?
二、双基巩固
例 1:一个零件的形状如左下图所示,按规定这个零件中∠A和∠DBC 都应为直
角,工人师傅量的这个零件各边尺寸如右下图所示,这个零件符合要求吗?
例 2:如图,在正方形 ABCD 中,AB=4,AE=2,DF=1,试说明 BEF 的形状,并说
明你的判断理由。
三、综合运用
例 3:四边形 ABCD 中已知 AB=3, BC=4, CD=12, DA=13,且∠ABC=90°,求这个
四边形的面积。
四、分层反馈
1已知 a、b、c分别是△ABC 的三边,下列条件:①a=12,b=5,c=13;②a:
b:c=1:3:4;③a=8,b=15,c=17;④a=12,b=11,c=5.其中能判
断△ABC 为直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
2.将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是( )
A. 是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
3.如图,在长方形 ABCD 中,AB=CD=24,AD=BC=50,E 是 AD 上一点,且 AE:
DE=9:16,判断△BEC 的形状,并说明理由.
4.(★)阅读并回答问题:能够成为直角三角形三条边长的三个正整数 a,b,c,
称为勾股数,在一次数学活动课上,王老师设计了如下数表:
n 2 3 4 5 …
a 22﹣1 8 15 24
b 4 6 8 10
2
c 2 +1 10 17 26
(1)请你分别现察 a,b,c 与 n 之间的关系,并用含自然数 n(n>1)的代数
式表示:a= ,b= ,c= .
(2)猜想:以 a,b,c为边的三角形是否为直角三角形?并证明你的猜想.
(3)观察下列勾股数 32+42=52,52+122=132,72+242=252,92+402=412,分析其
中的规律,写出第五组勾股数
习题课 1:股定理及逆定理的基本运算
一、知识方法
(1)勾股定理:如果直角三角形的两条直角边长分别是 a,b,斜边长为 c,那
么________.
(2)若 Rt△ABC 的两条直角边长分别是 a,b,斜边长为 c,则SRt△ABC=________.
(3)勾股逆定理:若三角形的三边分别是 a,b,c,且满足a2+b2= c2,则三角
形是以____为斜边的____________三角形.
二、典例精讲
【例 1】利用勾股定理求边长
(1)已知:如 A 图,在△ABC 中,AB=13,AC=20,BC=21,AD⊥BC,垂足为
点 D.(1)求 AD 的长;(2)求 BD、CD 的长;(3)求△ABC 的面积.
(2)如图,四边形 ABCD 中,AB=3,BC=4,CD=12,AD=13,且∠B=90°,求四边
形 ABCD 的面积.
(3)如图所示的一块草地,已知 AD=4m,CD=3m,AB=12m,BC=13m,且∠CDA=90°,
求这块草地的面积。
【例 2】勾股定理逆定理的应用
(1)(龙岗)下列条件中,不能判断△ABC 是直角三角形的是( )
A.a:b:c=3:4:5 B.∠A:∠B:∠C=3:4:5
C.∠A+∠B=∠C D.a 2 : b 2 : c 2 3 : 4 : 5
(2)如图,每个小正方形的边长都为 1,△ABC 的顶点都在格点上.
(1)判断△ABC 是什么形状,并说明理由.(2)求△ABC 的面积.
三、进阶训练
1.下面能够成直角三角形三边长的是( )
A.5,6,7 B.5,12,13 C.1,4,9 D.5,11,12
2.分别满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为 1︰2︰3 B.三边长的平方之比为 1︰2︰3
C.三边长之比为 3︰4︰5 D.三内角之比为 3︰4︰5
3.已知三角形三边长为 a、b、c,如果(a 5)2 + b 12 + c2-26c+169=0,则△
ABC 是( )
A.以 a 为斜边的直角三角形 B.以 b 为斜边的直角三角形
C.以 c 为斜边的直角三角形 D.不是直角三角形
4.若在一直角三角形中一直角边与斜边分别为 12、13,则面积为_____,斜边上
的高为______.
5.在△ABC 中,BC=10,AB=13,中线 AD=12,则 AC=________.
6.(龙岗)在 Rt△ABC 中,∠C=90°,AC=9,BC=12,则点 C到 AB 的距离是 7.
在△ABC 中,∠C=90°,两直角边长之比为 3:4,斜边长为 25,则这个三角形的
面积是________.
7.如图,小方格都是边长为 1的正方形,求四边形 ABCD 的面积________.
D
A
C
B
第 7 题图 第 8题图 第 9 题图
8.如图,在四边形 ABCD 中,∠B=∠D=90°,AB=BC=2,CD=1,求 AD 的长.
9.(罗湖)如图,有一块直角三角形纸片,两直角边 AC=6cm,BC=8cm,现将直
角边 AC 沿着直线 AD 折叠,使它落在斜边 AB 上,且与 AE 重合,则 CD 的长为
_______cm.
10.如图,在正方形网格中,每个小正方形的边长均为 1,点 A、B、C、D 均在
格点上.
(1)图中线段 BC 的长度平方为 ;
(2)求图中格点四边形 ABCD 的面积.
11.如图,正方形网格的每个小方格都是边长为 1的正方形,△ABC 的顶点都在
格点上.(1)试判断△ABC 是什么三角形,并说明理由.(2)求△ABC 的面积.
1.3 勾股定理的应用(1)
�
一、激活思维
A
c
b
C a B
定理条件 定理结论 应用
勾股定理
勾股定理逆定理
二.探究新知
探究 1:如右图:有一个圆柱,它的高等于 12 厘米,底面半径等于 3厘米,
在圆柱下底面上的 A点有一只蚂蚁,它想从点 A爬到点 B , 蚂蚁沿着圆柱
侧面爬行的最短路程是多少 (π的值取 3)
(1)想一想,尝试从 A到 B沿圆柱的侧面画出几条路线,你觉得
从 A点到 B点哪条路线最短? B
A
(2)如图,将圆柱侧面剪开展成一个长方形,从 A点到 B点最短路线是什么?
B B
A
A
(3)蚂蚁从 A点出发,想吃到 B 点上的食物,他沿圆柱侧面爬行的最短路程是
多少?
�
A
c
b
C a B
������
A
c
b
C a B
探究 2:如图,长方体的长为 3cm,宽为 2cm,高为 4cm,点 B到点 C的距离为
1cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点 B,需要爬行的最短距离
是?
三、分层反馈
1.一个底面周长为 10cm,高为 12cm 的圆柱,有一只小虫从底部点 A 处爬到上
底 B 处,则小虫所爬的最短路径长是 cm.
2.如图 1,有一圆柱,它的高等于 8cm,底面直径等于 4cm(π=3),在圆柱下
底面的 A 点有一只蚂蚁,它想吃到上底面与 A 相对的 B 点处的食物,需要爬
行的最短路程大约( )
A.10cm B.12cm C.19cm D.20cm
3.如图,正方体的棱长为 2,B为一条棱的中点.已知蚂蚁沿正方体的表面从 A
点出发,到达 B点,则它运动的最短路程为
4.(★)如图,长方体的高为 3cm,底面是正方形且边长为 2cm,现有一只蚂蚁
从 A点出发,沿长方体表面到达 C点,求蚂蚁行走的最短路线.
1.3 勾股定理与逆定理的应用(2)
�
一、激活思维
A
c
b
C a B
定理条件 定理结论 应用
勾股定理
勾股定理逆定理
二.探究新知
探究 1:如图,李叔叔想要检测雕塑底座正面的 AD 和 BC 是否分别垂直于底边
但他随身只带了有刻度的卷尺,李叔叔量得 AD 长 30 厘米,AB 长 40 厘米,BD
长 50 厘米,则 AD 边垂直于 AB 边吗?
探究 2:如图,滑杆在机械槽内运动,∠ACB 为直角,已知滑杆 AB 长 2.5 米,顶
端 A在 AC 上运动,量得滑杆下端 B距 C点的距离为 1.5 米,当端点 B向右移动
0.5 米时,求滑杆顶端 A下滑多少米?
探究 3:如图,甲、乙两船同时从 A 港口出发,甲船以每小时 30 海里的速度向
西偏北 32°的方向航行 2小时到达 C岛,乙船以每小时 40 海里的速度航行 2
小时到 B岛,已知 B、C两岛相距 100 海里,求乙船航行的方向.
三.分层反馈
�
A
c
b
C a B
������
A
c
b
C a B
1.如图 2,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测
量了下,发现 AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检
验一下挖的是否合格?
2.有一个水池,水面是一个边长为 10 尺的正方形,在水池正中央有一根新生的芦
苇,它高出水面 1 尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,
请问这个水池的深度和这根芦苇的长度各是多少
3.如图是一个三级台阶,它的每一级的长、宽、高分别为 20dm、3dm、2dm.A
和 B 是这个台阶上两个相对的端点,点 A 处有一只蚂蚁,想到点 B 处去吃可
口的食物,则蚂蚁沿着台阶面爬行到点 B的最短路程为?
4.(★)如图,将长方形 ABCD 边 AD 沿折痕 AE 折叠,使点 D 落在 BC 上的点 F
处,已知 AB=6,△ABF 的面积是 24,求 DE 的长.
5.如图,有一艘货船和一艘客船同时从港口 A 出发,客船每小时比货船多走 5
海里,客船与货船速度的比为 4:3,货船沿东偏南 10°方向航行,2小时后
货船到达 B处,客船到达 C处,若此时两船相距 50 海里.(1)求两船的速度
分别是多少?(2)求客船航行的方向.
习题课:勾股定理与折叠综合运用
一、知识方法
(1)勾股定理:如果直角三角形的两条直角边长分别是 a,b,斜边长为 c,那
么 .
(2)折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的 和
不变,位置变化, 和 相等.
二、典例精讲
例 1:(三角形)如图,点 D 在△ABC 的边 AC 上,将△ABC 沿 BD 翻折后,点 A恰
好与点 C重合,若 BC=5,CD=3,则 BD 的长
例 2:(长方形)如图,在长房形纸片 ABCD 中,AB=12,BC=5,点 E在 AB 上,
将△DAE 沿 DE 折叠,使点 A落在对角线 BD 上的点 A′处,则 AE 的长
例 3:(正方形)如图,将边长为 8cm 正方形纸片 ABCD 折叠,使点 D 落在 BC 边
的中点 E处,点 A落在点 F处,折痕为 MN,则线段 CN 的长
三、进阶训练
1.如图,在△ABC 中,∠C=90°,将△ACE 沿着 AE 折叠以后 C 点正好落在 AB
边上的点 D处.
(1)当∠B=28°时,求∠AEC 的度数;
(2)当 AC=6,AB=10 时,①求线段 BC 的长;②求线段 DE 的长.
2.如图,在长方形 ABCD 中,AB=3,BC=5,在 CD 上任取一点 E,连接 BE,将
△BCE 沿 BE 折叠,使点 C恰好落在 AD 边上的点 F处,则 CE 的长为( )
A.2 B. C.1 D.
3.如图,将边长为 8cm 的正方形纸片 ABCD 折叠,使点 D落在 AB 边中点 E处,点
C落在点 Q处,折痕为 FH,则线段 AF 的长是( )
A.3cm B.4cm C.5cm D.6cm
4.如图,长方形 ABCD 中,AB=4,BC=3,将其沿直线 MN 折叠,使点 C 与点 A
重合,则 CN 的长
5.如图,长方形 ABCD 中,点 E 在边 AB 上,将矩形 ABCD 沿直线 DE 折叠,点 A
恰好落在边 BC 的点 F处.若 AE=10,BF=6,则 CD 的长
单元复习课 1:勾股定理及其应用
一、问题导思
问题 1:直角三角形的边、角之间分别存在着什么关系
问题 2:举例说明:如何判断一个三角形是否为直角三角形?
问题 3:举例说明:运用勾股定理可以解决那些问题?
问题 4:搜集并列举勾股定理的有关历史。
二、知识建构
问题 5:梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现
全章知识结构。
三、考点精讲
考点 1:勾股定理与面积
例 1:如图,方格纸上每个小正方形的面积为 1个单位.
(1)在方格纸上,以线段 AB 为边画正方形并计算所画正方形的面积,解释
你的计算方法.
(2)你能在图上画出面积依次为 5 个单位、10 个单位、13 个单位的正方形
吗?
考点 2:勾股定理的计算
例 2:如图 BC 长为 3cm,AB 长为 4cm,AF 长为 12cm,正方形 CDEF 的面积=
例 3:如图,在一只底面半径为 3cm,高为 8cm 的圆柱体状水杯中放入一支 13cm
长的吸管,这支吸管露出杯口的长度=
考点 3:判断直角三角形
例 4:相传,古埃及人用 13 个等距的结把一根绳子分成等长的 12 段.并把它摆
成△ABC 的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直
角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,
并说明理由.
例 5:五根小木棒,其长度分别为 7,15,20,24,25,现将它们摆成两个直角
三角形,如图,其中正确的是( )
A B C D
考点 4:勾股定理的应用
40
例 6:如图,一个底面直径为 cm,高为 30cm 的糖罐子,一只蚂蚁从 A处沿着
糖罐的表面爬行到 B处,则蚂蚁爬行的最短距离是
例 7:如图是一个滑梯示意图,若将滑梯 AC 水平放置,则刚好与 AB 一样长.已
知滑梯的高度 CE=3m,CD=1m,求滑道 AC 的长= .
四、易错突破
易错 1: C 不一定是直角
例:在Rt ABC 中,若 AC=3,BC=4,则AB 2 .
易错 2:三角形不一定是直角三角形
例:在 ABC 中, A, B, C 所对的边分别是a,b,c ,且a 3,b 4,若三边长
为连续整数,则 c= .
易错 3:忽略展开图的多种情况
例:如图,长方体的长为 15,宽为 10,高为 20,点 B离点 C的距离是 5,一只
蚂蚁如果要沿着长方体的表面从点 A爬到点 B,需要爬行的最短距离是多少?
易错 4:忽略多图情况
例:(★)在△ABC 中,AB=15,AC=20,BC 边上的高 AD=12,试求 BC 的长.
五、达标测试(时间 25 分钟,满分 50 分;客观题每题 3 分,分数: )
1.如果直角三角形的两直角边长是 9,12,那么斜边长为( )
A.15 B.13 C.17 D.19
2.满足下列条件的△ABC,不是直角三角形的是( )
2 2 2
A.b =c ﹣a B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=12:13:15
3.下面说法正确的是( )
2 2 2
A.在 Rt△ABC 中,a +b =c
B.在 Rt△ABC 中,a=3,b=4,那么 c=5
C.直角三角形两直角边都是 5,那么斜边长为 10
D.直角三角形中,斜边最长
4.如果把直角三角形的两条直角边同时扩大到原来的 2 倍,那么斜边扩大到原
来的( )
A.1倍 B.2倍 C.3倍 D.4倍
5.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据不符合
直角三角形的三边长的是( )
A.3,4,5 B.6,8,10 C.5,12,13 D.13,16,18
6.如图,将一根长为 8cm(AB=8cm)的橡皮筋水平放置在桌面上,固定两端 A
和 B,然后把中点 C 竖直地向上拉升 3cm 至 D 点,则拉长后橡皮筋的长度为
( )
A.8cm B.10cm C.12cm D.15cm
7.如图是某地的长方形广场的示意图,如果小明要从 A 角走到 C角,那么至少
要走( )
A.90m B.100m C.120m D.140m
8.如图,一圆柱高 5cm,底面半径 4cm,一只蚂蚁从点 A爬到点 B处吃食,要爬
行的最短路程(π取 3)是( )
A.13cm B.26cm C.17cm D.9cm
9.在 Rt△ABC 中,∠B=90°,a=3cm,b=4cm,则第三边的平方是 .
10.如图,在△ABC 中,∠ACB=90°,BC=6,AC=8,CD⊥AB,垂足为 D.则
CD 的长为 .
11.(4 分)已知在 Rt△ABC 中,∠C=90°,AB=10,BC=8,求 AC 的长.
12.(4 分)如图,在 Rt△ABC 中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足
为 D,求 AB 和 CD.
13.(6 分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了
避免走散,他们用两部对话机联系,已知对话机的有效距离为 15 千米,早晨
8:00 甲先出发,他以 6 千米/时的速度向东行走,1 小时后乙出发,他以 5
千米/时的速度向北行进,上午 10:00,甲、乙二人相距多远?还能保持联系
吗?
14.(6 分)观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…,
a,b,c
根据你发现的规律,请写出
(1)当 a=19 时,求 b、c的值;
(2)当 a=2n+1 时,求 b、c的值;
(3)用(2)的结论判断 15,111,112 是否为一组勾股数,并说明理由.
单元错题笔记
题号 错题与错解 错因与正解
题号 错题与错解 错因与正解
一、激活思维
(1)在直角三角形中,任意两条边确定了,另外一条边也会随之确定吗?为
什么?
(2)三边之间存在着一种特定的数量关系吗?为什么?
二、探究新知
问题 1:下面图形以等腰直角三角形的三边作为边长,分别向外作出三个正方形
A、B、C,请你观察、思考、计算并填空:
①图 1-1 中,正方形 A的面积是____个单位面积;正方形 B的面积是____个单位
面积;正方形 C的面积是____个单位面积;
②图 1-2 中,正方形 A的面积是____个单位面积;正方形 B的面积是____个单位
面积;正方形 C的面积是____个单位面积;
你能发现 A、B、C三个正方形的面积之间有什么样的关系吗?
问题 2:在下面的方格纸上,任意画出一个顶点都在格点上的直角三角形,并分
别以这个直角三角形的各边为一边向三角形外部作正方形,你所画的 3个正方形
面积之间有怎样的数量关系?
问题 3:如右图,如果 Rt△ABC 中两直角边分别记为 a、b, 斜边为 c,我们可以
把问题 1和 2的结论表示为: 。
� �
A
c
b cb
C a B
a
小结:直角三角形两直角边的平方和等于斜边的平方。这就是著名的勾股定理,
其中:条件是______________,结论是_______________.我国古代把直角三角形
较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。
三、双基巩固
例 1:如图,在下列横线上填上适当的值:
x= , y= , n=
四、综合运用
例 2:如图,在△ABC 中,∠BAC=90°,AB=6,AC=8,AD⊥BC,垂足为 D,求
BC,AD 的长.
五、分层反馈
�� �1.求下图中字母所代表的正方形的面积。
81
A
225 B
225
400
A=__________ B=____________
2.已知:如图,在△ABC 中,AB=13,AC=20,AD=12,且 AD⊥BC,垂足为点
D,求 BC 的长.
3.如图,求等腰三角形 ABC 的面积.
4.(★)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中
最大的正方形的边长是 8cm,则图中的所有的正方形的面积之和是 .
1.1 探索勾股定理(二)
一、激活思维
勾股定理
� 图形 定理条件 定理结论 直接应用
在 Rt △ ABC 中 ,
A
a=40,b=9,
c
b
则c2 =
C a B
二、探究新知
问题探究:如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是 a,
b,斜边长为 c)和一个边长为 c的正方形,请你将它们拼成一个能证明勾股定
理的图形,并利用此图形证明勾股定理.
方法 1:利用 4个全等的直角三角形拼出了右图的大正方形。
证明:从整体看,大正方形面积可以表示为: ,
如果分为五个部分来看,
又可以表示为:
+ + + + c2
则: =
因此:
方法 2:利用同样的 4个全等的直角三角形拼出了右图的正方形。
证明:从整体看,大正方形面积可以表示为: ,
如果分为五个部分来看,
又可以表示为:
+ + + + (b-a)2
则: =
因此:
三、双基巩固
例 1:如图,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方 4000
米处,过了 20 秒,飞机距离这个男孩头顶 5000 米。飞机每秒飞行多少米?
四、综合运用
例 2:观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c
在图(1)中 a,b,c 满足的关系式是: 它是 三角形。
在图(2)中 a,b,c 满足的关系式是: 它是 三角形。
五、分层反馈
1.一个直角三角形的斜边长为 20cm,且两直角边的长度比为 3:4,求两直角边
长。
2.如图,要修建一个育苗棚,棚高 h=1.8m,棚宽 a=2.4m,棚的长为 12m,现
要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
3.(★)(1)如图 1是一个重要公式的几何解释,请你写出这个公式;
(2)伽菲尔德(1881 年任美国第 20 届总统)利用(1)中的公式和图 2证明了
勾股定理(1876 年 4 月 1 日发表在《新英格兰教育日志》上),现请你尝试证明
2 2 2
过程.说明:c=a +b .
1.2 一定是直角三角形吗
一、探究新知
问题 1(猜想)在一个直角三角形中,两直角边的平方和等于斜边的平方。反过
来,如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是直
角三角形吗?
问题 2(检验)下面的每组数是一个三角形的三边 a,b,c ,而且满足 a2 b2 c2 :
3,4,5;5,12,13;8,15,17.分别以每组为三边长画出三角形,它们是直角三角形
吗?
问题 3(归纳)如果三角形的三边长 a,b,c 满足 ,那么这个三角形
是 三角形。
2 2 2
定义:满足 a +b =c 的三个 ,称为勾股数。常用的勾股数有:(3、
4、5);(6、8、10);(9、12、15);(5、12、13);(8、15、17);(7、24、25);
(9、40、41)。
问题 4(证明,选做)你能证明这个结论吗?
二、双基巩固
例 1:一个零件的形状如左下图所示,按规定这个零件中∠A和∠DBC 都应为直
角,工人师傅量的这个零件各边尺寸如右下图所示,这个零件符合要求吗?
例 2:如图,在正方形 ABCD 中,AB=4,AE=2,DF=1,试说明 BEF 的形状,并说
明你的判断理由。
三、综合运用
例 3:四边形 ABCD 中已知 AB=3, BC=4, CD=12, DA=13,且∠ABC=90°,求这个
四边形的面积。
四、分层反馈
1已知 a、b、c分别是△ABC 的三边,下列条件:①a=12,b=5,c=13;②a:
b:c=1:3:4;③a=8,b=15,c=17;④a=12,b=11,c=5.其中能判
断△ABC 为直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
2.将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是( )
A. 是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.
3.如图,在长方形 ABCD 中,AB=CD=24,AD=BC=50,E 是 AD 上一点,且 AE:
DE=9:16,判断△BEC 的形状,并说明理由.
4.(★)阅读并回答问题:能够成为直角三角形三条边长的三个正整数 a,b,c,
称为勾股数,在一次数学活动课上,王老师设计了如下数表:
n 2 3 4 5 …
a 22﹣1 8 15 24
b 4 6 8 10
2
c 2 +1 10 17 26
(1)请你分别现察 a,b,c 与 n 之间的关系,并用含自然数 n(n>1)的代数
式表示:a= ,b= ,c= .
(2)猜想:以 a,b,c为边的三角形是否为直角三角形?并证明你的猜想.
(3)观察下列勾股数 32+42=52,52+122=132,72+242=252,92+402=412,分析其
中的规律,写出第五组勾股数
习题课 1:股定理及逆定理的基本运算
一、知识方法
(1)勾股定理:如果直角三角形的两条直角边长分别是 a,b,斜边长为 c,那
么________.
(2)若 Rt△ABC 的两条直角边长分别是 a,b,斜边长为 c,则SRt△ABC=________.
(3)勾股逆定理:若三角形的三边分别是 a,b,c,且满足a2+b2= c2,则三角
形是以____为斜边的____________三角形.
二、典例精讲
【例 1】利用勾股定理求边长
(1)已知:如 A 图,在△ABC 中,AB=13,AC=20,BC=21,AD⊥BC,垂足为
点 D.(1)求 AD 的长;(2)求 BD、CD 的长;(3)求△ABC 的面积.
(2)如图,四边形 ABCD 中,AB=3,BC=4,CD=12,AD=13,且∠B=90°,求四边
形 ABCD 的面积.
(3)如图所示的一块草地,已知 AD=4m,CD=3m,AB=12m,BC=13m,且∠CDA=90°,
求这块草地的面积。
【例 2】勾股定理逆定理的应用
(1)(龙岗)下列条件中,不能判断△ABC 是直角三角形的是( )
A.a:b:c=3:4:5 B.∠A:∠B:∠C=3:4:5
C.∠A+∠B=∠C D.a 2 : b 2 : c 2 3 : 4 : 5
(2)如图,每个小正方形的边长都为 1,△ABC 的顶点都在格点上.
(1)判断△ABC 是什么形状,并说明理由.(2)求△ABC 的面积.
三、进阶训练
1.下面能够成直角三角形三边长的是( )
A.5,6,7 B.5,12,13 C.1,4,9 D.5,11,12
2.分别满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为 1︰2︰3 B.三边长的平方之比为 1︰2︰3
C.三边长之比为 3︰4︰5 D.三内角之比为 3︰4︰5
3.已知三角形三边长为 a、b、c,如果(a 5)2 + b 12 + c2-26c+169=0,则△
ABC 是( )
A.以 a 为斜边的直角三角形 B.以 b 为斜边的直角三角形
C.以 c 为斜边的直角三角形 D.不是直角三角形
4.若在一直角三角形中一直角边与斜边分别为 12、13,则面积为_____,斜边上
的高为______.
5.在△ABC 中,BC=10,AB=13,中线 AD=12,则 AC=________.
6.(龙岗)在 Rt△ABC 中,∠C=90°,AC=9,BC=12,则点 C到 AB 的距离是 7.
在△ABC 中,∠C=90°,两直角边长之比为 3:4,斜边长为 25,则这个三角形的
面积是________.
7.如图,小方格都是边长为 1的正方形,求四边形 ABCD 的面积________.
D
A
C
B
第 7 题图 第 8题图 第 9 题图
8.如图,在四边形 ABCD 中,∠B=∠D=90°,AB=BC=2,CD=1,求 AD 的长.
9.(罗湖)如图,有一块直角三角形纸片,两直角边 AC=6cm,BC=8cm,现将直
角边 AC 沿着直线 AD 折叠,使它落在斜边 AB 上,且与 AE 重合,则 CD 的长为
_______cm.
10.如图,在正方形网格中,每个小正方形的边长均为 1,点 A、B、C、D 均在
格点上.
(1)图中线段 BC 的长度平方为 ;
(2)求图中格点四边形 ABCD 的面积.
11.如图,正方形网格的每个小方格都是边长为 1的正方形,△ABC 的顶点都在
格点上.(1)试判断△ABC 是什么三角形,并说明理由.(2)求△ABC 的面积.
1.3 勾股定理的应用(1)
�
一、激活思维
A
c
b
C a B
定理条件 定理结论 应用
勾股定理
勾股定理逆定理
二.探究新知
探究 1:如右图:有一个圆柱,它的高等于 12 厘米,底面半径等于 3厘米,
在圆柱下底面上的 A点有一只蚂蚁,它想从点 A爬到点 B , 蚂蚁沿着圆柱
侧面爬行的最短路程是多少 (π的值取 3)
(1)想一想,尝试从 A到 B沿圆柱的侧面画出几条路线,你觉得
从 A点到 B点哪条路线最短? B
A
(2)如图,将圆柱侧面剪开展成一个长方形,从 A点到 B点最短路线是什么?
B B
A
A
(3)蚂蚁从 A点出发,想吃到 B 点上的食物,他沿圆柱侧面爬行的最短路程是
多少?
�
A
c
b
C a B
������
A
c
b
C a B
探究 2:如图,长方体的长为 3cm,宽为 2cm,高为 4cm,点 B到点 C的距离为
1cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点 B,需要爬行的最短距离
是?
三、分层反馈
1.一个底面周长为 10cm,高为 12cm 的圆柱,有一只小虫从底部点 A 处爬到上
底 B 处,则小虫所爬的最短路径长是 cm.
2.如图 1,有一圆柱,它的高等于 8cm,底面直径等于 4cm(π=3),在圆柱下
底面的 A 点有一只蚂蚁,它想吃到上底面与 A 相对的 B 点处的食物,需要爬
行的最短路程大约( )
A.10cm B.12cm C.19cm D.20cm
3.如图,正方体的棱长为 2,B为一条棱的中点.已知蚂蚁沿正方体的表面从 A
点出发,到达 B点,则它运动的最短路程为
4.(★)如图,长方体的高为 3cm,底面是正方形且边长为 2cm,现有一只蚂蚁
从 A点出发,沿长方体表面到达 C点,求蚂蚁行走的最短路线.
1.3 勾股定理与逆定理的应用(2)
�
一、激活思维
A
c
b
C a B
定理条件 定理结论 应用
勾股定理
勾股定理逆定理
二.探究新知
探究 1:如图,李叔叔想要检测雕塑底座正面的 AD 和 BC 是否分别垂直于底边
但他随身只带了有刻度的卷尺,李叔叔量得 AD 长 30 厘米,AB 长 40 厘米,BD
长 50 厘米,则 AD 边垂直于 AB 边吗?
探究 2:如图,滑杆在机械槽内运动,∠ACB 为直角,已知滑杆 AB 长 2.5 米,顶
端 A在 AC 上运动,量得滑杆下端 B距 C点的距离为 1.5 米,当端点 B向右移动
0.5 米时,求滑杆顶端 A下滑多少米?
探究 3:如图,甲、乙两船同时从 A 港口出发,甲船以每小时 30 海里的速度向
西偏北 32°的方向航行 2小时到达 C岛,乙船以每小时 40 海里的速度航行 2
小时到 B岛,已知 B、C两岛相距 100 海里,求乙船航行的方向.
三.分层反馈
�
A
c
b
C a B
������
A
c
b
C a B
1.如图 2,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测
量了下,发现 AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检
验一下挖的是否合格?
2.有一个水池,水面是一个边长为 10 尺的正方形,在水池正中央有一根新生的芦
苇,它高出水面 1 尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,
请问这个水池的深度和这根芦苇的长度各是多少
3.如图是一个三级台阶,它的每一级的长、宽、高分别为 20dm、3dm、2dm.A
和 B 是这个台阶上两个相对的端点,点 A 处有一只蚂蚁,想到点 B 处去吃可
口的食物,则蚂蚁沿着台阶面爬行到点 B的最短路程为?
4.(★)如图,将长方形 ABCD 边 AD 沿折痕 AE 折叠,使点 D 落在 BC 上的点 F
处,已知 AB=6,△ABF 的面积是 24,求 DE 的长.
5.如图,有一艘货船和一艘客船同时从港口 A 出发,客船每小时比货船多走 5
海里,客船与货船速度的比为 4:3,货船沿东偏南 10°方向航行,2小时后
货船到达 B处,客船到达 C处,若此时两船相距 50 海里.(1)求两船的速度
分别是多少?(2)求客船航行的方向.
习题课:勾股定理与折叠综合运用
一、知识方法
(1)勾股定理:如果直角三角形的两条直角边长分别是 a,b,斜边长为 c,那
么 .
(2)折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的 和
不变,位置变化, 和 相等.
二、典例精讲
例 1:(三角形)如图,点 D 在△ABC 的边 AC 上,将△ABC 沿 BD 翻折后,点 A恰
好与点 C重合,若 BC=5,CD=3,则 BD 的长
例 2:(长方形)如图,在长房形纸片 ABCD 中,AB=12,BC=5,点 E在 AB 上,
将△DAE 沿 DE 折叠,使点 A落在对角线 BD 上的点 A′处,则 AE 的长
例 3:(正方形)如图,将边长为 8cm 正方形纸片 ABCD 折叠,使点 D 落在 BC 边
的中点 E处,点 A落在点 F处,折痕为 MN,则线段 CN 的长
三、进阶训练
1.如图,在△ABC 中,∠C=90°,将△ACE 沿着 AE 折叠以后 C 点正好落在 AB
边上的点 D处.
(1)当∠B=28°时,求∠AEC 的度数;
(2)当 AC=6,AB=10 时,①求线段 BC 的长;②求线段 DE 的长.
2.如图,在长方形 ABCD 中,AB=3,BC=5,在 CD 上任取一点 E,连接 BE,将
△BCE 沿 BE 折叠,使点 C恰好落在 AD 边上的点 F处,则 CE 的长为( )
A.2 B. C.1 D.
3.如图,将边长为 8cm 的正方形纸片 ABCD 折叠,使点 D落在 AB 边中点 E处,点
C落在点 Q处,折痕为 FH,则线段 AF 的长是( )
A.3cm B.4cm C.5cm D.6cm
4.如图,长方形 ABCD 中,AB=4,BC=3,将其沿直线 MN 折叠,使点 C 与点 A
重合,则 CN 的长
5.如图,长方形 ABCD 中,点 E 在边 AB 上,将矩形 ABCD 沿直线 DE 折叠,点 A
恰好落在边 BC 的点 F处.若 AE=10,BF=6,则 CD 的长
单元复习课 1:勾股定理及其应用
一、问题导思
问题 1:直角三角形的边、角之间分别存在着什么关系
问题 2:举例说明:如何判断一个三角形是否为直角三角形?
问题 3:举例说明:运用勾股定理可以解决那些问题?
问题 4:搜集并列举勾股定理的有关历史。
二、知识建构
问题 5:梳理本章内容,用适当的方式(可以用表格、思维导图、列要点)呈现
全章知识结构。
三、考点精讲
考点 1:勾股定理与面积
例 1:如图,方格纸上每个小正方形的面积为 1个单位.
(1)在方格纸上,以线段 AB 为边画正方形并计算所画正方形的面积,解释
你的计算方法.
(2)你能在图上画出面积依次为 5 个单位、10 个单位、13 个单位的正方形
吗?
考点 2:勾股定理的计算
例 2:如图 BC 长为 3cm,AB 长为 4cm,AF 长为 12cm,正方形 CDEF 的面积=
例 3:如图,在一只底面半径为 3cm,高为 8cm 的圆柱体状水杯中放入一支 13cm
长的吸管,这支吸管露出杯口的长度=
考点 3:判断直角三角形
例 4:相传,古埃及人用 13 个等距的结把一根绳子分成等长的 12 段.并把它摆
成△ABC 的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直
角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,
并说明理由.
例 5:五根小木棒,其长度分别为 7,15,20,24,25,现将它们摆成两个直角
三角形,如图,其中正确的是( )
A B C D
考点 4:勾股定理的应用
40
例 6:如图,一个底面直径为 cm,高为 30cm 的糖罐子,一只蚂蚁从 A处沿着
糖罐的表面爬行到 B处,则蚂蚁爬行的最短距离是
例 7:如图是一个滑梯示意图,若将滑梯 AC 水平放置,则刚好与 AB 一样长.已
知滑梯的高度 CE=3m,CD=1m,求滑道 AC 的长= .
四、易错突破
易错 1: C 不一定是直角
例:在Rt ABC 中,若 AC=3,BC=4,则AB 2 .
易错 2:三角形不一定是直角三角形
例:在 ABC 中, A, B, C 所对的边分别是a,b,c ,且a 3,b 4,若三边长
为连续整数,则 c= .
易错 3:忽略展开图的多种情况
例:如图,长方体的长为 15,宽为 10,高为 20,点 B离点 C的距离是 5,一只
蚂蚁如果要沿着长方体的表面从点 A爬到点 B,需要爬行的最短距离是多少?
易错 4:忽略多图情况
例:(★)在△ABC 中,AB=15,AC=20,BC 边上的高 AD=12,试求 BC 的长.
五、达标测试(时间 25 分钟,满分 50 分;客观题每题 3 分,分数: )
1.如果直角三角形的两直角边长是 9,12,那么斜边长为( )
A.15 B.13 C.17 D.19
2.满足下列条件的△ABC,不是直角三角形的是( )
2 2 2
A.b =c ﹣a B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=12:13:15
3.下面说法正确的是( )
2 2 2
A.在 Rt△ABC 中,a +b =c
B.在 Rt△ABC 中,a=3,b=4,那么 c=5
C.直角三角形两直角边都是 5,那么斜边长为 10
D.直角三角形中,斜边最长
4.如果把直角三角形的两条直角边同时扩大到原来的 2 倍,那么斜边扩大到原
来的( )
A.1倍 B.2倍 C.3倍 D.4倍
5.木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据不符合
直角三角形的三边长的是( )
A.3,4,5 B.6,8,10 C.5,12,13 D.13,16,18
6.如图,将一根长为 8cm(AB=8cm)的橡皮筋水平放置在桌面上,固定两端 A
和 B,然后把中点 C 竖直地向上拉升 3cm 至 D 点,则拉长后橡皮筋的长度为
( )
A.8cm B.10cm C.12cm D.15cm
7.如图是某地的长方形广场的示意图,如果小明要从 A 角走到 C角,那么至少
要走( )
A.90m B.100m C.120m D.140m
8.如图,一圆柱高 5cm,底面半径 4cm,一只蚂蚁从点 A爬到点 B处吃食,要爬
行的最短路程(π取 3)是( )
A.13cm B.26cm C.17cm D.9cm
9.在 Rt△ABC 中,∠B=90°,a=3cm,b=4cm,则第三边的平方是 .
10.如图,在△ABC 中,∠ACB=90°,BC=6,AC=8,CD⊥AB,垂足为 D.则
CD 的长为 .
11.(4 分)已知在 Rt△ABC 中,∠C=90°,AB=10,BC=8,求 AC 的长.
12.(4 分)如图,在 Rt△ABC 中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足
为 D,求 AB 和 CD.
13.(6 分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了
避免走散,他们用两部对话机联系,已知对话机的有效距离为 15 千米,早晨
8:00 甲先出发,他以 6 千米/时的速度向东行走,1 小时后乙出发,他以 5
千米/时的速度向北行进,上午 10:00,甲、乙二人相距多远?还能保持联系
吗?
14.(6 分)观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…,
a,b,c
根据你发现的规律,请写出
(1)当 a=19 时,求 b、c的值;
(2)当 a=2n+1 时,求 b、c的值;
(3)用(2)的结论判断 15,111,112 是否为一组勾股数,并说明理由.
单元错题笔记
题号 错题与错解 错因与正解
题号 错题与错解 错因与正解
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
