3.1圆 同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
3.1圆
一、填空题
1.如图,A,,是上三点,,,则的大小为 .
2.若是半径为的上两个不同的点,则弦的最大值是 .
3.点与圆的位置关系有点在圆内,点在圆 ,点在圆 三种,可以用点到 的距离和半径的大小关系来判断.
4.如图,AB是半径为2的的弦,点C是上的一个动点,若点M,N分别是AB,BC中点,则MN长的最大值是 .
5.如图,AB、CD是⊙O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB=
6.如图,在矩形中,,是线段上一动点,点,绕点逆时针旋转得到点,,若在运动过程中的度数最大值恰好为,则的长度为 .
二、单选题
7.已知点P在半径为8的⊙O外,则( )
A.OP>8 B.OP=8 C.OP<8 D.OP≠8
8.在同一平面内,已知的半径为,,则点P与的位置关系是( )
A.点P在外 B.点P在上 C.点P在内 D.无法确定
9.下列图形为圆的是( )
A. B. C. D.
10.已知的半径为8cm,点到圆心的距离为10cm,则点和的位置关系是( )
A.点在内 B.点在上 C.点在外 D.无法判断
11.已知的半径为3,点P到圆心O的距离为2,则点P与的位置关系是( )
A.点P在外 B.点P在上 C.点P在内 D.无法确定
12.下面说法正确的是( )
1)直径是弦;(2)弦是直径;(3)半圆是弧;(4)弧是半圆.
A.(1)(2) B.(2)(3) C.(3)(4) D.(1)(3)
13.下列说法正确的有( )
①半径相等的两个圆是等圆;②半径相等的两个半圆是等弧;
③过圆心的线段是直径;④分别在两个等圆上的两条弧是等弧.
A.1个 B.2个 C.3个 D.4个
14.已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
15.下列说法中,不正确的是( )
A.直径是弦,弦是直径
B.半圆周是弧
C.圆上的点到圆心的距离都相等
D.同圆或等圆中,优弧一定比劣弧长
16.已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;②若α:β:γ=1:4:3,则∠ACB=30°;③若β<α,β<γ,则α+γ﹣β=90°;④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A.①② B.③④ C.①②③ D.①②③④
三、解答题
17.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
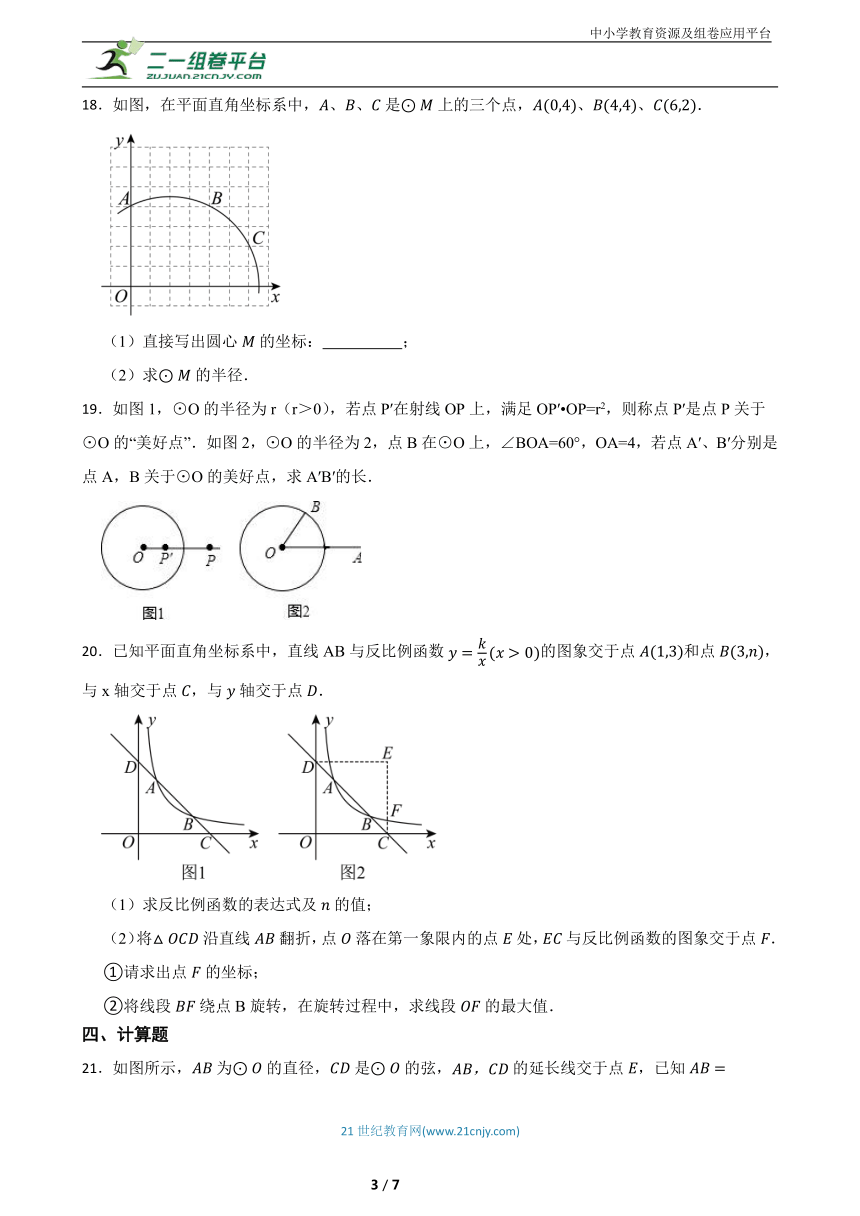
18.如图,在平面直角坐标系中,、、是上的三个点,、、.
(1)直接写出圆心的坐标: ;
(2)求的半径.
19.如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.
20.已知平面直角坐标系中,直线AB与反比例函数的图象交于点和点,与x轴交于点,与轴交于点.
(1)求反比例函数的表达式及的值;
(2)将沿直线翻折,点落在第一象限内的点处,与反比例函数的图象交于点.
①请求出点的坐标;
②将线段绕点B旋转,在旋转过程中,求线段的最大值.
四、计算题
21.如图所示,为的直径,是的弦,的延长线交于点,已知.求的度数.
22.数学兴趣小组探究平面内横、纵坐标满足特定关系的动点的运动轨迹问题:
(1)组长提出问题:动点随着t的变化形成的运动轨迹是什么
甲同学的思考:t取3个特殊值得到3个点坐标,发现3点在一条直线上,可以利用待定系数法求出该直线的表达式;乙同学的思考:令,,通过消去t得到y与x的函数关系式.
______(填甲或乙)同学的方法更严谨,点运动轨迹的函数表达式为______;
(2)如图,在平面直角坐标系中,已知点,,Q为坐标系内一点且,点M从点A出发以每秒8个单位的速度沿x轴向左运动,同时点N从点O出发以每秒6个单位的速度沿y轴向上运动,点P是MN的中点,设运动时间为t.求点P的运动轨迹的函数表达式,并计算当时PQ的最小值;
(3)老师给出坐标平面内两个动点:,.
丙学说:点T、K的运动轨迹都是直线;丁同学说:点T、K在运动过程中不可能重合;请你判断两人结论是否正确并说明理由.
答案解析部分
1.【答案】
【知识点】等腰三角形的性质;圆的相关概念
2.【答案】20
【知识点】圆的相关概念
3.【答案】上;外;圆心
【知识点】点与圆的位置关系
4.【答案】2
【知识点】圆的相关概念;三角形的中位线定理
5.【答案】108°
【知识点】圆的相关概念
6.【答案】
【知识点】两点之间线段最短;勾股定理;点与圆的位置关系;旋转的性质
7.【答案】A
【知识点】点与圆的位置关系
8.【答案】A
【知识点】点与圆的位置关系
9.【答案】B
【知识点】圆的相关概念
10.【答案】C
【知识点】点与圆的位置关系
11.【答案】C
【知识点】点与圆的位置关系
12.【答案】D
【知识点】圆的相关概念
13.【答案】B
【知识点】圆的相关概念
14.【答案】A
【知识点】点与圆的位置关系
15.【答案】A
【知识点】圆的相关概念
16.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;圆的相关概念
17.【答案】解:⑴当d=4cm时,
∵d∴点P在圆内;
⑵当d=5cm时,
∵d=r,
∴点P在圆上;
⑶当d=6cm时,
∵d>r,
∴点P在圆外.
【知识点】点与圆的位置关系
18.【答案】(1)
(2)的半径为
【知识点】勾股定理;圆的相关概念
19.【答案】解:设OA交⊙O于C,连结B′C,如图2,
∵OA′ OA=22,
而r=2,OA=4,
∴OA′=1,
∵OB′ OB=22,
∴OB′=2,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′= ,
∴A′B′=2sin60°= .
【知识点】点与圆的位置关系
20.【答案】(1),
(2)①F点坐标为;②线段OF的最大值为
【知识点】反比例函数与一次函数的交点问题;圆的相关概念;旋转的性质
21.【答案】
【知识点】等腰三角形的性质;圆的相关概念
22.【答案】(1)乙,
(2)
(3)丙同学的结论错误;丁同学的说法正确.
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;圆的相关概念;利用二次函数图象判断一元二次方程根的情况
21世纪教育网(www.21cnjy.com)
2 / 7
3.1圆
一、填空题
1.如图,A,,是上三点,,,则的大小为 .
2.若是半径为的上两个不同的点,则弦的最大值是 .
3.点与圆的位置关系有点在圆内,点在圆 ,点在圆 三种,可以用点到 的距离和半径的大小关系来判断.
4.如图,AB是半径为2的的弦,点C是上的一个动点,若点M,N分别是AB,BC中点,则MN长的最大值是 .
5.如图,AB、CD是⊙O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB=
6.如图,在矩形中,,是线段上一动点,点,绕点逆时针旋转得到点,,若在运动过程中的度数最大值恰好为,则的长度为 .
二、单选题
7.已知点P在半径为8的⊙O外,则( )
A.OP>8 B.OP=8 C.OP<8 D.OP≠8
8.在同一平面内,已知的半径为,,则点P与的位置关系是( )
A.点P在外 B.点P在上 C.点P在内 D.无法确定
9.下列图形为圆的是( )
A. B. C. D.
10.已知的半径为8cm,点到圆心的距离为10cm,则点和的位置关系是( )
A.点在内 B.点在上 C.点在外 D.无法判断
11.已知的半径为3,点P到圆心O的距离为2,则点P与的位置关系是( )
A.点P在外 B.点P在上 C.点P在内 D.无法确定
12.下面说法正确的是( )
1)直径是弦;(2)弦是直径;(3)半圆是弧;(4)弧是半圆.
A.(1)(2) B.(2)(3) C.(3)(4) D.(1)(3)
13.下列说法正确的有( )
①半径相等的两个圆是等圆;②半径相等的两个半圆是等弧;
③过圆心的线段是直径;④分别在两个等圆上的两条弧是等弧.
A.1个 B.2个 C.3个 D.4个
14.已知⊙O的直径为3cm,点P到圆心O的距离OP=2cm,则点P( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
15.下列说法中,不正确的是( )
A.直径是弦,弦是直径
B.半圆周是弧
C.圆上的点到圆心的距离都相等
D.同圆或等圆中,优弧一定比劣弧长
16.已知△ABC内接于⊙O,连接OA,OB,OC,设∠OAC=α,∠OBA=β,∠OCB=γ.则下列叙述中正确的有( )
①若α<β,α<γ,且OC∥AB,则γ=90°﹣α;②若α:β:γ=1:4:3,则∠ACB=30°;③若β<α,β<γ,则α+γ﹣β=90°;④若β<α,β<γ,则∠BAC+∠ABC=α+γ﹣2β.
A.①② B.③④ C.①②③ D.①②③④
三、解答题
17.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm,判定点P与圆的位置关系,并说明理由.
18.如图,在平面直角坐标系中,、、是上的三个点,、、.
(1)直接写出圆心的坐标: ;
(2)求的半径.
19.如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′ OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.
20.已知平面直角坐标系中,直线AB与反比例函数的图象交于点和点,与x轴交于点,与轴交于点.
(1)求反比例函数的表达式及的值;
(2)将沿直线翻折,点落在第一象限内的点处,与反比例函数的图象交于点.
①请求出点的坐标;
②将线段绕点B旋转,在旋转过程中,求线段的最大值.
四、计算题
21.如图所示,为的直径,是的弦,的延长线交于点,已知.求的度数.
22.数学兴趣小组探究平面内横、纵坐标满足特定关系的动点的运动轨迹问题:
(1)组长提出问题:动点随着t的变化形成的运动轨迹是什么
甲同学的思考:t取3个特殊值得到3个点坐标,发现3点在一条直线上,可以利用待定系数法求出该直线的表达式;乙同学的思考:令,,通过消去t得到y与x的函数关系式.
______(填甲或乙)同学的方法更严谨,点运动轨迹的函数表达式为______;
(2)如图,在平面直角坐标系中,已知点,,Q为坐标系内一点且,点M从点A出发以每秒8个单位的速度沿x轴向左运动,同时点N从点O出发以每秒6个单位的速度沿y轴向上运动,点P是MN的中点,设运动时间为t.求点P的运动轨迹的函数表达式,并计算当时PQ的最小值;
(3)老师给出坐标平面内两个动点:,.
丙学说:点T、K的运动轨迹都是直线;丁同学说:点T、K在运动过程中不可能重合;请你判断两人结论是否正确并说明理由.
答案解析部分
1.【答案】
【知识点】等腰三角形的性质;圆的相关概念
2.【答案】20
【知识点】圆的相关概念
3.【答案】上;外;圆心
【知识点】点与圆的位置关系
4.【答案】2
【知识点】圆的相关概念;三角形的中位线定理
5.【答案】108°
【知识点】圆的相关概念
6.【答案】
【知识点】两点之间线段最短;勾股定理;点与圆的位置关系;旋转的性质
7.【答案】A
【知识点】点与圆的位置关系
8.【答案】A
【知识点】点与圆的位置关系
9.【答案】B
【知识点】圆的相关概念
10.【答案】C
【知识点】点与圆的位置关系
11.【答案】C
【知识点】点与圆的位置关系
12.【答案】D
【知识点】圆的相关概念
13.【答案】B
【知识点】圆的相关概念
14.【答案】A
【知识点】点与圆的位置关系
15.【答案】A
【知识点】圆的相关概念
16.【答案】A
【知识点】三角形内角和定理;等腰三角形的性质;圆的相关概念
17.【答案】解:⑴当d=4cm时,
∵d
⑵当d=5cm时,
∵d=r,
∴点P在圆上;
⑶当d=6cm时,
∵d>r,
∴点P在圆外.
【知识点】点与圆的位置关系
18.【答案】(1)
(2)的半径为
【知识点】勾股定理;圆的相关概念
19.【答案】解:设OA交⊙O于C,连结B′C,如图2,
∵OA′ OA=22,
而r=2,OA=4,
∴OA′=1,
∵OB′ OB=22,
∴OB′=2,即点B和B′重合,
∵∠BOA=60°,OB=OC,
∴△OBC为等边三角形,
而点A′为OC的中点,
∴B′A′⊥OC,
在Rt△OA′B′中,sin∠A′OB′= ,
∴A′B′=2sin60°= .
【知识点】点与圆的位置关系
20.【答案】(1),
(2)①F点坐标为;②线段OF的最大值为
【知识点】反比例函数与一次函数的交点问题;圆的相关概念;旋转的性质
21.【答案】
【知识点】等腰三角形的性质;圆的相关概念
22.【答案】(1)乙,
(2)
(3)丙同学的结论错误;丁同学的说法正确.
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;圆的相关概念;利用二次函数图象判断一元二次方程根的情况
21世纪教育网(www.21cnjy.com)
2 / 7
