3.3垂径定理 同步练习(含答案)
文档属性
| 名称 | 3.3垂径定理 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 459.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.3垂径定理
一、单选题
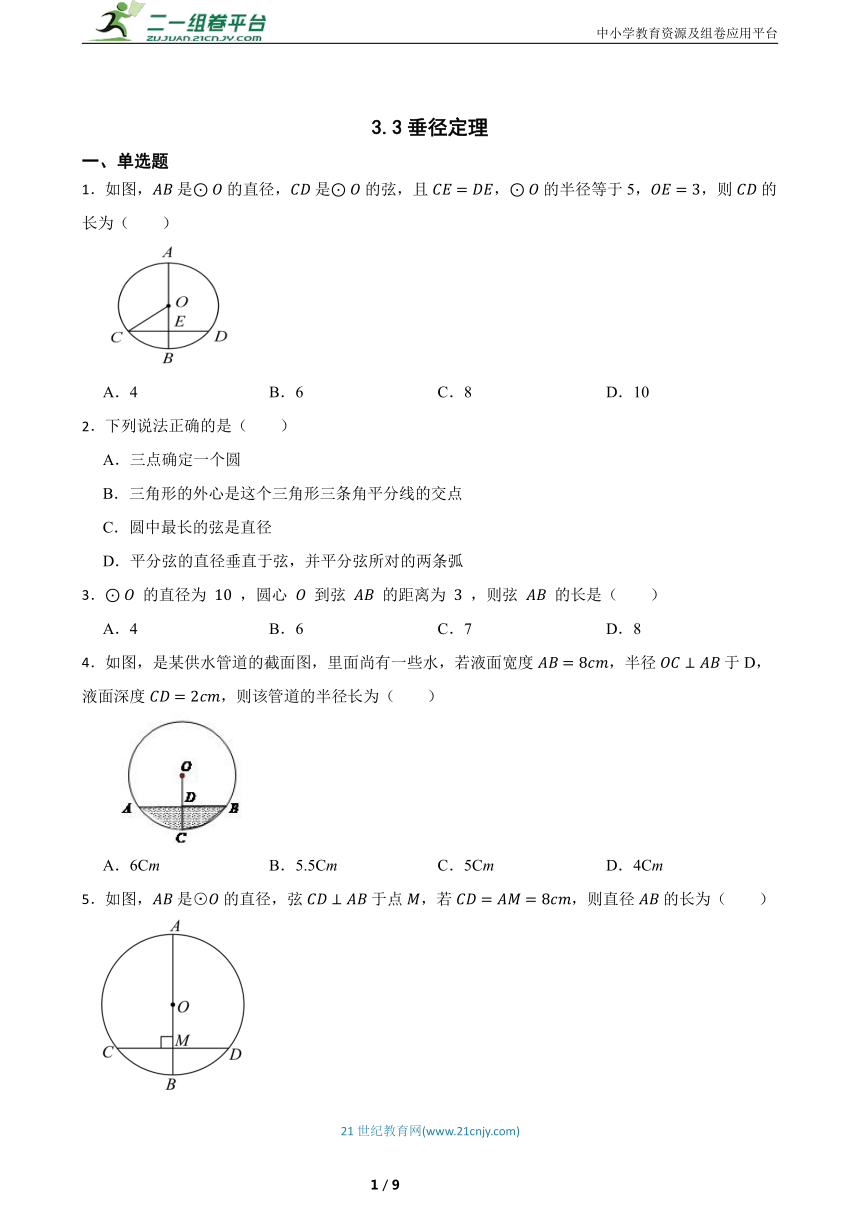
1.如图,是的直径,是的弦,且,的半径等于5,,则的长为( )
A.4 B.6 C.8 D.10
2.下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心是这个三角形三条角平分线的交点
C.圆中最长的弦是直径
D.平分弦的直径垂直于弦,并平分弦所对的两条弧
3. 的直径为 ,圆心 到弦 的距离为 ,则弦 的长是( )
A.4 B.6 C.7 D.8
4.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于D,液面深度,则该管道的半径长为( )
A.6Cm B.5.5Cm C.5Cm D.4Cm
5.如图,是⊙的直径,弦于点,若,则直径的长为( )
A. B. C. D.
6.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的半径为( )
A.5cm B.6cm C.7cm D.8cm
7.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
A.6m B.8m C.10m D.12m
8.如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(7,0),直线y=kx-1恰好平分⊙P的面积,那么k的值是( )
A. B. C.1 D.
9.如图,在 中, 是直径, 是弦, 于点M,若 ,则 的长为( )
A. B. C. D.
10.如图,在平面直角坐标系中,⊙O经过点(0,10),直线y=kx+2k﹣4与⊙O交于B、C两点,则弦BC的最小值是( )
A. B. C. D.以上都不对
二、填空题
11.如图,内接于,,,的半径长等于 .
12.如图,AB是⊙O的弦,OC⊥AB于点D,交⊙O于点C,若⊙O的半径为5,CD=2,那么AB的长为 .
13.如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为 cm.
14.在圆柱形油槽内装有一些油,截面如图,油面宽AB为4分米,如果再注入一些油后,油面AB上升1分米,油面宽变为6分米,圈柱形油槽的直径MN为 .
15.⊙O的半径为10,弦AB//CD,AB=12,CD=16,则AB与CD之间的距离为 .
16.如图,在 中, , , ,过点 作 的平行线 , 为直线 上一动点, 为 的外接圆,直线 交 于 点,则 的最小值为 .
三、计算题
17.如图,是的直径,弦于点E,,若,求的长.
18.一条盘水管的截面如图所示,水面宽垂直平分半径.
(1)求的度数;
(2)若的半径为6,求弦的长.
(3)若连结,请判断四边形的形状,并给出证明.
四、解答题
19.唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦长8m,设圆心为,交水面于点D,轮子的吃水深度为2m,求该桨轮船的轮子直径.
20.如图,AB为⊙O的弦,OC⊥AB于点M,交⊙O于点C.若⊙O的半径为10,OM:MC=3:2,求AB的长.
21.如图所示,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水位上升了10cm,则此时水面宽为多少厘米
22.(1)如图①,,点P在的平分线上,.点E,F分别在边,上,且,连接.求线段的最小值;
(2)如图②,是一个圆弧型拱桥的截面示意图.点是拱桥的中点,桥下水面的宽度,点到水面的距离.点,均在上,,且,在点,处各装有一个照明灯,图中和分别是这两个灯的光照范围.两灯可以分别绕点,左右转动,且光束始终照在水面上.即,可分别绕点,按顺(逆)时针方向旋转(照明灯的大小忽略不计),线段,在上,此时,线段是这两灯照在水面上的重叠部分的水面宽度.已知,在这两个灯的照射下,当整个水面都被灯光照到时,求这两个灯照在水面上的重叠部分的水面宽度.(可利用备用图解答)
答案解析部分
1.【答案】C
【知识点】勾股定理;垂径定理
2.【答案】C
【知识点】圆的相关概念;垂径定理
3.【答案】D
【知识点】垂径定理
4.【答案】C
【知识点】垂径定理的实际应用
5.【答案】D
【知识点】勾股定理;垂径定理
6.【答案】A
【知识点】垂径定理
7.【答案】C
【知识点】勾股定理;垂径定理的实际应用
8.【答案】C
【知识点】待定系数法求一次函数解析式;矩形的判定与性质;垂径定理
9.【答案】B
【知识点】垂径定理
10.【答案】C
【知识点】垂径定理;一次函数的实际应用-几何问题
11.【答案】
【知识点】勾股定理;垂径定理
12.【答案】8
【知识点】垂径定理
13.【答案】1
【知识点】垂径定理
14.【答案】
【知识点】勾股定理;垂径定理
15.【答案】2或14
【知识点】勾股定理;垂径定理
16.【答案】2
【知识点】平行线的性质;等腰三角形的判定与性质;勾股定理;垂径定理
17.【答案】
【知识点】勾股定理;垂径定理
18.【答案】(1)
(2)
(3)菱形
【知识点】等边三角形的判定与性质;菱形的判定;圆的相关概念;垂径定理
19.【答案】该桨轮船的轮子直径为10m
【知识点】勾股定理;垂径定理的实际应用
20.【答案】
【知识点】垂径定理
21.【答案】解:如图,设下雨前水面宽为AB,下雨后水面宽为A'B',连结OB,OB',作半径OD⊥AB于点C,交A'B'于点C',则.
∵A'B'∥AB,OD⊥AB,
∴OC'⊥A'B',
∴A'B'=2B'C',
∵OD⊥AB,
∴.
∵
由勾股定理得OC=40cm,
.
又易知
由勾股定理得B'C'=40cm,
.
答:此时水面宽为80cm.
【知识点】勾股定理;垂径定理的实际应用
22.【答案】(1);(2)或
【知识点】三角形全等及其性质;垂径定理的实际应用;圆心角、弧、弦的关系;解直角三角形
21世纪教育网(www.21cnjy.com)
1 / 9
3.3垂径定理
一、单选题
1.如图,是的直径,是的弦,且,的半径等于5,,则的长为( )
A.4 B.6 C.8 D.10
2.下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心是这个三角形三条角平分线的交点
C.圆中最长的弦是直径
D.平分弦的直径垂直于弦,并平分弦所对的两条弧
3. 的直径为 ,圆心 到弦 的距离为 ,则弦 的长是( )
A.4 B.6 C.7 D.8
4.如图,是某供水管道的截面图,里面尚有一些水,若液面宽度,半径于D,液面深度,则该管道的半径长为( )
A.6Cm B.5.5Cm C.5Cm D.4Cm
5.如图,是⊙的直径,弦于点,若,则直径的长为( )
A. B. C. D.
6.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的半径为( )
A.5cm B.6cm C.7cm D.8cm
7.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
A.6m B.8m C.10m D.12m
8.如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(7,0),直线y=kx-1恰好平分⊙P的面积,那么k的值是( )
A. B. C.1 D.
9.如图,在 中, 是直径, 是弦, 于点M,若 ,则 的长为( )
A. B. C. D.
10.如图,在平面直角坐标系中,⊙O经过点(0,10),直线y=kx+2k﹣4与⊙O交于B、C两点,则弦BC的最小值是( )
A. B. C. D.以上都不对
二、填空题
11.如图,内接于,,,的半径长等于 .
12.如图,AB是⊙O的弦,OC⊥AB于点D,交⊙O于点C,若⊙O的半径为5,CD=2,那么AB的长为 .
13.如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为 cm.
14.在圆柱形油槽内装有一些油,截面如图,油面宽AB为4分米,如果再注入一些油后,油面AB上升1分米,油面宽变为6分米,圈柱形油槽的直径MN为 .
15.⊙O的半径为10,弦AB//CD,AB=12,CD=16,则AB与CD之间的距离为 .
16.如图,在 中, , , ,过点 作 的平行线 , 为直线 上一动点, 为 的外接圆,直线 交 于 点,则 的最小值为 .
三、计算题
17.如图,是的直径,弦于点E,,若,求的长.
18.一条盘水管的截面如图所示,水面宽垂直平分半径.
(1)求的度数;
(2)若的半径为6,求弦的长.
(3)若连结,请判断四边形的形状,并给出证明.
四、解答题
19.唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦长8m,设圆心为,交水面于点D,轮子的吃水深度为2m,求该桨轮船的轮子直径.
20.如图,AB为⊙O的弦,OC⊥AB于点M,交⊙O于点C.若⊙O的半径为10,OM:MC=3:2,求AB的长.
21.如图所示,一下水管道横截面为圆形,直径为100cm,下雨前水面宽为60cm,一场大雨过后,水位上升了10cm,则此时水面宽为多少厘米
22.(1)如图①,,点P在的平分线上,.点E,F分别在边,上,且,连接.求线段的最小值;
(2)如图②,是一个圆弧型拱桥的截面示意图.点是拱桥的中点,桥下水面的宽度,点到水面的距离.点,均在上,,且,在点,处各装有一个照明灯,图中和分别是这两个灯的光照范围.两灯可以分别绕点,左右转动,且光束始终照在水面上.即,可分别绕点,按顺(逆)时针方向旋转(照明灯的大小忽略不计),线段,在上,此时,线段是这两灯照在水面上的重叠部分的水面宽度.已知,在这两个灯的照射下,当整个水面都被灯光照到时,求这两个灯照在水面上的重叠部分的水面宽度.(可利用备用图解答)
答案解析部分
1.【答案】C
【知识点】勾股定理;垂径定理
2.【答案】C
【知识点】圆的相关概念;垂径定理
3.【答案】D
【知识点】垂径定理
4.【答案】C
【知识点】垂径定理的实际应用
5.【答案】D
【知识点】勾股定理;垂径定理
6.【答案】A
【知识点】垂径定理
7.【答案】C
【知识点】勾股定理;垂径定理的实际应用
8.【答案】C
【知识点】待定系数法求一次函数解析式;矩形的判定与性质;垂径定理
9.【答案】B
【知识点】垂径定理
10.【答案】C
【知识点】垂径定理;一次函数的实际应用-几何问题
11.【答案】
【知识点】勾股定理;垂径定理
12.【答案】8
【知识点】垂径定理
13.【答案】1
【知识点】垂径定理
14.【答案】
【知识点】勾股定理;垂径定理
15.【答案】2或14
【知识点】勾股定理;垂径定理
16.【答案】2
【知识点】平行线的性质;等腰三角形的判定与性质;勾股定理;垂径定理
17.【答案】
【知识点】勾股定理;垂径定理
18.【答案】(1)
(2)
(3)菱形
【知识点】等边三角形的判定与性质;菱形的判定;圆的相关概念;垂径定理
19.【答案】该桨轮船的轮子直径为10m
【知识点】勾股定理;垂径定理的实际应用
20.【答案】
【知识点】垂径定理
21.【答案】解:如图,设下雨前水面宽为AB,下雨后水面宽为A'B',连结OB,OB',作半径OD⊥AB于点C,交A'B'于点C',则.
∵A'B'∥AB,OD⊥AB,
∴OC'⊥A'B',
∴A'B'=2B'C',
∵OD⊥AB,
∴.
∵
由勾股定理得OC=40cm,
.
又易知
由勾股定理得B'C'=40cm,
.
答:此时水面宽为80cm.
【知识点】勾股定理;垂径定理的实际应用
22.【答案】(1);(2)或
【知识点】三角形全等及其性质;垂径定理的实际应用;圆心角、弧、弦的关系;解直角三角形
21世纪教育网(www.21cnjy.com)
1 / 9
