3.4圆心角和圆周角的关系 同步练习(含答案)
文档属性
| 名称 | 3.4圆心角和圆周角的关系 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 391.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 19:16:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.4圆心角和圆周角的关系
一、单选题
1.如图,点 , , 在⊙O上, ,则 的度数为( )
A. B. C. D.
2.如图,四边形ABCD内接于⊙O,若∠BCD=110°,则∠BOD的度数为( )
A.35° B.70° C.110° D.140°
3.如图,点 为 上三点, ,则 的度数等于( )
A. B. C. D.
4.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )
A.100° B.110° C.120° D.130°
5.如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内 上的一点,若 ,则 的度数是
A. B. C. D.
6.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠BAD=20°,则∠BOC等于()
A.20° B.40° C.50° D.60°
7.如图,点A、B、C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
8.如图,在△ABC中,以BC为直径的半圆O,分别交AB,AC于点D,E,连接OD,OE,若∠A=α,则∠DOE的度数为( )
A.180-2α B.180-α C.90-α D.2a
9.已知:正方形ABCD内接于⊙O,点P是⊙O上不同于点B、C的任意一点,则∠BPC的度数是( ).
A.45° B.90° C.135° D.45°或135°
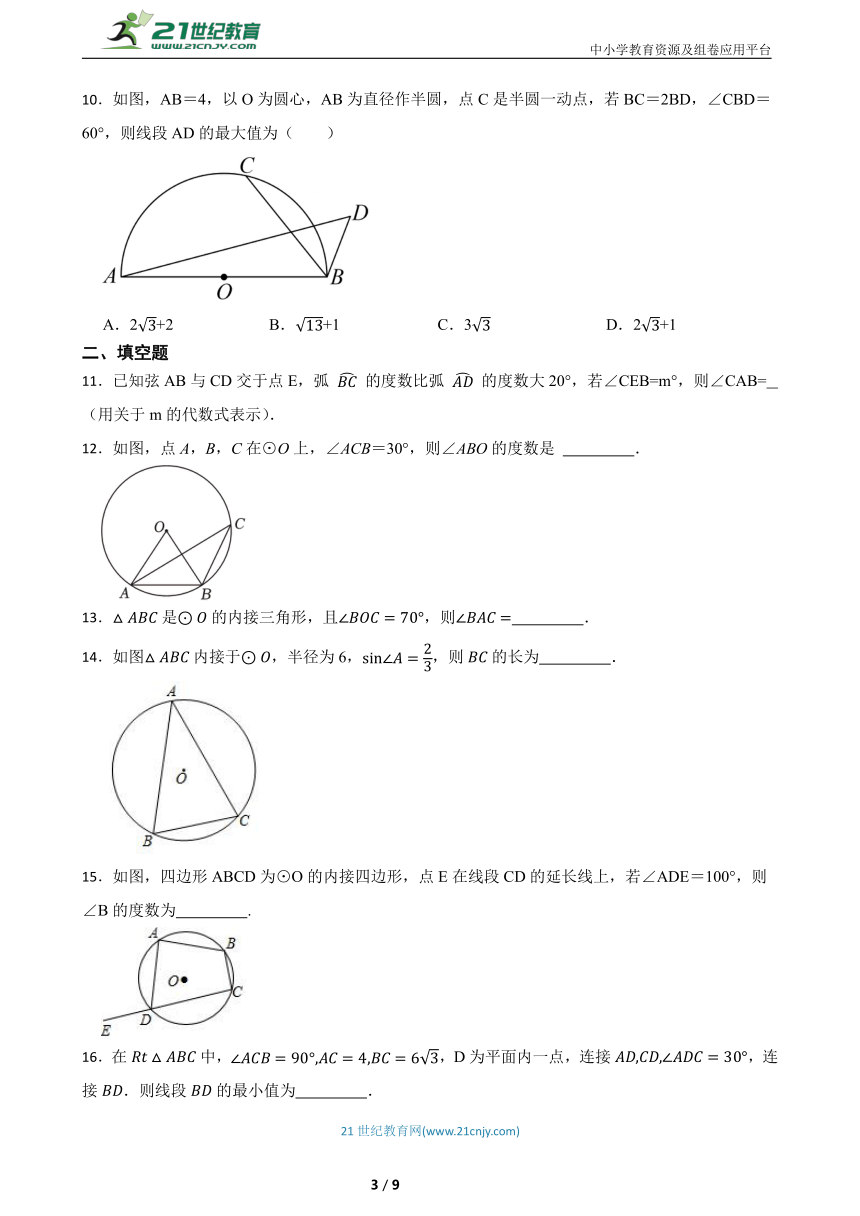
10.如图,AB=4,以O为圆心,AB为直径作半圆,点C是半圆一动点,若BC=2BD,∠CBD=60°,则线段AD的最大值为( )
A.2+2 B.+1 C.3 D.2+1
二、填空题
11.已知弦AB与CD交于点E,弧 的度数比弧 的度数大20°,若∠CEB=m°,则∠CAB= (用关于m的代数式表示).
12.如图,点A,B,C在⊙O上,∠ACB=30°,则∠ABO的度数是 .
13.是的内接三角形,且,则 .
14.如图内接于,半径为6,,则的长为 .
15.如图,四边形ABCD为⊙O的内接四边形,点E在线段CD的延长线上,若∠ADE=100°,则∠B的度数为 .
16.在中,,D为平面内一点,连接,连接.则线段的最小值为 .
三、计算题
17.如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=150°,求∠EBC的度数.
18.如图,已知都是的半径,.
(1)若,求的度数.
(2)若,求的半径.
19.如图①,点,在线段上,点在点的左侧,若线段,,满足,称,是线段的勾股点.
(1)如图②,,是线段的勾股点,分别以线段,,为边向的同侧作正,正,正,已知正、正的面积分别是3,5,则正的面积是 ;
(2)如图①,,,是线段的勾股点,当时,求的长;
(3)如图③,,是线段的勾股点,以为直径画,在上,,连接,,若,求的度数.
四、解答题
20.如图,P为圆外一点,PA交圆于点A,B,PC交圆于点C,D,的度数为30°,的度数为80°.求∠P的度数.
21.如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
22.如图所示, 的直径 为 弦 为 的平分线交于 于点 求 的长.
23.如图,在平面直角坐标系中,点O是原点,直线 分别交x轴、y 轴于点B、A,
(1)如图1, 求b的值:
(2)如图2,点C 在 x轴正半轴上, ,点 D 在直线上方, 设点C的横坐标为t,四边形的面积为S,求S和t的函数关系式:
(3)如图3,在(2)的条件下,过点D作 轴于点 F, 连接, 点G为上一点, 连接, 于点H, 连接, 连接,,求直线的解析式.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】D
【知识点】圆内接四边形的性质
3.【答案】C
【知识点】圆周角定理
4.【答案】B
【知识点】圆周角定理
5.【答案】D
【知识点】等腰三角形的性质;圆周角定理
6.【答案】B
【知识点】垂径定理的实际应用;圆周角定理
7.【答案】B
【知识点】等边三角形的判定与性质;平行四边形的性质;圆周角定理
8.【答案】A
【知识点】三角形内角和定理;圆周角定理
9.【答案】D
【知识点】正方形的性质;圆周角定理;圆内接四边形的性质
10.【答案】B
【知识点】三角形三边关系;等边三角形的判定与性质;勾股定理;圆周角定理;直角三角形斜边上的中线
11.【答案】
【知识点】三角形的外角性质;圆周角定理
12.【答案】60°
【知识点】圆周角定理
13.【答案】
【知识点】圆周角定理
14.【答案】8
【知识点】圆周角定理;解直角三角形
15.【答案】100°
【知识点】圆内接四边形的性质
16.【答案】-4
【知识点】圆的相关概念;垂径定理;圆周角定理;三角形的中位线定理
17.【答案】
【知识点】圆周角定理;圆内接四边形的性质
18.【答案】(1)
(2)
【知识点】垂径定理;圆心角、弧、弦的关系;圆周角定理
19.【答案】(1)2
(2)5
(3)
【知识点】等边三角形的性质;勾股定理;圆周角定理;解直角三角形
20.【答案】解: ∵的度数为30°,的度数为80°
∴∠ABC=40° ,∠BCD=15°,
∴∠P=∠ABC-∠BCD= 25°.
【知识点】三角形的外角性质;圆周角定理
21.【答案】(1)60°;(2)5.
【知识点】垂径定理;圆周角定理
22.【答案】解: 是直径,
,
在 中, , , ,
.
,
又 平分 ,
,
,
,
又在 中, ,
,
.
【知识点】勾股定理;圆心角、弧、弦的关系;圆周角定理
23.【答案】(1)8
(2)
(3)
【知识点】等腰三角形的判定与性质;圆周角定理;解直角三角形;一次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
1 / 9
3.4圆心角和圆周角的关系
一、单选题
1.如图,点 , , 在⊙O上, ,则 的度数为( )
A. B. C. D.
2.如图,四边形ABCD内接于⊙O,若∠BCD=110°,则∠BOD的度数为( )
A.35° B.70° C.110° D.140°
3.如图,点 为 上三点, ,则 的度数等于( )
A. B. C. D.
4.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )
A.100° B.110° C.120° D.130°
5.如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内 上的一点,若 ,则 的度数是
A. B. C. D.
6.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠BAD=20°,则∠BOC等于()
A.20° B.40° C.50° D.60°
7.如图,点A、B、C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
8.如图,在△ABC中,以BC为直径的半圆O,分别交AB,AC于点D,E,连接OD,OE,若∠A=α,则∠DOE的度数为( )
A.180-2α B.180-α C.90-α D.2a
9.已知:正方形ABCD内接于⊙O,点P是⊙O上不同于点B、C的任意一点,则∠BPC的度数是( ).
A.45° B.90° C.135° D.45°或135°
10.如图,AB=4,以O为圆心,AB为直径作半圆,点C是半圆一动点,若BC=2BD,∠CBD=60°,则线段AD的最大值为( )
A.2+2 B.+1 C.3 D.2+1
二、填空题
11.已知弦AB与CD交于点E,弧 的度数比弧 的度数大20°,若∠CEB=m°,则∠CAB= (用关于m的代数式表示).
12.如图,点A,B,C在⊙O上,∠ACB=30°,则∠ABO的度数是 .
13.是的内接三角形,且,则 .
14.如图内接于,半径为6,,则的长为 .
15.如图,四边形ABCD为⊙O的内接四边形,点E在线段CD的延长线上,若∠ADE=100°,则∠B的度数为 .
16.在中,,D为平面内一点,连接,连接.则线段的最小值为 .
三、计算题
17.如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=150°,求∠EBC的度数.
18.如图,已知都是的半径,.
(1)若,求的度数.
(2)若,求的半径.
19.如图①,点,在线段上,点在点的左侧,若线段,,满足,称,是线段的勾股点.
(1)如图②,,是线段的勾股点,分别以线段,,为边向的同侧作正,正,正,已知正、正的面积分别是3,5,则正的面积是 ;
(2)如图①,,,是线段的勾股点,当时,求的长;
(3)如图③,,是线段的勾股点,以为直径画,在上,,连接,,若,求的度数.
四、解答题
20.如图,P为圆外一点,PA交圆于点A,B,PC交圆于点C,D,的度数为30°,的度数为80°.求∠P的度数.
21.如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
22.如图所示, 的直径 为 弦 为 的平分线交于 于点 求 的长.
23.如图,在平面直角坐标系中,点O是原点,直线 分别交x轴、y 轴于点B、A,
(1)如图1, 求b的值:
(2)如图2,点C 在 x轴正半轴上, ,点 D 在直线上方, 设点C的横坐标为t,四边形的面积为S,求S和t的函数关系式:
(3)如图3,在(2)的条件下,过点D作 轴于点 F, 连接, 点G为上一点, 连接, 于点H, 连接, 连接,,求直线的解析式.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】D
【知识点】圆内接四边形的性质
3.【答案】C
【知识点】圆周角定理
4.【答案】B
【知识点】圆周角定理
5.【答案】D
【知识点】等腰三角形的性质;圆周角定理
6.【答案】B
【知识点】垂径定理的实际应用;圆周角定理
7.【答案】B
【知识点】等边三角形的判定与性质;平行四边形的性质;圆周角定理
8.【答案】A
【知识点】三角形内角和定理;圆周角定理
9.【答案】D
【知识点】正方形的性质;圆周角定理;圆内接四边形的性质
10.【答案】B
【知识点】三角形三边关系;等边三角形的判定与性质;勾股定理;圆周角定理;直角三角形斜边上的中线
11.【答案】
【知识点】三角形的外角性质;圆周角定理
12.【答案】60°
【知识点】圆周角定理
13.【答案】
【知识点】圆周角定理
14.【答案】8
【知识点】圆周角定理;解直角三角形
15.【答案】100°
【知识点】圆内接四边形的性质
16.【答案】-4
【知识点】圆的相关概念;垂径定理;圆周角定理;三角形的中位线定理
17.【答案】
【知识点】圆周角定理;圆内接四边形的性质
18.【答案】(1)
(2)
【知识点】垂径定理;圆心角、弧、弦的关系;圆周角定理
19.【答案】(1)2
(2)5
(3)
【知识点】等边三角形的性质;勾股定理;圆周角定理;解直角三角形
20.【答案】解: ∵的度数为30°,的度数为80°
∴∠ABC=40° ,∠BCD=15°,
∴∠P=∠ABC-∠BCD= 25°.
【知识点】三角形的外角性质;圆周角定理
21.【答案】(1)60°;(2)5.
【知识点】垂径定理;圆周角定理
22.【答案】解: 是直径,
,
在 中, , , ,
.
,
又 平分 ,
,
,
,
又在 中, ,
,
.
【知识点】勾股定理;圆心角、弧、弦的关系;圆周角定理
23.【答案】(1)8
(2)
(3)
【知识点】等腰三角形的判定与性质;圆周角定理;解直角三角形;一次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
1 / 9
