3.5确定圆的条件 同步练习(含答案)
文档属性
| 名称 | 3.5确定圆的条件 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 305.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 19:08:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.5确定圆的条件
一、填空题
1.三角形三边垂直平分线的交点到三角形 的距离相等.
2.在一个直角三角形中,两边长分别是5,12,那么这个三角形的外接圆的半径是 .
3.若直角三角形的两直角边长为3、4,则该直角三角形的外接圆半径为 .
4.已知直角三角形的两条直角边长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离为 .
5.已知某直角三角形的边长分别是3cm、4cm,则它的外接圆半径是 cm.
6.如图所示,已知△ABC和△BDE都是等边三角形。下列结论:① AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥ FG∥AD。其中正确的有 个.
二、单选题
7.三角形的外心是( )
A.三条中线的交点 B.三个内角的角平分线的交点
C.三条边的垂直平分线的交点 D.三条高的交点
8.如图是由3个边长为2的正方形组成的物件,将它镶嵌在一个圆形的金属框上,使A,B,C三点恰好在金属框上,则该金属框的半径是( )
A. B. C. D.4
9.如图,将放在每个小正方形的边长为1的网格中,点、、均落在格点上,用一个圆面去覆盖,能够完全覆盖这个三角形的最小圆面的半径是( )
A. B. C.2 D.
10.下列说法正确的是( )
A.相等的角是对顶角
B.对角线相等的四边形是矩形
C.三角形的外心是它的三条角平分线的交点
D.线段垂直平分线上的点到线段两端的距离相等
11.过A,B,C三点能确定一个圆的条件是( )
①AB=2,BC=3,AC=5;②AB=3, BC=3,AC=2;③AB=3,BC=4,AC= 5.
A.①② B.①②③ C.②③ D.①③
12.如图,在由小正方形组成的网格中,点A,B,C,D,E,F,O均在格点上.下列三角形中,外心不是点O的是( )
A. B. C. D.
13.如图,在等腰△ABC中,AB=AC,把△ABC沿EF折叠,点C的对应点为O,连接AO,使AO平分∠BAC,若∠BAC=∠CFE=50°,则点O是( )
A.△ABC的内心 B.△ABC的外心 C.△ABF的内心 D.△ABF的外心
14.下列条件中,能确定一个圆的是( )
A.经过已知点M B.以点O为圆心,长为半径
C.以长为半径 D.以点O为圆心
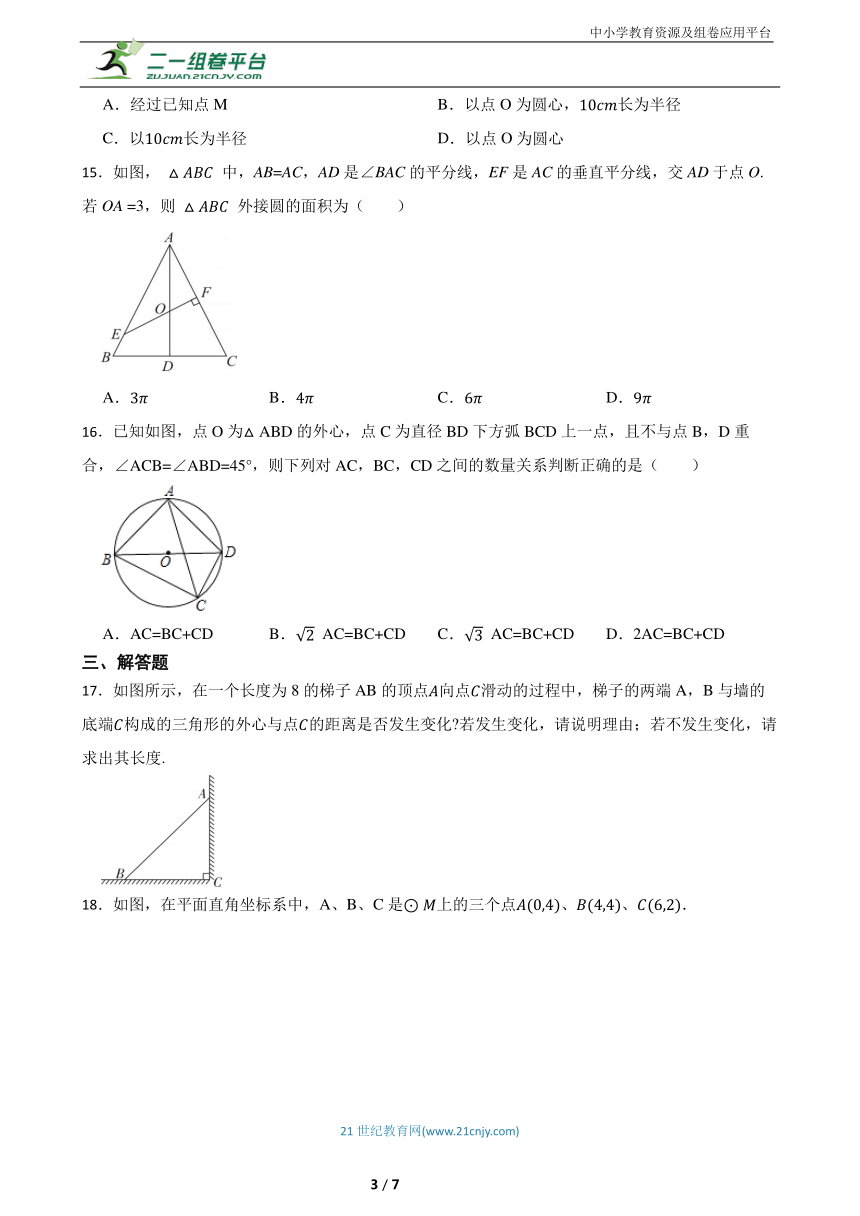
15.如图, 中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA =3,则 外接圆的面积为( )
A. B. C. D.
16.已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
A.AC=BC+CD B. AC=BC+CD C. AC=BC+CD D.2AC=BC+CD
三、解答题
17.如图所示,在一个长度为8的梯子AB的顶点向点滑动的过程中,梯子的两端A,B与墙的底端构成的三角形的外心与点的距离是否发生变化 若发生变化,请说明理由;若不发生变化,请求出其长度.
18.如图,在平面直角坐标系中,A、B、C是上的三个点、、.
(1)写出圆心M的坐标为___________;
(2)这个圆的半径为___________;
(3)直接判断点与的位置关系.点在__________(填内、外、上).
19.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是
20.【问题提出】
(1)如图1,在边长为的等边中,点在边上,,连接,则的面积为____
【问题探究】
(2)如图2,已知在边长为的正方形中,点在边上,点在边上,且,若,求的面积;
【问题解决】
(3)如图3是我市华南大道的一部分,因自来水抢修,需要在米,米的矩形区域内开挖一个的工作面,其中、分别在、边上不与点、、重合,且,为了减少对该路段的交通拥堵影响,要求面积最小,那么是否存在一个面积最小的若存在,请求出面积的最小值;若不存在,请说明理由.
答案解析部分
1.【答案】三个顶点
【知识点】三角形的外接圆与外心
2.【答案】6或
【知识点】勾股定理;圆的相关概念;三角形的外接圆与外心;直角三角形斜边上的中线
3.【答案】
【知识点】勾股定理;三角形的外接圆与外心
4.【答案】
【知识点】勾股定理;三角形的外接圆与外心;三角形的重心及应用
5.【答案】2或2.5
【知识点】三角形的外接圆与外心
6.【答案】6
【知识点】全等三角形的判定与性质;等边三角形的判定与性质;圆周角定理;确定圆的条件
7.【答案】C
【知识点】三角形的外接圆与外心
8.【答案】A
【知识点】勾股定理;圆周角定理;确定圆的条件
9.【答案】D
【知识点】三角形的外接圆与外心
10.【答案】D
【知识点】线段垂直平分线的性质;矩形的判定;三角形的外接圆与外心;对顶角及其性质
11.【答案】C
【知识点】确定圆的条件
12.【答案】C
【知识点】三角形的外接圆与外心
13.【答案】B
【知识点】三角形的外接圆与外心
14.【答案】B
【知识点】确定圆的条件
15.【答案】D
【知识点】等腰三角形的性质;三角形的外接圆与外心
16.【答案】B
【知识点】全等三角形的判定与性质;三角形的外接圆与外心
17.【答案】解:不发生变化,理由如下:
∵梯子的两端A,B与墙的底端C构成的三角形为直角三角形,
∴外心和与点C的距离始终为AB,
∴不发生变化,其长度为×8=4.
【知识点】三角形的外接圆与外心;直角三角形斜边上的中线
18.【答案】(1)
(2)
(3)内
【知识点】勾股定理;点与圆的位置关系;确定圆的条件
19.【答案】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
【知识点】确定圆的条件
20.【答案】(1);(2);(3)存在一个面积最小的,其最小值为平方米
【知识点】勾股定理;正方形的性质;三角形的外接圆与外心;解直角三角形
21世纪教育网(www.21cnjy.com)
2 / 7
3.5确定圆的条件
一、填空题
1.三角形三边垂直平分线的交点到三角形 的距离相等.
2.在一个直角三角形中,两边长分别是5,12,那么这个三角形的外接圆的半径是 .
3.若直角三角形的两直角边长为3、4,则该直角三角形的外接圆半径为 .
4.已知直角三角形的两条直角边长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离为 .
5.已知某直角三角形的边长分别是3cm、4cm,则它的外接圆半径是 cm.
6.如图所示,已知△ABC和△BDE都是等边三角形。下列结论:① AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥ FG∥AD。其中正确的有 个.
二、单选题
7.三角形的外心是( )
A.三条中线的交点 B.三个内角的角平分线的交点
C.三条边的垂直平分线的交点 D.三条高的交点
8.如图是由3个边长为2的正方形组成的物件,将它镶嵌在一个圆形的金属框上,使A,B,C三点恰好在金属框上,则该金属框的半径是( )
A. B. C. D.4
9.如图,将放在每个小正方形的边长为1的网格中,点、、均落在格点上,用一个圆面去覆盖,能够完全覆盖这个三角形的最小圆面的半径是( )
A. B. C.2 D.
10.下列说法正确的是( )
A.相等的角是对顶角
B.对角线相等的四边形是矩形
C.三角形的外心是它的三条角平分线的交点
D.线段垂直平分线上的点到线段两端的距离相等
11.过A,B,C三点能确定一个圆的条件是( )
①AB=2,BC=3,AC=5;②AB=3, BC=3,AC=2;③AB=3,BC=4,AC= 5.
A.①② B.①②③ C.②③ D.①③
12.如图,在由小正方形组成的网格中,点A,B,C,D,E,F,O均在格点上.下列三角形中,外心不是点O的是( )
A. B. C. D.
13.如图,在等腰△ABC中,AB=AC,把△ABC沿EF折叠,点C的对应点为O,连接AO,使AO平分∠BAC,若∠BAC=∠CFE=50°,则点O是( )
A.△ABC的内心 B.△ABC的外心 C.△ABF的内心 D.△ABF的外心
14.下列条件中,能确定一个圆的是( )
A.经过已知点M B.以点O为圆心,长为半径
C.以长为半径 D.以点O为圆心
15.如图, 中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA =3,则 外接圆的面积为( )
A. B. C. D.
16.已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
A.AC=BC+CD B. AC=BC+CD C. AC=BC+CD D.2AC=BC+CD
三、解答题
17.如图所示,在一个长度为8的梯子AB的顶点向点滑动的过程中,梯子的两端A,B与墙的底端构成的三角形的外心与点的距离是否发生变化 若发生变化,请说明理由;若不发生变化,请求出其长度.
18.如图,在平面直角坐标系中,A、B、C是上的三个点、、.
(1)写出圆心M的坐标为___________;
(2)这个圆的半径为___________;
(3)直接判断点与的位置关系.点在__________(填内、外、上).
19.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是
20.【问题提出】
(1)如图1,在边长为的等边中,点在边上,,连接,则的面积为____
【问题探究】
(2)如图2,已知在边长为的正方形中,点在边上,点在边上,且,若,求的面积;
【问题解决】
(3)如图3是我市华南大道的一部分,因自来水抢修,需要在米,米的矩形区域内开挖一个的工作面,其中、分别在、边上不与点、、重合,且,为了减少对该路段的交通拥堵影响,要求面积最小,那么是否存在一个面积最小的若存在,请求出面积的最小值;若不存在,请说明理由.
答案解析部分
1.【答案】三个顶点
【知识点】三角形的外接圆与外心
2.【答案】6或
【知识点】勾股定理;圆的相关概念;三角形的外接圆与外心;直角三角形斜边上的中线
3.【答案】
【知识点】勾股定理;三角形的外接圆与外心
4.【答案】
【知识点】勾股定理;三角形的外接圆与外心;三角形的重心及应用
5.【答案】2或2.5
【知识点】三角形的外接圆与外心
6.【答案】6
【知识点】全等三角形的判定与性质;等边三角形的判定与性质;圆周角定理;确定圆的条件
7.【答案】C
【知识点】三角形的外接圆与外心
8.【答案】A
【知识点】勾股定理;圆周角定理;确定圆的条件
9.【答案】D
【知识点】三角形的外接圆与外心
10.【答案】D
【知识点】线段垂直平分线的性质;矩形的判定;三角形的外接圆与外心;对顶角及其性质
11.【答案】C
【知识点】确定圆的条件
12.【答案】C
【知识点】三角形的外接圆与外心
13.【答案】B
【知识点】三角形的外接圆与外心
14.【答案】B
【知识点】确定圆的条件
15.【答案】D
【知识点】等腰三角形的性质;三角形的外接圆与外心
16.【答案】B
【知识点】全等三角形的判定与性质;三角形的外接圆与外心
17.【答案】解:不发生变化,理由如下:
∵梯子的两端A,B与墙的底端C构成的三角形为直角三角形,
∴外心和与点C的距离始终为AB,
∴不发生变化,其长度为×8=4.
【知识点】三角形的外接圆与外心;直角三角形斜边上的中线
18.【答案】(1)
(2)
(3)内
【知识点】勾股定理;点与圆的位置关系;确定圆的条件
19.【答案】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
【知识点】确定圆的条件
20.【答案】(1);(2);(3)存在一个面积最小的,其最小值为平方米
【知识点】勾股定理;正方形的性质;三角形的外接圆与外心;解直角三角形
21世纪教育网(www.21cnjy.com)
2 / 7
