北师大版数学九年级上册·下册综合复习题一 同步练习(含答案)
文档属性
| 名称 | 北师大版数学九年级上册·下册综合复习题一 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 599.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学九年级上册·下册综合复习题一
一、填空题
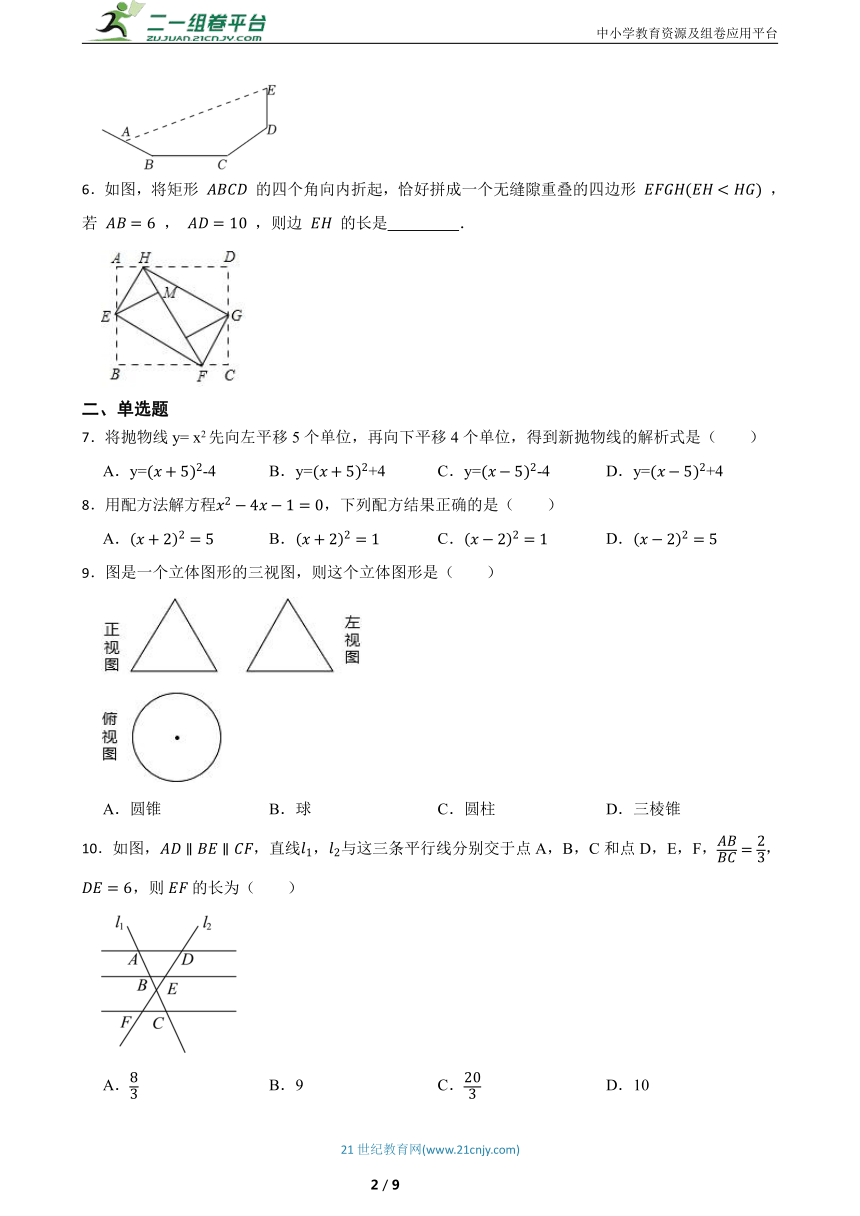
1.小灵为了测量操场边上一棵树的高度,她在树前方20米E点处放置一面小镜子,然后她沿方向继续往前走8米到D点处,转身刚好在镜子里看到树梢,小灵眼睛距地面米,根据这些信息请你算出树的高度是 米.
2.如图,P是反比例函数图象上的一点,轴于A,点B,C在y轴上,四边形PABC是平行四边形,则 PABC的面积是 .
3.已知(m-1)+3x-5=0是一元二次方程,则m= .
4.如图,为的直径,为半圆上一点且,,分别为,的中点,弦分别交,于点,.若,则 .
5.小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为30°的斜坡AB上的点A处,测得树尖E的仰角为15°,然后沿斜坡走了10米到达坡脚B处,又在水平路面上行走20米到达大树所在的斜坡坡脚C处,大树所在斜坡的坡度i=3:4,且大树的底端与坡脚的距离CD为15米,则大树ED的高度约为 .(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,.结果精确到0.1)
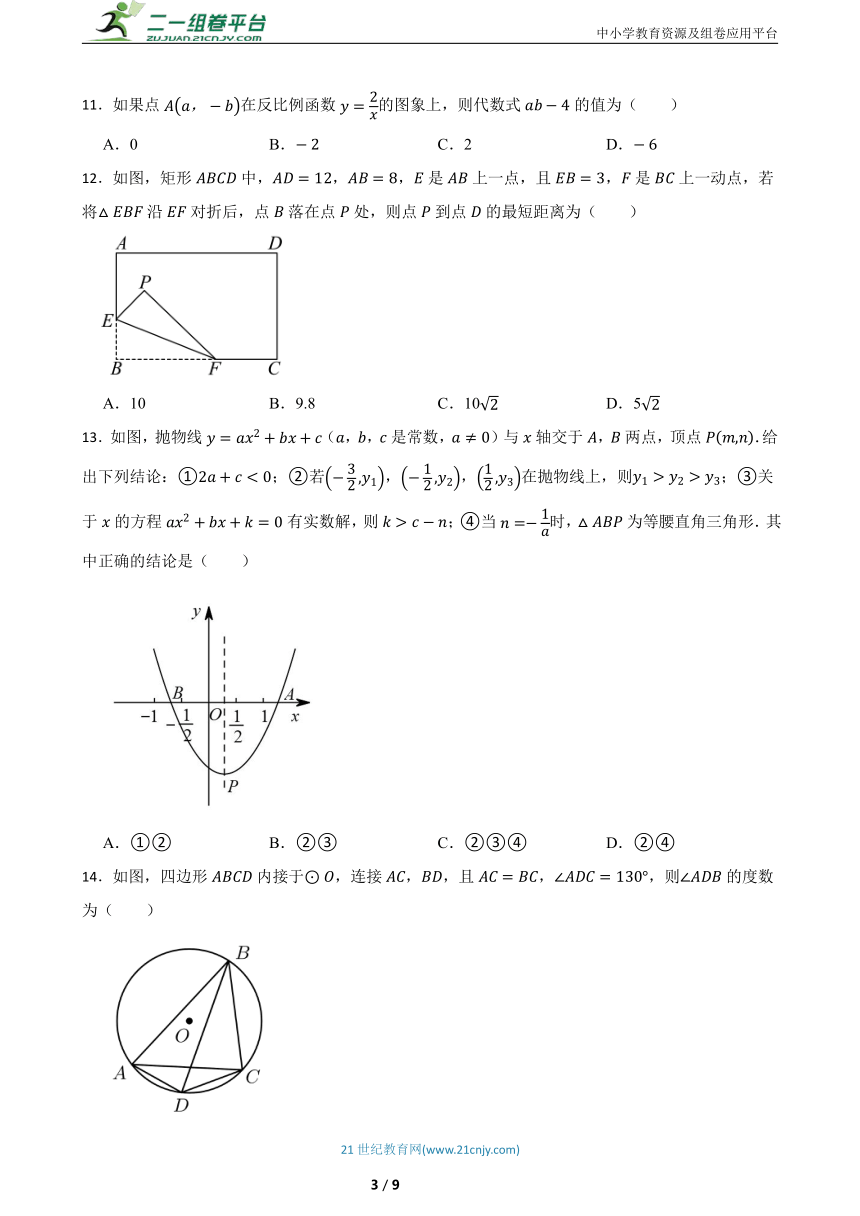
6.如图,将矩形 的四个角向内折起,恰好拼成一个无缝隙重叠的四边形 ,若 , ,则边 的长是 .
二、单选题
7.将抛物线y= x2先向左平移5个单位,再向下平移4个单位,得到新抛物线的解析式是( )
A.y=-4 B.y=+4 C.y=-4 D.y=+4
8.用配方法解方程,下列配方结果正确的是( )
A. B. C. D.
9.图是一个立体图形的三视图,则这个立体图形是( )
A.圆锥 B.球 C.圆柱 D.三棱锥
10.如图,,直线,与这三条平行线分别交于点A,B,C和点D,E,F,,,则的长为( )
A. B.9 C. D.10
11.如果点在反比例函数的图象上,则代数式的值为( )
A.0 B. C.2 D.
12.如图,矩形中,,,是上一点,且,是上一动点,若将沿对折后,点落在点处,则点到点的最短距离为( )
A.10 B.9.8 C.10 D.5
13.如图,抛物线(,,是常数,)与轴交于,两点,顶点.给出下列结论:①;②若,,在抛物线上,则;③关于的方程有实数解,则;④当时,为等腰直角三角形.其中正确的结论是( )
A.①② B.②③ C.②③④ D.②④
14.如图,四边形内接于,连接,,且,,则的度数为( )
A. B. C. D.
15.以关于的方程的两根的相反数为根的一元二次方程为( )
A. B. C. D.
16.如图,等边三角形的边长为,半圆的直径为1,连接,相交于点,将等边三角形从与重合的位置开始,绕点顺时针旋转().下列结论正确的是( )
结论Ⅰ:的长与的长之和为定值;结论Ⅱ:使得的值有两个;
结论Ⅲ:点运动的路径长为.
A.Ⅰ对Ⅱ对 B.Ⅱ错Ⅲ对 C.Ⅰ对Ⅲ错 D.Ⅰ错Ⅲ对
三、解答题
17.一个不透明的袋中装有分别标着汉字“温”“外”“数”“学”的4个小球,除汉字不同之外,小球材质、大小、形状全部相同,每次摸球前先搅拌均匀再摸球.
(1)求从袋中摸出一个球,则球上的汉字刚好是“温”的概率是________;
(2)从袋中任取一球,不放回,再从袋中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字恰能组成“数学”的概率.
18.小明参加某个“知书答理”竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项(分别表示为A,B,C),第二道单选题有4个选项(分别表示为a,b,c,d),这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
19.如图,反比例函数与一次函数的图象交于点、点.
(1)反比例函数为 ,一次函数为 ,不等式的解集为 ;
(2)点E为y轴上一个动点,若,求点E的坐标.
(3)若将一次函数的图像沿y轴向下平移n个单位,使平移后的图像与反比例函数的图像有且只有一个交点,则n的值是 .
20.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数的图像上,点D的坐标为(4,3),设AB所在直线解析式为.
(1)求反比例和一次函数解析式.
(2)若将菱形ABCD沿x轴正方向平移m个单位,在平移中若反比例函数图象与菱形的边AD始终有交点,求m的取值范围.
(3)在直线AB上是否存在M、N两点,使以MNOD四点的四边形构成矩形?若不存在,请说明理由,若存在直接求出M、N(点M在点N的上方)两点的坐标.
四、计算题
21.计算:.
22.
(1)分解因式:3a2﹣6a+3;
(2)解方程:x2﹣4x+2=0.
23.如图,在某中学的一场篮球赛中,小明在距离篮圈中心7.3m(水平距离)远处跳起投篮,已知球出手时离地面,当篮球运行的水平距离为4m时达到离地面的最大高度4m.已知篮球在空中的运行路线为一条抛物线,篮圈中心距地面3m.
(1)建立如图的平面直角坐标系,求篮球运行路线所在抛物线的函数表达式;
(2)场边看球的小丽认为:小明投出的此球不能命中篮圈中心.
①请通过计算说明小丽判断的正确性;
②若球出手的角度和力度都不变,小明应该向前走或向后退多少米才能命中篮圈中心?
(3)在球出手后,未达到最高点时,被防守队员拦截下来称为盖帽,但球到达最高点后,处于下落过程时,防守队员再出手拦截,属于犯规.在(1)的条件下,防守方球员小亮前来盖帽,已知小亮的最大摸球高度为3.19m,则他应在小明前面多少米范围处跳起拦截才能盖帽成功?
答案解析部分
1.【答案】
【知识点】相似三角形的应用
2.【答案】6
【知识点】反比例函数系数k的几何意义
3.【答案】-1
【知识点】一元二次方程的定义及相关的量
4.【答案】15
【知识点】勾股定理;垂径定理;圆周角定理;解直角三角形
5.【答案】7.0米
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣坡度坡角问题
6.【答案】
【知识点】矩形的性质;翻折变换(折叠问题)
7.【答案】A
【知识点】二次函数图象的几何变换
8.【答案】D
【知识点】配方法的应用
9.【答案】A
【知识点】由三视图判断几何体
10.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】D
【知识点】反比例函数的概念
12.【答案】A
【知识点】三角形三边关系;勾股定理;矩形的性质
13.【答案】D
【知识点】二次函数图象与系数的关系;等腰三角形的判定与性质
14.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
15.【答案】A
【知识点】一元二次方程的根;一元二次方程的根与系数的关系(韦达定理)
16.【答案】B
【知识点】圆周角定理;圆内接四边形的性质;弧长的计算;解直角三角形
17.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
18.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
19.【答案】(1),,不等式的解集为或
(2)点E的坐标为或
(3)
【知识点】一元二次方程根的判别式及应用;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
20.【答案】(1),
(2)0≤m≤
(3)点N坐标为(,);点M的坐标为(,)
【知识点】待定系数法求一次函数解析式;菱形的性质;矩形的性质
21.【答案】
【知识点】零指数幂;求特殊角的三角函数值;开立方(求立方根)
22.【答案】(1)解:3a2﹣6a+3
=3(a2-2a+1)
=3(a-1)2;
(2)解:x2-4x+2=0,
x2-4x=-2,
x2-4x+4=2
(x-2)2=2,
x-2=±,
所以x1=2+,x2=2-.
【知识点】因式分解﹣综合运用提公因式与公式法;配方法解一元二次方程
23.【答案】(1)
(2)①小丽的判断是正确的;②小明应向前走0.3m才能命中篮圈中心
(3)1.3米
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式;通过函数图象获取信息;二次函数的实际应用-抛球问题
21世纪教育网(www.21cnjy.com)
2 / 9
北师大版数学九年级上册·下册综合复习题一
一、填空题
1.小灵为了测量操场边上一棵树的高度,她在树前方20米E点处放置一面小镜子,然后她沿方向继续往前走8米到D点处,转身刚好在镜子里看到树梢,小灵眼睛距地面米,根据这些信息请你算出树的高度是 米.
2.如图,P是反比例函数图象上的一点,轴于A,点B,C在y轴上,四边形PABC是平行四边形,则 PABC的面积是 .
3.已知(m-1)+3x-5=0是一元二次方程,则m= .
4.如图,为的直径,为半圆上一点且,,分别为,的中点,弦分别交,于点,.若,则 .
5.小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为30°的斜坡AB上的点A处,测得树尖E的仰角为15°,然后沿斜坡走了10米到达坡脚B处,又在水平路面上行走20米到达大树所在的斜坡坡脚C处,大树所在斜坡的坡度i=3:4,且大树的底端与坡脚的距离CD为15米,则大树ED的高度约为 .(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,.结果精确到0.1)
6.如图,将矩形 的四个角向内折起,恰好拼成一个无缝隙重叠的四边形 ,若 , ,则边 的长是 .
二、单选题
7.将抛物线y= x2先向左平移5个单位,再向下平移4个单位,得到新抛物线的解析式是( )
A.y=-4 B.y=+4 C.y=-4 D.y=+4
8.用配方法解方程,下列配方结果正确的是( )
A. B. C. D.
9.图是一个立体图形的三视图,则这个立体图形是( )
A.圆锥 B.球 C.圆柱 D.三棱锥
10.如图,,直线,与这三条平行线分别交于点A,B,C和点D,E,F,,,则的长为( )
A. B.9 C. D.10
11.如果点在反比例函数的图象上,则代数式的值为( )
A.0 B. C.2 D.
12.如图,矩形中,,,是上一点,且,是上一动点,若将沿对折后,点落在点处,则点到点的最短距离为( )
A.10 B.9.8 C.10 D.5
13.如图,抛物线(,,是常数,)与轴交于,两点,顶点.给出下列结论:①;②若,,在抛物线上,则;③关于的方程有实数解,则;④当时,为等腰直角三角形.其中正确的结论是( )
A.①② B.②③ C.②③④ D.②④
14.如图,四边形内接于,连接,,且,,则的度数为( )
A. B. C. D.
15.以关于的方程的两根的相反数为根的一元二次方程为( )
A. B. C. D.
16.如图,等边三角形的边长为,半圆的直径为1,连接,相交于点,将等边三角形从与重合的位置开始,绕点顺时针旋转().下列结论正确的是( )
结论Ⅰ:的长与的长之和为定值;结论Ⅱ:使得的值有两个;
结论Ⅲ:点运动的路径长为.
A.Ⅰ对Ⅱ对 B.Ⅱ错Ⅲ对 C.Ⅰ对Ⅲ错 D.Ⅰ错Ⅲ对
三、解答题
17.一个不透明的袋中装有分别标着汉字“温”“外”“数”“学”的4个小球,除汉字不同之外,小球材质、大小、形状全部相同,每次摸球前先搅拌均匀再摸球.
(1)求从袋中摸出一个球,则球上的汉字刚好是“温”的概率是________;
(2)从袋中任取一球,不放回,再从袋中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字恰能组成“数学”的概率.
18.小明参加某个“知书答理”竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项(分别表示为A,B,C),第二道单选题有4个选项(分别表示为a,b,c,d),这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
19.如图,反比例函数与一次函数的图象交于点、点.
(1)反比例函数为 ,一次函数为 ,不等式的解集为 ;
(2)点E为y轴上一个动点,若,求点E的坐标.
(3)若将一次函数的图像沿y轴向下平移n个单位,使平移后的图像与反比例函数的图像有且只有一个交点,则n的值是 .
20.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数的图像上,点D的坐标为(4,3),设AB所在直线解析式为.
(1)求反比例和一次函数解析式.
(2)若将菱形ABCD沿x轴正方向平移m个单位,在平移中若反比例函数图象与菱形的边AD始终有交点,求m的取值范围.
(3)在直线AB上是否存在M、N两点,使以MNOD四点的四边形构成矩形?若不存在,请说明理由,若存在直接求出M、N(点M在点N的上方)两点的坐标.
四、计算题
21.计算:.
22.
(1)分解因式:3a2﹣6a+3;
(2)解方程:x2﹣4x+2=0.
23.如图,在某中学的一场篮球赛中,小明在距离篮圈中心7.3m(水平距离)远处跳起投篮,已知球出手时离地面,当篮球运行的水平距离为4m时达到离地面的最大高度4m.已知篮球在空中的运行路线为一条抛物线,篮圈中心距地面3m.
(1)建立如图的平面直角坐标系,求篮球运行路线所在抛物线的函数表达式;
(2)场边看球的小丽认为:小明投出的此球不能命中篮圈中心.
①请通过计算说明小丽判断的正确性;
②若球出手的角度和力度都不变,小明应该向前走或向后退多少米才能命中篮圈中心?
(3)在球出手后,未达到最高点时,被防守队员拦截下来称为盖帽,但球到达最高点后,处于下落过程时,防守队员再出手拦截,属于犯规.在(1)的条件下,防守方球员小亮前来盖帽,已知小亮的最大摸球高度为3.19m,则他应在小明前面多少米范围处跳起拦截才能盖帽成功?
答案解析部分
1.【答案】
【知识点】相似三角形的应用
2.【答案】6
【知识点】反比例函数系数k的几何意义
3.【答案】-1
【知识点】一元二次方程的定义及相关的量
4.【答案】15
【知识点】勾股定理;垂径定理;圆周角定理;解直角三角形
5.【答案】7.0米
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣坡度坡角问题
6.【答案】
【知识点】矩形的性质;翻折变换(折叠问题)
7.【答案】A
【知识点】二次函数图象的几何变换
8.【答案】D
【知识点】配方法的应用
9.【答案】A
【知识点】由三视图判断几何体
10.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】D
【知识点】反比例函数的概念
12.【答案】A
【知识点】三角形三边关系;勾股定理;矩形的性质
13.【答案】D
【知识点】二次函数图象与系数的关系;等腰三角形的判定与性质
14.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
15.【答案】A
【知识点】一元二次方程的根;一元二次方程的根与系数的关系(韦达定理)
16.【答案】B
【知识点】圆周角定理;圆内接四边形的性质;弧长的计算;解直角三角形
17.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
18.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
19.【答案】(1),,不等式的解集为或
(2)点E的坐标为或
(3)
【知识点】一元二次方程根的判别式及应用;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
20.【答案】(1),
(2)0≤m≤
(3)点N坐标为(,);点M的坐标为(,)
【知识点】待定系数法求一次函数解析式;菱形的性质;矩形的性质
21.【答案】
【知识点】零指数幂;求特殊角的三角函数值;开立方(求立方根)
22.【答案】(1)解:3a2﹣6a+3
=3(a2-2a+1)
=3(a-1)2;
(2)解:x2-4x+2=0,
x2-4x=-2,
x2-4x+4=2
(x-2)2=2,
x-2=±,
所以x1=2+,x2=2-.
【知识点】因式分解﹣综合运用提公因式与公式法;配方法解一元二次方程
23.【答案】(1)
(2)①小丽的判断是正确的;②小明应向前走0.3m才能命中篮圈中心
(3)1.3米
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式;通过函数图象获取信息;二次函数的实际应用-抛球问题
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
