北师大版数学九年级上册·下册综合题二 同步练习(含答案)
文档属性
| 名称 | 北师大版数学九年级上册·下册综合题二 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 592.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学九年级上册·下册综合题二
一、填空题
1.写出一个二次函数,使其图象满足:①开口向下;②与y轴交于点(0, 2),这个二次函数的解析式可以是 .
2.反比例函数经过点,则 .
3.如图,是的直径,,是上的点,若的半径为,,则的长为 .
4.若是关于x的一元二次方程的一个解,则 .
5.如图,中,A、B两个顶点在x轴的上方,点C的坐标是 ,以点C为位似中心,在x轴的下方作中的位似图形,并把中的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是 .
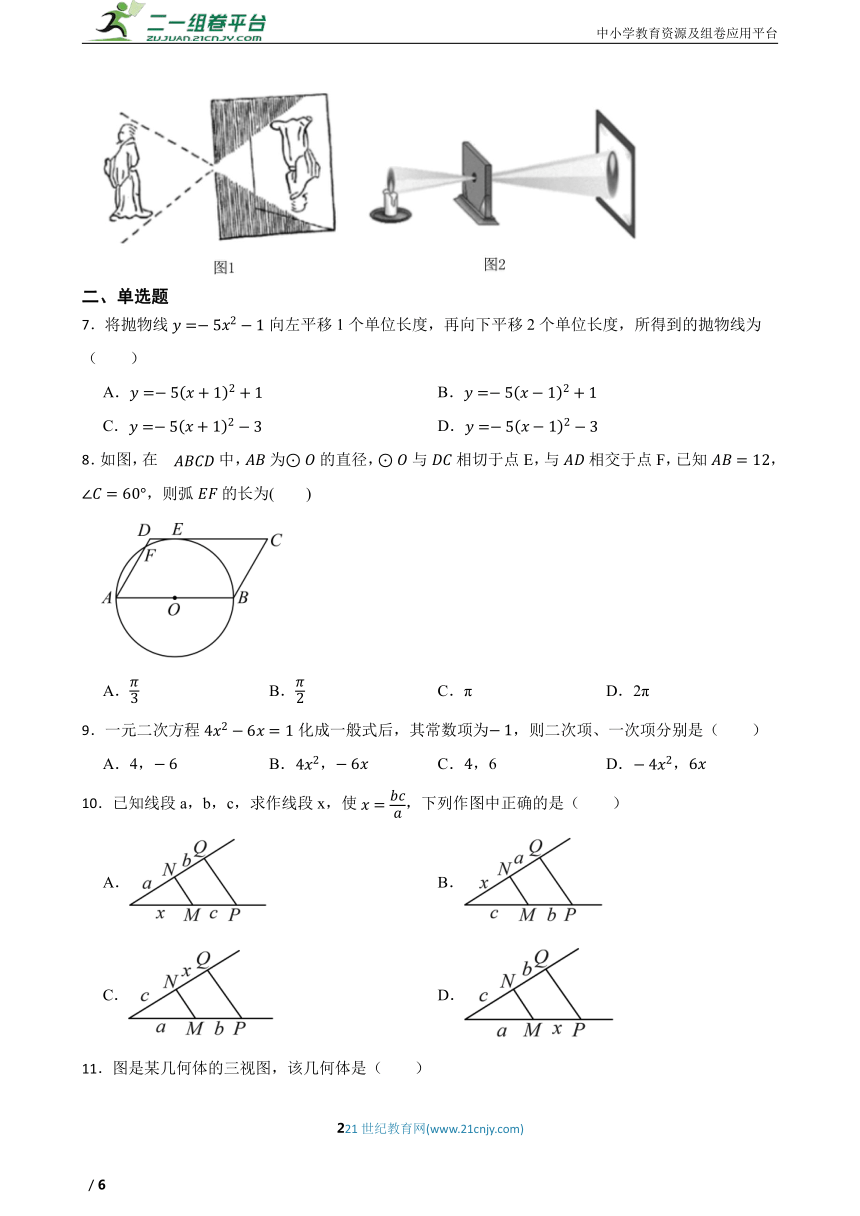
6.大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”,如图2所示的小孔成像实验中,若物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是 .
二、单选题
7.将抛物线向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A. B.
C. D.
8.如图,在中,为的直径,与相切于点E,与相交于点F,已知,,则弧的长为( )
A. B. C.π D.2π
9.一元二次方程化成一般式后,其常数项为,则二次项、一次项分别是( )
A.4, B., C.,6 D.,
10.已知线段a,b,c,求作线段x,使,下列作图中正确的是( )
A. B.
C. D.
11.图是某几何体的三视图,该几何体是( )
A.三棱锥 B.三棱柱 C.圆柱 D.长方体
三、判断题
12.圆的周长是直径的 π 倍.(判断对错)
13.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
四、解答题
14.已知二次函数的图象与x轴交于.
(1)求二次函数的解析式;
(2)当时,求自变量x的值.
15.正方形的边长为4,当边长增加x时,面积增加y,求y与x之间的函数关系式.
五、计算题
16.计算:.
17.解方程:
(1);
(2).
六、综合题
18.如图是甲、乙两人进行羽毛球比赛时的一个瞬间,羽毛球飞行的高度y(m)与水平距离x(m)的路线为抛物线的一部分.甲在点O正上方1m的P处发出一球,已知点O与球网的水平距离为5m,球网的高度为.当羽毛球在水平方向上运动4m时,达到最大高度2m.
(1)求羽毛球经过的路线对应的函数表达式.
(2)通过计算判断此球能否过网.
(3)若甲发球过网后,羽毛球飞行到离地面的高度为m的Q处时,乙击球成功,求此时乙与球网的水平距离.
19.如图,要利用一面墙(墙长为)建羊圈(矩形,用的围栏围成总面积为的三个大小相同的矩形羊圈,求羊圈的边长的长度.
20.某超市购进了一批水果,进货价格为每箱50元,若按每箱60元出售,则每天可销售80箱,现准备提价销售,经市场调研发现:每箱每提价1元,每天的销量就会减少2箱,为保护消费者利益,物价部门规定销售利润不能超过,设该水果售价为每箱元.
(1)用含x的代数式表示提价后平均每天的销量为________箱;
(2)若超市销售该水果每天想要获得1200元的利润,则应按每箱多少元销售?
七、实践探究题
21.2022年6月6日是第27个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.如图,当张角时,顶部边缘处离桌面的高度的长为,此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角时(点是的对应点),用眼舒适度较为理想.求此时顶部边缘处离桌面的高度的长.(结果精确到;参考数据:,,)
答案解析部分
1.【答案】
【知识点】待定系数法求二次函数解析式
2.【答案】
【知识点】待定系数法求反比例函数解析式
3.【答案】
【知识点】圆周角定理;弧长的计算
4.【答案】1
【知识点】一元二次方程的根
5.【答案】
【知识点】坐标与图形变化﹣位似
6.【答案】4
【知识点】相似三角形的性质
7.【答案】C
【知识点】二次函数图象的几何变换
8.【答案】C
【知识点】平行四边形的性质;切线的性质;弧长的计算
9.【答案】B
【知识点】一元二次方程的定义及相关的量
10.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】B
【知识点】由三视图判断几何体
12.【答案】正确
【知识点】圆的相关概念
13.【答案】(1)正确
(2)错误
【知识点】垂径定理
14.【答案】(1);
(2)当时,自变量的值为或6
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
15.【答案】
【知识点】二次函数的实际应用-几何问题
16.【答案】
【知识点】负整数指数幂;二次根式的混合运算;求特殊角的三角函数值
17.【答案】(1)解:,
,
解得:
(2)解:,
,
,
,
,
解得:
【知识点】配方法解一元二次方程;公式法解一元二次方程
18.【答案】(1)y=
(2)能
(3)2米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
19.【答案】
【知识点】一元二次方程的应用-几何问题
20.【答案】(1);
(2)70元.
【知识点】一元二次方程的实际应用-销售问题
21.【答案】约为
【知识点】解直角三角形的其他实际应用
2
21世纪教育网(www.21cnjy.com)
/ 6
北师大版数学九年级上册·下册综合题二
一、填空题
1.写出一个二次函数,使其图象满足:①开口向下;②与y轴交于点(0, 2),这个二次函数的解析式可以是 .
2.反比例函数经过点,则 .
3.如图,是的直径,,是上的点,若的半径为,,则的长为 .
4.若是关于x的一元二次方程的一个解,则 .
5.如图,中,A、B两个顶点在x轴的上方,点C的坐标是 ,以点C为位似中心,在x轴的下方作中的位似图形,并把中的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是 .
6.大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”,如图2所示的小孔成像实验中,若物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是 .
二、单选题
7.将抛物线向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A. B.
C. D.
8.如图,在中,为的直径,与相切于点E,与相交于点F,已知,,则弧的长为( )
A. B. C.π D.2π
9.一元二次方程化成一般式后,其常数项为,则二次项、一次项分别是( )
A.4, B., C.,6 D.,
10.已知线段a,b,c,求作线段x,使,下列作图中正确的是( )
A. B.
C. D.
11.图是某几何体的三视图,该几何体是( )
A.三棱锥 B.三棱柱 C.圆柱 D.长方体
三、判断题
12.圆的周长是直径的 π 倍.(判断对错)
13.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
四、解答题
14.已知二次函数的图象与x轴交于.
(1)求二次函数的解析式;
(2)当时,求自变量x的值.
15.正方形的边长为4,当边长增加x时,面积增加y,求y与x之间的函数关系式.
五、计算题
16.计算:.
17.解方程:
(1);
(2).
六、综合题
18.如图是甲、乙两人进行羽毛球比赛时的一个瞬间,羽毛球飞行的高度y(m)与水平距离x(m)的路线为抛物线的一部分.甲在点O正上方1m的P处发出一球,已知点O与球网的水平距离为5m,球网的高度为.当羽毛球在水平方向上运动4m时,达到最大高度2m.
(1)求羽毛球经过的路线对应的函数表达式.
(2)通过计算判断此球能否过网.
(3)若甲发球过网后,羽毛球飞行到离地面的高度为m的Q处时,乙击球成功,求此时乙与球网的水平距离.
19.如图,要利用一面墙(墙长为)建羊圈(矩形,用的围栏围成总面积为的三个大小相同的矩形羊圈,求羊圈的边长的长度.
20.某超市购进了一批水果,进货价格为每箱50元,若按每箱60元出售,则每天可销售80箱,现准备提价销售,经市场调研发现:每箱每提价1元,每天的销量就会减少2箱,为保护消费者利益,物价部门规定销售利润不能超过,设该水果售价为每箱元.
(1)用含x的代数式表示提价后平均每天的销量为________箱;
(2)若超市销售该水果每天想要获得1200元的利润,则应按每箱多少元销售?
七、实践探究题
21.2022年6月6日是第27个全国“爱眼日”,某数学兴趣小组开展了“笔记本电脑的张角大小、顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动.如图,当张角时,顶部边缘处离桌面的高度的长为,此时用眼舒适度不太理想.小组成员调整张角大小继续探究,最后联系黄金比知识,发现当张角时(点是的对应点),用眼舒适度较为理想.求此时顶部边缘处离桌面的高度的长.(结果精确到;参考数据:,,)
答案解析部分
1.【答案】
【知识点】待定系数法求二次函数解析式
2.【答案】
【知识点】待定系数法求反比例函数解析式
3.【答案】
【知识点】圆周角定理;弧长的计算
4.【答案】1
【知识点】一元二次方程的根
5.【答案】
【知识点】坐标与图形变化﹣位似
6.【答案】4
【知识点】相似三角形的性质
7.【答案】C
【知识点】二次函数图象的几何变换
8.【答案】C
【知识点】平行四边形的性质;切线的性质;弧长的计算
9.【答案】B
【知识点】一元二次方程的定义及相关的量
10.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】B
【知识点】由三视图判断几何体
12.【答案】正确
【知识点】圆的相关概念
13.【答案】(1)正确
(2)错误
【知识点】垂径定理
14.【答案】(1);
(2)当时,自变量的值为或6
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
15.【答案】
【知识点】二次函数的实际应用-几何问题
16.【答案】
【知识点】负整数指数幂;二次根式的混合运算;求特殊角的三角函数值
17.【答案】(1)解:,
,
解得:
(2)解:,
,
,
,
,
解得:
【知识点】配方法解一元二次方程;公式法解一元二次方程
18.【答案】(1)y=
(2)能
(3)2米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
19.【答案】
【知识点】一元二次方程的应用-几何问题
20.【答案】(1);
(2)70元.
【知识点】一元二次方程的实际应用-销售问题
21.【答案】约为
【知识点】解直角三角形的其他实际应用
2
21世纪教育网(www.21cnjy.com)
/ 6
同课章节目录
