2.5.1 直线与圆的位置关系 课时作业(含答案)2024-2025学年数学湘教版九年级下册
文档属性
| 名称 | 2.5.1 直线与圆的位置关系 课时作业(含答案)2024-2025学年数学湘教版九年级下册 | 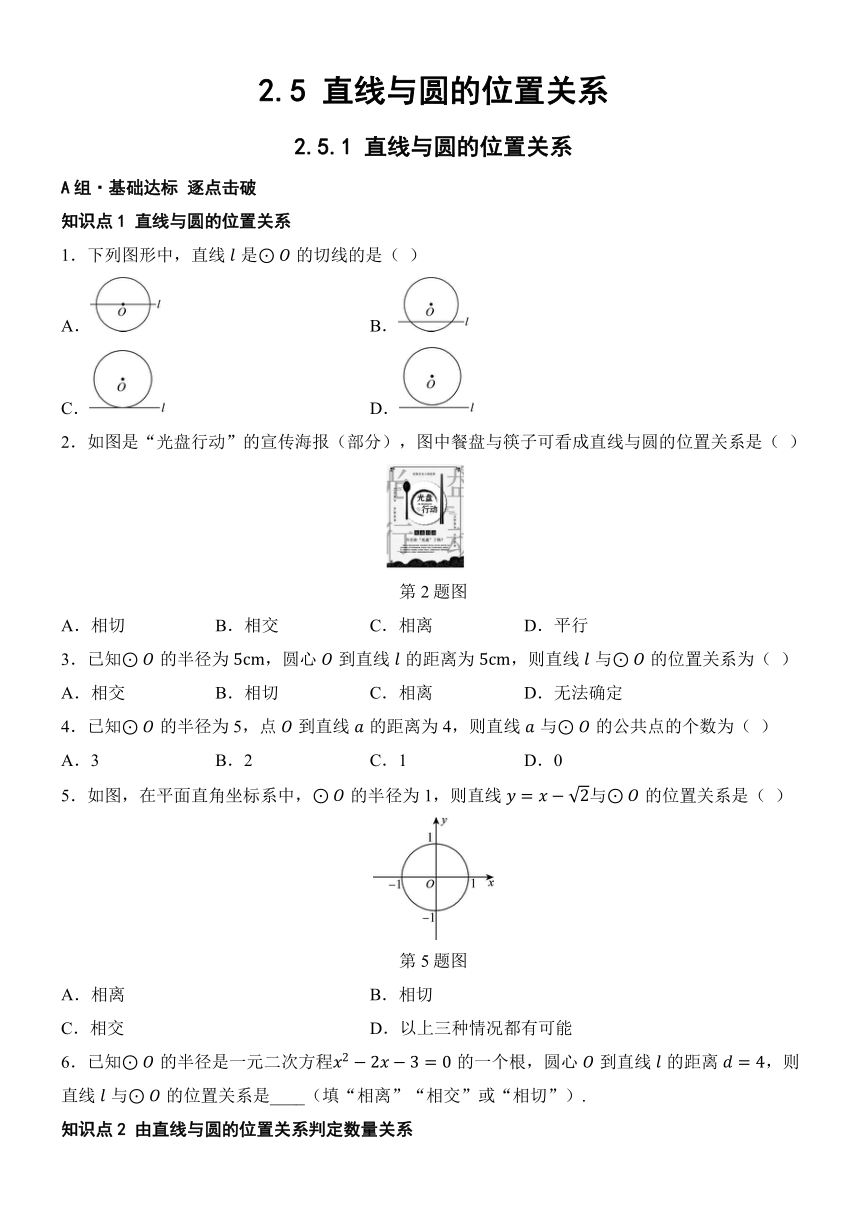 | |
| 格式 | docx | ||
| 文件大小 | 156.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 21:35:34 | ||
图片预览



文档简介
2.5 直线与圆的位置关系
2.5.1 直线与圆的位置关系
A组·基础达标 逐点击破
知识点1 直线与圆的位置关系
1.下列图形中,直线是的切线的是( )
A. B.
C. D.
2.如图是“光盘行动”的宣传海报(部分),图中餐盘与筷子可看成直线与圆的位置关系是( )
第2题图
A.相切 B.相交 C.相离 D.平行
3.已知的半径为,圆心到直线的距离为,则直线与的位置关系为( )
A.相交 B.相切 C.相离 D.无法确定
4.已知的半径为5,点到直线的距离为4,则直线与的公共点的个数为( )
A.3 B.2 C.1 D.0
5.如图,在平面直角坐标系中,的半径为1,则直线与的位置关系是( )
第5题图
A.相离 B.相切
C.相交 D.以上三种情况都有可能
6.已知的半径是一元二次方程的一个根,圆心到直线的距离,则直线与的位置关系是____(填“相离”“相交”或“相切”).
知识点2 由直线与圆的位置关系判定数量关系
7.在平面直角坐标系中,如果以点为圆心、以为半径作与轴相交,且原点在的外部,那么半径的取值范围是( )
A. B. C. D.
8.[2023衡阳]如图,在中, ,,.以点为圆心,为半径作圆,当所作的圆与斜边所在的直线相切时,的值为________.
易错点 直线与圆的位置关系未考虑全面而漏解
9.已知平面内有和两点,,若的半径为,线段,,则直线与的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
B组·能力提升 强化突破
10.如图,已知,是边上一点,以点为圆心,为半径作.当时,与直线的位置关系是( )
第10题图
A.相离 B.相交 C.相切 D.无法确定
11.[2024益阳模拟]如图,在平面直角坐标系中,半径为2的的圆心的坐标为,将沿轴正方向平移,使与轴相切,则平移的距离为( )
第11题图
A.1 B.1或5 C.3 D.5
12.如图,在平面直角坐标系中,与轴交于,两点,点的坐标为,.
(1) 求的半径;
(2) 将向下平移,求与轴相切时平移的距离.
13.在中,,,.
(1) 若以点为圆心,长为半径画,求直线与的位置关系;
(2) 若直线与半径为的相切,求的值;
(3) 若线段与半径为的有唯一公共点,求的取值范围.
14.已知 ,点在上,以点为圆心,2为半径作,交于点,,设.
(1) 如图①,当取何值时,直线与相切?
(2) 如图②,当取何值时,直线交于点,,且 ?
C组·核心素养拓展 素养渗透
15.【几何直观,空间观念】在平面直角坐标系中,的圆心在轴上,半径为1,沿轴向右平移.
(1) 如图①,当与轴相切时,点的坐标为____________________________;
(2) 如图②,设以每秒1个单位的速度从原点沿轴向右平移,直线与轴交于点,与轴交于点.问:在运动过程中与直线有公共点的时间共几秒?
2.5 直线与圆的位置关系
2.5.1 直线与圆的位置关系
课堂导学
知识梳理
; ; ; 切点; 切线
例题引路
【思路分析】判断与直线的位置关系,只需先求出圆心到直线的距离,然后与比较大小即可.
例 (1) 【规范解答】如答图,过点 作 于点.
例题答图
在 中, ,
,,则.
,
,
即,.
例 (1) 当 时,,与直线 相离.
(2) 当 时,,与直线 相切.
(3) 当 时,,与直线 相交.
A组·基础达标 逐点击破
知识点1 直线与圆的位置关系
1.C 2.B 3.B 4.B 5.B
6.相离
知识点2 由直线与圆的位置关系判定数量关系
7.C
8.
易错点 直线与圆的位置关系未考虑全面而漏解
9.D
B组·能力提升 强化突破
10.C 11.B
12.(1) 解:如答图,连接,过点作于点.
第12题答图
由垂径定理,得
.
在中,由勾股定理,得
,
.
的半径为2.
(2) 将向下平移,当与轴相切时,点到轴的距离等于半径,
平移的距离为.
13.(1) 解:,,,
.
是直角三角形,且 .
作于点.
由的面积,得,
若以点为圆心,长为半径画,则直线与的位置关系是相离.
(2) 由(1)知于点,,
当时,直线与半径为的相切.
(3) 若线段与半径为的有唯一公共点,分两种情况:
①与相切时,即;
②点在内部,点在上或外部时,.
的取值范围是或.
14.(1) 解:如答图①,过点作,垂足为,
第14题答图①
当时,
与直线相切, ,
,
故.即当时,直线与相切.
(2) 如答图②,过点作,垂足为.则.
第14题答图②
, ,
.
..
,.
,即当时,直线交于点,,且 .
C组·核心素养拓展 素养渗透
15.(1) 或
[解析]已知的半径为1,
故当在轴左侧与轴相切时,点的坐标为,
当在轴右侧与轴相切时,点的坐标为,
即当与轴相切时,点的坐标为或.
(2) 解:与轴、轴分别交于点,,
,,
,,.
设经过后与直线相切,过点作于点(图略),则.
①当在直线的左边与直线相切时,,
,,
即,解得;
②当在直线的右边与直线相切时,.
,,
即,
解得.
.
在运动过程中,与直线有公共点的时间共有.
2.5.1 直线与圆的位置关系
A组·基础达标 逐点击破
知识点1 直线与圆的位置关系
1.下列图形中,直线是的切线的是( )
A. B.
C. D.
2.如图是“光盘行动”的宣传海报(部分),图中餐盘与筷子可看成直线与圆的位置关系是( )
第2题图
A.相切 B.相交 C.相离 D.平行
3.已知的半径为,圆心到直线的距离为,则直线与的位置关系为( )
A.相交 B.相切 C.相离 D.无法确定
4.已知的半径为5,点到直线的距离为4,则直线与的公共点的个数为( )
A.3 B.2 C.1 D.0
5.如图,在平面直角坐标系中,的半径为1,则直线与的位置关系是( )
第5题图
A.相离 B.相切
C.相交 D.以上三种情况都有可能
6.已知的半径是一元二次方程的一个根,圆心到直线的距离,则直线与的位置关系是____(填“相离”“相交”或“相切”).
知识点2 由直线与圆的位置关系判定数量关系
7.在平面直角坐标系中,如果以点为圆心、以为半径作与轴相交,且原点在的外部,那么半径的取值范围是( )
A. B. C. D.
8.[2023衡阳]如图,在中, ,,.以点为圆心,为半径作圆,当所作的圆与斜边所在的直线相切时,的值为________.
易错点 直线与圆的位置关系未考虑全面而漏解
9.已知平面内有和两点,,若的半径为,线段,,则直线与的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
B组·能力提升 强化突破
10.如图,已知,是边上一点,以点为圆心,为半径作.当时,与直线的位置关系是( )
第10题图
A.相离 B.相交 C.相切 D.无法确定
11.[2024益阳模拟]如图,在平面直角坐标系中,半径为2的的圆心的坐标为,将沿轴正方向平移,使与轴相切,则平移的距离为( )
第11题图
A.1 B.1或5 C.3 D.5
12.如图,在平面直角坐标系中,与轴交于,两点,点的坐标为,.
(1) 求的半径;
(2) 将向下平移,求与轴相切时平移的距离.
13.在中,,,.
(1) 若以点为圆心,长为半径画,求直线与的位置关系;
(2) 若直线与半径为的相切,求的值;
(3) 若线段与半径为的有唯一公共点,求的取值范围.
14.已知 ,点在上,以点为圆心,2为半径作,交于点,,设.
(1) 如图①,当取何值时,直线与相切?
(2) 如图②,当取何值时,直线交于点,,且 ?
C组·核心素养拓展 素养渗透
15.【几何直观,空间观念】在平面直角坐标系中,的圆心在轴上,半径为1,沿轴向右平移.
(1) 如图①,当与轴相切时,点的坐标为____________________________;
(2) 如图②,设以每秒1个单位的速度从原点沿轴向右平移,直线与轴交于点,与轴交于点.问:在运动过程中与直线有公共点的时间共几秒?
2.5 直线与圆的位置关系
2.5.1 直线与圆的位置关系
课堂导学
知识梳理
; ; ; 切点; 切线
例题引路
【思路分析】判断与直线的位置关系,只需先求出圆心到直线的距离,然后与比较大小即可.
例 (1) 【规范解答】如答图,过点 作 于点.
例题答图
在 中, ,
,,则.
,
,
即,.
例 (1) 当 时,,与直线 相离.
(2) 当 时,,与直线 相切.
(3) 当 时,,与直线 相交.
A组·基础达标 逐点击破
知识点1 直线与圆的位置关系
1.C 2.B 3.B 4.B 5.B
6.相离
知识点2 由直线与圆的位置关系判定数量关系
7.C
8.
易错点 直线与圆的位置关系未考虑全面而漏解
9.D
B组·能力提升 强化突破
10.C 11.B
12.(1) 解:如答图,连接,过点作于点.
第12题答图
由垂径定理,得
.
在中,由勾股定理,得
,
.
的半径为2.
(2) 将向下平移,当与轴相切时,点到轴的距离等于半径,
平移的距离为.
13.(1) 解:,,,
.
是直角三角形,且 .
作于点.
由的面积,得,
若以点为圆心,长为半径画,则直线与的位置关系是相离.
(2) 由(1)知于点,,
当时,直线与半径为的相切.
(3) 若线段与半径为的有唯一公共点,分两种情况:
①与相切时,即;
②点在内部,点在上或外部时,.
的取值范围是或.
14.(1) 解:如答图①,过点作,垂足为,
第14题答图①
当时,
与直线相切, ,
,
故.即当时,直线与相切.
(2) 如答图②,过点作,垂足为.则.
第14题答图②
, ,
.
..
,.
,即当时,直线交于点,,且 .
C组·核心素养拓展 素养渗透
15.(1) 或
[解析]已知的半径为1,
故当在轴左侧与轴相切时,点的坐标为,
当在轴右侧与轴相切时,点的坐标为,
即当与轴相切时,点的坐标为或.
(2) 解:与轴、轴分别交于点,,
,,
,,.
设经过后与直线相切,过点作于点(图略),则.
①当在直线的左边与直线相切时,,
,,
即,解得;
②当在直线的右边与直线相切时,.
,,
即,
解得.
.
在运动过程中,与直线有公共点的时间共有.
