2.5.3 切线长定理 课时作业(含答案)2024-2025学年数学湘教版九年级下册
文档属性
| 名称 | 2.5.3 切线长定理 课时作业(含答案)2024-2025学年数学湘教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 111.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 21:38:03 | ||
图片预览


文档简介
*2.5.3 切线长定理
A组·基础达标 逐点击破
知识点 切线长定理
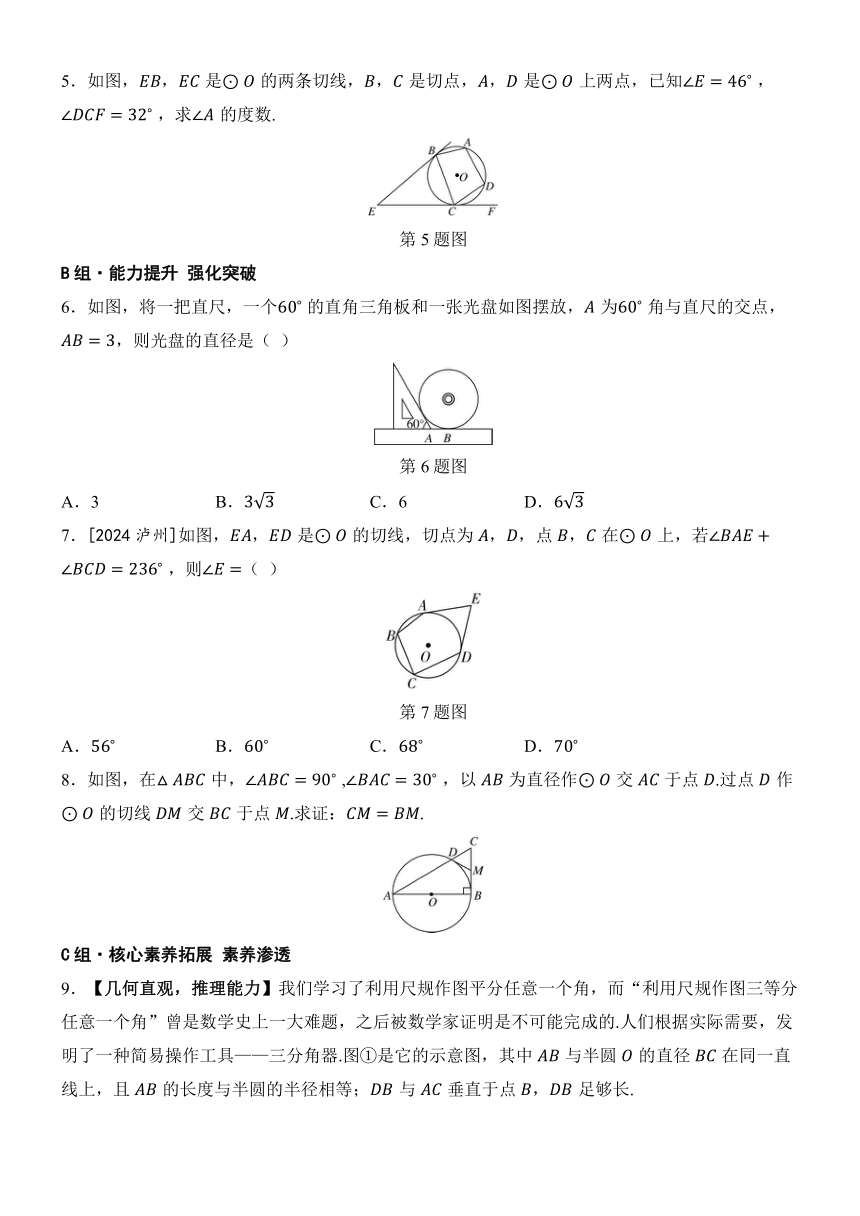
1.如图,,是的切线,切点分别为,,交于点,的延长线交于点,下列结论不一定成立的是( )
第1题图
A. B.
C. D.平分
2.如图,,,均是的切线,切点分别是,,.若,,则的长是( )
第2题图
A.4 B.3 C.2 D.1
3.[2024岳阳模拟]如图,,是的切线,,为切点,是的直径,若 ,则的度数为( )
第3题图
A. B. C. D.
4.如图,为外一点,,分别切于点,,切于点,分别交,于点,.若,则的周长为__.
第4题图
5.如图,,是的两条切线,,是切点,,是上两点,已知 , ,求的度数.
第5题图
B组·能力提升 强化突破
6.如图,将一把直尺,一个 的直角三角板和一张光盘如图摆放,为 角与直尺的交点,,则光盘的直径是( )
第6题图
A.3 B. C.6 D.
7.[2024泸州]如图,,是的切线,切点为,,点,在上,若 ,则( )
第7题图
A. B. C. D.
8.如图,在中, , ,以为直径作交于点.过点作的切线交于点.求证:.
C组·核心素养拓展 素养渗透
9.【几何直观,推理能力】我们学习了利用尺规作图平分任意一个角,而“利用尺规作图三等分任意一个角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具——三分角器.图①是它的示意图,其中与半圆的直径在同一直线上,且的长度与半圆的半径相等;与垂直于点,足够长.
三分角器的使用方法如图②所示,若要把三等分,只需适当放置三分角器,使经过的顶点,点落在边上,半圆与另一边恰好相切,切点为,则,就把三等分了.
根据该操作过程,回答问题:
(1) 直线与半圆的位置关系是____,依据是____________________________________________________________________;
(2) 求证:;
(3) 若被测量的 ,,则的长度至少为______________,才能保证该三分角器能够三等分该角.(用含有 ,的代数式表示)
*2.5.3 切线长定理
课堂导学
知识梳理
线段的长; 相等; 平分
例题引路
【点悟】 切线长定理是等腰三角形、垂径定理、勾股定理的一个大组合,它是连接圆内与圆外的一个桥梁,利用它既可以得到线段相等,也可以得到角相等.通过本题,我们可以得到两个结论:(1);(2).
【思路分析】直接利用切线长定理得出,,进而得出答案;
例 (1) 【规范解答】,,是 的切线,,
,,.
.
【思路分析】利用切线的性质以及四边形内角和定理得出答案.
(2) ,,是 的切线,
,,,,,
,.
又 ,
.
A组·基础达标 逐点击破
知识点 切线长定理
1.D 2.C 3.B
4.16
5.解:,是的两条切线,,
.
, ,
.
, ,
.
四边形是的内接四边形,
,
.
B组·能力提升 强化突破
6.D 7.C
8.证明:如答图,连接,.
第8题答图
,,
是的切线.
是的切线,,
平分.
, ,
,
,
,,
.
C组·核心素养拓展 素养渗透
9.(1) 相切; 是半圆的直径,与垂直于点
(2) 证明:如答图,连接.
第9题答图
与垂直于点,
.
在和中,
,.
,为半圆的切线,
,.
(3)
[解析] ,,,
.
,,
,
的长度至少为时,才能保证该三分角器能够三等分该角.
A组·基础达标 逐点击破
知识点 切线长定理
1.如图,,是的切线,切点分别为,,交于点,的延长线交于点,下列结论不一定成立的是( )
第1题图
A. B.
C. D.平分
2.如图,,,均是的切线,切点分别是,,.若,,则的长是( )
第2题图
A.4 B.3 C.2 D.1
3.[2024岳阳模拟]如图,,是的切线,,为切点,是的直径,若 ,则的度数为( )
第3题图
A. B. C. D.
4.如图,为外一点,,分别切于点,,切于点,分别交,于点,.若,则的周长为__.
第4题图
5.如图,,是的两条切线,,是切点,,是上两点,已知 , ,求的度数.
第5题图
B组·能力提升 强化突破
6.如图,将一把直尺,一个 的直角三角板和一张光盘如图摆放,为 角与直尺的交点,,则光盘的直径是( )
第6题图
A.3 B. C.6 D.
7.[2024泸州]如图,,是的切线,切点为,,点,在上,若 ,则( )
第7题图
A. B. C. D.
8.如图,在中, , ,以为直径作交于点.过点作的切线交于点.求证:.
C组·核心素养拓展 素养渗透
9.【几何直观,推理能力】我们学习了利用尺规作图平分任意一个角,而“利用尺规作图三等分任意一个角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具——三分角器.图①是它的示意图,其中与半圆的直径在同一直线上,且的长度与半圆的半径相等;与垂直于点,足够长.
三分角器的使用方法如图②所示,若要把三等分,只需适当放置三分角器,使经过的顶点,点落在边上,半圆与另一边恰好相切,切点为,则,就把三等分了.
根据该操作过程,回答问题:
(1) 直线与半圆的位置关系是____,依据是____________________________________________________________________;
(2) 求证:;
(3) 若被测量的 ,,则的长度至少为______________,才能保证该三分角器能够三等分该角.(用含有 ,的代数式表示)
*2.5.3 切线长定理
课堂导学
知识梳理
线段的长; 相等; 平分
例题引路
【点悟】 切线长定理是等腰三角形、垂径定理、勾股定理的一个大组合,它是连接圆内与圆外的一个桥梁,利用它既可以得到线段相等,也可以得到角相等.通过本题,我们可以得到两个结论:(1);(2).
【思路分析】直接利用切线长定理得出,,进而得出答案;
例 (1) 【规范解答】,,是 的切线,,
,,.
.
【思路分析】利用切线的性质以及四边形内角和定理得出答案.
(2) ,,是 的切线,
,,,,,
,.
又 ,
.
A组·基础达标 逐点击破
知识点 切线长定理
1.D 2.C 3.B
4.16
5.解:,是的两条切线,,
.
, ,
.
, ,
.
四边形是的内接四边形,
,
.
B组·能力提升 强化突破
6.D 7.C
8.证明:如答图,连接,.
第8题答图
,,
是的切线.
是的切线,,
平分.
, ,
,
,
,,
.
C组·核心素养拓展 素养渗透
9.(1) 相切; 是半圆的直径,与垂直于点
(2) 证明:如答图,连接.
第9题答图
与垂直于点,
.
在和中,
,.
,为半圆的切线,
,.
(3)
[解析] ,,,
.
,,
,
的长度至少为时,才能保证该三分角器能够三等分该角.
