第1章 二次函数 质量评估(含答案)2024-2025学年数学湘教版九年级下册
文档属性
| 名称 | 第1章 二次函数 质量评估(含答案)2024-2025学年数学湘教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 21:43:27 | ||
图片预览


文档简介
第1章 二次函数 质量评估
[时间:120分钟 分值:120分]
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数是二次函数的是( )
A. B.
C. D.
2.对于抛物线的图象与性质,下列说法错误的是( )
A.抛物线的开口向上
B.对称轴为直线
C.顶点坐标为
D.当时,有最小值,最小值为3
3.抛物线先向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,抛物线经过点,对称轴为直线.若,则的取值范围是( )
第4题图
A. B.
C. D.或
5.已知二次函数的图象如图所示,则一次函数的图象一定不经过( )
第5题图
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知,,是抛物线上的三点,则( )
A. B. C. D.
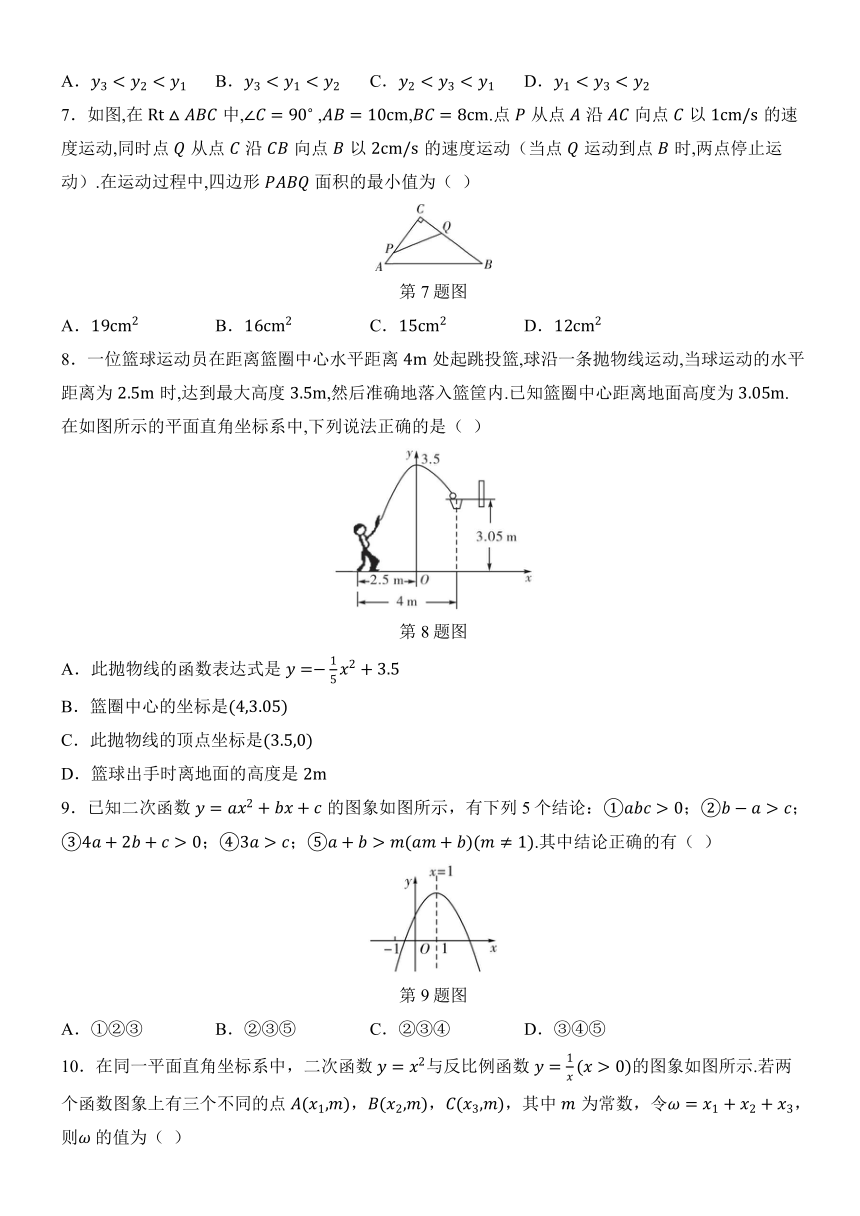
7.如图,在中, ,,.点从点沿向点以的速度运动,同时点从点沿向点以的速度运动(当点运动到点时,两点停止运动).在运动过程中,四边形面积的最小值为( )
第7题图
A. B. C. D.
8.一位篮球运动员在距离篮圈中心水平距离处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为时,达到最大高度,然后准确地落入篮筐内.已知篮圈中心距离地面高度为.在如图所示的平面直角坐标系中,下列说法正确的是( )
第8题图
A.此抛物线的函数表达式是
B.篮圈中心的坐标是
C.此抛物线的顶点坐标是
D.篮球出手时离地面的高度是
9.已知二次函数的图象如图所示,有下列5个结论:;;;;.其中结论正确的有( )
第9题图
A.①②③ B.②③⑤ C.②③④ D.③④⑤
10.在同一平面直角坐标系中,二次函数与反比例函数的图象如图所示.若两个函数图象上有三个不同的点,,,其中为常数,令,则 的值为( )
第10题图
A.1 B. C. D.
二、填空题(本题共8个小题,每小题3分,共24分)
11.二次函数的最大值是____.
12.若抛物线与轴只有一个交点,则____.
13.将二次函数化为的形式为____________________.
14.顶点坐标为且过点的抛物线的函数表达式为________________________.
15.如图,将小球以一定的速度沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度与飞行时间之间具有函数关系:,则当小球的飞行高度达到最高时,飞行时间____.
第15题图
16.在平面直角坐标系中,将抛物线先绕原点旋转 ,再向下平移5个单位,所得到的抛物线的顶点坐标是____________.
17.如图是抛物线形拱桥,当拱顶离水面时,水面宽.若水面下降,则水面宽度为________.
第17题图
18.如图,已知是二次函数的图象上的一动点,轴于点,连接.小华用几何画板软件对线段,的数量关系进行了探讨,发现是一个定值,则这个定值为____.
第18题图
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
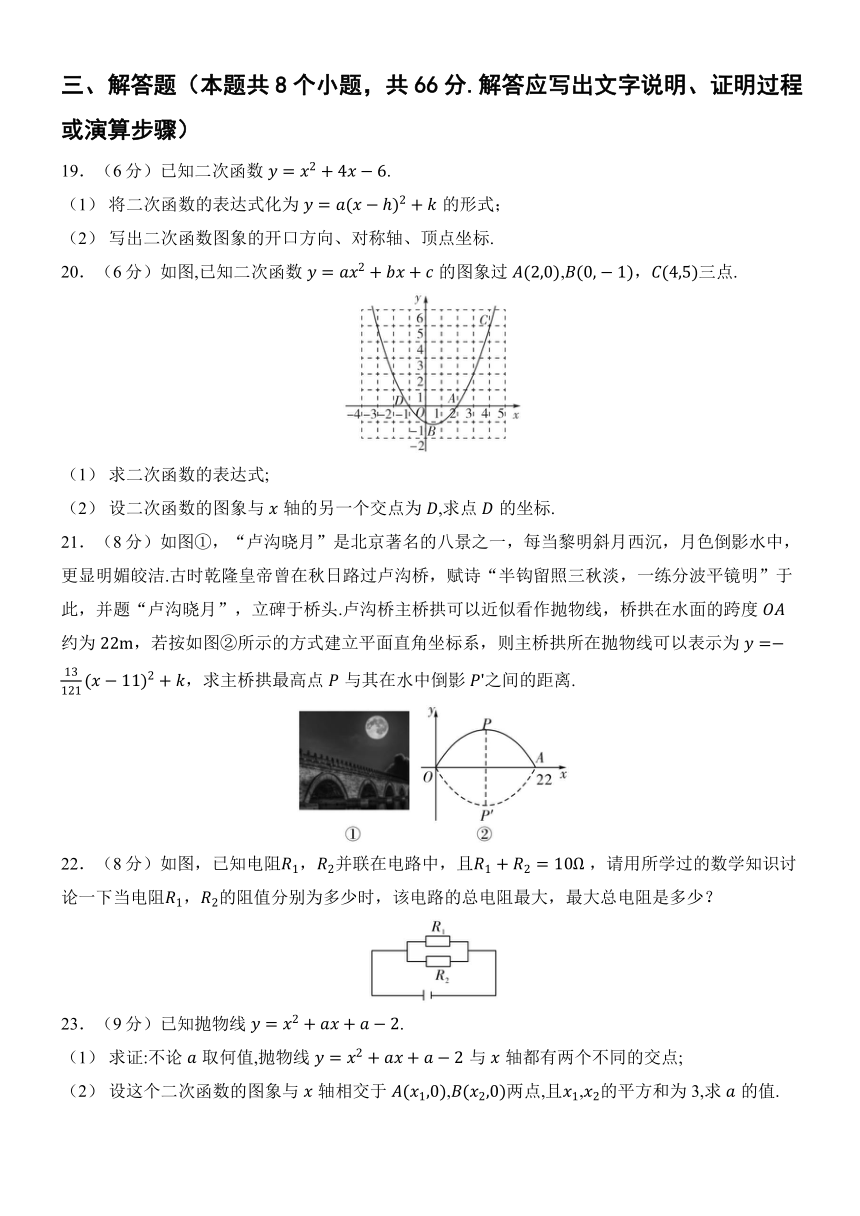
19.(6分)已知二次函数.
(1) 将二次函数的表达式化为的形式;
(2) 写出二次函数图象的开口方向、对称轴、顶点坐标.
20.(6分)如图,已知二次函数的图象过,,三点.
(1) 求二次函数的表达式;
(2) 设二次函数的图象与轴的另一个交点为,求点的坐标.
21.(8分)如图①,“卢沟晓月”是北京著名的八景之一,每当黎明斜月西沉,月色倒影水中,更显明媚皎洁.古时乾隆皇帝曾在秋日路过卢沟桥,赋诗“半钩留照三秋淡,一练分波平镜明”于此,并题“卢沟晓月”,立碑于桥头.卢沟桥主桥拱可以近似看作抛物线,桥拱在水面的跨度约为,若按如图②所示的方式建立平面直角坐标系,则主桥拱所在抛物线可以表示为,求主桥拱最高点与其在水中倒影之间的距离.
22.(8分)如图,已知电阻,并联在电路中,且 ,请用所学过的数学知识讨论一下当电阻,的阻值分别为多少时,该电路的总电阻最大,最大总电阻是多少?
23.(9分)已知抛物线.
(1) 求证:不论取何值,抛物线与轴都有两个不同的交点;
(2) 设这个二次函数的图象与轴相交于,两点,且,的平方和为3,求的值.
24.(9分)超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加元,每天售出件.
(1) 请写出关于的函数表达式(要求写出自变量的取值范围);
(2) 设超市每天销售这种玩具可获利元,当的值为多少时,获利最大,最大值是多少?
25.(10分)在平面直角坐标系中,,是抛物线上任意两点,设抛物线的对称轴为直线.
(1) 若对于,,有,求的值;
(2) 若对于,,都有,求的取值范围.
26.(10分)如图,抛物线过点,,.
(1) 求抛物线的表达式.
(2) 设是直线上方抛物线上一点,求出面积的最大值及此时点的坐标.
(3) 若是抛物线的对称轴上一动点,为坐标平面内一点,是否存在以为边、点,,,为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
第1章质量评估
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.B 2.B 3.A 4.D 5.D 6.B 7.C 8.A 9.B 10.D
二、填空题(本题共8个小题,每小题3分,共24分)
11.5
12.9
13.
14.
15.2
16.
17.
18.2
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(1) 解:.
(2) ,,
二次函数图象的开口向上,对称轴是直线,顶点坐标是.
20.(1) 解:将,,代入二次函数,得解得
二次函数的表达式为.
(2) 当时,,
解得,,
点的坐标为.
21.解:由二次函数的图象可知,在抛物线上,
把代入,得
,解得.
.
主桥拱最高点的坐标为.
点和点关于轴对称,
.
答:主桥拱最高点与其在水中倒影之间的距离是.
22.解:由题意,得,
又 ,
.
, 当时,有最大值,最大值为.
,
答:当电阻,的阻值分别为 , 时,该电路的总电阻最大,最大总电阻为 .
23.(1) 证明:,
不论取何值,抛物线与轴都有两个不同的交点.
(2) 解:,,
,解得.
24.(1) 解:由题意,得.
(2) 由题意,得.
, 当时,随的增大而增大,
, 当时,取得最大值,.
25.(1) 解: 对于,,有,
,
,.
对称轴直线为,.
(2) ,,,.
,,
离对称轴更近,
又,则与的中点在对称轴的右侧,
,即.
26.(1) 解:由题意,得,
抛物线过点,,解得,
故抛物线的表达式为.
(2) 设直线的表达式为,将,代入,
得解得
直线的表达式为,
如答图,过点作轴的平行线交于点,
设,则,
,
,
面积的最大值为,此时点的坐标为.
第26题答图
(3) 存在.
抛物线的表达式为,
对轴轴为直线.
设,,
若为菱形的边,此时菱形为,则,
即,解得,.
,.
若为菱形的对角线,此时菱形为,则,
即,解得,.
,.
综上所述,点的坐标为或或或
.
[时间:120分钟 分值:120分]
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数是二次函数的是( )
A. B.
C. D.
2.对于抛物线的图象与性质,下列说法错误的是( )
A.抛物线的开口向上
B.对称轴为直线
C.顶点坐标为
D.当时,有最小值,最小值为3
3.抛物线先向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,抛物线经过点,对称轴为直线.若,则的取值范围是( )
第4题图
A. B.
C. D.或
5.已知二次函数的图象如图所示,则一次函数的图象一定不经过( )
第5题图
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知,,是抛物线上的三点,则( )
A. B. C. D.
7.如图,在中, ,,.点从点沿向点以的速度运动,同时点从点沿向点以的速度运动(当点运动到点时,两点停止运动).在运动过程中,四边形面积的最小值为( )
第7题图
A. B. C. D.
8.一位篮球运动员在距离篮圈中心水平距离处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为时,达到最大高度,然后准确地落入篮筐内.已知篮圈中心距离地面高度为.在如图所示的平面直角坐标系中,下列说法正确的是( )
第8题图
A.此抛物线的函数表达式是
B.篮圈中心的坐标是
C.此抛物线的顶点坐标是
D.篮球出手时离地面的高度是
9.已知二次函数的图象如图所示,有下列5个结论:;;;;.其中结论正确的有( )
第9题图
A.①②③ B.②③⑤ C.②③④ D.③④⑤
10.在同一平面直角坐标系中,二次函数与反比例函数的图象如图所示.若两个函数图象上有三个不同的点,,,其中为常数,令,则 的值为( )
第10题图
A.1 B. C. D.
二、填空题(本题共8个小题,每小题3分,共24分)
11.二次函数的最大值是____.
12.若抛物线与轴只有一个交点,则____.
13.将二次函数化为的形式为____________________.
14.顶点坐标为且过点的抛物线的函数表达式为________________________.
15.如图,将小球以一定的速度沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度与飞行时间之间具有函数关系:,则当小球的飞行高度达到最高时,飞行时间____.
第15题图
16.在平面直角坐标系中,将抛物线先绕原点旋转 ,再向下平移5个单位,所得到的抛物线的顶点坐标是____________.
17.如图是抛物线形拱桥,当拱顶离水面时,水面宽.若水面下降,则水面宽度为________.
第17题图
18.如图,已知是二次函数的图象上的一动点,轴于点,连接.小华用几何画板软件对线段,的数量关系进行了探讨,发现是一个定值,则这个定值为____.
第18题图
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(6分)已知二次函数.
(1) 将二次函数的表达式化为的形式;
(2) 写出二次函数图象的开口方向、对称轴、顶点坐标.
20.(6分)如图,已知二次函数的图象过,,三点.
(1) 求二次函数的表达式;
(2) 设二次函数的图象与轴的另一个交点为,求点的坐标.
21.(8分)如图①,“卢沟晓月”是北京著名的八景之一,每当黎明斜月西沉,月色倒影水中,更显明媚皎洁.古时乾隆皇帝曾在秋日路过卢沟桥,赋诗“半钩留照三秋淡,一练分波平镜明”于此,并题“卢沟晓月”,立碑于桥头.卢沟桥主桥拱可以近似看作抛物线,桥拱在水面的跨度约为,若按如图②所示的方式建立平面直角坐标系,则主桥拱所在抛物线可以表示为,求主桥拱最高点与其在水中倒影之间的距离.
22.(8分)如图,已知电阻,并联在电路中,且 ,请用所学过的数学知识讨论一下当电阻,的阻值分别为多少时,该电路的总电阻最大,最大总电阻是多少?
23.(9分)已知抛物线.
(1) 求证:不论取何值,抛物线与轴都有两个不同的交点;
(2) 设这个二次函数的图象与轴相交于,两点,且,的平方和为3,求的值.
24.(9分)超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加元,每天售出件.
(1) 请写出关于的函数表达式(要求写出自变量的取值范围);
(2) 设超市每天销售这种玩具可获利元,当的值为多少时,获利最大,最大值是多少?
25.(10分)在平面直角坐标系中,,是抛物线上任意两点,设抛物线的对称轴为直线.
(1) 若对于,,有,求的值;
(2) 若对于,,都有,求的取值范围.
26.(10分)如图,抛物线过点,,.
(1) 求抛物线的表达式.
(2) 设是直线上方抛物线上一点,求出面积的最大值及此时点的坐标.
(3) 若是抛物线的对称轴上一动点,为坐标平面内一点,是否存在以为边、点,,,为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
第1章质量评估
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.B 2.B 3.A 4.D 5.D 6.B 7.C 8.A 9.B 10.D
二、填空题(本题共8个小题,每小题3分,共24分)
11.5
12.9
13.
14.
15.2
16.
17.
18.2
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(1) 解:.
(2) ,,
二次函数图象的开口向上,对称轴是直线,顶点坐标是.
20.(1) 解:将,,代入二次函数,得解得
二次函数的表达式为.
(2) 当时,,
解得,,
点的坐标为.
21.解:由二次函数的图象可知,在抛物线上,
把代入,得
,解得.
.
主桥拱最高点的坐标为.
点和点关于轴对称,
.
答:主桥拱最高点与其在水中倒影之间的距离是.
22.解:由题意,得,
又 ,
.
, 当时,有最大值,最大值为.
,
答:当电阻,的阻值分别为 , 时,该电路的总电阻最大,最大总电阻为 .
23.(1) 证明:,
不论取何值,抛物线与轴都有两个不同的交点.
(2) 解:,,
,解得.
24.(1) 解:由题意,得.
(2) 由题意,得.
, 当时,随的增大而增大,
, 当时,取得最大值,.
25.(1) 解: 对于,,有,
,
,.
对称轴直线为,.
(2) ,,,.
,,
离对称轴更近,
又,则与的中点在对称轴的右侧,
,即.
26.(1) 解:由题意,得,
抛物线过点,,解得,
故抛物线的表达式为.
(2) 设直线的表达式为,将,代入,
得解得
直线的表达式为,
如答图,过点作轴的平行线交于点,
设,则,
,
,
面积的最大值为,此时点的坐标为.
第26题答图
(3) 存在.
抛物线的表达式为,
对轴轴为直线.
设,,
若为菱形的边,此时菱形为,则,
即,解得,.
,.
若为菱形的对角线,此时菱形为,则,
即,解得,.
,.
综上所述,点的坐标为或或或
.
