第2章 圆 课时作业(含答案)2024-2025学年数学湘教版九年级下册
文档属性
| 名称 | 第2章 圆 课时作业(含答案)2024-2025学年数学湘教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 21:45:11 | ||
图片预览


文档简介
第2章 圆
整合提升 练就四能
类型之1 点与圆的位置关系
1.已知的半径为,点到圆心的距离,则点与的位置关系为( )
A.点在上 B.点在内
C.点在外 D.无法确定
类型之2 圆心角、弧、弦之间的关系
2.如图,已知在中,是直径,,则下列结论不一定成立的是( )
A. B.
C. D.点到,的距离相等
类型之3 垂径定理及其推论
3.如图,是的直径,弦于点,点在上,恰好过圆心,连接.
(1) 若,,求的直径;
(2) 若,求的度数.
类型之4 圆周角定理及其推论、圆内接四边形的性质
4.如图,四边形内接于,, ,连接,则( )
A. B. C. D.
5.如图,以的一边为直径的半圆与其他两边,的交点分别为点,,且.
(1) 试判断的形状,并说明理由;
(2) 已知半圆的半径为5,,求的值.
类型之5 切线的性质与判定
6.[2024南充]如图,在中,是直径,是弦,点是上一点,,,交于点,点为延长线上一点,且.
(1) 求证:是的切线.
(2) 若,,求的半径长.
类型之6 三角形的内切圆、切线长定理
7.[2024滨州]刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,中, ,,,的长分别为,,.则可以用含,,的式子表示出的内切圆直径,下列表达式错误的是( )
A. B.
C. D.
8.如图,,,分别切于点,,,且点在上,点在上.
(1) 若,则的周长是__;
(2) 若 ,则________.
类型之7 正多边形与圆
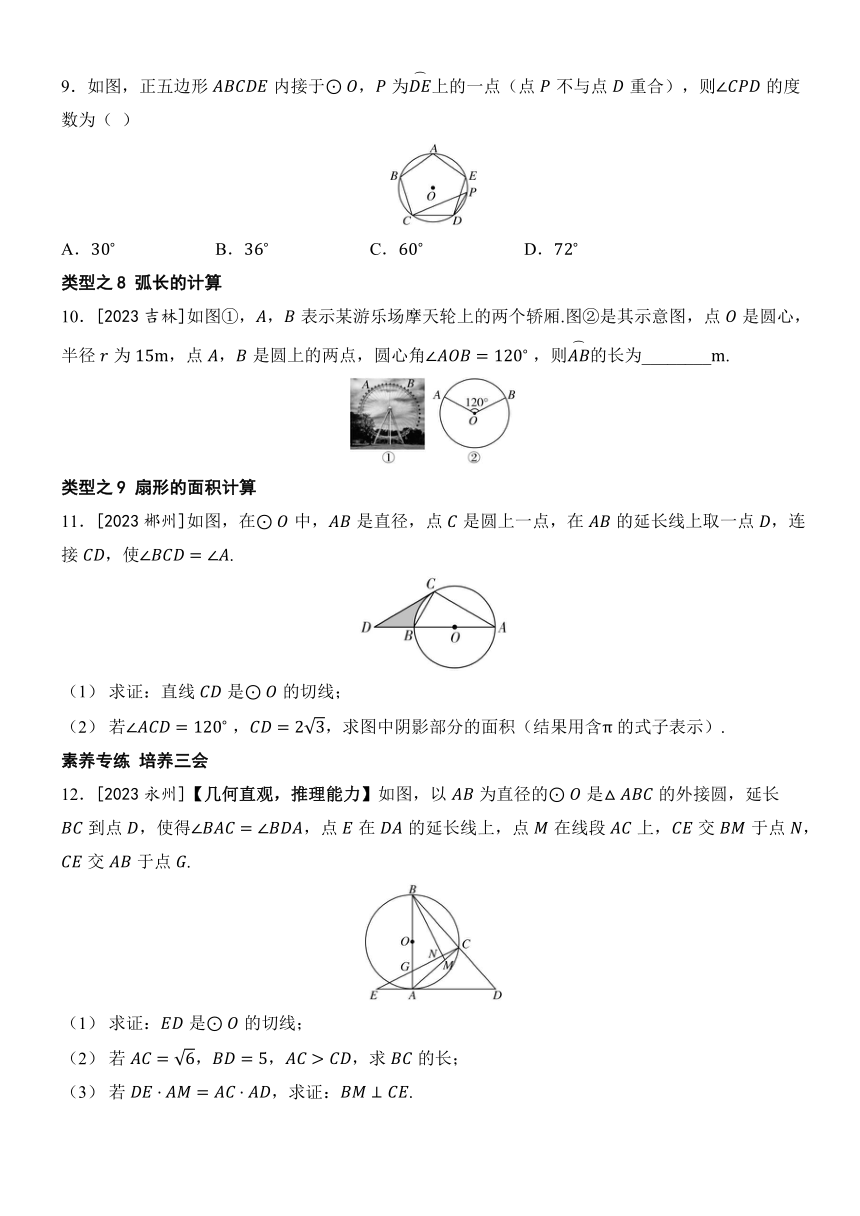
9.如图,正五边形内接于,为上的一点(点不与点重合),则的度数为( )
A. B. C. D.
类型之8 弧长的计算
10.[2023吉林]如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角 ,则的长为________.
类型之9 扇形的面积计算
11.[2023郴州]如图,在中,是直径,点是圆上一点,在的延长线上取一点,连接,使.
(1) 求证:直线是的切线;
(2) 若 ,,求图中阴影部分的面积(结果用含 的式子表示).
素养专练 培养三会
12.[2023永州]【几何直观,推理能力】如图,以为直径的是的外接圆,延长到点,使得,点在的延长线上,点在线段上,交于点,交于点.
(1) 求证:是的切线;
(2) 若,,,求的长;
(3) 若,求证:.
本章复习课
整合提升 练就四能
类型之1 点与圆的位置关系
1.B
类型之2 圆心角、弧、弦之间的关系
2.A
类型之3 垂径定理及其推论
3.(1) 解:,,
.
设,则.
在中,,
解得.
的直径是20.
(2) ,,
.
, .
类型之4 圆周角定理及其推论、圆内接四边形的性质
4.B
5.(1) 解:为等腰三角形.理由如下:
如答图,连接.
第5题答图
,,
即平分.
为半圆的直径,
,.
为等腰三角形,且.
(2) 为等腰三角形,,
,
.
在中,,,
.
为半圆的直径, .
,
.
在中,,,
.
.
类型之5 切线的性质与判定
6.(1) 证明:,
,
,且,
,
,
是的半径,且,
是的切线.
(2) 解:如答图,连接,
第6题答图
,,,
,
是的直径,
,
,
,
,
,
,
的半径长为.
类型之6 三角形的内切圆、切线长定理
7.D
8.(1) 20
(2)
类型之7 正多边形与圆
9.B
类型之8 弧长的计算
10.
类型之9 扇形的面积计算
11.(1) 证明:如答图,连接,
第11题答图
是的直径,
.
,,
.
.
.
是的半径,
直线是的切线.
(2) 解: , ,
,
.
在中,,,
,.
素养专练 培养三会
12.(1) 证明:是的直径,
,
.
,
,
,.
又是的半径,
是的切线.
(2) 解:, ,
,
,即.
,,,
解得或,
当时,(不合题意,舍去);
当时,.
的长为3.
(3) 证明:由(2)知,
,
.
,
,
.
,,
.
,
,
,.
整合提升 练就四能
类型之1 点与圆的位置关系
1.已知的半径为,点到圆心的距离,则点与的位置关系为( )
A.点在上 B.点在内
C.点在外 D.无法确定
类型之2 圆心角、弧、弦之间的关系
2.如图,已知在中,是直径,,则下列结论不一定成立的是( )
A. B.
C. D.点到,的距离相等
类型之3 垂径定理及其推论
3.如图,是的直径,弦于点,点在上,恰好过圆心,连接.
(1) 若,,求的直径;
(2) 若,求的度数.
类型之4 圆周角定理及其推论、圆内接四边形的性质
4.如图,四边形内接于,, ,连接,则( )
A. B. C. D.
5.如图,以的一边为直径的半圆与其他两边,的交点分别为点,,且.
(1) 试判断的形状,并说明理由;
(2) 已知半圆的半径为5,,求的值.
类型之5 切线的性质与判定
6.[2024南充]如图,在中,是直径,是弦,点是上一点,,,交于点,点为延长线上一点,且.
(1) 求证:是的切线.
(2) 若,,求的半径长.
类型之6 三角形的内切圆、切线长定理
7.[2024滨州]刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,中, ,,,的长分别为,,.则可以用含,,的式子表示出的内切圆直径,下列表达式错误的是( )
A. B.
C. D.
8.如图,,,分别切于点,,,且点在上,点在上.
(1) 若,则的周长是__;
(2) 若 ,则________.
类型之7 正多边形与圆
9.如图,正五边形内接于,为上的一点(点不与点重合),则的度数为( )
A. B. C. D.
类型之8 弧长的计算
10.[2023吉林]如图①,,表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点是圆心,半径为,点,是圆上的两点,圆心角 ,则的长为________.
类型之9 扇形的面积计算
11.[2023郴州]如图,在中,是直径,点是圆上一点,在的延长线上取一点,连接,使.
(1) 求证:直线是的切线;
(2) 若 ,,求图中阴影部分的面积(结果用含 的式子表示).
素养专练 培养三会
12.[2023永州]【几何直观,推理能力】如图,以为直径的是的外接圆,延长到点,使得,点在的延长线上,点在线段上,交于点,交于点.
(1) 求证:是的切线;
(2) 若,,,求的长;
(3) 若,求证:.
本章复习课
整合提升 练就四能
类型之1 点与圆的位置关系
1.B
类型之2 圆心角、弧、弦之间的关系
2.A
类型之3 垂径定理及其推论
3.(1) 解:,,
.
设,则.
在中,,
解得.
的直径是20.
(2) ,,
.
, .
类型之4 圆周角定理及其推论、圆内接四边形的性质
4.B
5.(1) 解:为等腰三角形.理由如下:
如答图,连接.
第5题答图
,,
即平分.
为半圆的直径,
,.
为等腰三角形,且.
(2) 为等腰三角形,,
,
.
在中,,,
.
为半圆的直径, .
,
.
在中,,,
.
.
类型之5 切线的性质与判定
6.(1) 证明:,
,
,且,
,
,
是的半径,且,
是的切线.
(2) 解:如答图,连接,
第6题答图
,,,
,
是的直径,
,
,
,
,
,
,
的半径长为.
类型之6 三角形的内切圆、切线长定理
7.D
8.(1) 20
(2)
类型之7 正多边形与圆
9.B
类型之8 弧长的计算
10.
类型之9 扇形的面积计算
11.(1) 证明:如答图,连接,
第11题答图
是的直径,
.
,,
.
.
.
是的半径,
直线是的切线.
(2) 解: , ,
,
.
在中,,,
,.
素养专练 培养三会
12.(1) 证明:是的直径,
,
.
,
,
,.
又是的半径,
是的切线.
(2) 解:, ,
,
,即.
,,,
解得或,
当时,(不合题意,舍去);
当时,.
的长为3.
(3) 证明:由(2)知,
,
.
,
,
.
,,
.
,
,
,.
