第3章 投影与视图 质量评估(含答案)2024-2025学年数学湘教版九年级下册
文档属性
| 名称 | 第3章 投影与视图 质量评估(含答案)2024-2025学年数学湘教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 359.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览


文档简介
第3章 投影与视图 质量评估
[时间:120分钟 分值:120分]
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,则它的正投影是( )
A. B.
C. D.
2.如图,该几何体的主视图是( )
A. B. C. D.
3.如图所示的工件,其俯视图是( )
A. B.
C. D.
4.如图所示的几何体是由一个球体和一个圆柱组成的,它的俯视图是( )
A. B. C. D.
5.葫芦在我国古代被看作吉祥之物.如图是一个工艺葫芦的示意图,关于它的三视图说法正确的是( )
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图都相同
6.如图是一个正方体的表面展开图,把展开图折叠成正方体后,“你”字所在面的相对面上的字是( )
A.我 B.中 C.国 D.梦
7.某几何体的三视图如图所示,则该几何体为( )
A. B.
C. D.
8.如图,圆锥底面半径,母线长,则这个圆锥的侧面积为( )
A. B. C. D.
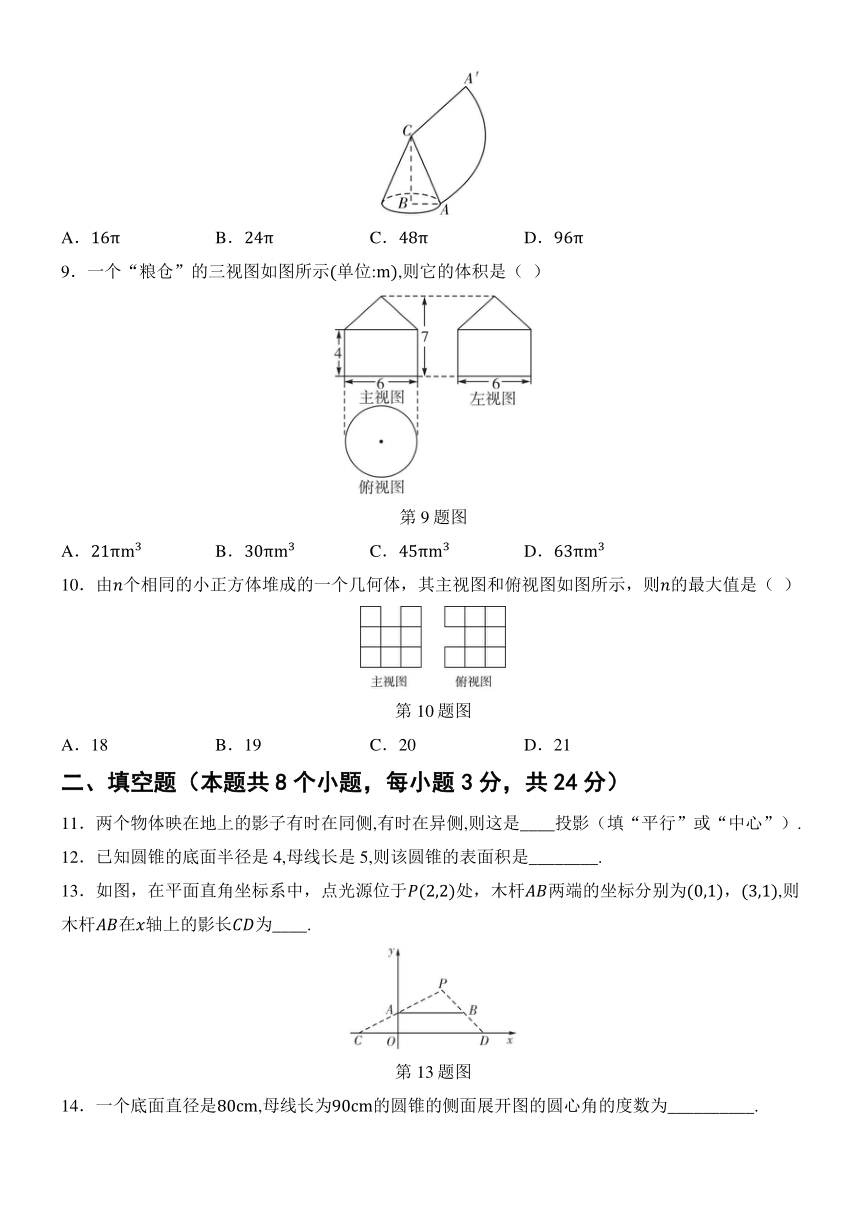
9.一个“粮仓”的三视图如图所示单位:,则它的体积是( )
第9题图
A. B. C. D.
10.由个相同的小正方体堆成的一个几何体,其主视图和俯视图如图所示,则的最大值是( )
第10题图
A.18 B.19 C.20 D.21
二、填空题(本题共8个小题,每小题3分,共24分)
11.两个物体映在地上的影子有时在同侧,有时在异侧,则这是____投影(填“平行”或“中心”).
12.已知圆锥的底面半径是4,母线长是5,则该圆锥的表面积是________.
13.如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为,,则木杆在轴上的影长为____.
第13题图
14.一个底面直径是,母线长为的圆锥的侧面展开图的圆心角的度数为__________.
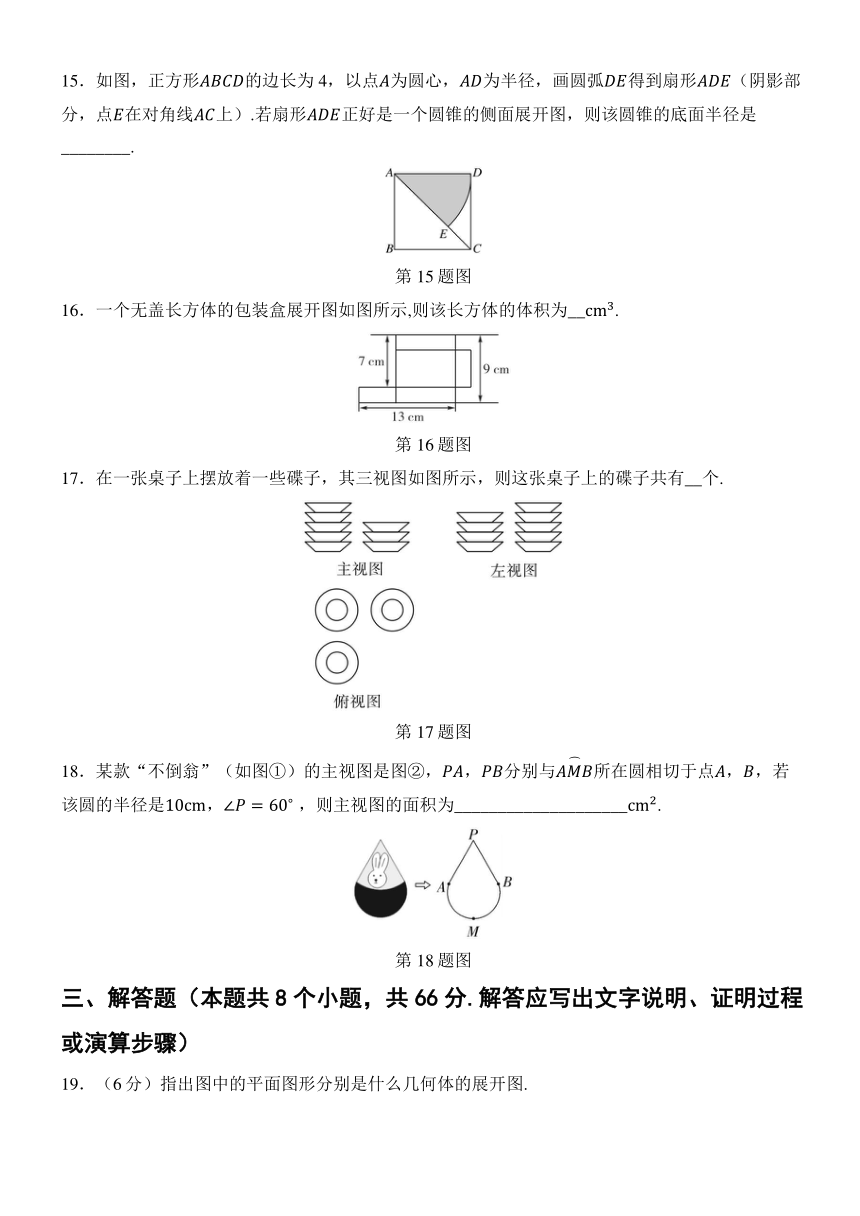
15.如图,正方形的边长为4,以点为圆心,为半径,画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面半径是________.
第15题图
16.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为__.
第16题图
17.在一张桌子上摆放着一些碟子,其三视图如图所示,则这张桌子上的碟子共有__个.
第17题图
18.某款“不倒翁”(如图①)的主视图是图②,,分别与所在圆相切于点,,若该圆的半径是, ,则主视图的面积为____________________.
第18题图
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(6分)指出图中的平面图形分别是什么几何体的展开图.
20.(6分)画出图中组合体的三视图.
21.(8分)如图,小华、小军和小丽同时站在路灯下,其中小军和小丽的影子分别是线段,.
(1) 请你在图中画出路灯灯泡所在的位置(用点表示);
(2) 画出小华此时在路灯下的影子(用线段表示).
22.(8分)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的底面半径,扇形的圆心角 ,求该圆锥的高.
23.(9分)如图①是由一些棱长都为的小正方体组合成的简单几何体.
① ②
(1) 该几何体的主视图已画出,请在图②中画出它的左视图和俯视图;
(2) 如果在这个几何体上再添加一些同样大小的小正方体,并保持俯视图和左视图不变,那么最多可以再添加____个小正方体.
24.(9分)有一种牛奶软包装盒如图①所示,为了生产这种包装盒,需要先画出该包装盒的展开图纸样.
(1) 图②给出的四种展开图纸样A,B,C,D,其中正确的有______________.
(2) 求包装盒的表面积(侧面积与两个底面积的和).
25.(10分)小亮要利用废纸板做一个三棱柱形状的无盖笔筒,其底面是直角三角形,设计三棱柱的立体模型如图所示.
(1) 请画出该立体模型的三视图;
(2) 该笔筒至少要用多少平方厘米的废纸板?
26.(10分)某冷饮厂要加工一批冰激凌蛋筒,设计师给出了封闭蛋筒的三视图(如图所示).请你按照三视图,确定制作每个蛋筒所需的包装材料的面积 取,不计损耗.
第3章质量评估
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.D 2.C 3.C 4.C 5.A 6.D 7.B 8.C 9.C 10.D
二、填空题(本题共8个小题,每小题3分,共24分)
11.中心
12.
13.6
14.
15.
16.80
17.12
18.
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.解:长方体;圆锥;圆柱.
20.解:如答图.
第20题答图
21.(1) 解:如答图,点即所求的点.
第21题答图
(2) 如答图,线段即小华此时在路灯下的影子.
第21题答图
22.解:如答图,设底面圆的圆心为点,母线为,连接,则.
第22题答图
由题意,得.
,.
在中,由勾股定理,得.
答:该圆锥的高为.
23.(1) 解:如答图.
第23题答图
(2) 6
24.(1) ,
(2) 解:,
,
.
25.(1) 解:三视图如答图.
第25题答图
(2) 底面是直角三角形,
斜边长为.
,,.
答:该笔筒至少要用的废纸板.
26.解:由三视图可知,蛋筒是圆锥形的,如答图所示.
第26题答图
蛋筒的母线长为,底面半径为.
由展开图可知,.
答:制作每个蛋筒所需的包装材料的面积约为.
[时间:120分钟 分值:120分]
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,则它的正投影是( )
A. B.
C. D.
2.如图,该几何体的主视图是( )
A. B. C. D.
3.如图所示的工件,其俯视图是( )
A. B.
C. D.
4.如图所示的几何体是由一个球体和一个圆柱组成的,它的俯视图是( )
A. B. C. D.
5.葫芦在我国古代被看作吉祥之物.如图是一个工艺葫芦的示意图,关于它的三视图说法正确的是( )
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图都相同
6.如图是一个正方体的表面展开图,把展开图折叠成正方体后,“你”字所在面的相对面上的字是( )
A.我 B.中 C.国 D.梦
7.某几何体的三视图如图所示,则该几何体为( )
A. B.
C. D.
8.如图,圆锥底面半径,母线长,则这个圆锥的侧面积为( )
A. B. C. D.
9.一个“粮仓”的三视图如图所示单位:,则它的体积是( )
第9题图
A. B. C. D.
10.由个相同的小正方体堆成的一个几何体,其主视图和俯视图如图所示,则的最大值是( )
第10题图
A.18 B.19 C.20 D.21
二、填空题(本题共8个小题,每小题3分,共24分)
11.两个物体映在地上的影子有时在同侧,有时在异侧,则这是____投影(填“平行”或“中心”).
12.已知圆锥的底面半径是4,母线长是5,则该圆锥的表面积是________.
13.如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为,,则木杆在轴上的影长为____.
第13题图
14.一个底面直径是,母线长为的圆锥的侧面展开图的圆心角的度数为__________.
15.如图,正方形的边长为4,以点为圆心,为半径,画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面半径是________.
第15题图
16.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为__.
第16题图
17.在一张桌子上摆放着一些碟子,其三视图如图所示,则这张桌子上的碟子共有__个.
第17题图
18.某款“不倒翁”(如图①)的主视图是图②,,分别与所在圆相切于点,,若该圆的半径是, ,则主视图的面积为____________________.
第18题图
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(6分)指出图中的平面图形分别是什么几何体的展开图.
20.(6分)画出图中组合体的三视图.
21.(8分)如图,小华、小军和小丽同时站在路灯下,其中小军和小丽的影子分别是线段,.
(1) 请你在图中画出路灯灯泡所在的位置(用点表示);
(2) 画出小华此时在路灯下的影子(用线段表示).
22.(8分)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的底面半径,扇形的圆心角 ,求该圆锥的高.
23.(9分)如图①是由一些棱长都为的小正方体组合成的简单几何体.
① ②
(1) 该几何体的主视图已画出,请在图②中画出它的左视图和俯视图;
(2) 如果在这个几何体上再添加一些同样大小的小正方体,并保持俯视图和左视图不变,那么最多可以再添加____个小正方体.
24.(9分)有一种牛奶软包装盒如图①所示,为了生产这种包装盒,需要先画出该包装盒的展开图纸样.
(1) 图②给出的四种展开图纸样A,B,C,D,其中正确的有______________.
(2) 求包装盒的表面积(侧面积与两个底面积的和).
25.(10分)小亮要利用废纸板做一个三棱柱形状的无盖笔筒,其底面是直角三角形,设计三棱柱的立体模型如图所示.
(1) 请画出该立体模型的三视图;
(2) 该笔筒至少要用多少平方厘米的废纸板?
26.(10分)某冷饮厂要加工一批冰激凌蛋筒,设计师给出了封闭蛋筒的三视图(如图所示).请你按照三视图,确定制作每个蛋筒所需的包装材料的面积 取,不计损耗.
第3章质量评估
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.D 2.C 3.C 4.C 5.A 6.D 7.B 8.C 9.C 10.D
二、填空题(本题共8个小题,每小题3分,共24分)
11.中心
12.
13.6
14.
15.
16.80
17.12
18.
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.解:长方体;圆锥;圆柱.
20.解:如答图.
第20题答图
21.(1) 解:如答图,点即所求的点.
第21题答图
(2) 如答图,线段即小华此时在路灯下的影子.
第21题答图
22.解:如答图,设底面圆的圆心为点,母线为,连接,则.
第22题答图
由题意,得.
,.
在中,由勾股定理,得.
答:该圆锥的高为.
23.(1) 解:如答图.
第23题答图
(2) 6
24.(1) ,
(2) 解:,
,
.
25.(1) 解:三视图如答图.
第25题答图
(2) 底面是直角三角形,
斜边长为.
,,.
答:该笔筒至少要用的废纸板.
26.解:由三视图可知,蛋筒是圆锥形的,如答图所示.
第26题答图
蛋筒的母线长为,底面半径为.
由展开图可知,.
答:制作每个蛋筒所需的包装材料的面积约为.
