期中质量评估(含答案)2024-2025学年数学湘教版九年级下册
文档属性
| 名称 | 期中质量评估(含答案)2024-2025学年数学湘教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 277.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览



文档简介
期中质量评估
[时间:120分钟 分值:120分]
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,属于二次函数的是( )
A. B.
C. D.
2.关于二次函数的图象,下列说法正确的是( )
A.开口向上 B.顶点坐标为
C.与轴交点为 D.对称轴为直线
3.在平面直角坐标系中,将抛物线先向左平移2个单位,再向上平移3个单位,则平移后抛物线的函数表达式是( )
A. B.
C. D.
4.在平面直角坐标系中,的直径为10.若圆心为坐标原点,则点与的位置关系是( )
A.点在上 B.点在外
C.点在内 D.无法确定
5.已知正六边形内接于,若的直径为2,则该正六边形的周长是( )
A.12 B. C.6 D.
6.如图,抛物线与轴交于,两点,与轴交于点,连接,,则的面积为( )
第6题图
A.1 B.2 C.4 D.8
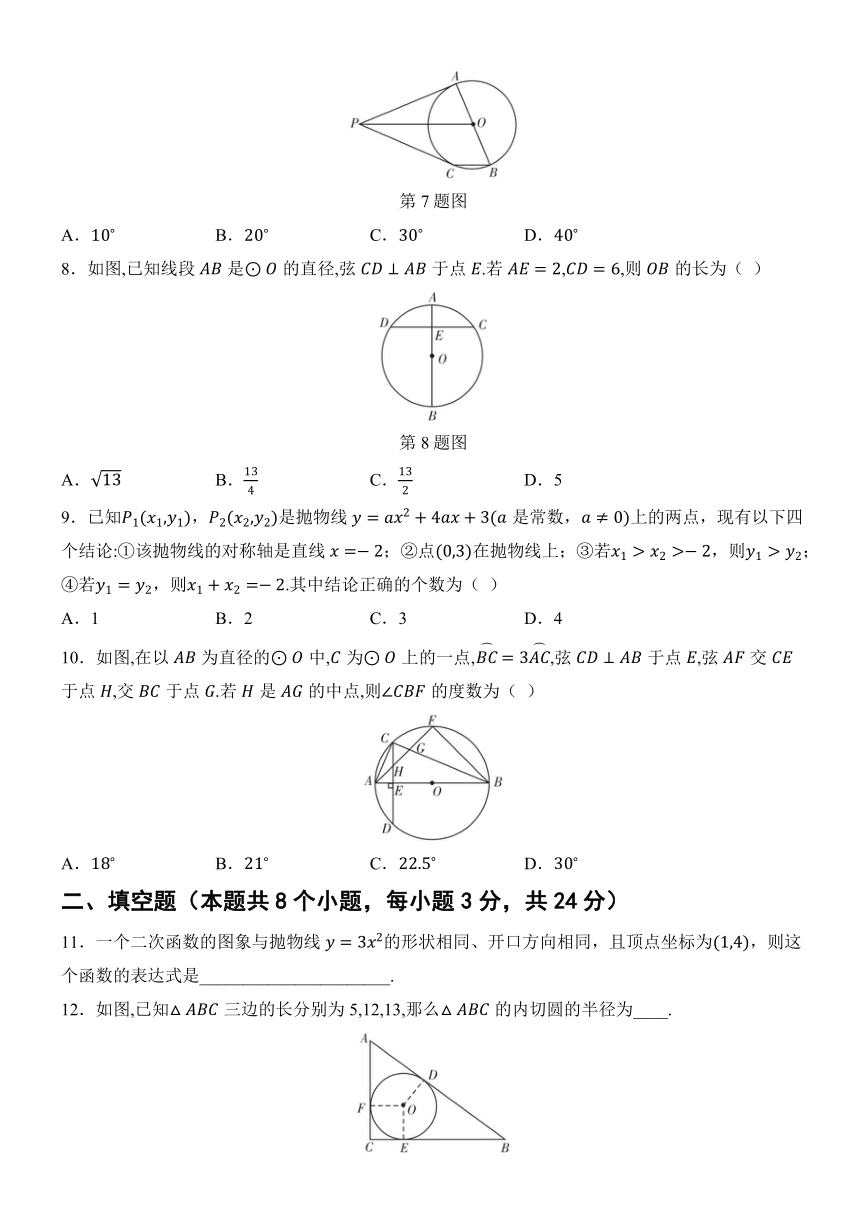
7.如图,是的直径,与相切于点,交于点.若 ,则的度数为( )
第7题图
A. B. C. D.
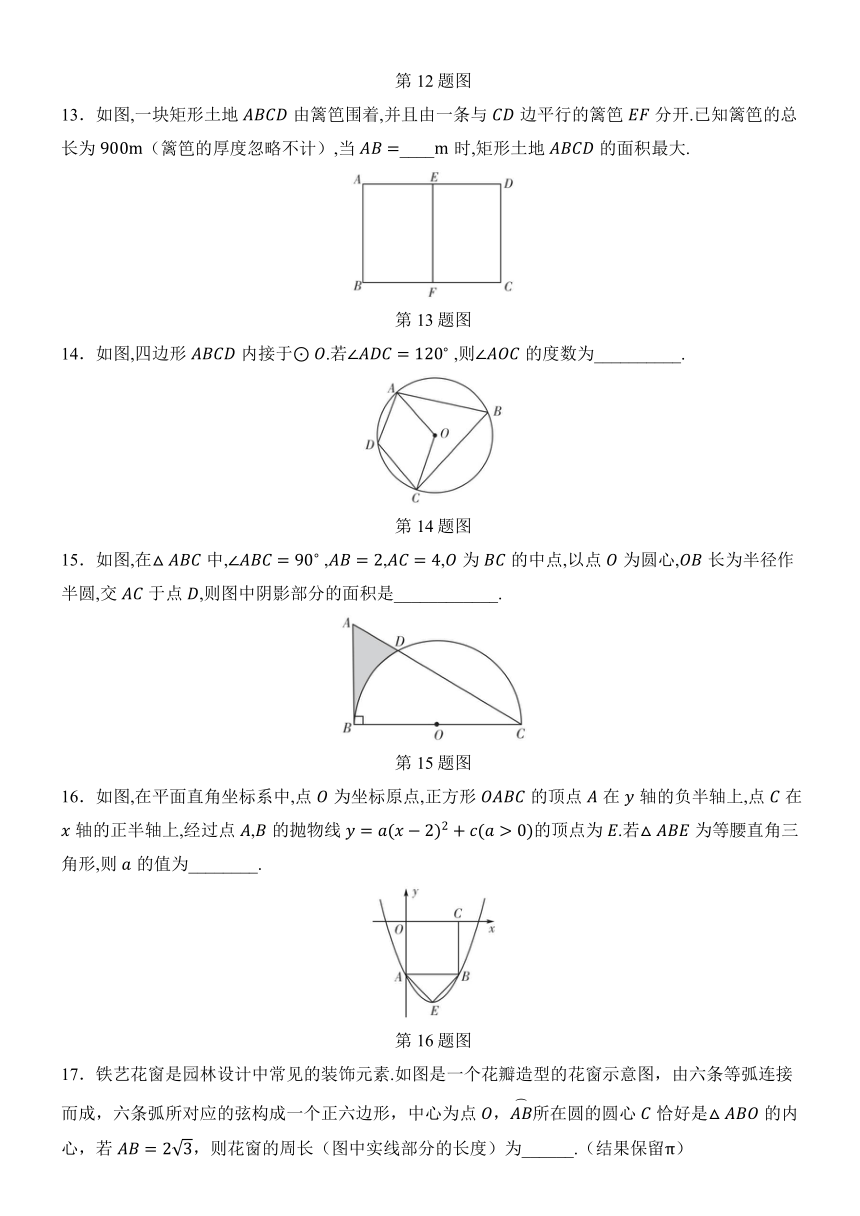
8.如图,已知线段是的直径,弦于点.若,,则的长为( )
第8题图
A. B. C. D.5
9.已知,是抛物线是常数,上的两点,现有以下四个结论:①该抛物线的对称轴是直线;②点在抛物线上;③若,则;④若,则.其中结论正确的个数为( )
A.1 B.2 C.3 D.4
10.如图,在以为直径的中,为上的一点,,弦于点,弦交于点,交于点.若是的中点,则的度数为( )
A. B. C. D.
二、填空题(本题共8个小题,每小题3分,共24分)
11.一个二次函数的图象与抛物线的形状相同、开口方向相同,且顶点坐标为,则这个函数的表达式是______________________.
12.如图,已知三边的长分别为5,12,13,那么的内切圆的半径为____.
第12题图
13.如图,一块矩形土地由篱笆围着,并且由一条与边平行的篱笆分开.已知篱笆的总长为(篱笆的厚度忽略不计),当____时,矩形土地的面积最大.
第13题图
14.如图,四边形内接于.若 ,则的度数为__________.
第14题图
15.如图,在中, ,,,为的中点,以点为圆心,长为半径作半圆,交于点,则图中阴影部分的面积是____________.
第15题图
16.如图,在平面直角坐标系中,点为坐标原点,正方形的顶点在轴的负半轴上,点在轴的正半轴上,经过点,的抛物线的顶点为.若为等腰直角三角形,则的值为________.
第16题图
17.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点,所在圆的圆心恰好是的内心,若,则花窗的周长(图中实线部分的长度)为______.(结果保留)
第17题图
18.如图,在中,,,则的外接圆的半径是________.
第18题图
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(6分)已知二次函数的表达式为.
(1) 此二次函数的顶点坐标为______________,与轴的交点坐标为____________和____________,与轴的交点坐标为____________;
(2) 如图,在平面直角坐标系中,画出这个二次函数的图象.
20.(6分)如图,点,的坐标分别为,,将绕点按逆时针方向旋转 得到.
(1) 在平面直角坐标系中画出;
(2) 点的坐标为____________;
(3) 求在旋转过程中,点所经过的路径的长度.
21.(8分)如图,已知在中,,与相交于点,连接,,.求证:
(1) ;
(2) 四边形为菱形.
22.(8分)已知二次函数.
(1) 当,时,
① 求该函数图象的顶点坐标;
② 当时,求的取值范围.
(2) 当时,的最大值为2;当时,的最大值为3,求二次函数的表达式.
23.(9分)某商场购进甲、乙两种商品共100箱,全部售完后,甲种商品共盈利900元,乙种商品共盈利400元,甲种商品比乙种商品每箱多盈利5元.
(1) 求甲、乙两种商品每箱各盈利多少元?
(2) 甲、乙两种商品全部售完后,该商场又购进一批甲商品,在原来每箱盈利不变的前提下,平均每天可卖出100箱.若调整价格,甲种商品每箱降价1元,则平均每天可多卖出20箱.那么当甲种商品每箱降价多少元时,该商场销售利润最大?最大利润是多少?
24.(9分)如图,已知抛物线关于轴对称,与轴交于,两点,点的坐标为,且抛物线经过点.
(1) 求抛物线的表达式;
(2) 已知点在轴上,在抛物线上是否存在点,使以,,,为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
25.(10分)如图,是的直径,于点,连接交于点,弦,弦于点.
(1) 求证:是的中点;
(2) 求证:是的切线;
(3) 若,的半径为5,求的长.
26.(10分)综合与实践
【问题提出】
(1) 如图①,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点,仅从射门角度大小考虑,甲是自己射门好,还是迅速将球回传给乙,让乙射门好?假设球员对球门的视角越大,足球越容易被踢进.请结合你所学知识,求证:.
【数学理解】
德国数学家米勒曾提出最大视角问题,对该问题的一般描述是:如图②,已知点,是的边上的两个定点,是边上的一个动点,当且仅当的外接圆与边相切于点时,最大,人们称这一命题为“米勒定理”.
【问题解决】
如图③,已知点,的坐标分别是,,是轴正半轴上的一动点,当的外接圆与轴相切于点时,最大,当最大时,求点的坐标.
期中质量评估
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.D 2.D 3.A 4.B 5.C 6.C 7.B 8.B 9.B 10.C
二、填空题(本题共8个小题,每小题3分,共24分)
11.
12.2
13.150
14.
15.
16.
17.
18.
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(1) ; ; ;
(2) 解:画出二次函数的图象如答图.
第19题答图
20.(1) 解:画出如答图.
第20题答图
(2)
(3) 的长为 .
21.(1) 证明:如答图,连接.
第21题答图
,,
.
(2) 如答图,设与相交于点.
,.
,,
.
又,
,
,
四边形为平行四边形.
又, 四边形为菱形.
22.(1) ① 解:,,
,
该函数图象的顶点坐标为.
② ,
当时,随的增大而增大;当时,随的增大而减小,
当时,有最大值7.
,
当时,有最小值,
当时,.
(2) 时,的最大值为2;时,的最大值为3,
抛物线的对称轴直线在轴的右侧,
.
抛物线开口向下,当时,的最大值为2,
.
又,
.
,.
二次函数的表达式为.
23.(1) 解:设甲种商品每箱盈利元,则乙种商品每箱盈利元.
由题意,得,
解得或(舍去).
经检验,是原分式方程的解,且符合实际,
(元).
答:甲种商品每箱盈利15元,乙种商品每箱盈利10元.
(2) 设甲种商品每箱降价元,利润为元,则每天可多卖出箱.
由题意,得.
,
当时,有最大值,最大值是2 000.
答:当甲种商品每箱降价5元时,该商场销售利润最大,最大利润是2 000元.
24.(1) 解: 抛物线关于轴对称,.
将点,点代入,
得解得
抛物线的表达式为.
(2) 存在点,使以,,,为顶点的四边形是平行四边形.
当时,.解得,.
设,.
当为平行四边形的对角线时,,即.
解得,此时;
当为平行四边形的对角线时,,即.
解得,此时;
当为平行四边形的对角线时,,即.
解得,此时.
综上所述,点的坐标为或或.
25.(1) 证明:如答图,连接.
第25题答图
,
,.
,,
,,
即是的中点.
(2) 证明:在和中,
,
.
, ,
,.
是的半径,是的切线.
(3) 解:,,,
.
,,.
设,则.
又的半径为5,.
,,
解得,(不合题意,舍去),
.
26.(1) 证明:,是所对的圆周角,
,
,
.
(2) 解:如答图,连接,过点作交轴于点,连接,
第26题答图
, ,
与轴相切于点,轴,
,
四边形是矩形,
,.
,,,
,,
,
点的坐标为.
[时间:120分钟 分值:120分]
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,属于二次函数的是( )
A. B.
C. D.
2.关于二次函数的图象,下列说法正确的是( )
A.开口向上 B.顶点坐标为
C.与轴交点为 D.对称轴为直线
3.在平面直角坐标系中,将抛物线先向左平移2个单位,再向上平移3个单位,则平移后抛物线的函数表达式是( )
A. B.
C. D.
4.在平面直角坐标系中,的直径为10.若圆心为坐标原点,则点与的位置关系是( )
A.点在上 B.点在外
C.点在内 D.无法确定
5.已知正六边形内接于,若的直径为2,则该正六边形的周长是( )
A.12 B. C.6 D.
6.如图,抛物线与轴交于,两点,与轴交于点,连接,,则的面积为( )
第6题图
A.1 B.2 C.4 D.8
7.如图,是的直径,与相切于点,交于点.若 ,则的度数为( )
第7题图
A. B. C. D.
8.如图,已知线段是的直径,弦于点.若,,则的长为( )
第8题图
A. B. C. D.5
9.已知,是抛物线是常数,上的两点,现有以下四个结论:①该抛物线的对称轴是直线;②点在抛物线上;③若,则;④若,则.其中结论正确的个数为( )
A.1 B.2 C.3 D.4
10.如图,在以为直径的中,为上的一点,,弦于点,弦交于点,交于点.若是的中点,则的度数为( )
A. B. C. D.
二、填空题(本题共8个小题,每小题3分,共24分)
11.一个二次函数的图象与抛物线的形状相同、开口方向相同,且顶点坐标为,则这个函数的表达式是______________________.
12.如图,已知三边的长分别为5,12,13,那么的内切圆的半径为____.
第12题图
13.如图,一块矩形土地由篱笆围着,并且由一条与边平行的篱笆分开.已知篱笆的总长为(篱笆的厚度忽略不计),当____时,矩形土地的面积最大.
第13题图
14.如图,四边形内接于.若 ,则的度数为__________.
第14题图
15.如图,在中, ,,,为的中点,以点为圆心,长为半径作半圆,交于点,则图中阴影部分的面积是____________.
第15题图
16.如图,在平面直角坐标系中,点为坐标原点,正方形的顶点在轴的负半轴上,点在轴的正半轴上,经过点,的抛物线的顶点为.若为等腰直角三角形,则的值为________.
第16题图
17.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点,所在圆的圆心恰好是的内心,若,则花窗的周长(图中实线部分的长度)为______.(结果保留)
第17题图
18.如图,在中,,,则的外接圆的半径是________.
第18题图
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(6分)已知二次函数的表达式为.
(1) 此二次函数的顶点坐标为______________,与轴的交点坐标为____________和____________,与轴的交点坐标为____________;
(2) 如图,在平面直角坐标系中,画出这个二次函数的图象.
20.(6分)如图,点,的坐标分别为,,将绕点按逆时针方向旋转 得到.
(1) 在平面直角坐标系中画出;
(2) 点的坐标为____________;
(3) 求在旋转过程中,点所经过的路径的长度.
21.(8分)如图,已知在中,,与相交于点,连接,,.求证:
(1) ;
(2) 四边形为菱形.
22.(8分)已知二次函数.
(1) 当,时,
① 求该函数图象的顶点坐标;
② 当时,求的取值范围.
(2) 当时,的最大值为2;当时,的最大值为3,求二次函数的表达式.
23.(9分)某商场购进甲、乙两种商品共100箱,全部售完后,甲种商品共盈利900元,乙种商品共盈利400元,甲种商品比乙种商品每箱多盈利5元.
(1) 求甲、乙两种商品每箱各盈利多少元?
(2) 甲、乙两种商品全部售完后,该商场又购进一批甲商品,在原来每箱盈利不变的前提下,平均每天可卖出100箱.若调整价格,甲种商品每箱降价1元,则平均每天可多卖出20箱.那么当甲种商品每箱降价多少元时,该商场销售利润最大?最大利润是多少?
24.(9分)如图,已知抛物线关于轴对称,与轴交于,两点,点的坐标为,且抛物线经过点.
(1) 求抛物线的表达式;
(2) 已知点在轴上,在抛物线上是否存在点,使以,,,为顶点的四边形是平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
25.(10分)如图,是的直径,于点,连接交于点,弦,弦于点.
(1) 求证:是的中点;
(2) 求证:是的切线;
(3) 若,的半径为5,求的长.
26.(10分)综合与实践
【问题提出】
(1) 如图①,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点,仅从射门角度大小考虑,甲是自己射门好,还是迅速将球回传给乙,让乙射门好?假设球员对球门的视角越大,足球越容易被踢进.请结合你所学知识,求证:.
【数学理解】
德国数学家米勒曾提出最大视角问题,对该问题的一般描述是:如图②,已知点,是的边上的两个定点,是边上的一个动点,当且仅当的外接圆与边相切于点时,最大,人们称这一命题为“米勒定理”.
【问题解决】
如图③,已知点,的坐标分别是,,是轴正半轴上的一动点,当的外接圆与轴相切于点时,最大,当最大时,求点的坐标.
期中质量评估
一、选择题(本题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.D 2.D 3.A 4.B 5.C 6.C 7.B 8.B 9.B 10.C
二、填空题(本题共8个小题,每小题3分,共24分)
11.
12.2
13.150
14.
15.
16.
17.
18.
三、解答题(本题共8个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
19.(1) ; ; ;
(2) 解:画出二次函数的图象如答图.
第19题答图
20.(1) 解:画出如答图.
第20题答图
(2)
(3) 的长为 .
21.(1) 证明:如答图,连接.
第21题答图
,,
.
(2) 如答图,设与相交于点.
,.
,,
.
又,
,
,
四边形为平行四边形.
又, 四边形为菱形.
22.(1) ① 解:,,
,
该函数图象的顶点坐标为.
② ,
当时,随的增大而增大;当时,随的增大而减小,
当时,有最大值7.
,
当时,有最小值,
当时,.
(2) 时,的最大值为2;时,的最大值为3,
抛物线的对称轴直线在轴的右侧,
.
抛物线开口向下,当时,的最大值为2,
.
又,
.
,.
二次函数的表达式为.
23.(1) 解:设甲种商品每箱盈利元,则乙种商品每箱盈利元.
由题意,得,
解得或(舍去).
经检验,是原分式方程的解,且符合实际,
(元).
答:甲种商品每箱盈利15元,乙种商品每箱盈利10元.
(2) 设甲种商品每箱降价元,利润为元,则每天可多卖出箱.
由题意,得.
,
当时,有最大值,最大值是2 000.
答:当甲种商品每箱降价5元时,该商场销售利润最大,最大利润是2 000元.
24.(1) 解: 抛物线关于轴对称,.
将点,点代入,
得解得
抛物线的表达式为.
(2) 存在点,使以,,,为顶点的四边形是平行四边形.
当时,.解得,.
设,.
当为平行四边形的对角线时,,即.
解得,此时;
当为平行四边形的对角线时,,即.
解得,此时;
当为平行四边形的对角线时,,即.
解得,此时.
综上所述,点的坐标为或或.
25.(1) 证明:如答图,连接.
第25题答图
,
,.
,,
,,
即是的中点.
(2) 证明:在和中,
,
.
, ,
,.
是的半径,是的切线.
(3) 解:,,,
.
,,.
设,则.
又的半径为5,.
,,
解得,(不合题意,舍去),
.
26.(1) 证明:,是所对的圆周角,
,
,
.
(2) 解:如答图,连接,过点作交轴于点,连接,
第26题答图
, ,
与轴相切于点,轴,
,
四边形是矩形,
,.
,,,
,,
,
点的坐标为.
同课章节目录
