平行四边形
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
江苏省淮北中学八年级单元测试卷
平行四边形(一)
一、填空题(每小题4分,本题满分20分)
1.平行四边形ABCD周长为20,边AB的长度比BC的长度大2,则DA的长度为 .
2.平行四边形ABCD中,∠B-∠A=40,则∠C= ,∠D= .
3.写出菱形所特有的,有别于一般平行四边形的特征: , , .
4.矩形ABCD的对角线交点为O,△OBA为一个等边三角形,已知此矩形的短边长2cm,则矩形的对角线长为 .
5.如图,E是梯形ABCD对角线的交点,则图中面积相等的三角形共有 对.
二、选择题(每小题5分,本题满分25分)
6.下列条件中不能判断一个四边形是平行四边形的是( ).
(A)两组邻角分别互补 (B)四个内角皆为直角
(C)一组对边平行且相等 (D)对角线互相平分.
7.下列图形中,是中心对称图形,但没有对称轴的是( ).
(A)正方形 (B)菱形 (C)矩形 (D)非菱形、非矩形的平行四边形
8.两组对角分别相等,且互补的四边形一定是( ).
(A)正方形 (B)菱形 (C)矩形 (D)非菱形、非矩形的平行四边形
9.一个等腰梯形的上底和腰的长都是1,下底的长为2,将这个梯形按下图的方式拼接在一起: 共有八个这样的梯形,则由它们拼接成的图形周长为( ).
(A)14 (B)26 (C)32 (D)36
10.如图,有九个点在平面上排成3×3的方阵,以这些点为顶点的正方形有( ).
(A)4个 (B)5个 (C)6个 (D)8个
三、解答题
11.我们知道平行四边形和直线都是中心对称图形,利用这一特征说明下面的事实:
设E是平行四边行ABCD对角线的交点,一直线经过E和平行四边形一组对边交于点P、Q,如图,则EP和EQ的长相等(本题满分8分).
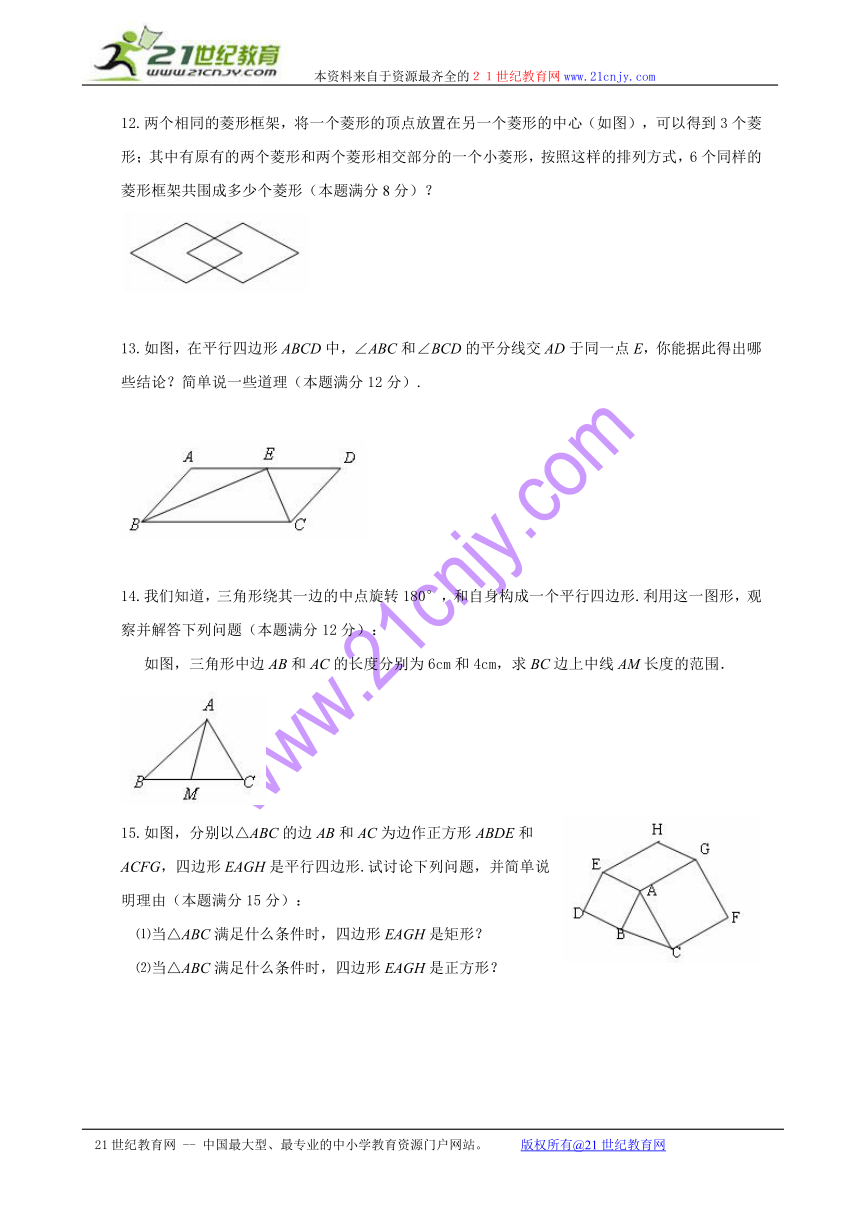
12.两个相同的菱形框架,将一个菱形的顶点放置在另一个菱形的中心(如图),可以得到3个菱形;其中有原有的两个菱形和两个菱形相交部分的一个小菱形,按照这样的排列方式,6个同样的菱形框架共围成多少个菱形(本题满分8分)?
13.如图,在平行四边形ABCD中,∠ABC和∠BCD的平分线交AD于同一点E,你能据此得出哪些结论?简单说一些道理(本题满分12分).
14.我们知道,三角形绕其一边的中点旋转180°,和自身构成一个平行四边形.利用这一图形,观察并解答下列问题(本题满分12分):
如图,三角形中边AB和AC的长度分别为6cm和4cm,求BC边上中线AM长度的范围.
15.如图,分别以△ABC的边AB和AC为边作正方形ABDE和ACFG,四边形EAGH是平行四边形.试讨论下列问题,并简单说明理由(本题满分15分):
⑴当△ABC满足什么条件时,四边形EAGH是矩形?
⑵当△ABC满足什么条件时,四边形EAGH是正方形?
江苏省淮北中学八年级单元测试卷
平行四边形(二)
一、填空题(每小题4分,本题满分20分)
1.在等腰梯形中,有一个内角是72°,则其余三个角的度数分别为 .
2.在平行四边形ABCD中,∠A的大小是∠B的三倍,则∠C= .
3.一个菱形的对角线长度分别为4cm和8cm,则这个菱形的面积为 .
4.矩形ABCD的对角线交于点E,如果已知矩形对角线的长度是边AB长度的两倍,那么∠BCE= .
5.平行四边形ABCD中,AB的中点为P、BC的中点为Q,连结PQ和QC,得到图中阴影部分的面积为16cm2,则图中空白部分的面积为 .
二、选择题(每小题5分,本题满分25分)
6.下列条件中能判断一个四边形为菱形的是 ( ).
(A)不是矩形的平行四边形 (B)对角线互相垂直
(C)有一条对角线垂直平分另一条对角线 (D)对角线互相垂直的矩形
7.已知平行四边形的三个顶点,则第四个顶点的可能位置有 ( ).
(A)1个 (B)2个 (C)3个 (D)4个
8.如图,四边形CDEF旋转后与正方形ABCD重合,那么,旋转中心可以取的位置有 ( ).
(A)1个 (B)2个 (C)3个 (D)4个
9.如图,有九个点在平面上形成3×3的方阵,以这些点为顶点的梯形有( ).
(A)20个 (B)28个 (C)32个 (D)36个
10.设平面内有一个等边三角形,P是等边三角形所在平面内的一点,P和三角形的任意两个顶点构成一个等腰三角形,则P的位置有( ).
(A)4个 (B)7个 (C)10个 (D)13个
三、解答题
11.直角三角形绕其斜边的中点旋转180°,和自身构成一个矩形.试用这个方法观察并说明:直角三角形斜边上的中线长度和斜边长之间的关系(本题满分8分).
12.两个相同的正方形A和B,A的一个顶点O位于B的对角线交点,将A以O为中心逆时针旋转,这时,A和B重叠部分(阴影区)的面积将怎样变化(本题满分8分)?
13.我们在画四边形时有时借助于“三角形奠基法”:例如需要作出一个下底长为7,上底长为3,腰长分别为5和6的梯形,考虑到过梯形上底的一个端点作另一腰的平行线,能把这个梯形分成两块:一块为三角形,另一块是平行四边形,在本题中,三角形的边长为5、6和(下底长-上底长)=4,首先作出这个三角形;然后把长度为4的线段向任一个方向延长3个单位;最后再作出以这条延长线段和三角形的一条边作为邻边的平行四边形,就得到满足要求的梯形.
根据上面的描述,试画出一个平行四边形,使它的一条边长2cm,两条对角线长分别为3cm和2cm(本题满分12分).
14.小新在工艺课上将两张等宽的长方形纸条叠在一起,小华发现这两张纸的重叠部分(图中阴影部分)构成了一个菱形,试了几次都是这样,小新却说这只是偶然的. 你的看法怎样?
说一说你的道理(本题满分12分).
15.梯形ABCD中AD∥BC,AB⊥BC.点P从A出发以1厘米/秒的速度沿AD移动,点Q同时从C出发以2厘米/秒的速度沿CB移动.若AD=18厘米,BC=24厘米,试讨论(本题满分15分):
(1)运动多少时间后四边形ABQP是矩形?
(2)运动多少时间后四边形DCQP是等腰梯形?
(3)运动多少时间后四边形DCQP的面积最大?
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
江苏省淮北中学八年级单元测试卷
平行四边形(一)
一、填空题(每小题4分,本题满分20分)
1.平行四边形ABCD周长为20,边AB的长度比BC的长度大2,则DA的长度为 .
2.平行四边形ABCD中,∠B-∠A=40,则∠C= ,∠D= .
3.写出菱形所特有的,有别于一般平行四边形的特征: , , .
4.矩形ABCD的对角线交点为O,△OBA为一个等边三角形,已知此矩形的短边长2cm,则矩形的对角线长为 .
5.如图,E是梯形ABCD对角线的交点,则图中面积相等的三角形共有 对.
二、选择题(每小题5分,本题满分25分)
6.下列条件中不能判断一个四边形是平行四边形的是( ).
(A)两组邻角分别互补 (B)四个内角皆为直角
(C)一组对边平行且相等 (D)对角线互相平分.
7.下列图形中,是中心对称图形,但没有对称轴的是( ).
(A)正方形 (B)菱形 (C)矩形 (D)非菱形、非矩形的平行四边形
8.两组对角分别相等,且互补的四边形一定是( ).
(A)正方形 (B)菱形 (C)矩形 (D)非菱形、非矩形的平行四边形
9.一个等腰梯形的上底和腰的长都是1,下底的长为2,将这个梯形按下图的方式拼接在一起: 共有八个这样的梯形,则由它们拼接成的图形周长为( ).
(A)14 (B)26 (C)32 (D)36
10.如图,有九个点在平面上排成3×3的方阵,以这些点为顶点的正方形有( ).
(A)4个 (B)5个 (C)6个 (D)8个
三、解答题
11.我们知道平行四边形和直线都是中心对称图形,利用这一特征说明下面的事实:
设E是平行四边行ABCD对角线的交点,一直线经过E和平行四边形一组对边交于点P、Q,如图,则EP和EQ的长相等(本题满分8分).
12.两个相同的菱形框架,将一个菱形的顶点放置在另一个菱形的中心(如图),可以得到3个菱形;其中有原有的两个菱形和两个菱形相交部分的一个小菱形,按照这样的排列方式,6个同样的菱形框架共围成多少个菱形(本题满分8分)?
13.如图,在平行四边形ABCD中,∠ABC和∠BCD的平分线交AD于同一点E,你能据此得出哪些结论?简单说一些道理(本题满分12分).
14.我们知道,三角形绕其一边的中点旋转180°,和自身构成一个平行四边形.利用这一图形,观察并解答下列问题(本题满分12分):
如图,三角形中边AB和AC的长度分别为6cm和4cm,求BC边上中线AM长度的范围.
15.如图,分别以△ABC的边AB和AC为边作正方形ABDE和ACFG,四边形EAGH是平行四边形.试讨论下列问题,并简单说明理由(本题满分15分):
⑴当△ABC满足什么条件时,四边形EAGH是矩形?
⑵当△ABC满足什么条件时,四边形EAGH是正方形?
江苏省淮北中学八年级单元测试卷
平行四边形(二)
一、填空题(每小题4分,本题满分20分)
1.在等腰梯形中,有一个内角是72°,则其余三个角的度数分别为 .
2.在平行四边形ABCD中,∠A的大小是∠B的三倍,则∠C= .
3.一个菱形的对角线长度分别为4cm和8cm,则这个菱形的面积为 .
4.矩形ABCD的对角线交于点E,如果已知矩形对角线的长度是边AB长度的两倍,那么∠BCE= .
5.平行四边形ABCD中,AB的中点为P、BC的中点为Q,连结PQ和QC,得到图中阴影部分的面积为16cm2,则图中空白部分的面积为 .
二、选择题(每小题5分,本题满分25分)
6.下列条件中能判断一个四边形为菱形的是 ( ).
(A)不是矩形的平行四边形 (B)对角线互相垂直
(C)有一条对角线垂直平分另一条对角线 (D)对角线互相垂直的矩形
7.已知平行四边形的三个顶点,则第四个顶点的可能位置有 ( ).
(A)1个 (B)2个 (C)3个 (D)4个
8.如图,四边形CDEF旋转后与正方形ABCD重合,那么,旋转中心可以取的位置有 ( ).
(A)1个 (B)2个 (C)3个 (D)4个
9.如图,有九个点在平面上形成3×3的方阵,以这些点为顶点的梯形有( ).
(A)20个 (B)28个 (C)32个 (D)36个
10.设平面内有一个等边三角形,P是等边三角形所在平面内的一点,P和三角形的任意两个顶点构成一个等腰三角形,则P的位置有( ).
(A)4个 (B)7个 (C)10个 (D)13个
三、解答题
11.直角三角形绕其斜边的中点旋转180°,和自身构成一个矩形.试用这个方法观察并说明:直角三角形斜边上的中线长度和斜边长之间的关系(本题满分8分).
12.两个相同的正方形A和B,A的一个顶点O位于B的对角线交点,将A以O为中心逆时针旋转,这时,A和B重叠部分(阴影区)的面积将怎样变化(本题满分8分)?
13.我们在画四边形时有时借助于“三角形奠基法”:例如需要作出一个下底长为7,上底长为3,腰长分别为5和6的梯形,考虑到过梯形上底的一个端点作另一腰的平行线,能把这个梯形分成两块:一块为三角形,另一块是平行四边形,在本题中,三角形的边长为5、6和(下底长-上底长)=4,首先作出这个三角形;然后把长度为4的线段向任一个方向延长3个单位;最后再作出以这条延长线段和三角形的一条边作为邻边的平行四边形,就得到满足要求的梯形.
根据上面的描述,试画出一个平行四边形,使它的一条边长2cm,两条对角线长分别为3cm和2cm(本题满分12分).
14.小新在工艺课上将两张等宽的长方形纸条叠在一起,小华发现这两张纸的重叠部分(图中阴影部分)构成了一个菱形,试了几次都是这样,小新却说这只是偶然的. 你的看法怎样?
说一说你的道理(本题满分12分).
15.梯形ABCD中AD∥BC,AB⊥BC.点P从A出发以1厘米/秒的速度沿AD移动,点Q同时从C出发以2厘米/秒的速度沿CB移动.若AD=18厘米,BC=24厘米,试讨论(本题满分15分):
(1)运动多少时间后四边形ABQP是矩形?
(2)运动多少时间后四边形DCQP是等腰梯形?
(3)运动多少时间后四边形DCQP的面积最大?
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
