2024-2025学年初中数学人教版九年级下册 29.2三视图(课时2) 课件(共31张PPT)
文档属性
| 名称 | 2024-2025学年初中数学人教版九年级下册 29.2三视图(课时2) 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 22:32:37 | ||
图片预览







文档简介
(共31张PPT)
29.2 三视图(课时2)
第二十九章 投影与视图
素养目标
1.能够根据物体的三视图描述出几何体的基本形状或实物原型;
2.能够通过简单的三视图还原立体图形本身,并解决面积、体积问题;
3.经历由“三视图”想象出立体几何图形本身的过程,培养学生分析问题、解决问题的能力
重点
重难点
新知导入
上节课我们学习了画立体图形的三视图,你能准确画出下面几个常见的几何体的三视图吗?
反之,已知一个立体图形的三视图,如何还原立体图形呢?
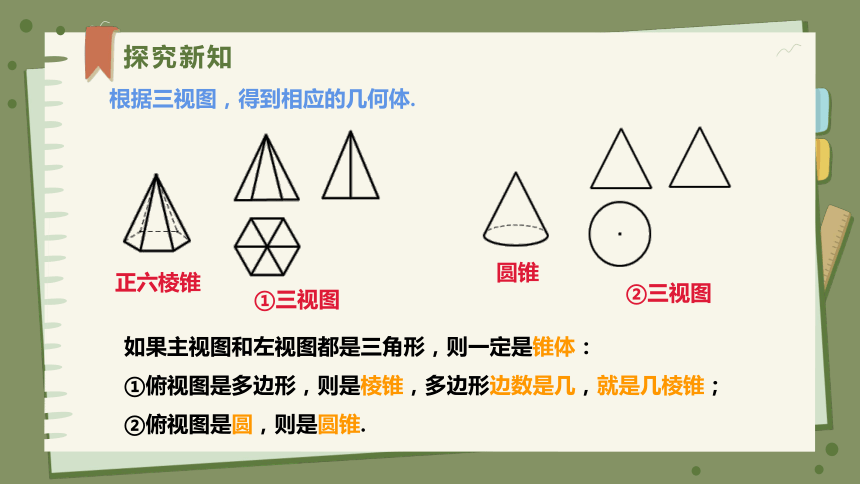
探究新知
根据三视图,得到相应的几何体.
①三视图
②三视图
如果主视图和左视图都是三角形,则一定是锥体:
①俯视图是多边形,则是棱锥,多边形边数是几,就是几棱锥;
②俯视图是圆,则是圆锥.
圆锥
正六棱锥
探究新知
根据三视图,得到相应的几何体.
①三视图
②三视图
正六棱柱
圆柱
如果主视图和左视图都是矩形,则一定是柱体:
①俯视图是多边形,则是棱柱,多边形边数是几,就是几棱柱;
②俯视图是圆,则是圆柱.
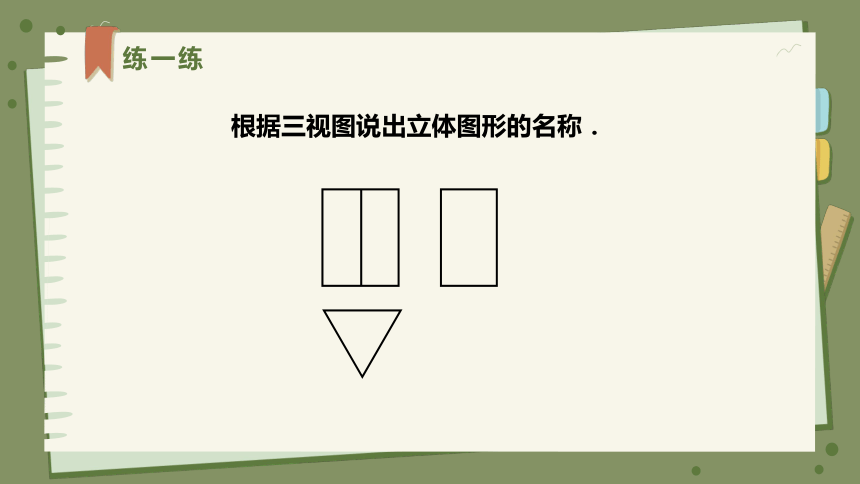
练一练
根据三视图说出立体图形的名称.
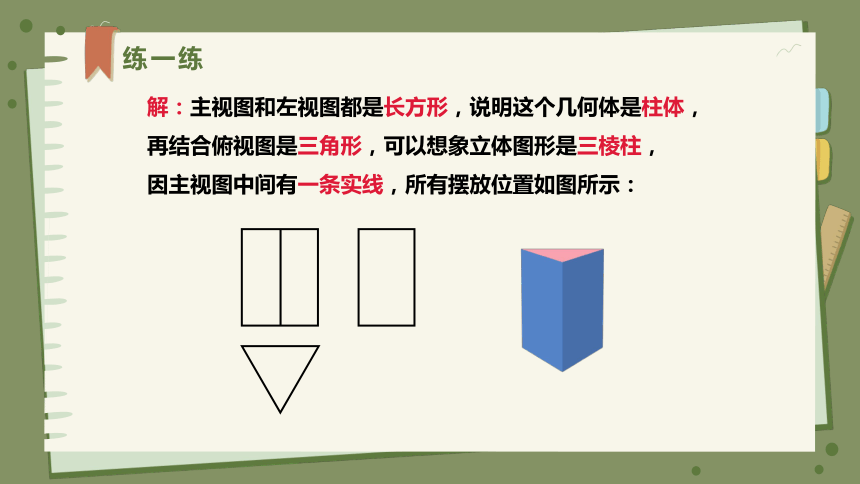
练一练
解:主视图和左视图都是长方形,说明这个几何体是柱体,
再结合俯视图是三角形,可以想象立体图形是三棱柱,
因主视图中间有一条实线,所有摆放位置如图所示:
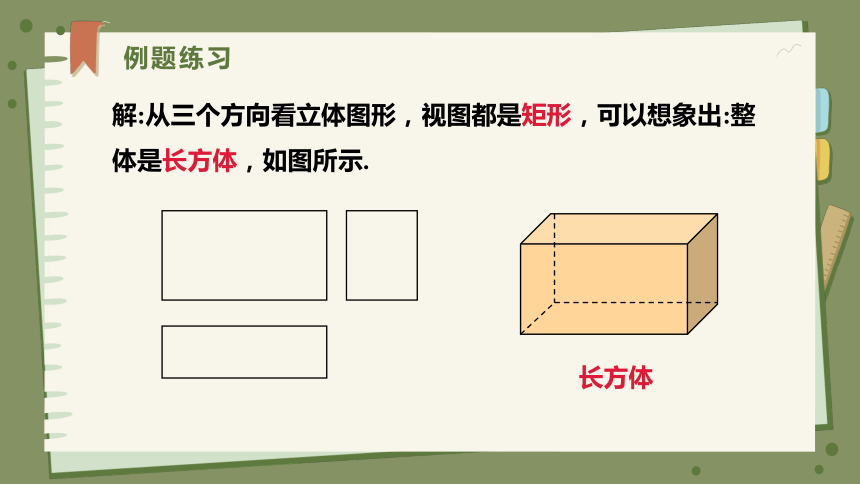
例题练习
如图,分别根据三视图说出立体图形的名称.
例题练习
解:从三个方向看立体图形,视图都是矩形,可以想象出:整体是长方体,如图所示.
长方体
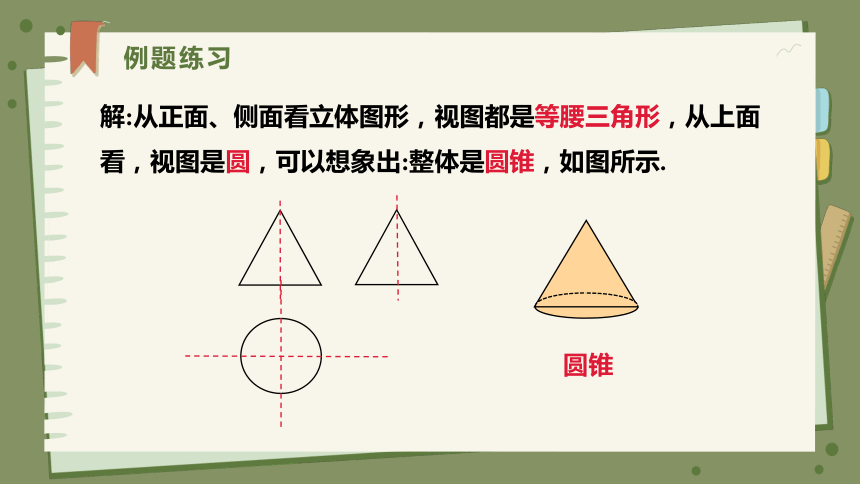
例题练习
解:从正面、侧面看立体图形,视图都是等腰三角形,从上面看,视图是圆,可以想象出:整体是圆锥,如图所示.
圆锥
例题练习
根据物体的三视图,描述物体的形状.
例题练习
由主视图可知,物体的正面是正五边形 ,由俯视图知,由上向下看物体有两个面的视图是矩形,它们的交线是一条棱 (实线),可见到,另有两条棱被遮挡(虚线);由左视图知,物体的左侧有两个面的视图是矩形,它们的交线是一条棱(实线) ,可见到.综合各视图可知,该物体是正五棱柱形状的.
探究新知
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就是立体图形的展开图.
探究新知
根据下列几何体的三视图,画出它们的展开图.
圆柱
长方体
例题练习
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
100mm
50mm
50mm
100mm
主视图
左视图
俯视图
【分析】在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
例题练习
解:由三视图可知,密封罐的现状是正六棱柱.
由三视图可知,密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,右图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积:
归纳总结
由三视图求立体图形的面积的方法:
(1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
(2)将立体图形展开成一个平面图形(展开图),观察它的组成部分.
(3)最后根据已知数据,求出展开图的面积.
A
A
B
D
136π
长方体
圆锥
圆柱
小结
三种图形的转化:
三视图
立体图
展开图
谢谢同学们的聆听
29.2 三视图(课时2)
第二十九章 投影与视图
素养目标
1.能够根据物体的三视图描述出几何体的基本形状或实物原型;
2.能够通过简单的三视图还原立体图形本身,并解决面积、体积问题;
3.经历由“三视图”想象出立体几何图形本身的过程,培养学生分析问题、解决问题的能力
重点
重难点
新知导入
上节课我们学习了画立体图形的三视图,你能准确画出下面几个常见的几何体的三视图吗?
反之,已知一个立体图形的三视图,如何还原立体图形呢?
探究新知
根据三视图,得到相应的几何体.
①三视图
②三视图
如果主视图和左视图都是三角形,则一定是锥体:
①俯视图是多边形,则是棱锥,多边形边数是几,就是几棱锥;
②俯视图是圆,则是圆锥.
圆锥
正六棱锥
探究新知
根据三视图,得到相应的几何体.
①三视图
②三视图
正六棱柱
圆柱
如果主视图和左视图都是矩形,则一定是柱体:
①俯视图是多边形,则是棱柱,多边形边数是几,就是几棱柱;
②俯视图是圆,则是圆柱.
练一练
根据三视图说出立体图形的名称.
练一练
解:主视图和左视图都是长方形,说明这个几何体是柱体,
再结合俯视图是三角形,可以想象立体图形是三棱柱,
因主视图中间有一条实线,所有摆放位置如图所示:
例题练习
如图,分别根据三视图说出立体图形的名称.
例题练习
解:从三个方向看立体图形,视图都是矩形,可以想象出:整体是长方体,如图所示.
长方体
例题练习
解:从正面、侧面看立体图形,视图都是等腰三角形,从上面看,视图是圆,可以想象出:整体是圆锥,如图所示.
圆锥
例题练习
根据物体的三视图,描述物体的形状.
例题练习
由主视图可知,物体的正面是正五边形 ,由俯视图知,由上向下看物体有两个面的视图是矩形,它们的交线是一条棱 (实线),可见到,另有两条棱被遮挡(虚线);由左视图知,物体的左侧有两个面的视图是矩形,它们的交线是一条棱(实线) ,可见到.综合各视图可知,该物体是正五棱柱形状的.
探究新知
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就是立体图形的展开图.
探究新知
根据下列几何体的三视图,画出它们的展开图.
圆柱
长方体
例题练习
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
100mm
50mm
50mm
100mm
主视图
左视图
俯视图
【分析】在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
例题练习
解:由三视图可知,密封罐的现状是正六棱柱.
由三视图可知,密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,右图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积:
归纳总结
由三视图求立体图形的面积的方法:
(1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
(2)将立体图形展开成一个平面图形(展开图),观察它的组成部分.
(3)最后根据已知数据,求出展开图的面积.
A
A
B
D
136π
长方体
圆锥
圆柱
小结
三种图形的转化:
三视图
立体图
展开图
谢谢同学们的聆听
