2024-2025学年人教版八年级上册 数学 第十二章 全等三角形 综合测试卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版八年级上册 数学 第十二章 全等三角形 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 874.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-28 00:00:00 | ||
图片预览

文档简介
第十二章综合测试卷
考试时间:120分钟 满分:120分
一、选择题
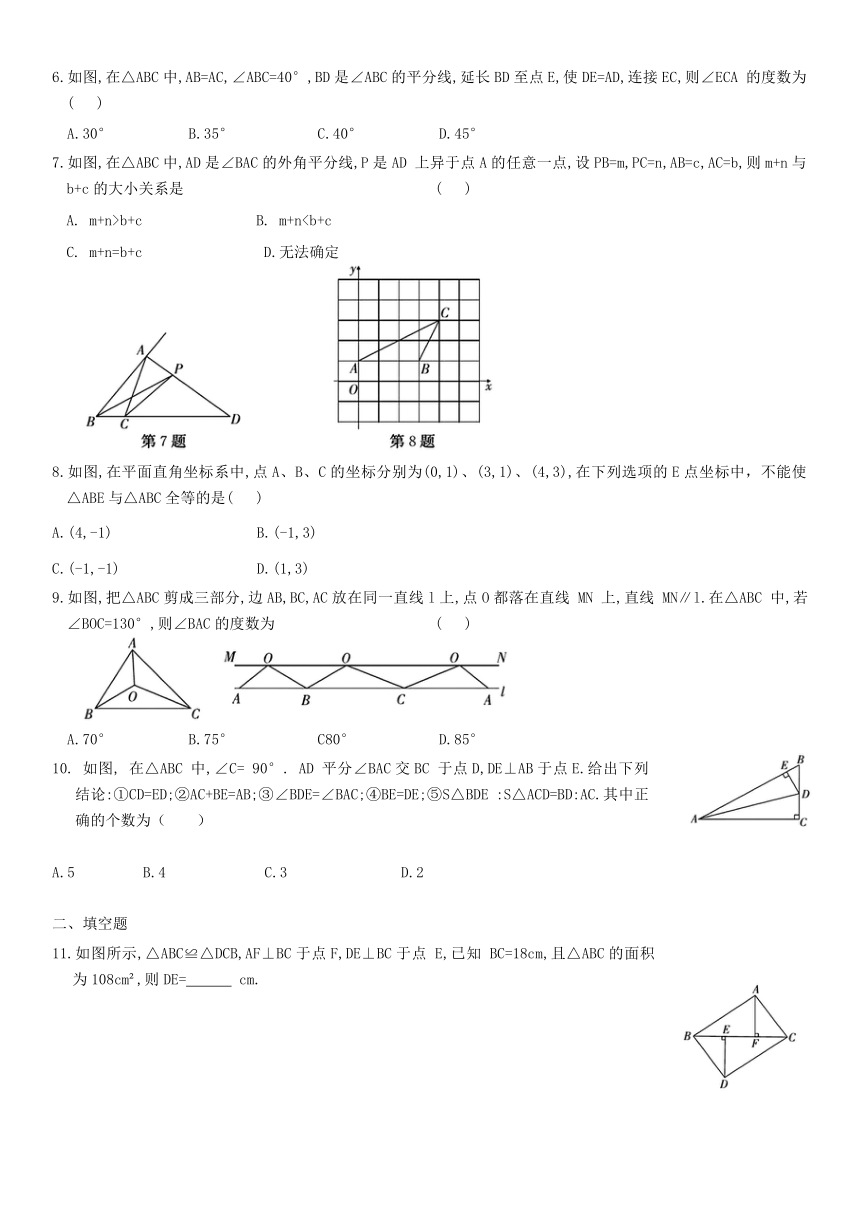
1.如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC=( )
A.27° B.30° C.54° D.55°
2.下列各组条件中,不能使两个直角三角形全等的是 ( )
A.一条直角边和它的对角分别相等
B.斜边和一条直角边分别相等
C.斜边和一锐角分别相等
D.两个锐角分别相等
3.已知∠AOB=60°,以O为圆心,任意长为半径作弧,分别交OA、OB于点M、N,分别以点M、N为圆心,大于 MN的长度为半径作弧,两弧在∠AOB 内交于点 P,以OP 为边作∠POC=15°,则∠BOC的度数为( )
A.15° B.45° C.15°或30° D.15°或45°
4.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是 ( )
A.24 B.30 C.36 D.42
5.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
6.如图,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使DE=AD,连接EC,则∠ECA 的度数为( )
A.30° B.35° C.40° D.45°
7.如图,在△ABC中,AD是∠BAC的外角平分线,P是AD 上异于点A的任意一点,设PB=m,PC=n,AB=c,AC=b,则m+n与b+c的大小关系是 ( )
A. m+n>b+c B. m+nC. m+n=b+c D.无法确定
8.如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(3,1)、(4,3),在下列选项的E点坐标中,不能使△ABE与△ABC全等的是( )
A.(4,-1) B.(-1,3)
C.(-1,-1) D.(1,3)
9.如图,把△ABC剪成三部分,边AB,BC,AC放在同一直线l上,点O都落在直线 MN 上,直线 MN∥l.在△ABC 中,若∠BOC=130°,则∠BAC的度数为 ( )
A.70° B.75° C80° D.85°
10. 如图, 在△ABC 中,∠C= 90°. AD 平分∠BAC交BC 于点D,DE⊥AB于点E.给出下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE :S△ACD=BD:AC.其中正确的个数为( )
A.5 B.4 C.3 D.2
二、填空题
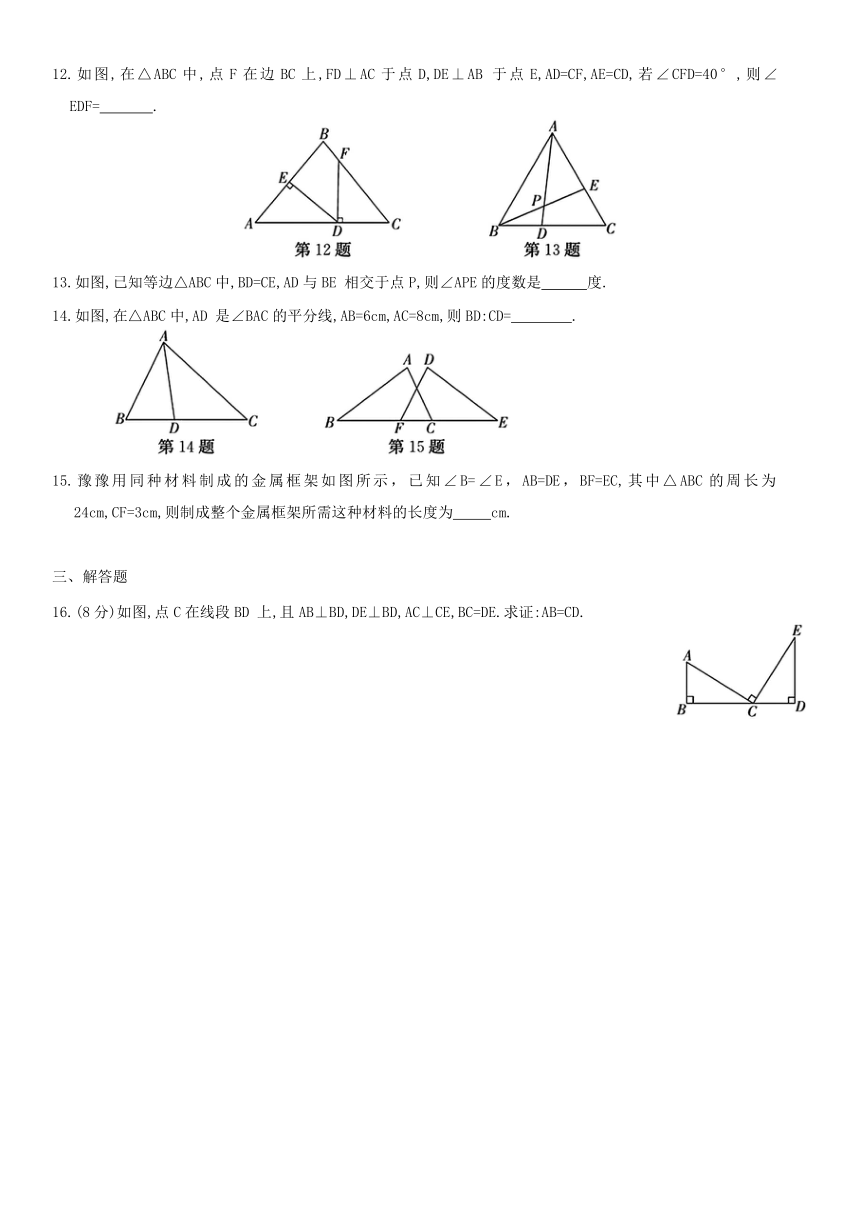
11.如图所示,△ABC≌△DCB,AF⊥BC于点F,DE⊥BC于点 E,已知 BC=18cm,且△ABC的面积为108cm ,则DE= cm.
12.如图,在△ABC中,点F在边BC上,FD⊥AC于点D,DE⊥AB 于点E,AD=CF,AE=CD,若∠CFD=40°,则∠EDF= .
13.如图,已知等边△ABC中,BD=CE,AD与BE 相交于点P,则∠APE的度数是 度.
14.如图,在△ABC中,AD 是∠BAC的平分线,AB=6cm,AC=8cm,则BD:CD= .
15.豫豫用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的长度为 cm.
三、解答题
16.(8分)如图,点C在线段BD 上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
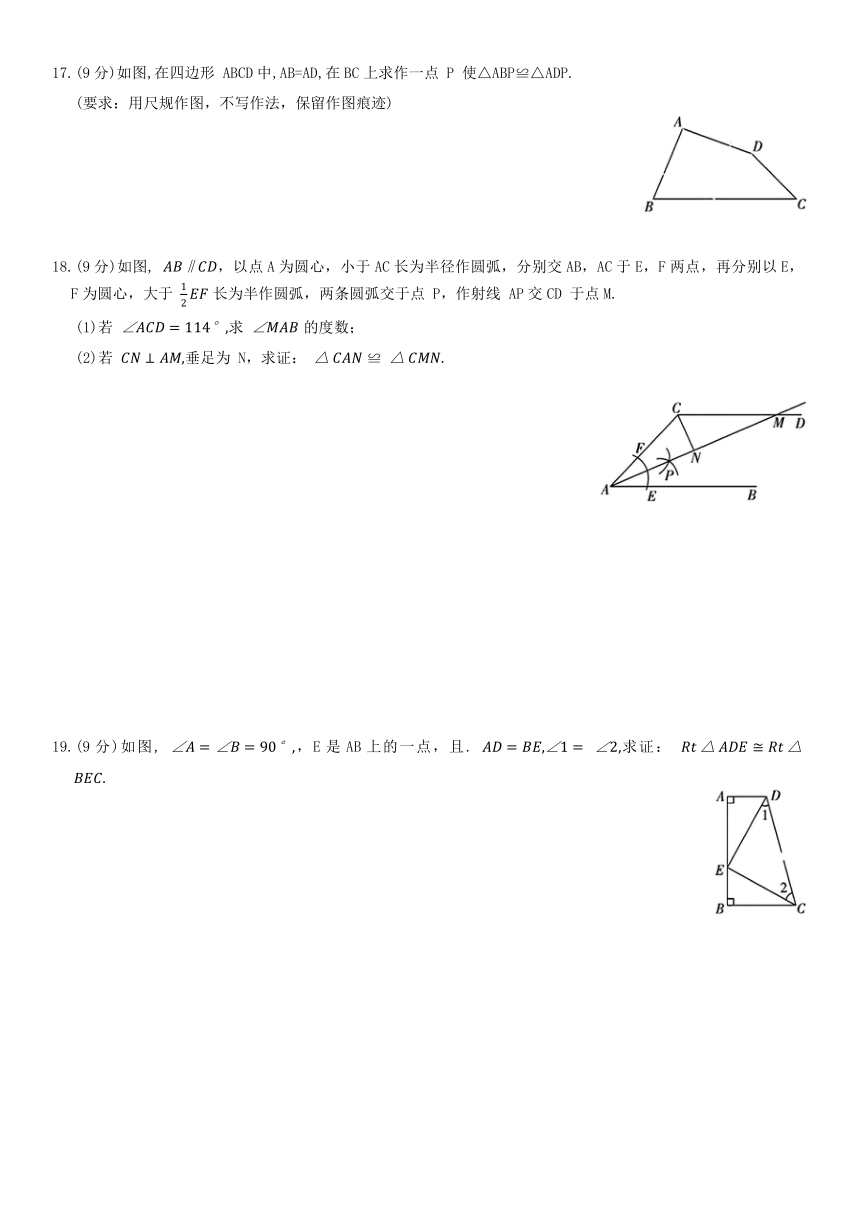
17.(9分)如图,在四边形 ABCD中,AB=AD,在BC上求作一点 P 使△ABP≌△ADP.
(要求:用尺规作图,不写作法,保留作图痕迹)
18.(9分)如图, ,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 长为半作圆弧,两条圆弧交于点 P,作射线 AP交CD 于点M.
(1)若 求 的度数;
(2)若 垂足为 N,求证: ≌
19.(9分)如图, ,E是AB上的一点,且. 求证:
20.(9分)如图,C,E分别为 的边BD,AB上的点,且 ,求∠B的度数.
21.(10分)如图,已知 的角平分线BM,CN 相交于点 P.
(1)AP是否平分 请说明理由.
(2)由此题你得到的结论是 .
22.(10 分)如图,在四边形ABCD 中, ,AC平分 ,过点 C作CE⊥AD,垂足为 E, ,求四边形ABCD的周长.
23.(11分)课外兴趣小组活动时,老师提出了如下问题:
如图(1), 中,若 ,求BC边上的中线AD 的取值范围.经过组内合作交流,小明得到了如下的解决方法:延长AD 到点E,使 请根据小明的方法思考:
(1)由已知和作图能得到 ≌ 的理由是 .
A. SSS B. SAS C. AAS D. HL
(2)求得AD的取值范围是 .
第十二章综合测试卷
选择题
1、C 2、D 3、D 4、C 5、C 6、C 7、A 8、D 9、C 10、C
二、填空题
11、12 12、50°13、60 14、3:4 15、45
三、解答题
16、证明:∵AB⊥BD,DE⊥BD, AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠E=90°,
∴∠ACB=∠E.在△ABC和△CDE 中, (ASA),
∴AB=CD.
17、解:点P 如图所示.
18、(1) 解: ∵ AB∥CD,
∴∠ACD +∠CAB=180°.
又∵∠ACD=114°,
∴∠CAB = 66°.
由 作法 知, AM 是∠CAB 的平分线,
∠CAB=33°.
证明:由作法可知,AN 平分∠CAB,
∴∠CAM=∠MAB.
∵AB∥CD,
∴∠MAB=∠CMA,
∴∠CAM=∠CMA.
又∵CN⊥AM,CN= CN.
∴∠CNA =∠CNM= 90°,
∴△CAN≌△CMN(AAS).
证明:过点E 作EF⊥CD 于点 F,则∠EFC=∠EFD=90°.
又∵∠1=∠2,EF=EF,
∴△EFD≌△EFC(AAS),
∴DE =CE.
∵∠A=∠B =90°,
∴ 在 Rt△ADE 和 Rt△BEC 中,
△BEC(HL).
20、解:如图,连接 AC. 在△AEC 和△ADC 中,
∴∠AEC=∠D=70°,
∴∠BEC=180°-70°=110°,
∵∠ECD=150°,
∴∠B=∠ECD-∠BEC=150°-110°=40°.
21、解:(1)AP 平分∠BAC.理由如下:如图,过点 P 作PQ⊥BC 于点Q ,
PK⊥AB 于点 K,PL⊥AC 于点 L,
∵△ABC 的角平分线BM,CN 相交于点P,
∴PK=PQ,PL=PQ,∴PK=PL,∴AP 平分∠BAC.
(2)三角形的三条角平分线相交于一点 .
22、解:如图,过 C点作CH⊥AB,交 AB 的延长线于点 H.
∵AC 平分∠BAD,CH⊥AH,CE⊥AD.
∴CH=CE.
∵∠BAD+∠BCD=180°,
∴∠ABC+∠D =180°.
∵∠ABC+∠HBC =180°,
∴∠HBC=∠D.
又∵∠H=∠CED=90°.
∴△HBC≌△EDC(AAS).
∴HB=DE,BC=CD=4. 在 Rt△ACH 和 Rt△ACE 中,AC=ACC,
∴Rt△ACH≌Rt△ACE(HL).
∴AH=AE=10.设 DE=x,则BH=x,AB=10-x,AD=10+x,
四边形ABCD的周长为AD+DC+BC+AB=10+x+4+4+10--x=28.故四边形 ABCD 的周长为28.
23|、(1)B (2)C
考试时间:120分钟 满分:120分
一、选择题
1.如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC=( )
A.27° B.30° C.54° D.55°
2.下列各组条件中,不能使两个直角三角形全等的是 ( )
A.一条直角边和它的对角分别相等
B.斜边和一条直角边分别相等
C.斜边和一锐角分别相等
D.两个锐角分别相等
3.已知∠AOB=60°,以O为圆心,任意长为半径作弧,分别交OA、OB于点M、N,分别以点M、N为圆心,大于 MN的长度为半径作弧,两弧在∠AOB 内交于点 P,以OP 为边作∠POC=15°,则∠BOC的度数为( )
A.15° B.45° C.15°或30° D.15°或45°
4.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是 ( )
A.24 B.30 C.36 D.42
5.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
6.如图,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使DE=AD,连接EC,则∠ECA 的度数为( )
A.30° B.35° C.40° D.45°
7.如图,在△ABC中,AD是∠BAC的外角平分线,P是AD 上异于点A的任意一点,设PB=m,PC=n,AB=c,AC=b,则m+n与b+c的大小关系是 ( )
A. m+n>b+c B. m+n
8.如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(3,1)、(4,3),在下列选项的E点坐标中,不能使△ABE与△ABC全等的是( )
A.(4,-1) B.(-1,3)
C.(-1,-1) D.(1,3)
9.如图,把△ABC剪成三部分,边AB,BC,AC放在同一直线l上,点O都落在直线 MN 上,直线 MN∥l.在△ABC 中,若∠BOC=130°,则∠BAC的度数为 ( )
A.70° B.75° C80° D.85°
10. 如图, 在△ABC 中,∠C= 90°. AD 平分∠BAC交BC 于点D,DE⊥AB于点E.给出下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE :S△ACD=BD:AC.其中正确的个数为( )
A.5 B.4 C.3 D.2
二、填空题
11.如图所示,△ABC≌△DCB,AF⊥BC于点F,DE⊥BC于点 E,已知 BC=18cm,且△ABC的面积为108cm ,则DE= cm.
12.如图,在△ABC中,点F在边BC上,FD⊥AC于点D,DE⊥AB 于点E,AD=CF,AE=CD,若∠CFD=40°,则∠EDF= .
13.如图,已知等边△ABC中,BD=CE,AD与BE 相交于点P,则∠APE的度数是 度.
14.如图,在△ABC中,AD 是∠BAC的平分线,AB=6cm,AC=8cm,则BD:CD= .
15.豫豫用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的长度为 cm.
三、解答题
16.(8分)如图,点C在线段BD 上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
17.(9分)如图,在四边形 ABCD中,AB=AD,在BC上求作一点 P 使△ABP≌△ADP.
(要求:用尺规作图,不写作法,保留作图痕迹)
18.(9分)如图, ,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 长为半作圆弧,两条圆弧交于点 P,作射线 AP交CD 于点M.
(1)若 求 的度数;
(2)若 垂足为 N,求证: ≌
19.(9分)如图, ,E是AB上的一点,且. 求证:
20.(9分)如图,C,E分别为 的边BD,AB上的点,且 ,求∠B的度数.
21.(10分)如图,已知 的角平分线BM,CN 相交于点 P.
(1)AP是否平分 请说明理由.
(2)由此题你得到的结论是 .
22.(10 分)如图,在四边形ABCD 中, ,AC平分 ,过点 C作CE⊥AD,垂足为 E, ,求四边形ABCD的周长.
23.(11分)课外兴趣小组活动时,老师提出了如下问题:
如图(1), 中,若 ,求BC边上的中线AD 的取值范围.经过组内合作交流,小明得到了如下的解决方法:延长AD 到点E,使 请根据小明的方法思考:
(1)由已知和作图能得到 ≌ 的理由是 .
A. SSS B. SAS C. AAS D. HL
(2)求得AD的取值范围是 .
第十二章综合测试卷
选择题
1、C 2、D 3、D 4、C 5、C 6、C 7、A 8、D 9、C 10、C
二、填空题
11、12 12、50°13、60 14、3:4 15、45
三、解答题
16、证明:∵AB⊥BD,DE⊥BD, AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠E=90°,
∴∠ACB=∠E.在△ABC和△CDE 中, (ASA),
∴AB=CD.
17、解:点P 如图所示.
18、(1) 解: ∵ AB∥CD,
∴∠ACD +∠CAB=180°.
又∵∠ACD=114°,
∴∠CAB = 66°.
由 作法 知, AM 是∠CAB 的平分线,
∠CAB=33°.
证明:由作法可知,AN 平分∠CAB,
∴∠CAM=∠MAB.
∵AB∥CD,
∴∠MAB=∠CMA,
∴∠CAM=∠CMA.
又∵CN⊥AM,CN= CN.
∴∠CNA =∠CNM= 90°,
∴△CAN≌△CMN(AAS).
证明:过点E 作EF⊥CD 于点 F,则∠EFC=∠EFD=90°.
又∵∠1=∠2,EF=EF,
∴△EFD≌△EFC(AAS),
∴DE =CE.
∵∠A=∠B =90°,
∴ 在 Rt△ADE 和 Rt△BEC 中,
△BEC(HL).
20、解:如图,连接 AC. 在△AEC 和△ADC 中,
∴∠AEC=∠D=70°,
∴∠BEC=180°-70°=110°,
∵∠ECD=150°,
∴∠B=∠ECD-∠BEC=150°-110°=40°.
21、解:(1)AP 平分∠BAC.理由如下:如图,过点 P 作PQ⊥BC 于点Q ,
PK⊥AB 于点 K,PL⊥AC 于点 L,
∵△ABC 的角平分线BM,CN 相交于点P,
∴PK=PQ,PL=PQ,∴PK=PL,∴AP 平分∠BAC.
(2)三角形的三条角平分线相交于一点 .
22、解:如图,过 C点作CH⊥AB,交 AB 的延长线于点 H.
∵AC 平分∠BAD,CH⊥AH,CE⊥AD.
∴CH=CE.
∵∠BAD+∠BCD=180°,
∴∠ABC+∠D =180°.
∵∠ABC+∠HBC =180°,
∴∠HBC=∠D.
又∵∠H=∠CED=90°.
∴△HBC≌△EDC(AAS).
∴HB=DE,BC=CD=4. 在 Rt△ACH 和 Rt△ACE 中,AC=ACC,
∴Rt△ACH≌Rt△ACE(HL).
∴AH=AE=10.设 DE=x,则BH=x,AB=10-x,AD=10+x,
四边形ABCD的周长为AD+DC+BC+AB=10+x+4+4+10--x=28.故四边形 ABCD 的周长为28.
23|、(1)B (2)C
