2024-2025学年内蒙古包头市高新区八年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年内蒙古包头市高新区八年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 18:12:41 | ||
图片预览



文档简介
2024-2025学年内蒙古包头市高新区八年级(上)期中数学试卷
一、选择题(每题3分,共30分)
1.(3分)9的平方根是( )
A.±3 B.3 C. D.
2.(3分)下列计算结果正确的是( )
A. B.
C. D.
3.(3分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.2,3,4 B.6,7,8 C.9,40,45 D.
4.(3分)已知点P的坐标为(﹣6,5),则点P关于y轴的对称点的坐标是( )
A.(﹣6,﹣5) B.(6,5) C.(6,﹣5) D.(5,﹣6)
5.(3分)已知(3,y1)和(﹣1,y2)是直线y=﹣3x上的两点,则y1和y2的大小关系是( )
A.y1<y2 B.y1>y2
C.y1=y2 D.以上都有可能
6.(3分)若是关于x、y的方程x+ay=3的一个解,则a的值为( )
A.1 B.﹣1 C.3 D.﹣3
7.(3分)若x,y为实数,且,则点P(x,y)到y轴的距离为( )
A.﹣5 B.2 C.5 D.﹣2
8.(3分)如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形E的面积是81,则图中所有正方形的面积和是( )
A.81 B.162 C.243 D.324
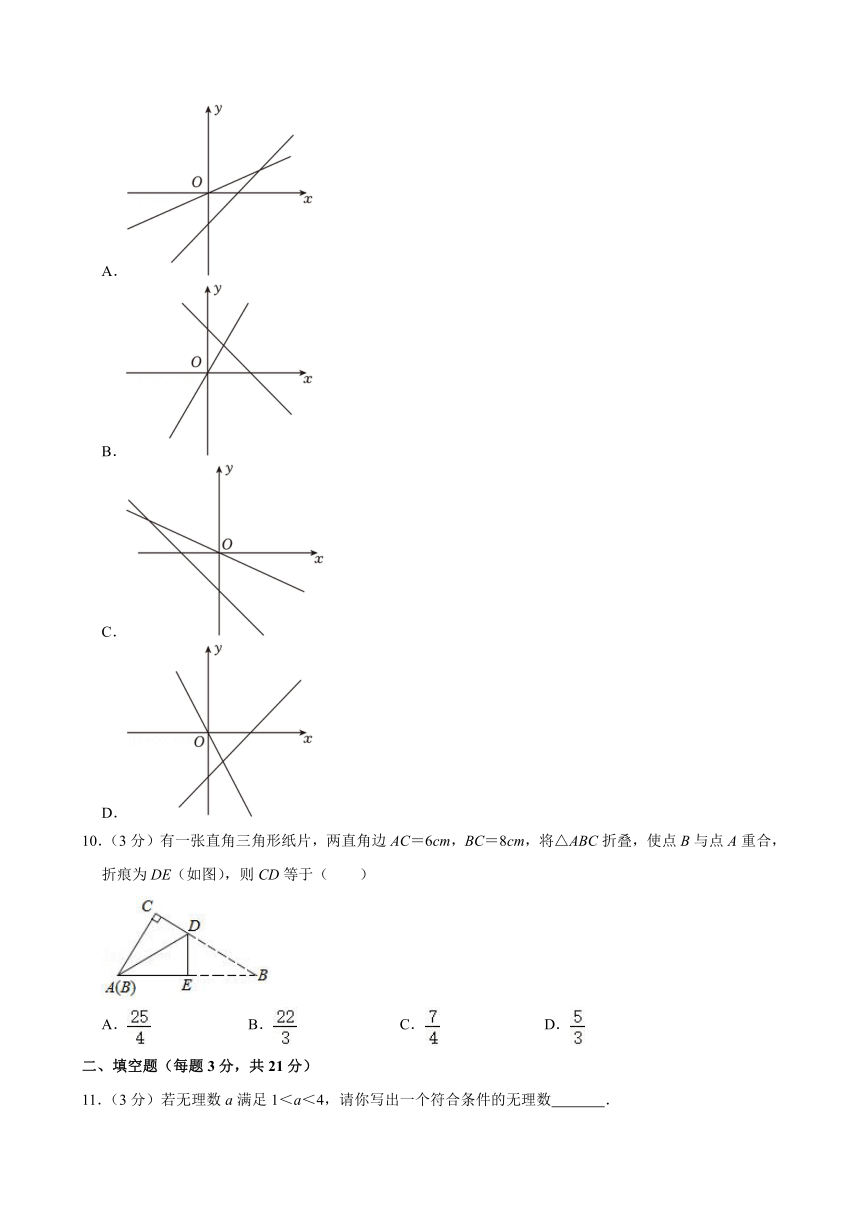
9.(3分)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
10.(3分)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )
A. B. C. D.
二、填空题(每题3分,共21分)
11.(3分)若无理数a满足1<a<4,请你写出一个符合条件的无理数 .
12.(3分)正比例函数y=kx的图象如图所示,则k的值为 .
13.(3分)已知点A(a+3,3a﹣6)在x轴上,则点A的坐标是 .
14.(3分)比较大小: 2; 3.85; .
15.(3分)如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 m.
16.(3分)在解关于x,y的方程组时,可以用①×2+②消去未知数x,也可以用①+②×5消去未知数y,则m﹣n= .
17.(3分)如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴于点C,则OC= .
三、解答题(共49分)
18.(6分)计算:
(1);
(2).
19.(6分)解方程组:
(1);
(2).
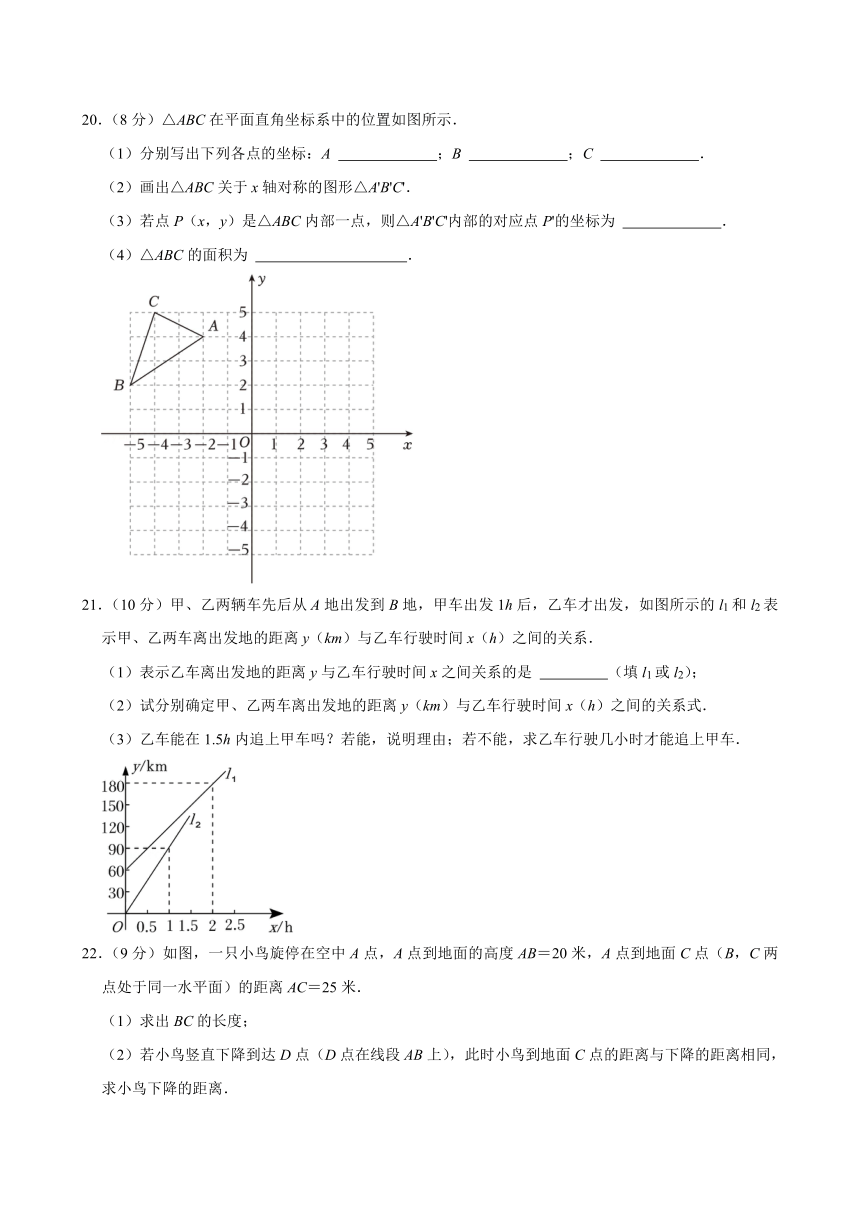
20.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ;B ;C .
(2)画出△ABC关于x轴对称的图形△A'B'C'.
(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 .
(4)△ABC的面积为 .
21.(10分)甲、乙两辆车先后从A地出发到B地,甲车出发1h后,乙车才出发,如图所示的l1和l2表示甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系.
(1)表示乙车离出发地的距离y与乙车行驶时间x之间关系的是 (填l1或l2);
(2)试分别确定甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系式.
(3)乙车能在1.5h内追上甲车吗?若能,说明理由;若不能,求乙车行驶几小时才能追上甲车.
22.(9分)如图,一只小鸟旋停在空中A点,A点到地面的高度AB=20米,A点到地面C点(B,C两点处于同一水平面)的距离AC=25米.
(1)求出BC的长度;
(2)若小鸟竖直下降到达D点(D点在线段AB上),此时小鸟到地面C点的距离与下降的距离相同,求小鸟下降的距离.
23.(10分)如图所示,在平面直角坐标系中,直线y=x+6与x轴交于点A,与y轴交于点B.过点B作BC⊥AB于点B,交x轴于点C.
(1)求点A和点B的坐标;
(2)求直线BC的函数表达式;
(3)在直线AB上是否存在点P,使△ACP的面积是△ABC面积的2倍?若存在,出点P的坐标;若不存在,请说明理由.
2024-2025学年内蒙古包头市高新区八年级(上)期中数学试卷
参考答案
一、选择题(每题3分,共30分)
1.(3分)9的平方根是( )
A.±3 B.3 C. D.
选:A.
2.(3分)下列计算结果正确的是( )
A. B.
C. D.
选:B.
3.(3分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.2,3,4 B.6,7,8 C.9,40,45 D.
选:D.
4.(3分)已知点P的坐标为(﹣6,5),则点P关于y轴的对称点的坐标是( )
A.(﹣6,﹣5) B.(6,5) C.(6,﹣5) D.(5,﹣6)
选:B.
5.(3分)已知(3,y1)和(﹣1,y2)是直线y=﹣3x上的两点,则y1和y2的大小关系是( )
A.y1<y2 B.y1>y2
C.y1=y2 D.以上都有可能
选:A.
6.(3分)若是关于x、y的方程x+ay=3的一个解,则a的值为( )
A.1 B.﹣1 C.3 D.﹣3
选:A.
7.(3分)若x,y为实数,且,则点P(x,y)到y轴的距离为( )
A.﹣5 B.2 C.5 D.﹣2
选:C.
8.(3分)如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形E的面积是81,则图中所有正方形的面积和是( )
A.81 B.162 C.243 D.324
选:C.
9.(3分)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
选:D.
10.(3分)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )
A. B. C. D.
选:C.
二、填空题(每题3分,共21分)
11.(3分)若无理数a满足1<a<4,请你写出一个符合条件的无理数 π .
12.(3分)正比例函数y=kx的图象如图所示,则k的值为 .
13.(3分)已知点A(a+3,3a﹣6)在x轴上,则点A的坐标是 (5,0) .
14.(3分)比较大小: < 2; > 3.85; < .
15.(3分)如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 3 m.
16.(3分)在解关于x,y的方程组时,可以用①×2+②消去未知数x,也可以用①+②×5消去未知数y,则m﹣n= .
17.(3分)如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴于点C,则OC= 2﹣2 .
三、解答题(共49分)
18.(6分)计算:
(1);
(2).
【解答】解:(1)原式=+6﹣4
=3;
(2)原式=()2﹣()2﹣(1﹣2+2)
=2﹣3﹣1+2﹣2
=﹣4+2.
19.(6分)解方程组:
(1);
(2).
【解答】解:(1),
①+②,得3x=9,
解得x=3,
把x=3代入②,得y=﹣2,
所以方程组的解是;
(2),
方程组可化为,
②×3,得9x﹣3y=﹣3③,
③﹣①,得5x=﹣15,
解得x=﹣3,
把x=﹣3代入②,得y=﹣8,
所以原方程组的解是.
20.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A (﹣2,4) ;B (﹣5,2) ;C (﹣4,5) .
(2)画出△ABC关于x轴对称的图形△A'B'C'.
(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 (x,﹣y) .
(4)△ABC的面积为 .
【解答】解:(1)由图可得,A(﹣2,4),B(﹣5,2),C(﹣4,5).
故答案为:(﹣2,4);(﹣5,2);(﹣4,5).
(2)如图,△A'B'C'即为所求.
(3)由题意得,△A'B'C'内部的对应点P'的坐标为(x,﹣y).
故答案为:(x,﹣y).
(4)△ABC的面积为==.
故答案为:.
21.(10分)甲、乙两辆车先后从A地出发到B地,甲车出发1h后,乙车才出发,如图所示的l1和l2表示甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系.
(1)表示乙车离出发地的距离y与乙车行驶时间x之间关系的是 l2 (填l1或l2);
(2)试分别确定甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系式.
(3)乙车能在1.5h内追上甲车吗?若能,说明理由;若不能,求乙车行驶几小时才能追上甲车.
【解答】解:(1)由函数图象得:
l2表示乙车离出发地的距离y与追赶时间x之间的关系;
故答案为:l2;
(2)甲车的速度为=60(km/h),乙车的速度为=90(km/h);
甲车的函数的关系式为:y1=60x+60;
乙车的函数关系式为:y2=90x;
(2)设乙车行驶a小时可以追上甲车,由题意得:
90a=60+60a,
解得:a=2.
∵1.5<2,
∴乙车不能在1.5小时内追上甲车.
乙车追上甲车时,乙车行驶了2小时.
22.(9分)如图,一只小鸟旋停在空中A点,A点到地面的高度AB=20米,A点到地面C点(B,C两点处于同一水平面)的距离AC=25米.
(1)求出BC的长度;
(2)若小鸟竖直下降到达D点(D点在线段AB上),此时小鸟到地面C点的距离与下降的距离相同,求小鸟下降的距离.
【解答】解:(1)由题意知∠B=90°,
∵AB=20米,AC=25米.
∴BC==15米,
(2)设AD=x,则CD=x,BD=20﹣x,
在Rt△BDC中,DC2=BD2+BC2,
∴x2=(20﹣x)2+152,
解得x=,
∴小鸟下降的距离为米.
23.(10分)如图所示,在平面直角坐标系中,直线y=x+6与x轴交于点A,与y轴交于点B.过点B作BC⊥AB于点B,交x轴于点C.
(1)求点A和点B的坐标;
(2)求直线BC的函数表达式;
(3)在直线AB上是否存在点P,使△ACP的面积是△ABC面积的2倍?若存在,出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵直线y=x+6与x轴交于点A,与y轴交于点B.
∴A(﹣6,0),B(0,6);
(2)∵BC⊥AB于点B,
∴kBC=﹣1,
∵B(0,6),
∴直线BC的解析式为:y=﹣x+6;
(3)由直线BC解析式y=﹣x+6,可得C(6,0),
S△ABC==36,
设点P的坐标为(m,m+6)
∵S△PAC=2S△ABC=72,
∴,
解得m=6或m=﹣18,
∴P(6,12)或(﹣18,﹣12).
一、选择题(每题3分,共30分)
1.(3分)9的平方根是( )
A.±3 B.3 C. D.
2.(3分)下列计算结果正确的是( )
A. B.
C. D.
3.(3分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.2,3,4 B.6,7,8 C.9,40,45 D.
4.(3分)已知点P的坐标为(﹣6,5),则点P关于y轴的对称点的坐标是( )
A.(﹣6,﹣5) B.(6,5) C.(6,﹣5) D.(5,﹣6)
5.(3分)已知(3,y1)和(﹣1,y2)是直线y=﹣3x上的两点,则y1和y2的大小关系是( )
A.y1<y2 B.y1>y2
C.y1=y2 D.以上都有可能
6.(3分)若是关于x、y的方程x+ay=3的一个解,则a的值为( )
A.1 B.﹣1 C.3 D.﹣3
7.(3分)若x,y为实数,且,则点P(x,y)到y轴的距离为( )
A.﹣5 B.2 C.5 D.﹣2
8.(3分)如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形E的面积是81,则图中所有正方形的面积和是( )
A.81 B.162 C.243 D.324
9.(3分)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
10.(3分)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )
A. B. C. D.
二、填空题(每题3分,共21分)
11.(3分)若无理数a满足1<a<4,请你写出一个符合条件的无理数 .
12.(3分)正比例函数y=kx的图象如图所示,则k的值为 .
13.(3分)已知点A(a+3,3a﹣6)在x轴上,则点A的坐标是 .
14.(3分)比较大小: 2; 3.85; .
15.(3分)如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 m.
16.(3分)在解关于x,y的方程组时,可以用①×2+②消去未知数x,也可以用①+②×5消去未知数y,则m﹣n= .
17.(3分)如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴于点C,则OC= .
三、解答题(共49分)
18.(6分)计算:
(1);
(2).
19.(6分)解方程组:
(1);
(2).
20.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ;B ;C .
(2)画出△ABC关于x轴对称的图形△A'B'C'.
(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 .
(4)△ABC的面积为 .
21.(10分)甲、乙两辆车先后从A地出发到B地,甲车出发1h后,乙车才出发,如图所示的l1和l2表示甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系.
(1)表示乙车离出发地的距离y与乙车行驶时间x之间关系的是 (填l1或l2);
(2)试分别确定甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系式.
(3)乙车能在1.5h内追上甲车吗?若能,说明理由;若不能,求乙车行驶几小时才能追上甲车.
22.(9分)如图,一只小鸟旋停在空中A点,A点到地面的高度AB=20米,A点到地面C点(B,C两点处于同一水平面)的距离AC=25米.
(1)求出BC的长度;
(2)若小鸟竖直下降到达D点(D点在线段AB上),此时小鸟到地面C点的距离与下降的距离相同,求小鸟下降的距离.
23.(10分)如图所示,在平面直角坐标系中,直线y=x+6与x轴交于点A,与y轴交于点B.过点B作BC⊥AB于点B,交x轴于点C.
(1)求点A和点B的坐标;
(2)求直线BC的函数表达式;
(3)在直线AB上是否存在点P,使△ACP的面积是△ABC面积的2倍?若存在,出点P的坐标;若不存在,请说明理由.
2024-2025学年内蒙古包头市高新区八年级(上)期中数学试卷
参考答案
一、选择题(每题3分,共30分)
1.(3分)9的平方根是( )
A.±3 B.3 C. D.
选:A.
2.(3分)下列计算结果正确的是( )
A. B.
C. D.
选:B.
3.(3分)下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.2,3,4 B.6,7,8 C.9,40,45 D.
选:D.
4.(3分)已知点P的坐标为(﹣6,5),则点P关于y轴的对称点的坐标是( )
A.(﹣6,﹣5) B.(6,5) C.(6,﹣5) D.(5,﹣6)
选:B.
5.(3分)已知(3,y1)和(﹣1,y2)是直线y=﹣3x上的两点,则y1和y2的大小关系是( )
A.y1<y2 B.y1>y2
C.y1=y2 D.以上都有可能
选:A.
6.(3分)若是关于x、y的方程x+ay=3的一个解,则a的值为( )
A.1 B.﹣1 C.3 D.﹣3
选:A.
7.(3分)若x,y为实数,且,则点P(x,y)到y轴的距离为( )
A.﹣5 B.2 C.5 D.﹣2
选:C.
8.(3分)如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形E的面积是81,则图中所有正方形的面积和是( )
A.81 B.162 C.243 D.324
选:C.
9.(3分)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
选:D.
10.(3分)有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )
A. B. C. D.
选:C.
二、填空题(每题3分,共21分)
11.(3分)若无理数a满足1<a<4,请你写出一个符合条件的无理数 π .
12.(3分)正比例函数y=kx的图象如图所示,则k的值为 .
13.(3分)已知点A(a+3,3a﹣6)在x轴上,则点A的坐标是 (5,0) .
14.(3分)比较大小: < 2; > 3.85; < .
15.(3分)如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是 3 m.
16.(3分)在解关于x,y的方程组时,可以用①×2+②消去未知数x,也可以用①+②×5消去未知数y,则m﹣n= .
17.(3分)如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴于点C,则OC= 2﹣2 .
三、解答题(共49分)
18.(6分)计算:
(1);
(2).
【解答】解:(1)原式=+6﹣4
=3;
(2)原式=()2﹣()2﹣(1﹣2+2)
=2﹣3﹣1+2﹣2
=﹣4+2.
19.(6分)解方程组:
(1);
(2).
【解答】解:(1),
①+②,得3x=9,
解得x=3,
把x=3代入②,得y=﹣2,
所以方程组的解是;
(2),
方程组可化为,
②×3,得9x﹣3y=﹣3③,
③﹣①,得5x=﹣15,
解得x=﹣3,
把x=﹣3代入②,得y=﹣8,
所以原方程组的解是.
20.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A (﹣2,4) ;B (﹣5,2) ;C (﹣4,5) .
(2)画出△ABC关于x轴对称的图形△A'B'C'.
(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 (x,﹣y) .
(4)△ABC的面积为 .
【解答】解:(1)由图可得,A(﹣2,4),B(﹣5,2),C(﹣4,5).
故答案为:(﹣2,4);(﹣5,2);(﹣4,5).
(2)如图,△A'B'C'即为所求.
(3)由题意得,△A'B'C'内部的对应点P'的坐标为(x,﹣y).
故答案为:(x,﹣y).
(4)△ABC的面积为==.
故答案为:.
21.(10分)甲、乙两辆车先后从A地出发到B地,甲车出发1h后,乙车才出发,如图所示的l1和l2表示甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系.
(1)表示乙车离出发地的距离y与乙车行驶时间x之间关系的是 l2 (填l1或l2);
(2)试分别确定甲、乙两车离出发地的距离y(km)与乙车行驶时间x(h)之间的关系式.
(3)乙车能在1.5h内追上甲车吗?若能,说明理由;若不能,求乙车行驶几小时才能追上甲车.
【解答】解:(1)由函数图象得:
l2表示乙车离出发地的距离y与追赶时间x之间的关系;
故答案为:l2;
(2)甲车的速度为=60(km/h),乙车的速度为=90(km/h);
甲车的函数的关系式为:y1=60x+60;
乙车的函数关系式为:y2=90x;
(2)设乙车行驶a小时可以追上甲车,由题意得:
90a=60+60a,
解得:a=2.
∵1.5<2,
∴乙车不能在1.5小时内追上甲车.
乙车追上甲车时,乙车行驶了2小时.
22.(9分)如图,一只小鸟旋停在空中A点,A点到地面的高度AB=20米,A点到地面C点(B,C两点处于同一水平面)的距离AC=25米.
(1)求出BC的长度;
(2)若小鸟竖直下降到达D点(D点在线段AB上),此时小鸟到地面C点的距离与下降的距离相同,求小鸟下降的距离.
【解答】解:(1)由题意知∠B=90°,
∵AB=20米,AC=25米.
∴BC==15米,
(2)设AD=x,则CD=x,BD=20﹣x,
在Rt△BDC中,DC2=BD2+BC2,
∴x2=(20﹣x)2+152,
解得x=,
∴小鸟下降的距离为米.
23.(10分)如图所示,在平面直角坐标系中,直线y=x+6与x轴交于点A,与y轴交于点B.过点B作BC⊥AB于点B,交x轴于点C.
(1)求点A和点B的坐标;
(2)求直线BC的函数表达式;
(3)在直线AB上是否存在点P,使△ACP的面积是△ABC面积的2倍?若存在,出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵直线y=x+6与x轴交于点A,与y轴交于点B.
∴A(﹣6,0),B(0,6);
(2)∵BC⊥AB于点B,
∴kBC=﹣1,
∵B(0,6),
∴直线BC的解析式为:y=﹣x+6;
(3)由直线BC解析式y=﹣x+6,可得C(6,0),
S△ABC==36,
设点P的坐标为(m,m+6)
∵S△PAC=2S△ABC=72,
∴,
解得m=6或m=﹣18,
∴P(6,12)或(﹣18,﹣12).
同课章节目录
