2024-2025学年浙江省杭州市天杭教育集团思远学部九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年浙江省杭州市天杭教育集团思远学部九年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 18:15:55 | ||
图片预览


文档简介
2024-2025学年浙江省杭州市天杭教育集团思远学部九年级(上)期中数学试卷
一、选择题(本大题有10个小题,每小题3分,共30分)
1.(3分)下列事件是必然事件的是( )
A.圆内接四边形对角和是180°
B.九年级开展篮球赛,901班获得冠军
C.抛掷一枚硬币,正面朝上
D.打开电视,正好播放神舟十七号载人飞船发射实况
2.(3分)已知点P是线段AB的黄金分割点(AP>BP),若AB=2,则AP为( )
A. B. C. D.
3.(3分)如图,△ABC内接于⊙O,CD是⊙O的直径,连接BD,∠DCA=39°,则∠ABC的度数是( )
A.39° B.45° C.49° D.51°
4.(3分)由二次函数y=2x2图象平移得到二次函数y=2(x﹣m)2+n(m>0,n>0)图象,下列哪种平移方式可以实现( )
A.向右平移m个单位,再向上平移n个单位
B.向右平移m个单位,再向下平移n个单位
C.向左平移m个单位,再向上平移n个单位
D.向左平移m个单位,再向下平移n个单位
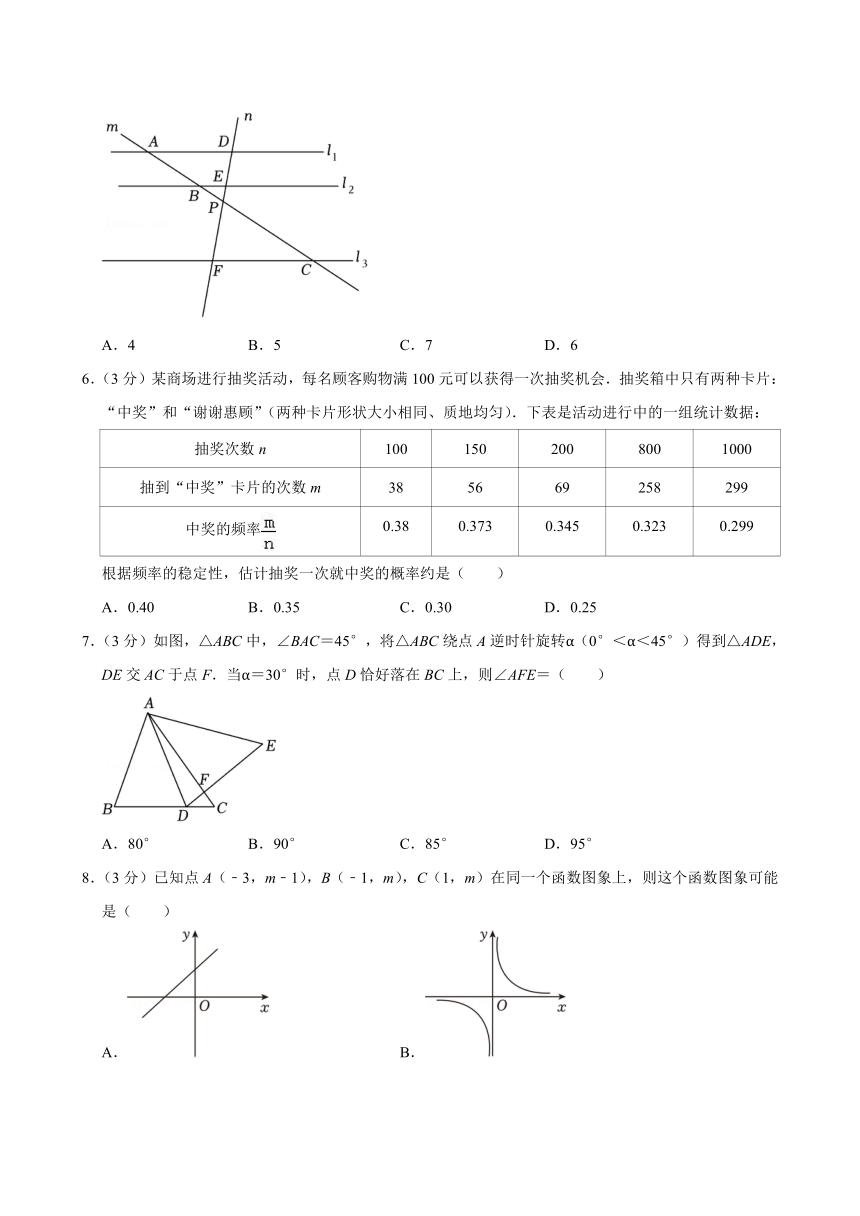
5.(3分)如图,已知直线l1∥l2∥l3,直线m和直线n分别交l1、l2、l3于点A,B,C,D,E,F,直线m和直线n交于点P.若DE=2,EF=4,AB=4,若BP:CP=1:3,则CP=( )
A.4 B.5 C.7 D.6
6.(3分)某商场进行抽奖活动,每名顾客购物满100元可以获得一次抽奖机会.抽奖箱中只有两种卡片:“中奖”和“谢谢惠顾”(两种卡片形状大小相同、质地均匀).下表是活动进行中的一组统计数据:
抽奖次数n 100 150 200 800 1000
抽到“中奖”卡片的次数m 38 56 69 258 299
中奖的频率 0.38 0.373 0.345 0.323 0.299
根据频率的稳定性,估计抽奖一次就中奖的概率约是( )
A.0.40 B.0.35 C.0.30 D.0.25
7.(3分)如图,△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转α(0°<α<45°)得到△ADE,DE交AC于点F.当α=30°时,点D恰好落在BC上,则∠AFE=( )
A.80° B.90° C.85° D.95°
8.(3分)已知点A(﹣3,m﹣1),B(﹣1,m),C(1,m)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
9.(3分)如图,AB是⊙O的直径,弦CD垂直平分OB,点E在上,连接CE,AE.若CE平分∠OCD,则∠A:∠E=( )
A.2:3 B.3:4 C.4:5 D.5:6
10.(3分)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
二、填空题(本大题有6个小题,每小题3分,共18分)
11.(3分)已知a:b=2:3,那么的值是 .
12.(3分)有10张卡片,每张卡片上分别写有不同的从1到10的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 .
13.(3分)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 .(只需写出一个条件即可)
14.(3分)已知二次函数y=ax2﹣4ax+4a+1(a≠0),则此函数的顶点坐标是 ;若a<0,当1≤x≤4时,函数有最小值a﹣1,则a= .
15.(3分)图1为一圆形纸片,A、B、C为圆周上三点,其中AC为直径,以AB为折线将纸片向右折叠,纸片盖住部分的AC,且交AC于点D,如图2所示,若弧BC为37°,则的度数= .
16.(3分)如图,在矩形ABCD中,AD=5,AB=3,点E在AB上,,在矩形内找一点P.使得∠BPE=60°,则BE= ,线段PD的最小值为 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤。
17.二次函数y=a(x+1)2+4的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0).
(1)求点B的坐标和a的值;
(2)当y>0时,直接写出x的取值范围.
18.已知:如图△ABC内接于圆O,AB=AC,D为弧BC上任意一点,连接AD,BD.
(1)若∠ADB=65°,求∠BAC的度数;
(2)求证:∠ABD=∠AEB.
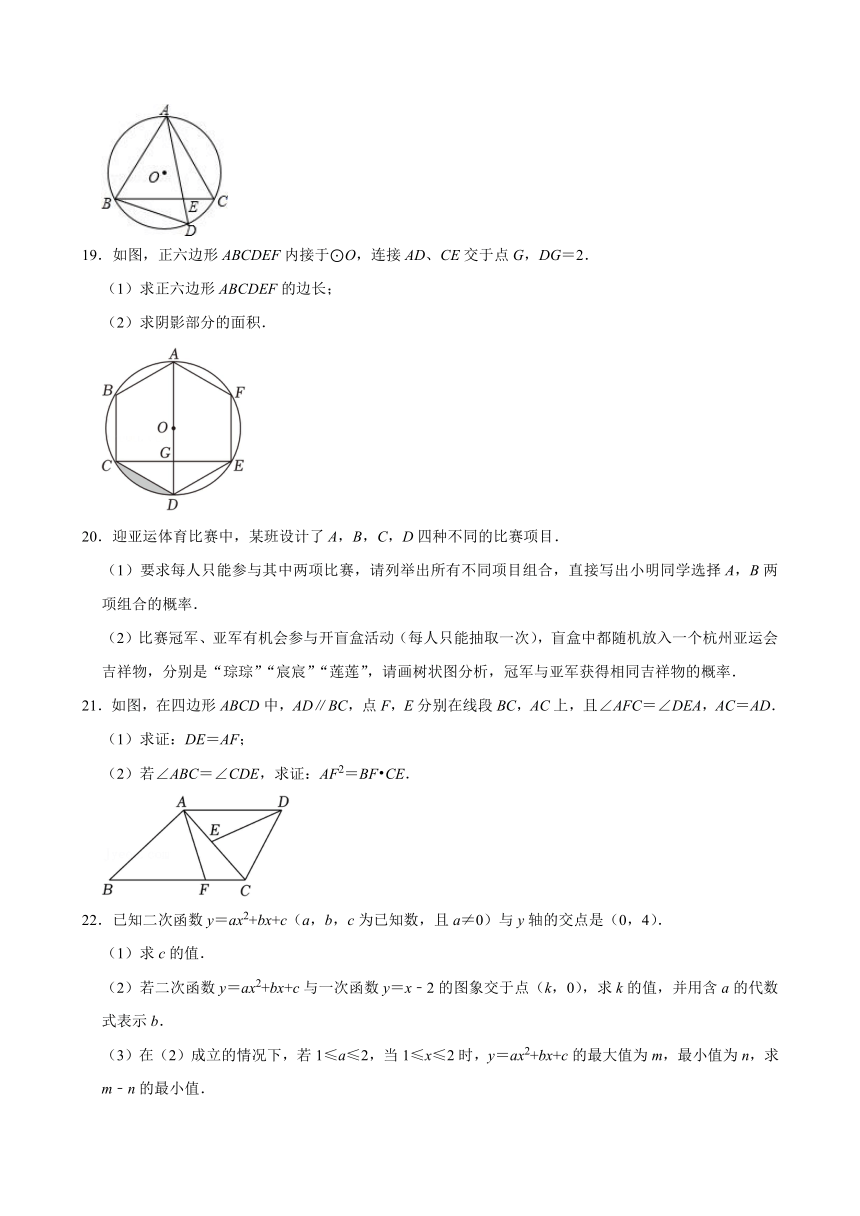
19.如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
20.迎亚运体育比赛中,某班设计了A,B,C,D四种不同的比赛项目.
(1)要求每人只能参与其中两项比赛,请列举出所有不同项目组合,直接写出小明同学选择A,B两项组合的概率.
(2)比赛冠军、亚军有机会参与开盲盒活动(每人只能抽取一次),盲盒中都随机放入一个杭州亚运会吉祥物,分别是“琮琮”“宸宸”“莲莲”,请画树状图分析,冠军与亚军获得相同吉祥物的概率.
21.如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
22.已知二次函数y=ax2+bx+c(a,b,c为已知数,且a≠0)与y轴的交点是(0,4).
(1)求c的值.
(2)若二次函数y=ax2+bx+c与一次函数y=x﹣2的图象交于点(k,0),求k的值,并用含a的代数式表示b.
(3)在(2)成立的情况下,若1≤a≤2,当1≤x≤2时,y=ax2+bx+c的最大值为m,最小值为n,求m﹣n的最小值.
23.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.
素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1 确定桥拱形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2 探究悬挂范围 在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3 拟定设计方案 给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
24.如图1,已知AB为⊙O的直径,弦CD⊥AB于点E,G是上一点,连结AD,AG,DG.
(1)求证:∠AGD=∠ADC;
(2)如图2,延长AG,DC相交于点F,连结CG.
①已知AG=6,GF=4,求AD的长;
②记DG与AB的交点为P,若AB=10,CD=8,当AG=AP时,求的值.
2024-2025学年浙江省杭州市天杭教育集团思远学部九年级(上)期中数学试卷
参考答案
一、选择题(本大题有10个小题,每小题3分,共30分)
1.(3分)下列事件是必然事件的是( )
A.圆内接四边形对角和是180°
B.九年级开展篮球赛,901班获得冠军
C.抛掷一枚硬币,正面朝上
D.打开电视,正好播放神舟十七号载人飞船发射实况
选:A.
2.(3分)已知点P是线段AB的黄金分割点(AP>BP),若AB=2,则AP为( )
A. B. C. D.
选:B.
3.(3分)如图,△ABC内接于⊙O,CD是⊙O的直径,连接BD,∠DCA=39°,则∠ABC的度数是( )
A.39° B.45° C.49° D.51°
选:D.
4.(3分)由二次函数y=2x2图象平移得到二次函数y=2(x﹣m)2+n(m>0,n>0)图象,下列哪种平移方式可以实现( )
A.向右平移m个单位,再向上平移n个单位
B.向右平移m个单位,再向下平移n个单位
C.向左平移m个单位,再向上平移n个单位
D.向左平移m个单位,再向下平移n个单位
选:A.
5.(3分)如图,已知直线l1∥l2∥l3,直线m和直线n分别交l1、l2、l3于点A,B,C,D,E,F,直线m和直线n交于点P.若DE=2,EF=4,AB=4,若BP:CP=1:3,则CP=( )
A.4 B.5 C.7 D.6
选:D.
6.(3分)某商场进行抽奖活动,每名顾客购物满100元可以获得一次抽奖机会.抽奖箱中只有两种卡片:“中奖”和“谢谢惠顾”(两种卡片形状大小相同、质地均匀).下表是活动进行中的一组统计数据:
抽奖次数n 100 150 200 800 1000
抽到“中奖”卡片的次数m 38 56 69 258 299
中奖的频率 0.38 0.373 0.345 0.323 0.299
根据频率的稳定性,估计抽奖一次就中奖的概率约是( )
A.0.40 B.0.35 C.0.30 D.0.25
选:C.
7.(3分)如图,△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转α(0°<α<45°)得到△ADE,DE交AC于点F.当α=30°时,点D恰好落在BC上,则∠AFE=( )
A.80° B.90° C.85° D.95°
选:B.
8.(3分)已知点A(﹣3,m﹣1),B(﹣1,m),C(1,m)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
选:C.
9.(3分)如图,AB是⊙O的直径,弦CD垂直平分OB,点E在上,连接CE,AE.若CE平分∠OCD,则∠A:∠E=( )
A.2:3 B.3:4 C.4:5 D.5:6
选:B.
10.(3分)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
选:B.
二、填空题(本大题有6个小题,每小题3分,共18分)
11.(3分)已知a:b=2:3,那么的值是 .
12.(3分)有10张卡片,每张卡片上分别写有不同的从1到10的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 .
13.(3分)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 ∠A=∠C(答案不唯一) .(只需写出一个条件即可)
14.(3分)已知二次函数y=ax2﹣4ax+4a+1(a≠0),则此函数的顶点坐标是 (2,1) ;若a<0,当1≤x≤4时,函数有最小值a﹣1,则a= ﹣ .
15.(3分)图1为一圆形纸片,A、B、C为圆周上三点,其中AC为直径,以AB为折线将纸片向右折叠,纸片盖住部分的AC,且交AC于点D,如图2所示,若弧BC为37°,则的度数= 106° .
16.(3分)如图,在矩形ABCD中,AD=5,AB=3,点E在AB上,,在矩形内找一点P.使得∠BPE=60°,则BE= 2 ,线段PD的最小值为 2﹣2 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤。
17.二次函数y=a(x+1)2+4的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0).
(1)求点B的坐标和a的值;
(2)当y>0时,直接写出x的取值范围.
【解答】解:(1)∵二次函数的对称轴为直线x=﹣1,A点坐标为(﹣3,0),
∴点B的坐标为(1,0),
把点B坐标代入y=a(x+1)2+4得,4a+4=0,
解得a=﹣1;
(2)∵a<0,二次函数y=a(x+1)2+4的图象与x轴交点为(﹣3,0)和(1,0),
∴当y>0时,x的取值范围为﹣3<x<1.
18.已知:如图△ABC内接于圆O,AB=AC,D为弧BC上任意一点,连接AD,BD.
(1)若∠ADB=65°,求∠BAC的度数;
(2)求证:∠ABD=∠AEB.
【解答】(1)解:∠ACB=∠ADB=65°,
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣65°﹣65°=50°;
(2)证明:∵∠AEB=∠EAC+∠ACB,
而∠ABC=∠ACB,∠EAC=∠DBC,
∴∠AEB=∠DBC+∠ABC,
即∠ABD=∠AEB.
19.如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
【解答】解:(1)如图,连接OC,则CG⊥OD,
∵正六边形ABCDEF内接于⊙O,
∴△COD是正三角形,
∴∠COD=60°,
∵CG⊥OD,
∴OG=DG=OD=2,
∴OC=2OG=4,
即正六边形的边长为4;
(2)在Rt△COD中,OG=2,∠COG=60°,
∴CG=OG=2,
∴S阴影部分=S扇形COD﹣S△COD
=﹣×4×2
=﹣4.
20.迎亚运体育比赛中,某班设计了A,B,C,D四种不同的比赛项目.
(1)要求每人只能参与其中两项比赛,请列举出所有不同项目组合,直接写出小明同学选择A,B两项组合的概率.
(2)比赛冠军、亚军有机会参与开盲盒活动(每人只能抽取一次),盲盒中都随机放入一个杭州亚运会吉祥物,分别是“琮琮”“宸宸”“莲莲”,请画树状图分析,冠军与亚军获得相同吉祥物的概率.
【解答】解:(1)列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
由表格可知,共有12种等可能的结果,其中小明同学选择A,B两项组合的结果有2种,
∴小明同学选择A,B两项组合的概率为=.
(2)将“琮琮”“宸宸”“莲莲”分别记为a,b,c,
画树状图如下:
共有9种等可能的结果,其中冠军与亚军获得相同吉祥物的结果有3种,
∴冠军与亚军获得相同吉祥物的概率为=.
21.如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
【解答】证明:(1)∵AD∥BC,
∴∠ACF=∠DAC
∵∠AFC=∠DEA,AC=AD,
∴△ACF≌△DAE(AAS),
∴AF=DE;
(2)∵△ACF≌△DAE,
∴∠AFC=∠DEA,
∴∠AFB=∠DEC,
∵∠ABC=∠CDE,
∴△ABF∽△CDE,
∴=,
∴AF DE=BF CE,
∵AF=DE,
∴AF2=BF CE.
22.已知二次函数y=ax2+bx+c(a,b,c为已知数,且a≠0)与y轴的交点是(0,4).
(1)求c的值.
(2)若二次函数y=ax2+bx+c与一次函数y=x﹣2的图象交于点(k,0),求k的值,并用含a的代数式表示b.
(3)在(2)成立的情况下,若1≤a≤2,当1≤x≤2时,y=ax2+bx+c的最大值为m,最小值为n,求m﹣n的最小值.
【解答】解:(1)把(0,4)代入y=ax2+bx+c,即c=4.
(2)由题意知点(k,0)过一次函数y=x﹣2,则k=2,
由(1)知二次函数为:y=ax2+bx+4,
∵(2,0)在二次函数y=ax2+bx+4上,
∴a×22+b×2+4=0,则b=﹣2a﹣2;
(3)由(2)知二次函数为:y=ax2﹣(2a+2)x+4,则函数对称轴为,
∵1≤a≤2,
∴,
∴,
∵1≤x≤2时,y=ax2﹣(2a+2)x+4的最大值为m,最小值为n,
∴m=a×12﹣(2a+2)×1+4=﹣a+2,,
则,
∵a=2,,
∴m﹣n的最小值为.
23.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.
素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1 确定桥拱形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2 探究悬挂范围 在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3 拟定设计方案 给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
【解答】解:任务1:
以拱顶为原点,建立如图1所示的直角坐标系,则顶点为(0,0),且过点B(10,﹣5),
设抛物线的解析式为:y=ax2,
把点B(10,﹣5)代入得:100a=﹣5,
∴a=﹣,
∴抛物线的函数表达式为:y=﹣x2;
任务2:
∵该河段水位再涨1.8m达到最高,灯笼底部距离水面不小于1m,灯笼长0.4m,
∴当悬挂点的纵坐标y≥﹣5+1.8+1+0.4=﹣1.8,
即悬挂点的纵坐标的最小值是﹣1.8m,
当y=﹣1.8时,﹣x2=﹣1.8,
∴x=±6,
∴悬挂点的横坐标的取值范围是:﹣6≤x≤6;
任务3:
方案一:如图2(坐标轴的横轴),从顶点处开始悬挂灯笼,
∵﹣6≤x≤6,相邻两盏灯笼悬挂点的水平间距均为1.6m,
∴若顶点一侧悬挂4盏灯笼时,1.6×4>6,
若顶点一侧悬挂3盏灯笼时,1.6×3<6,
∴顶点一侧最多悬挂3盏灯笼,
∵灯笼挂满后成轴对称分布,
∴共可挂7盏灯笼,
∴最左边一盏灯笼的横坐标为:﹣1.6×3=﹣4.8;
方案二:如图3,
∵若顶点一侧悬挂5盏灯笼时,0.8+1.6×(5﹣1)>6,
若顶点一侧悬挂4盏灯笼时,0.8+1.6×(4﹣1)<6,
∴顶点一侧最多悬挂4盏灯笼,
∵灯笼挂满后成轴对称分布,
∴共可挂8盏灯笼,
∴最左边一盏灯笼的横坐标为:﹣0.8﹣1.6×3=﹣5.6.
24.如图1,已知AB为⊙O的直径,弦CD⊥AB于点E,G是上一点,连结AD,AG,DG.
(1)求证:∠AGD=∠ADC;
(2)如图2,延长AG,DC相交于点F,连结CG.
①已知AG=6,GF=4,求AD的长;
②记DG与AB的交点为P,若AB=10,CD=8,当AG=AP时,求的值.
【解答】(1)证明:∵AB是⊙O直径,AB⊥CD,
∴=,
∴∠AGD=∠ADC;
(2)解:∵∠AGD=∠ADC,∠DAG=∠FAD,
∴△DAG∽△FAD,
∴,
∴AD2=AG×AF=6×(6+4)=60,
∴AD=2;
②连接OD.BD,BC,如图:
∵AB是⊙O直径,AB⊥CD,
∴DE=CE=CD=4.
∵OA=OB=OD=5,
∴OE=3.
∴BE=OB=OE=2,
∴BC===2,
∵AP=AG,
∴∠AGP=∠APG=∠DBA=∠DPB,
∴DP=DB,
∵AB⊥CD,
∴PE=BE=2,DC平分∠BDP,
∴AG=AP=AB﹣PE﹣BE=10﹣2﹣2=6,,
∴CG=BC=2,
∵四边形ADCG是圆的内接四边形,
∴∠CGF=∠ADC,∠GCF=∠DAG,
由(1)可知∠AGD=∠ADC,
∴∠CGF=∠AGD,
∴△CGF∽△AGD,
∴===.
一、选择题(本大题有10个小题,每小题3分,共30分)
1.(3分)下列事件是必然事件的是( )
A.圆内接四边形对角和是180°
B.九年级开展篮球赛,901班获得冠军
C.抛掷一枚硬币,正面朝上
D.打开电视,正好播放神舟十七号载人飞船发射实况
2.(3分)已知点P是线段AB的黄金分割点(AP>BP),若AB=2,则AP为( )
A. B. C. D.
3.(3分)如图,△ABC内接于⊙O,CD是⊙O的直径,连接BD,∠DCA=39°,则∠ABC的度数是( )
A.39° B.45° C.49° D.51°
4.(3分)由二次函数y=2x2图象平移得到二次函数y=2(x﹣m)2+n(m>0,n>0)图象,下列哪种平移方式可以实现( )
A.向右平移m个单位,再向上平移n个单位
B.向右平移m个单位,再向下平移n个单位
C.向左平移m个单位,再向上平移n个单位
D.向左平移m个单位,再向下平移n个单位
5.(3分)如图,已知直线l1∥l2∥l3,直线m和直线n分别交l1、l2、l3于点A,B,C,D,E,F,直线m和直线n交于点P.若DE=2,EF=4,AB=4,若BP:CP=1:3,则CP=( )
A.4 B.5 C.7 D.6
6.(3分)某商场进行抽奖活动,每名顾客购物满100元可以获得一次抽奖机会.抽奖箱中只有两种卡片:“中奖”和“谢谢惠顾”(两种卡片形状大小相同、质地均匀).下表是活动进行中的一组统计数据:
抽奖次数n 100 150 200 800 1000
抽到“中奖”卡片的次数m 38 56 69 258 299
中奖的频率 0.38 0.373 0.345 0.323 0.299
根据频率的稳定性,估计抽奖一次就中奖的概率约是( )
A.0.40 B.0.35 C.0.30 D.0.25
7.(3分)如图,△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转α(0°<α<45°)得到△ADE,DE交AC于点F.当α=30°时,点D恰好落在BC上,则∠AFE=( )
A.80° B.90° C.85° D.95°
8.(3分)已知点A(﹣3,m﹣1),B(﹣1,m),C(1,m)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
9.(3分)如图,AB是⊙O的直径,弦CD垂直平分OB,点E在上,连接CE,AE.若CE平分∠OCD,则∠A:∠E=( )
A.2:3 B.3:4 C.4:5 D.5:6
10.(3分)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
二、填空题(本大题有6个小题,每小题3分,共18分)
11.(3分)已知a:b=2:3,那么的值是 .
12.(3分)有10张卡片,每张卡片上分别写有不同的从1到10的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 .
13.(3分)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 .(只需写出一个条件即可)
14.(3分)已知二次函数y=ax2﹣4ax+4a+1(a≠0),则此函数的顶点坐标是 ;若a<0,当1≤x≤4时,函数有最小值a﹣1,则a= .
15.(3分)图1为一圆形纸片,A、B、C为圆周上三点,其中AC为直径,以AB为折线将纸片向右折叠,纸片盖住部分的AC,且交AC于点D,如图2所示,若弧BC为37°,则的度数= .
16.(3分)如图,在矩形ABCD中,AD=5,AB=3,点E在AB上,,在矩形内找一点P.使得∠BPE=60°,则BE= ,线段PD的最小值为 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤。
17.二次函数y=a(x+1)2+4的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0).
(1)求点B的坐标和a的值;
(2)当y>0时,直接写出x的取值范围.
18.已知:如图△ABC内接于圆O,AB=AC,D为弧BC上任意一点,连接AD,BD.
(1)若∠ADB=65°,求∠BAC的度数;
(2)求证:∠ABD=∠AEB.
19.如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
20.迎亚运体育比赛中,某班设计了A,B,C,D四种不同的比赛项目.
(1)要求每人只能参与其中两项比赛,请列举出所有不同项目组合,直接写出小明同学选择A,B两项组合的概率.
(2)比赛冠军、亚军有机会参与开盲盒活动(每人只能抽取一次),盲盒中都随机放入一个杭州亚运会吉祥物,分别是“琮琮”“宸宸”“莲莲”,请画树状图分析,冠军与亚军获得相同吉祥物的概率.
21.如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
22.已知二次函数y=ax2+bx+c(a,b,c为已知数,且a≠0)与y轴的交点是(0,4).
(1)求c的值.
(2)若二次函数y=ax2+bx+c与一次函数y=x﹣2的图象交于点(k,0),求k的值,并用含a的代数式表示b.
(3)在(2)成立的情况下,若1≤a≤2,当1≤x≤2时,y=ax2+bx+c的最大值为m,最小值为n,求m﹣n的最小值.
23.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.
素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1 确定桥拱形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2 探究悬挂范围 在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3 拟定设计方案 给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
24.如图1,已知AB为⊙O的直径,弦CD⊥AB于点E,G是上一点,连结AD,AG,DG.
(1)求证:∠AGD=∠ADC;
(2)如图2,延长AG,DC相交于点F,连结CG.
①已知AG=6,GF=4,求AD的长;
②记DG与AB的交点为P,若AB=10,CD=8,当AG=AP时,求的值.
2024-2025学年浙江省杭州市天杭教育集团思远学部九年级(上)期中数学试卷
参考答案
一、选择题(本大题有10个小题,每小题3分,共30分)
1.(3分)下列事件是必然事件的是( )
A.圆内接四边形对角和是180°
B.九年级开展篮球赛,901班获得冠军
C.抛掷一枚硬币,正面朝上
D.打开电视,正好播放神舟十七号载人飞船发射实况
选:A.
2.(3分)已知点P是线段AB的黄金分割点(AP>BP),若AB=2,则AP为( )
A. B. C. D.
选:B.
3.(3分)如图,△ABC内接于⊙O,CD是⊙O的直径,连接BD,∠DCA=39°,则∠ABC的度数是( )
A.39° B.45° C.49° D.51°
选:D.
4.(3分)由二次函数y=2x2图象平移得到二次函数y=2(x﹣m)2+n(m>0,n>0)图象,下列哪种平移方式可以实现( )
A.向右平移m个单位,再向上平移n个单位
B.向右平移m个单位,再向下平移n个单位
C.向左平移m个单位,再向上平移n个单位
D.向左平移m个单位,再向下平移n个单位
选:A.
5.(3分)如图,已知直线l1∥l2∥l3,直线m和直线n分别交l1、l2、l3于点A,B,C,D,E,F,直线m和直线n交于点P.若DE=2,EF=4,AB=4,若BP:CP=1:3,则CP=( )
A.4 B.5 C.7 D.6
选:D.
6.(3分)某商场进行抽奖活动,每名顾客购物满100元可以获得一次抽奖机会.抽奖箱中只有两种卡片:“中奖”和“谢谢惠顾”(两种卡片形状大小相同、质地均匀).下表是活动进行中的一组统计数据:
抽奖次数n 100 150 200 800 1000
抽到“中奖”卡片的次数m 38 56 69 258 299
中奖的频率 0.38 0.373 0.345 0.323 0.299
根据频率的稳定性,估计抽奖一次就中奖的概率约是( )
A.0.40 B.0.35 C.0.30 D.0.25
选:C.
7.(3分)如图,△ABC中,∠BAC=45°,将△ABC绕点A逆时针旋转α(0°<α<45°)得到△ADE,DE交AC于点F.当α=30°时,点D恰好落在BC上,则∠AFE=( )
A.80° B.90° C.85° D.95°
选:B.
8.(3分)已知点A(﹣3,m﹣1),B(﹣1,m),C(1,m)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
选:C.
9.(3分)如图,AB是⊙O的直径,弦CD垂直平分OB,点E在上,连接CE,AE.若CE平分∠OCD,则∠A:∠E=( )
A.2:3 B.3:4 C.4:5 D.5:6
选:B.
10.(3分)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
选:B.
二、填空题(本大题有6个小题,每小题3分,共18分)
11.(3分)已知a:b=2:3,那么的值是 .
12.(3分)有10张卡片,每张卡片上分别写有不同的从1到10的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是 .
13.(3分)如图,AC、BD交于点O,连接AB、CD,若要使△AOB∽△COD,可以添加条件 ∠A=∠C(答案不唯一) .(只需写出一个条件即可)
14.(3分)已知二次函数y=ax2﹣4ax+4a+1(a≠0),则此函数的顶点坐标是 (2,1) ;若a<0,当1≤x≤4时,函数有最小值a﹣1,则a= ﹣ .
15.(3分)图1为一圆形纸片,A、B、C为圆周上三点,其中AC为直径,以AB为折线将纸片向右折叠,纸片盖住部分的AC,且交AC于点D,如图2所示,若弧BC为37°,则的度数= 106° .
16.(3分)如图,在矩形ABCD中,AD=5,AB=3,点E在AB上,,在矩形内找一点P.使得∠BPE=60°,则BE= 2 ,线段PD的最小值为 2﹣2 .
三、解答题:本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤。
17.二次函数y=a(x+1)2+4的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0).
(1)求点B的坐标和a的值;
(2)当y>0时,直接写出x的取值范围.
【解答】解:(1)∵二次函数的对称轴为直线x=﹣1,A点坐标为(﹣3,0),
∴点B的坐标为(1,0),
把点B坐标代入y=a(x+1)2+4得,4a+4=0,
解得a=﹣1;
(2)∵a<0,二次函数y=a(x+1)2+4的图象与x轴交点为(﹣3,0)和(1,0),
∴当y>0时,x的取值范围为﹣3<x<1.
18.已知:如图△ABC内接于圆O,AB=AC,D为弧BC上任意一点,连接AD,BD.
(1)若∠ADB=65°,求∠BAC的度数;
(2)求证:∠ABD=∠AEB.
【解答】(1)解:∠ACB=∠ADB=65°,
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣65°﹣65°=50°;
(2)证明:∵∠AEB=∠EAC+∠ACB,
而∠ABC=∠ACB,∠EAC=∠DBC,
∴∠AEB=∠DBC+∠ABC,
即∠ABD=∠AEB.
19.如图,正六边形ABCDEF内接于⊙O,连接AD、CE交于点G,DG=2.
(1)求正六边形ABCDEF的边长;
(2)求阴影部分的面积.
【解答】解:(1)如图,连接OC,则CG⊥OD,
∵正六边形ABCDEF内接于⊙O,
∴△COD是正三角形,
∴∠COD=60°,
∵CG⊥OD,
∴OG=DG=OD=2,
∴OC=2OG=4,
即正六边形的边长为4;
(2)在Rt△COD中,OG=2,∠COG=60°,
∴CG=OG=2,
∴S阴影部分=S扇形COD﹣S△COD
=﹣×4×2
=﹣4.
20.迎亚运体育比赛中,某班设计了A,B,C,D四种不同的比赛项目.
(1)要求每人只能参与其中两项比赛,请列举出所有不同项目组合,直接写出小明同学选择A,B两项组合的概率.
(2)比赛冠军、亚军有机会参与开盲盒活动(每人只能抽取一次),盲盒中都随机放入一个杭州亚运会吉祥物,分别是“琮琮”“宸宸”“莲莲”,请画树状图分析,冠军与亚军获得相同吉祥物的概率.
【解答】解:(1)列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
由表格可知,共有12种等可能的结果,其中小明同学选择A,B两项组合的结果有2种,
∴小明同学选择A,B两项组合的概率为=.
(2)将“琮琮”“宸宸”“莲莲”分别记为a,b,c,
画树状图如下:
共有9种等可能的结果,其中冠军与亚军获得相同吉祥物的结果有3种,
∴冠军与亚军获得相同吉祥物的概率为=.
21.如图,在四边形ABCD中,AD∥BC,点F,E分别在线段BC,AC上,且∠AFC=∠DEA,AC=AD.
(1)求证:DE=AF;
(2)若∠ABC=∠CDE,求证:AF2=BF CE.
【解答】证明:(1)∵AD∥BC,
∴∠ACF=∠DAC
∵∠AFC=∠DEA,AC=AD,
∴△ACF≌△DAE(AAS),
∴AF=DE;
(2)∵△ACF≌△DAE,
∴∠AFC=∠DEA,
∴∠AFB=∠DEC,
∵∠ABC=∠CDE,
∴△ABF∽△CDE,
∴=,
∴AF DE=BF CE,
∵AF=DE,
∴AF2=BF CE.
22.已知二次函数y=ax2+bx+c(a,b,c为已知数,且a≠0)与y轴的交点是(0,4).
(1)求c的值.
(2)若二次函数y=ax2+bx+c与一次函数y=x﹣2的图象交于点(k,0),求k的值,并用含a的代数式表示b.
(3)在(2)成立的情况下,若1≤a≤2,当1≤x≤2时,y=ax2+bx+c的最大值为m,最小值为n,求m﹣n的最小值.
【解答】解:(1)把(0,4)代入y=ax2+bx+c,即c=4.
(2)由题意知点(k,0)过一次函数y=x﹣2,则k=2,
由(1)知二次函数为:y=ax2+bx+4,
∵(2,0)在二次函数y=ax2+bx+4上,
∴a×22+b×2+4=0,则b=﹣2a﹣2;
(3)由(2)知二次函数为:y=ax2﹣(2a+2)x+4,则函数对称轴为,
∵1≤a≤2,
∴,
∴,
∵1≤x≤2时,y=ax2﹣(2a+2)x+4的最大值为m,最小值为n,
∴m=a×12﹣(2a+2)×1+4=﹣a+2,,
则,
∵a=2,,
∴m﹣n的最小值为.
23.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.
素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1 确定桥拱形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2 探究悬挂范围 在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3 拟定设计方案 给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
【解答】解:任务1:
以拱顶为原点,建立如图1所示的直角坐标系,则顶点为(0,0),且过点B(10,﹣5),
设抛物线的解析式为:y=ax2,
把点B(10,﹣5)代入得:100a=﹣5,
∴a=﹣,
∴抛物线的函数表达式为:y=﹣x2;
任务2:
∵该河段水位再涨1.8m达到最高,灯笼底部距离水面不小于1m,灯笼长0.4m,
∴当悬挂点的纵坐标y≥﹣5+1.8+1+0.4=﹣1.8,
即悬挂点的纵坐标的最小值是﹣1.8m,
当y=﹣1.8时,﹣x2=﹣1.8,
∴x=±6,
∴悬挂点的横坐标的取值范围是:﹣6≤x≤6;
任务3:
方案一:如图2(坐标轴的横轴),从顶点处开始悬挂灯笼,
∵﹣6≤x≤6,相邻两盏灯笼悬挂点的水平间距均为1.6m,
∴若顶点一侧悬挂4盏灯笼时,1.6×4>6,
若顶点一侧悬挂3盏灯笼时,1.6×3<6,
∴顶点一侧最多悬挂3盏灯笼,
∵灯笼挂满后成轴对称分布,
∴共可挂7盏灯笼,
∴最左边一盏灯笼的横坐标为:﹣1.6×3=﹣4.8;
方案二:如图3,
∵若顶点一侧悬挂5盏灯笼时,0.8+1.6×(5﹣1)>6,
若顶点一侧悬挂4盏灯笼时,0.8+1.6×(4﹣1)<6,
∴顶点一侧最多悬挂4盏灯笼,
∵灯笼挂满后成轴对称分布,
∴共可挂8盏灯笼,
∴最左边一盏灯笼的横坐标为:﹣0.8﹣1.6×3=﹣5.6.
24.如图1,已知AB为⊙O的直径,弦CD⊥AB于点E,G是上一点,连结AD,AG,DG.
(1)求证:∠AGD=∠ADC;
(2)如图2,延长AG,DC相交于点F,连结CG.
①已知AG=6,GF=4,求AD的长;
②记DG与AB的交点为P,若AB=10,CD=8,当AG=AP时,求的值.
【解答】(1)证明:∵AB是⊙O直径,AB⊥CD,
∴=,
∴∠AGD=∠ADC;
(2)解:∵∠AGD=∠ADC,∠DAG=∠FAD,
∴△DAG∽△FAD,
∴,
∴AD2=AG×AF=6×(6+4)=60,
∴AD=2;
②连接OD.BD,BC,如图:
∵AB是⊙O直径,AB⊥CD,
∴DE=CE=CD=4.
∵OA=OB=OD=5,
∴OE=3.
∴BE=OB=OE=2,
∴BC===2,
∵AP=AG,
∴∠AGP=∠APG=∠DBA=∠DPB,
∴DP=DB,
∵AB⊥CD,
∴PE=BE=2,DC平分∠BDP,
∴AG=AP=AB﹣PE﹣BE=10﹣2﹣2=6,,
∴CG=BC=2,
∵四边形ADCG是圆的内接四边形,
∴∠CGF=∠ADC,∠GCF=∠DAG,
由(1)可知∠AGD=∠ADC,
∴∠CGF=∠AGD,
∴△CGF∽△AGD,
∴===.
同课章节目录
