第五章 二元一次方程组 练习题(含答案) 2024-2025学年北师大版八年级数学上册
文档属性
| 名称 | 第五章 二元一次方程组 练习题(含答案) 2024-2025学年北师大版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览


文档简介
第五章 二元一次方程组 练习题 2024-2025学年北师大版八年级数学上册
一、单选题
1.二元一次方程组的解是( )
A. B. C. D.
2.已知长江比黄河长836千米,黄河长度的6倍比长江长度的5倍多1284千米.设长江、黄河的长分别是x千米,y千米,则下列方程组中正确的是( )
A. B.
C. D.
3.在方程组中,①②,得( )
A. B. C. D.
4.校园举行足球比赛,胜一场得3分,平一场得1分,输一场得0分;七年一班共进行了12场比赛,获得19分,则七年一班获胜的场数有几种情况( )
A.1种 B.2种 C.3种 D.4种
5.一个正整数N的各位数字不全相等,且都不为0,现要将N的各位数字重新排列,可得到一个最大数和一个最小数,此最大数与最小数的和记为N的“和数”;此最大数与最小数的差记为N的“差数”。例如,245的“和数”为542+245=787;245的“差数”为542-245=297。一个四位数M,其中千位数字和百位数字均为a,十位数字为1,个位数字为b(且a≥1,b≥1),若它的“和数”是6666,则M的“差数”的值为( )
A.3456或3996 B.4356或3996 C.3456或3699 D.4356或3699
6.已知关于x,y的方程组 ,给出下列结论:① 是方程组的一个解;②当 时,x,y的值互为相反数;③当 时,方程组的解也是方程 的解;④x,y间的数量关系是 .其中正确的是( )
A.②③ B.①②③ C.②③④ D.①②③④
7.小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,其中 ,则他探究这7条直线的交点个数最多是( )
A.17个 B.18个 C.19个 D.21个
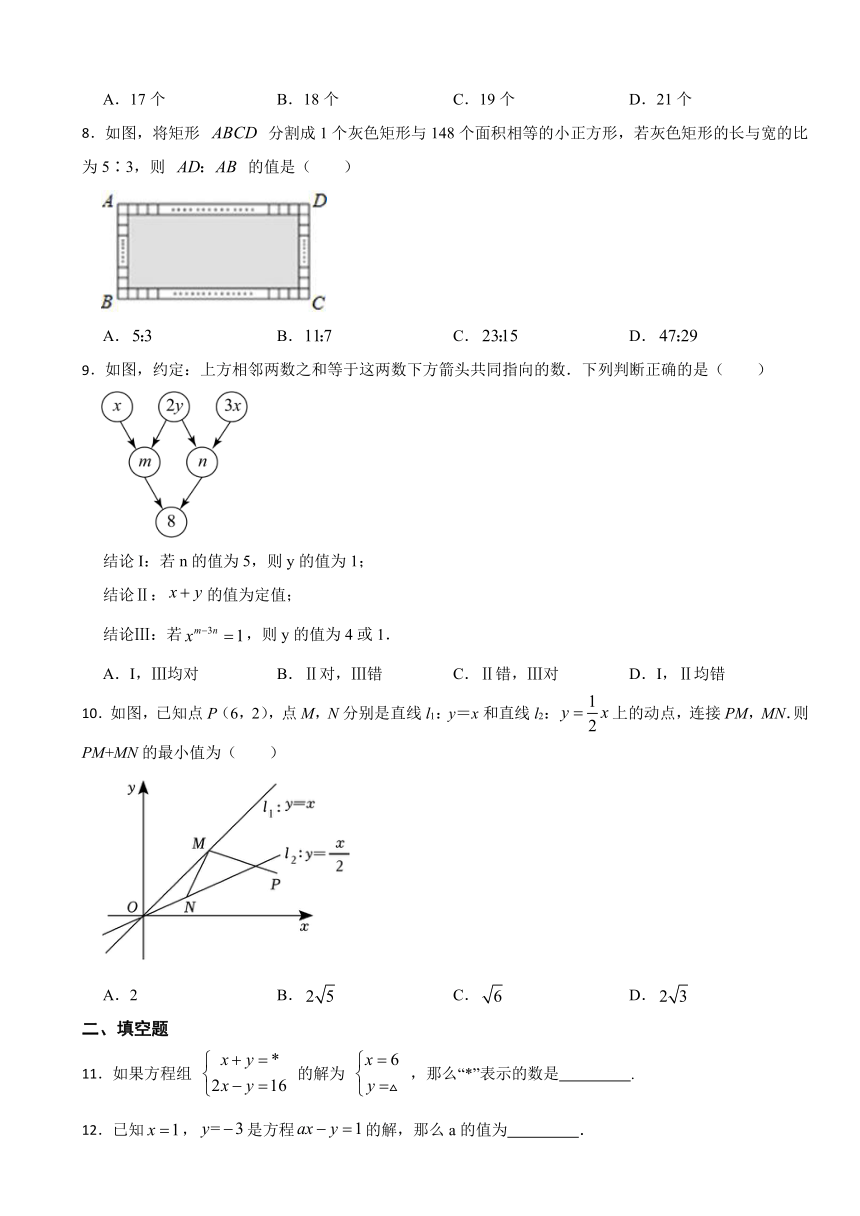
8.如图,将矩形 分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形的长与宽的比为5∶3,则 的值是( )
A. B. C. D.
9.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.下列判断正确的是( )
结论I:若n的值为5,则y的值为1;
结论Ⅱ:的值为定值;
结论Ⅲ:若,则y的值为4或1.
A.I,Ⅲ均对 B.Ⅱ对,Ⅲ错 C.Ⅱ错,Ⅲ对 D.I,Ⅱ均错
10.如图,已知点P(6,2),点M,N分别是直线l1:y=x和直线l2:上的动点,连接PM,MN.则PM+MN的最小值为( )
A.2 B. C. D.
二、填空题
11.如果方程组 的解为 ,那么“*”表示的数是 .
12.已知,是方程的解,那么a的值为 .
13.为进一步落实中共中央、国务院《关于全面加强新时代大中小学劳动教育意见》精神,某中学启动了云端农场项目制学习劳动教育课程.据调查,七年级有甲、乙、丙三个班种植辣椒(每窝里种植两株辣椒),甲班、乙班共有40株辣椒,但甲班种植的辣椒株数比乙班少,丙班有20株辣椒,已知丙班平均每株辣椒可结辣椒数量是乙班平均每株辣椒可结辣椒数量的两倍,甲班平均每株辣椒可结辣椒数量比乙班平均每株辣椒可结辣椒数量多5个,若该年级甲、乙、丙三班的平均每株辣椒可结辣椒数量恰好是甲班平均每株辣椒可结辣椒数量的,且各班平均每株辣椒可结辣椒数量均为正整数,则甲、乙、丙三班共收获辣椒 个.
14.小红去花店购买鲜花,若买 5 枝玫瑰和 3 枝百合,则她所带的钱还剩下 10 元;若买 3 枝玫瑰和 5 枝百合,则她所带的钱还缺 4 元.若设玫瑰和百合的单价分别为每枝 x,y 元, 则y-x= .
15.方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”
译文为:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问每头牛、每只羊各值金多少两”.若设每头牛值金x两,每只羊值金y两,则可列方程组为 .
16.若关于x,y的方程组的解是是,则关于x、y的方程组的解是 (用含m,n的代数式表示).
17.已知点 C、D是线段AB上两点(不与端点A、B重合),点A、B、C、D四点组成的所有线段的长度都是正整数,且总和为29,则线段AB的长度为 .
三、解答题
18.若方程组的解满足,求m的值?
19.某专卖店有A,B两种商品.已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元;A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,计算打了多少折?
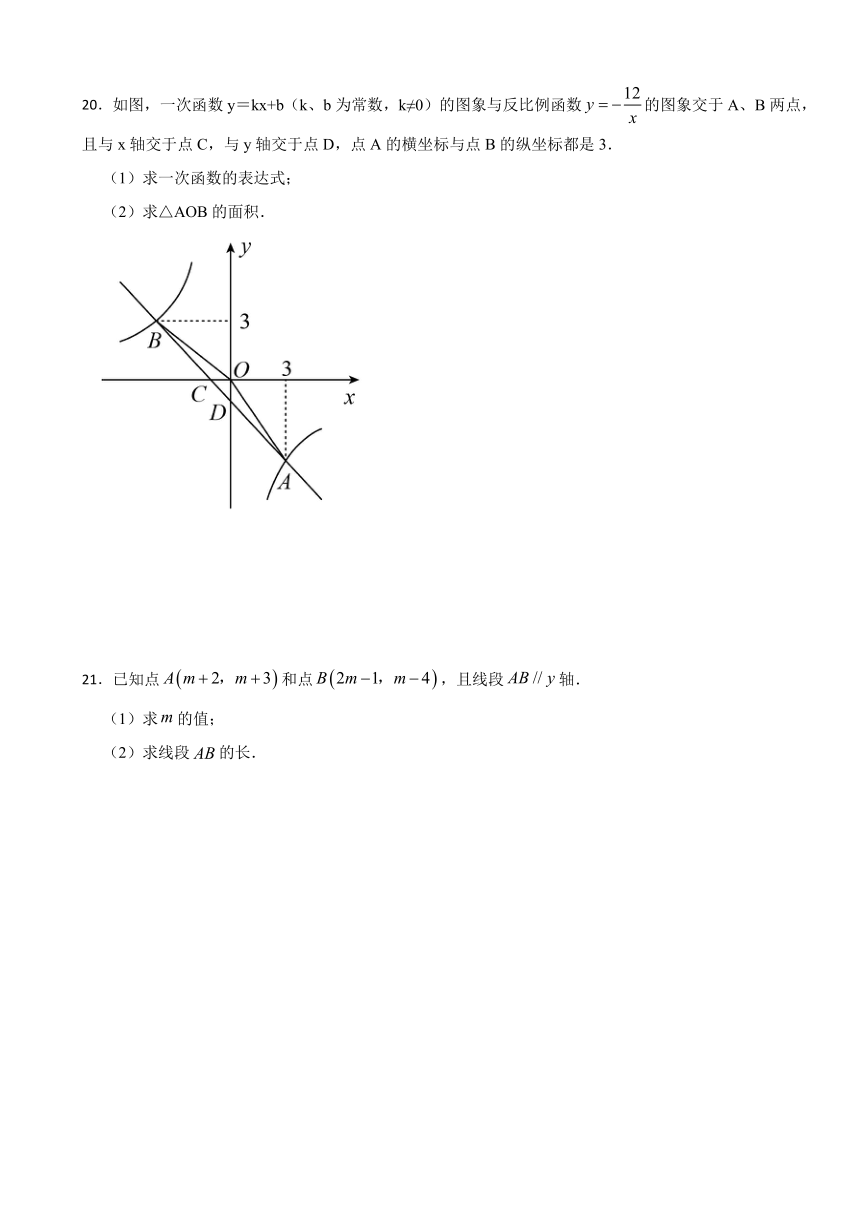
20.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,点A的横坐标与点B的纵坐标都是3.
(1)求一次函数的表达式;
(2)求△AOB的面积.
21.已知点和点,且线段轴.
(1)求的值;
(2)求线段的长.
22.某商店经营2023杭州亚运会吉祥物“宸宸、琮琮和莲莲”钥匙扣礼盒装,销售10套A型和20套B型礼盒的利润和为400元,销售20套A型和10套B型礼盒的利润和为350元.
(1)分别求销售每套A型礼盒和B型礼盒的利润.
(2)该商店计划一次性购进两种型号的礼盒共100套,其中B型礼盒的进货量不超过A型礼盒的2倍,设购进A型礼盒x套,全部售出这100套礼盒的总利润为y元.
①求y关于x的函数表达式.
②该商店购进A型、B型礼盒各多少套,才能使总利润最大?最大利润是多少?
23.如图,在平面直角坐标系中,直线分别交x、y轴于点A、B,将正比例函数的图像沿y轴向下平移3个单位长度得到直线l,直线l分别交x、y轴于点C、D,交直线于点E.
(1)直线l对应的函数表达式是__________,点E的坐标是__________;
(2)在直线上存在点F(不与点E重合),使,求点F的坐标;
(3)在x轴上是否存在点P,使?若存在,求点P的坐标;若不存在,请说明理由.
24. 设两个不同的一次函数y1=ax+b,y2=bx+a(a,b是常数,且ab≠0).
(1)若函数y1的图象经过点(2,1),且函数y2的图象经过点(1,2),求a,b的值.
(2)写出一组a,b的值,使函数y1,y2图象的交点在第四象限,并说明理由.
(3)已知a=1,b=-1,点A(p,m)在函数y1的图象上,点B(q,n)在函数y2的图象上,若p+q=2,判断m和n的大小关系.
答案解析部分
1.C
2.C
3.C
4.C
5.B
6.B
7.B
8.D
9.B
10.B
11.2
12.
13.450
14.7
15.
16.
17.8或9
18.
19.打了八折
20.(1)y=x1;(2)
21.(1)解:点和点,且线段轴,
,
解得:
(2)解:由知,;
,,
22.(1)解:设A型礼盒的利润为a元,B型礼盒的利润为b元.由题意得:
解得
答:每套A型礼盒的利润为10元,每套B型礼盒的利润为15元.
(2)解:①∵购进A型礼盒x套.
∴购进B型礼盒套.
∴.
∵
∴
②∵,y随x的增大而减少.
∵x为正整数.
∴当时,y取到最大值.
(元).
答:该商店购进A型34套、B型礼盒66套时,才能使总利润最大,为1330元.
23.(1),;(2)存在,;(3)或
24.(1)解:由题意得
解得,
故.
(2)解:(答案不唯一),理由如下,
令,解得,
函数和的图象的交点的横坐标为1,
交点坐标为(1,a+b).
若交点在第四象限,则需要,
可以取.
(3)解:若,则,
点在函数的图象上,点在函数的图备上,
①可变形为,整理得③,
③-②,得.
一、单选题
1.二元一次方程组的解是( )
A. B. C. D.
2.已知长江比黄河长836千米,黄河长度的6倍比长江长度的5倍多1284千米.设长江、黄河的长分别是x千米,y千米,则下列方程组中正确的是( )
A. B.
C. D.
3.在方程组中,①②,得( )
A. B. C. D.
4.校园举行足球比赛,胜一场得3分,平一场得1分,输一场得0分;七年一班共进行了12场比赛,获得19分,则七年一班获胜的场数有几种情况( )
A.1种 B.2种 C.3种 D.4种
5.一个正整数N的各位数字不全相等,且都不为0,现要将N的各位数字重新排列,可得到一个最大数和一个最小数,此最大数与最小数的和记为N的“和数”;此最大数与最小数的差记为N的“差数”。例如,245的“和数”为542+245=787;245的“差数”为542-245=297。一个四位数M,其中千位数字和百位数字均为a,十位数字为1,个位数字为b(且a≥1,b≥1),若它的“和数”是6666,则M的“差数”的值为( )
A.3456或3996 B.4356或3996 C.3456或3699 D.4356或3699
6.已知关于x,y的方程组 ,给出下列结论:① 是方程组的一个解;②当 时,x,y的值互为相反数;③当 时,方程组的解也是方程 的解;④x,y间的数量关系是 .其中正确的是( )
A.②③ B.①②③ C.②③④ D.①②③④
7.小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,其中 ,则他探究这7条直线的交点个数最多是( )
A.17个 B.18个 C.19个 D.21个
8.如图,将矩形 分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形的长与宽的比为5∶3,则 的值是( )
A. B. C. D.
9.如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.下列判断正确的是( )
结论I:若n的值为5,则y的值为1;
结论Ⅱ:的值为定值;
结论Ⅲ:若,则y的值为4或1.
A.I,Ⅲ均对 B.Ⅱ对,Ⅲ错 C.Ⅱ错,Ⅲ对 D.I,Ⅱ均错
10.如图,已知点P(6,2),点M,N分别是直线l1:y=x和直线l2:上的动点,连接PM,MN.则PM+MN的最小值为( )
A.2 B. C. D.
二、填空题
11.如果方程组 的解为 ,那么“*”表示的数是 .
12.已知,是方程的解,那么a的值为 .
13.为进一步落实中共中央、国务院《关于全面加强新时代大中小学劳动教育意见》精神,某中学启动了云端农场项目制学习劳动教育课程.据调查,七年级有甲、乙、丙三个班种植辣椒(每窝里种植两株辣椒),甲班、乙班共有40株辣椒,但甲班种植的辣椒株数比乙班少,丙班有20株辣椒,已知丙班平均每株辣椒可结辣椒数量是乙班平均每株辣椒可结辣椒数量的两倍,甲班平均每株辣椒可结辣椒数量比乙班平均每株辣椒可结辣椒数量多5个,若该年级甲、乙、丙三班的平均每株辣椒可结辣椒数量恰好是甲班平均每株辣椒可结辣椒数量的,且各班平均每株辣椒可结辣椒数量均为正整数,则甲、乙、丙三班共收获辣椒 个.
14.小红去花店购买鲜花,若买 5 枝玫瑰和 3 枝百合,则她所带的钱还剩下 10 元;若买 3 枝玫瑰和 5 枝百合,则她所带的钱还缺 4 元.若设玫瑰和百合的单价分别为每枝 x,y 元, 则y-x= .
15.方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”
译文为:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问每头牛、每只羊各值金多少两”.若设每头牛值金x两,每只羊值金y两,则可列方程组为 .
16.若关于x,y的方程组的解是是,则关于x、y的方程组的解是 (用含m,n的代数式表示).
17.已知点 C、D是线段AB上两点(不与端点A、B重合),点A、B、C、D四点组成的所有线段的长度都是正整数,且总和为29,则线段AB的长度为 .
三、解答题
18.若方程组的解满足,求m的值?
19.某专卖店有A,B两种商品.已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元;A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,计算打了多少折?
20.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,点A的横坐标与点B的纵坐标都是3.
(1)求一次函数的表达式;
(2)求△AOB的面积.
21.已知点和点,且线段轴.
(1)求的值;
(2)求线段的长.
22.某商店经营2023杭州亚运会吉祥物“宸宸、琮琮和莲莲”钥匙扣礼盒装,销售10套A型和20套B型礼盒的利润和为400元,销售20套A型和10套B型礼盒的利润和为350元.
(1)分别求销售每套A型礼盒和B型礼盒的利润.
(2)该商店计划一次性购进两种型号的礼盒共100套,其中B型礼盒的进货量不超过A型礼盒的2倍,设购进A型礼盒x套,全部售出这100套礼盒的总利润为y元.
①求y关于x的函数表达式.
②该商店购进A型、B型礼盒各多少套,才能使总利润最大?最大利润是多少?
23.如图,在平面直角坐标系中,直线分别交x、y轴于点A、B,将正比例函数的图像沿y轴向下平移3个单位长度得到直线l,直线l分别交x、y轴于点C、D,交直线于点E.
(1)直线l对应的函数表达式是__________,点E的坐标是__________;
(2)在直线上存在点F(不与点E重合),使,求点F的坐标;
(3)在x轴上是否存在点P,使?若存在,求点P的坐标;若不存在,请说明理由.
24. 设两个不同的一次函数y1=ax+b,y2=bx+a(a,b是常数,且ab≠0).
(1)若函数y1的图象经过点(2,1),且函数y2的图象经过点(1,2),求a,b的值.
(2)写出一组a,b的值,使函数y1,y2图象的交点在第四象限,并说明理由.
(3)已知a=1,b=-1,点A(p,m)在函数y1的图象上,点B(q,n)在函数y2的图象上,若p+q=2,判断m和n的大小关系.
答案解析部分
1.C
2.C
3.C
4.C
5.B
6.B
7.B
8.D
9.B
10.B
11.2
12.
13.450
14.7
15.
16.
17.8或9
18.
19.打了八折
20.(1)y=x1;(2)
21.(1)解:点和点,且线段轴,
,
解得:
(2)解:由知,;
,,
22.(1)解:设A型礼盒的利润为a元,B型礼盒的利润为b元.由题意得:
解得
答:每套A型礼盒的利润为10元,每套B型礼盒的利润为15元.
(2)解:①∵购进A型礼盒x套.
∴购进B型礼盒套.
∴.
∵
∴
②∵,y随x的增大而减少.
∵x为正整数.
∴当时,y取到最大值.
(元).
答:该商店购进A型34套、B型礼盒66套时,才能使总利润最大,为1330元.
23.(1),;(2)存在,;(3)或
24.(1)解:由题意得
解得,
故.
(2)解:(答案不唯一),理由如下,
令,解得,
函数和的图象的交点的横坐标为1,
交点坐标为(1,a+b).
若交点在第四象限,则需要,
可以取.
(3)解:若,则,
点在函数的图象上,点在函数的图备上,
①可变形为,整理得③,
③-②,得.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
