26.2.3求二次函数的表达式 同步练习(含答案)
文档属性
| 名称 | 26.2.3求二次函数的表达式 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 262.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
26.2.3求二次函数的表达式
一、填空题
1.请写出一个开口向下,经过原点的二次函数的表达式 .
2.请写出一个开口向下且经过原点的抛物线解析式 .
3.我们已学过用待定系数法求一次函数的表达式.类似地,我们也可以用待定系数法求二次函数y=ax2+bx+c的表达式.当需要确定的系数有3个时,需要将3对自变量和函数的对应值代入表达式,获取三元一次方程组.而当其中一个系数已知时,只需要将 对自变量与函数的对应值代入表达式,获取 方程组求解.
4.如图,抛物线与直线交于A、B两点,其中点A在y轴上,点B坐标为,点P为y轴左侧的抛物线上一动点,过点P作轴于点C,交于点D.当点P运动到直线下方某一处时,过点P作,垂足为M,连接,使为等腰直角三角形,请直接写出此时点P的坐标为 .
5.第 19届亚洲运动会于2023年9月23日在浙江杭州举行了开幕式,受到了全世界人民的关注.中国某 天才跳水运动员从起跳至入水的运动路线可以看作是抛物线的一部分,如图所示,该运动员起点A 距离水面,运动过程中的最高点B 距水面.与点A的水平距离为(其他相关数据见图中标注).根据上述信息,可推断出入水点C 与池边的水平距离为 m.
6.将抛物线绕原点旋转,则得到的抛物线的函数表达式为 .
二、单选题
7.二次函数的图象的顶点坐标是,且图象与轴交于点.将二次函数的图象以轴为对称轴进行折叠,则折叠后得到的函数解析式为( )
A. B.
C. D.
8.二次函数的图象的最高点坐标是,则的值分别是( )
A.2,4 B. C. D.
9.二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y= (x﹣2)2+3 B.y= (x﹣2)2﹣3
C.y=﹣ (x﹣2)2+3 D.y=﹣ (x﹣2)2﹣3
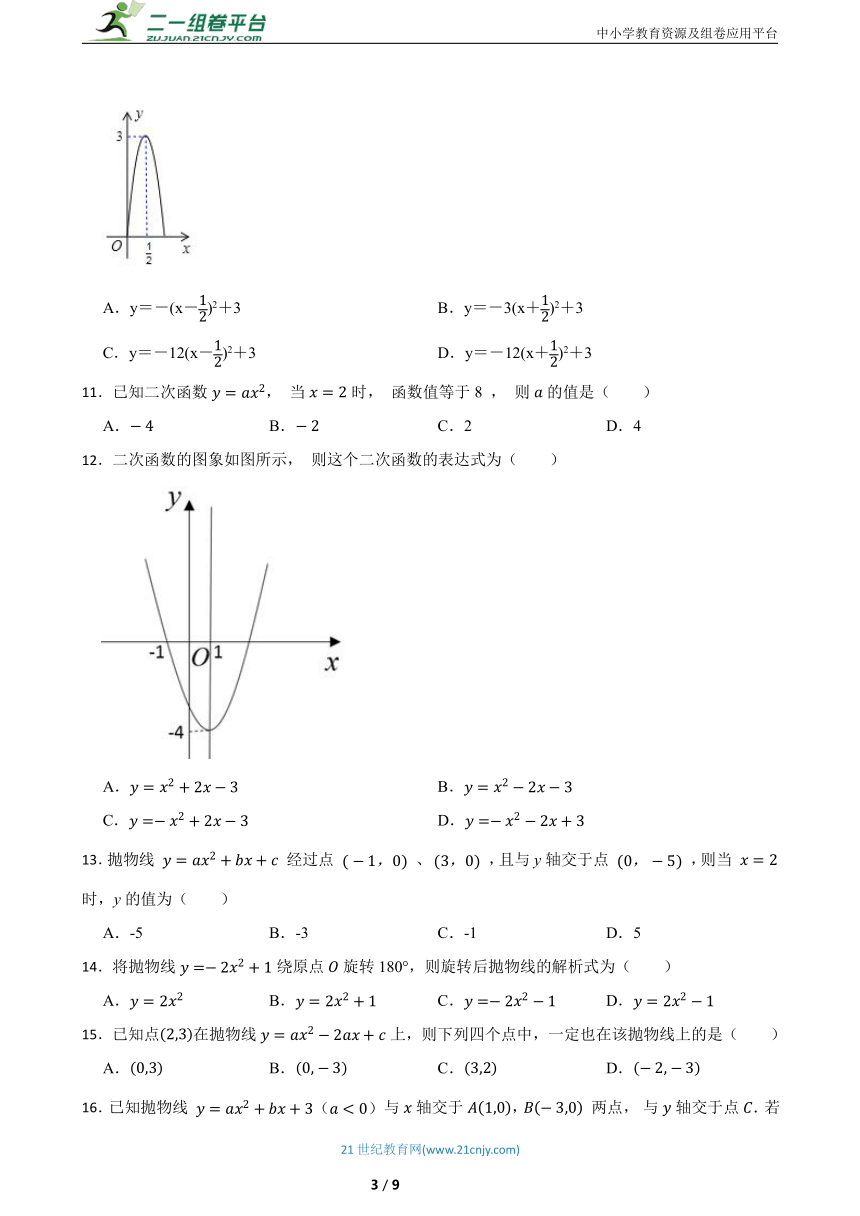
10.西宁中心广场有各种音乐喷泉,其中一个喷水管的最大高度为3米,此时距喷水管的水平距离为米,在如图所示的坐标系中,这个喷泉的函数关系式是()
A.y=-(x-)2+3 B.y=-3(x+)2+3
C.y=-12(x-)2+3 D.y=-12(x+)2+3
11.已知二次函数, 当时, 函数值等于8 , 则的值是( )
A. B. C.2 D.4
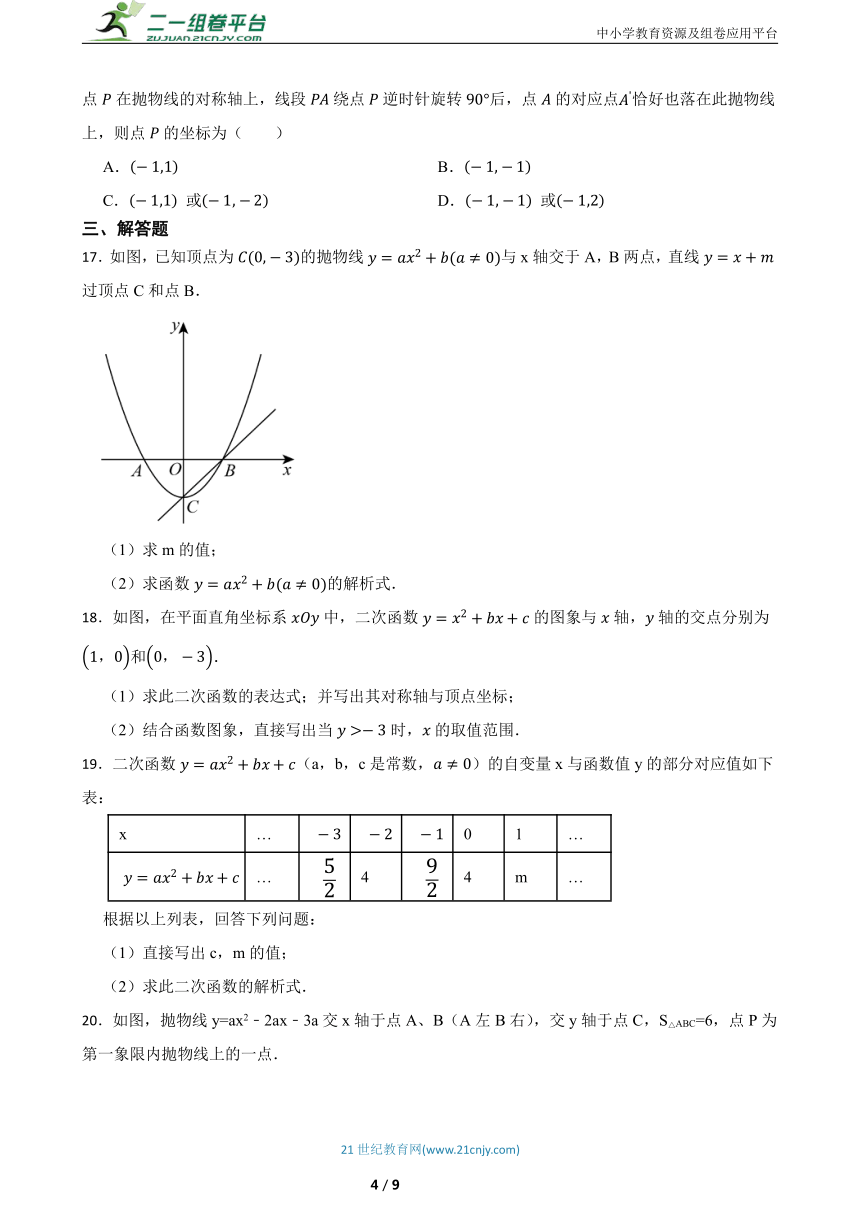
12.二次函数的图象如图所示, 则这个二次函数的表达式为( )
A. B.
C. D.
13.抛物线 经过点 、 ,且与y轴交于点 ,则当 时,y的值为( )
A.-5 B.-3 C.-1 D.5
14.将抛物线绕原点旋转180°,则旋转后抛物线的解析式为( )
A. B. C. D.
15.已知点在抛物线上,则下列四个点中,一定也在该抛物线上的是( )
A. B. C. D.
16.已知抛物线 与轴交于, 两点, 与轴交于点.若点在抛物线的对称轴上,线段绕点逆时针旋转后,点的对应点恰好也落在此抛物线上,则点的坐标为( )
A. B.
C. 或 D. 或
三、解答题
17.如图,已知顶点为的抛物线与x轴交于A,B两点,直线过顶点C和点B.
(1)求m的值;
(2)求函数的解析式.
18.如图,在平面直角坐标系中,二次函数的图象与轴,轴的交点分别为和.
(1)求此二次函数的表达式;并写出其对称轴与顶点坐标;
(2)结合函数图象,直接写出当时,的取值范围.
19.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x … 0 1 …
… 4 4 m …
根据以上列表,回答下列问题:
(1)直接写出c,m的值;
(2)求此二次函数的解析式.
20.如图,抛物线y=ax2﹣2ax﹣3a交x轴于点A、B(A左B右),交y轴于点C,S△ABC=6,点P为第一象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)若∠PCB=45°,求点P的坐标;
(3)点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、AQ,当PC= AQ时,求点P的坐标以及△PCQ的面积.
四、计算题
21.如图,抛物线与x轴交于A,两点,与y轴交于点C,对称轴为直线
(1)求抛物线的解析式及顶点坐标;
(2)点和点是抛物线上两点,且,求c的取值范围.
22.如图1,已知直线与x轴、y轴分别交于B,C两点,抛物线经过点B,C交x轴于另一点A,点P为x轴上方抛物线上一动点(不与点C重合),设点P横坐标为m.
(1)填空:B(___,___),C(___,___),抛物线的解析式为______;
(2)过点P作轴,交直线于点M,当时,求点P的横坐标;
(3)过点P作x轴的平行线交直线于点Q,线段的长记为d,求d关于m的函数.
23.已知在平面直角坐标系中,原点O是正方形的对角线交点,点,过x轴正半轴上的动点作x轴垂线交过点B,C两点的抛物线于点Q(其中C为抛物线的顶点).
(1)求抛物线的解析式;
(2)是否存在四边形为菱形,若存在,求出m值;若不在,说明理由.
答案解析部分
1.【答案】答案不唯一( ,任何a<0,c=0的二次函数均可)
【知识点】待定系数法求二次函数解析式
2.【答案】y=-x2
【知识点】待定系数法求二次函数解析式
3.【答案】两;二元一次
【知识点】待定系数法求二次函数解析式
4.【答案】
【知识点】待定系数法求二次函数解析式;余角、补角及其性质
5.【答案】4
【知识点】待定系数法求二次函数解析式
6.【答案】
【知识点】待定系数法求二次函数解析式;旋转的性质
7.【答案】B
【知识点】待定系数法求二次函数解析式;坐标与图形变化﹣对称
8.【答案】D
【知识点】待定系数法求二次函数解析式
9.【答案】C
【知识点】待定系数法求二次函数解析式
10.【答案】C
【知识点】待定系数法求二次函数解析式
11.【答案】C
【知识点】待定系数法求二次函数解析式
12.【答案】B
【知识点】待定系数法求二次函数解析式
13.【答案】A
【知识点】待定系数法求二次函数解析式
14.【答案】D
【知识点】待定系数法求二次函数解析式;旋转的性质
15.【答案】A
【知识点】待定系数法求二次函数解析式
16.【答案】C
【知识点】待定系数法求二次函数解析式;旋转的性质
17.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式
18.【答案】(1)表达式为,对称轴为直线,顶点坐标为
(2)或
【知识点】待定系数法求二次函数解析式
19.【答案】(1),;(2)或
【知识点】待定系数法求二次函数解析式
20.【答案】(1)解:∵抛物线y=ax2﹣2ax﹣3a=a(x+1)(x﹣3),
∴A(﹣1,0),B(3,0),C(0,﹣3a),
∴AB=4,OC=|﹣3a|=|3a|,
∵S△ABC=6,
∴ AB OC=6,
∴ ×4×|3a|=6,
∴a=﹣1或a=1(舍),
∴抛物线的解析式为y=﹣x2+2x+3
(2)解:由(1)知,B(3,0),C(0,﹣3a),∴C(0,3),∴OB=3,OC=3,∴△OBC是等腰直角三角形,∴∠BCO=∠OBC=45°,
∵点P为第一象限内抛物线上的一点,且∠PCB=45°,
∴PC∥OB,∴P点的纵坐标为3,
由(1)知,抛物线的解析式为y=﹣x2+2x+3,
令y=3,∴﹣x2+2x+3=3,∴x=0(舍)或x=2,∴P(2,3)
(3)解:如图2,过点P作PD⊥x轴交CQ于D,设P(3﹣m,﹣m2+4m)(0<m<1);∵C(0,3),∴PC2=(3﹣m)2+(﹣m2+4m﹣3)2=(m﹣3)2[(m﹣1)2+1],∵点Q的横坐标比点P的横坐标大1,∴Q(4﹣m,﹣m2+6m﹣5),∵A(﹣1,0).∴AQ2=(4﹣m+1)2+(﹣m2+6m﹣5)2=(m﹣5)2[(m﹣1)2+1]∵PC= AQ,∴81PC2=25AQ2,∴81(m﹣3)2[(m﹣1)2+1]=25(m﹣5)2[(m﹣1)2+1],∵0<m<1,∴[(m﹣1)2+1]≠0,∴81(m﹣3)2=25(m﹣5)2,∴9(m﹣3)=±5(m﹣5),∴m= 或m= (舍),∴P( , ),Q( ,﹣ ),∵C(0,3),∴直线CQ的解析式为y=﹣ x+3,∵P( , ),∴D( ,﹣ ),∴PD= + = ,
∴S△PCQ=S△PCD+S△PQD== PD×xP+= PD×(xQ﹣xP)== PD×xQ== × × = .
【知识点】待定系数法求二次函数解析式
21.【答案】(1)抛物线的解析式为,抛物线的顶点坐标为
(2)
【知识点】待定系数法求二次函数解析式
22.【答案】(1)3,0,0,3,
(2)点P的横坐标为:1或2或
(3)
【知识点】二次函数图象与系数的关系;待定系数法求二次函数解析式;一次函数图象与坐标轴交点问题
23.【答案】(1)
(2)
【知识点】待定系数法求二次函数解析式;勾股定理;菱形的性质;正方形的性质
21世纪教育网(www.21cnjy.com)
9 / 9
26.2.3求二次函数的表达式
一、填空题
1.请写出一个开口向下,经过原点的二次函数的表达式 .
2.请写出一个开口向下且经过原点的抛物线解析式 .
3.我们已学过用待定系数法求一次函数的表达式.类似地,我们也可以用待定系数法求二次函数y=ax2+bx+c的表达式.当需要确定的系数有3个时,需要将3对自变量和函数的对应值代入表达式,获取三元一次方程组.而当其中一个系数已知时,只需要将 对自变量与函数的对应值代入表达式,获取 方程组求解.
4.如图,抛物线与直线交于A、B两点,其中点A在y轴上,点B坐标为,点P为y轴左侧的抛物线上一动点,过点P作轴于点C,交于点D.当点P运动到直线下方某一处时,过点P作,垂足为M,连接,使为等腰直角三角形,请直接写出此时点P的坐标为 .
5.第 19届亚洲运动会于2023年9月23日在浙江杭州举行了开幕式,受到了全世界人民的关注.中国某 天才跳水运动员从起跳至入水的运动路线可以看作是抛物线的一部分,如图所示,该运动员起点A 距离水面,运动过程中的最高点B 距水面.与点A的水平距离为(其他相关数据见图中标注).根据上述信息,可推断出入水点C 与池边的水平距离为 m.
6.将抛物线绕原点旋转,则得到的抛物线的函数表达式为 .
二、单选题
7.二次函数的图象的顶点坐标是,且图象与轴交于点.将二次函数的图象以轴为对称轴进行折叠,则折叠后得到的函数解析式为( )
A. B.
C. D.
8.二次函数的图象的最高点坐标是,则的值分别是( )
A.2,4 B. C. D.
9.二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y= (x﹣2)2+3 B.y= (x﹣2)2﹣3
C.y=﹣ (x﹣2)2+3 D.y=﹣ (x﹣2)2﹣3
10.西宁中心广场有各种音乐喷泉,其中一个喷水管的最大高度为3米,此时距喷水管的水平距离为米,在如图所示的坐标系中,这个喷泉的函数关系式是()
A.y=-(x-)2+3 B.y=-3(x+)2+3
C.y=-12(x-)2+3 D.y=-12(x+)2+3
11.已知二次函数, 当时, 函数值等于8 , 则的值是( )
A. B. C.2 D.4
12.二次函数的图象如图所示, 则这个二次函数的表达式为( )
A. B.
C. D.
13.抛物线 经过点 、 ,且与y轴交于点 ,则当 时,y的值为( )
A.-5 B.-3 C.-1 D.5
14.将抛物线绕原点旋转180°,则旋转后抛物线的解析式为( )
A. B. C. D.
15.已知点在抛物线上,则下列四个点中,一定也在该抛物线上的是( )
A. B. C. D.
16.已知抛物线 与轴交于, 两点, 与轴交于点.若点在抛物线的对称轴上,线段绕点逆时针旋转后,点的对应点恰好也落在此抛物线上,则点的坐标为( )
A. B.
C. 或 D. 或
三、解答题
17.如图,已知顶点为的抛物线与x轴交于A,B两点,直线过顶点C和点B.
(1)求m的值;
(2)求函数的解析式.
18.如图,在平面直角坐标系中,二次函数的图象与轴,轴的交点分别为和.
(1)求此二次函数的表达式;并写出其对称轴与顶点坐标;
(2)结合函数图象,直接写出当时,的取值范围.
19.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x … 0 1 …
… 4 4 m …
根据以上列表,回答下列问题:
(1)直接写出c,m的值;
(2)求此二次函数的解析式.
20.如图,抛物线y=ax2﹣2ax﹣3a交x轴于点A、B(A左B右),交y轴于点C,S△ABC=6,点P为第一象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)若∠PCB=45°,求点P的坐标;
(3)点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、AQ,当PC= AQ时,求点P的坐标以及△PCQ的面积.
四、计算题
21.如图,抛物线与x轴交于A,两点,与y轴交于点C,对称轴为直线
(1)求抛物线的解析式及顶点坐标;
(2)点和点是抛物线上两点,且,求c的取值范围.
22.如图1,已知直线与x轴、y轴分别交于B,C两点,抛物线经过点B,C交x轴于另一点A,点P为x轴上方抛物线上一动点(不与点C重合),设点P横坐标为m.
(1)填空:B(___,___),C(___,___),抛物线的解析式为______;
(2)过点P作轴,交直线于点M,当时,求点P的横坐标;
(3)过点P作x轴的平行线交直线于点Q,线段的长记为d,求d关于m的函数.
23.已知在平面直角坐标系中,原点O是正方形的对角线交点,点,过x轴正半轴上的动点作x轴垂线交过点B,C两点的抛物线于点Q(其中C为抛物线的顶点).
(1)求抛物线的解析式;
(2)是否存在四边形为菱形,若存在,求出m值;若不在,说明理由.
答案解析部分
1.【答案】答案不唯一( ,任何a<0,c=0的二次函数均可)
【知识点】待定系数法求二次函数解析式
2.【答案】y=-x2
【知识点】待定系数法求二次函数解析式
3.【答案】两;二元一次
【知识点】待定系数法求二次函数解析式
4.【答案】
【知识点】待定系数法求二次函数解析式;余角、补角及其性质
5.【答案】4
【知识点】待定系数法求二次函数解析式
6.【答案】
【知识点】待定系数法求二次函数解析式;旋转的性质
7.【答案】B
【知识点】待定系数法求二次函数解析式;坐标与图形变化﹣对称
8.【答案】D
【知识点】待定系数法求二次函数解析式
9.【答案】C
【知识点】待定系数法求二次函数解析式
10.【答案】C
【知识点】待定系数法求二次函数解析式
11.【答案】C
【知识点】待定系数法求二次函数解析式
12.【答案】B
【知识点】待定系数法求二次函数解析式
13.【答案】A
【知识点】待定系数法求二次函数解析式
14.【答案】D
【知识点】待定系数法求二次函数解析式;旋转的性质
15.【答案】A
【知识点】待定系数法求二次函数解析式
16.【答案】C
【知识点】待定系数法求二次函数解析式;旋转的性质
17.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式
18.【答案】(1)表达式为,对称轴为直线,顶点坐标为
(2)或
【知识点】待定系数法求二次函数解析式
19.【答案】(1),;(2)或
【知识点】待定系数法求二次函数解析式
20.【答案】(1)解:∵抛物线y=ax2﹣2ax﹣3a=a(x+1)(x﹣3),
∴A(﹣1,0),B(3,0),C(0,﹣3a),
∴AB=4,OC=|﹣3a|=|3a|,
∵S△ABC=6,
∴ AB OC=6,
∴ ×4×|3a|=6,
∴a=﹣1或a=1(舍),
∴抛物线的解析式为y=﹣x2+2x+3
(2)解:由(1)知,B(3,0),C(0,﹣3a),∴C(0,3),∴OB=3,OC=3,∴△OBC是等腰直角三角形,∴∠BCO=∠OBC=45°,
∵点P为第一象限内抛物线上的一点,且∠PCB=45°,
∴PC∥OB,∴P点的纵坐标为3,
由(1)知,抛物线的解析式为y=﹣x2+2x+3,
令y=3,∴﹣x2+2x+3=3,∴x=0(舍)或x=2,∴P(2,3)
(3)解:如图2,过点P作PD⊥x轴交CQ于D,设P(3﹣m,﹣m2+4m)(0<m<1);∵C(0,3),∴PC2=(3﹣m)2+(﹣m2+4m﹣3)2=(m﹣3)2[(m﹣1)2+1],∵点Q的横坐标比点P的横坐标大1,∴Q(4﹣m,﹣m2+6m﹣5),∵A(﹣1,0).∴AQ2=(4﹣m+1)2+(﹣m2+6m﹣5)2=(m﹣5)2[(m﹣1)2+1]∵PC= AQ,∴81PC2=25AQ2,∴81(m﹣3)2[(m﹣1)2+1]=25(m﹣5)2[(m﹣1)2+1],∵0<m<1,∴[(m﹣1)2+1]≠0,∴81(m﹣3)2=25(m﹣5)2,∴9(m﹣3)=±5(m﹣5),∴m= 或m= (舍),∴P( , ),Q( ,﹣ ),∵C(0,3),∴直线CQ的解析式为y=﹣ x+3,∵P( , ),∴D( ,﹣ ),∴PD= + = ,
∴S△PCQ=S△PCD+S△PQD== PD×xP+= PD×(xQ﹣xP)== PD×xQ== × × = .
【知识点】待定系数法求二次函数解析式
21.【答案】(1)抛物线的解析式为,抛物线的顶点坐标为
(2)
【知识点】待定系数法求二次函数解析式
22.【答案】(1)3,0,0,3,
(2)点P的横坐标为:1或2或
(3)
【知识点】二次函数图象与系数的关系;待定系数法求二次函数解析式;一次函数图象与坐标轴交点问题
23.【答案】(1)
(2)
【知识点】待定系数法求二次函数解析式;勾股定理;菱形的性质;正方形的性质
21世纪教育网(www.21cnjy.com)
9 / 9
