26.2二次函数的图像和性质本节综合题(含答案)
文档属性
| 名称 | 26.2二次函数的图像和性质本节综合题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
26.2二次函数的图像和性质本节综合题
一、填空题
1.如果抛物线 经过 和 ,那么对称轴是直线 .
2.如果抛物线 有最高点,那么a的取值范围是 .
3.将抛物线y=3x2向右平移5个单位,可得到抛物线 .
4.二次函数的最大值为 ,最小值为 .
5.已知点A(x1,y1),B(x2,y2)在抛物线y=x2-3上,且0<x1<x2,则y1 y2.(填“<”或“>”或“=”)
6.二次函数 的顶点坐标是 .
二、单选题
7.将抛物线y=3x2-6x+5先向左平移4个单位长度,再向下平移2个单位长度后所得抛物线的解析式为( )
A.y=3(x-5)2+4 B.y=3(x-5)2
C.y=3(x+3)2+4 D.y=3(x+3)2
8.将抛物线向右平移个单位后,得到的抛物线的解析式是( )
A. B. C. D.
9.抛物线是由抛物线经过怎样的平移得到的( )
A.向左平移个单位长度,向上平移个单位长度
B.向左平移个单位长度,向下平移个单位长度
C.向右平移个单位长度,向上平移个单位长度
D.向右平移个单位长度,向下平移个单位长度
10.二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
A.y=x2 B.y=(x-2)2 C.y=x2+2 D.y=(x+2)2
11.已知点A(a-2b,2-4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(-3,7) B.(-1,7) C.(-4,10) D.(0,10)
三、解答题
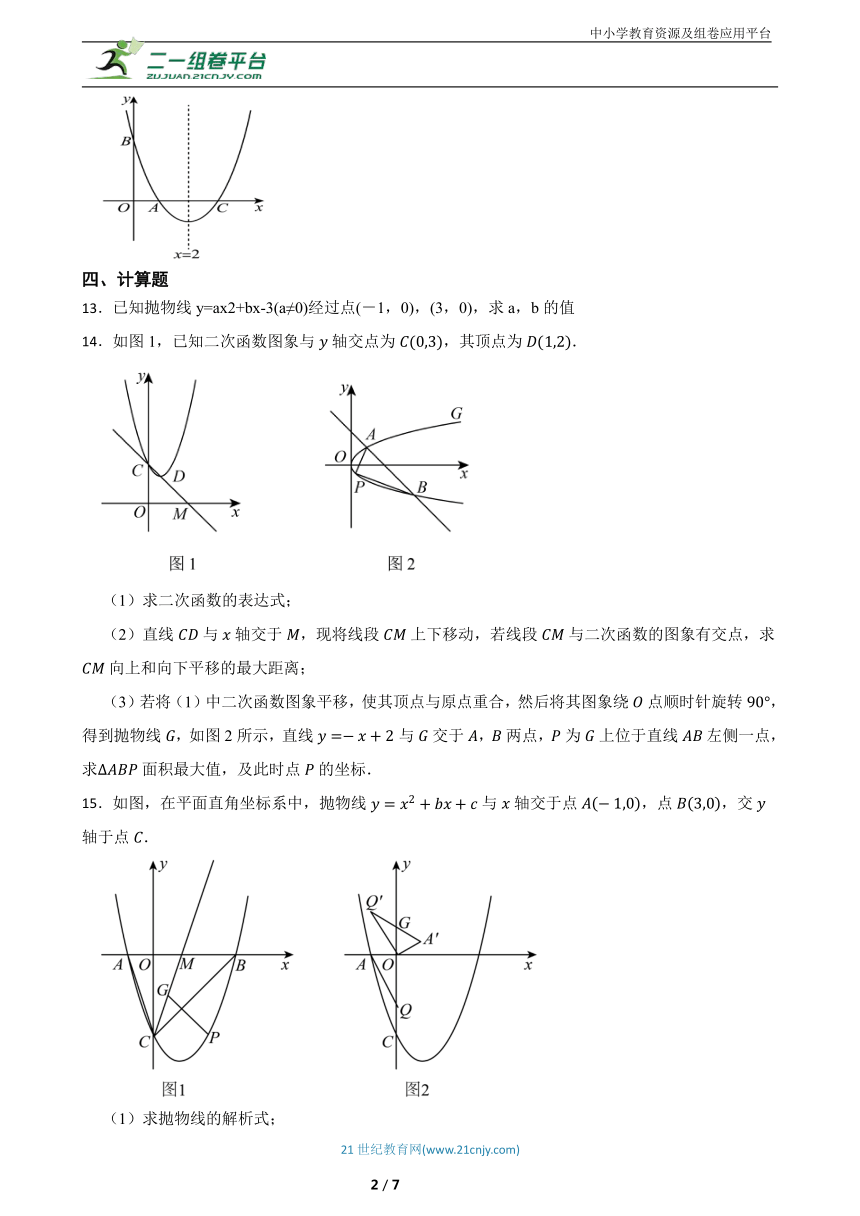
12.如图,抛物线交轴于点,交轴于点,对称轴是直线.求抛物线的解析式.
四、计算题
13.已知抛物线y=ax2+bx-3(a≠0)经过点(-1,0),(3,0),求a,b的值
14.如图1,已知二次函数图象与轴交点为,其顶点为.
(1)求二次函数的表达式;
(2)直线与轴交于,现将线段上下移动,若线段与二次函数的图象有交点,求向上和向下平移的最大距离;
(3)若将(1)中二次函数图象平移,使其顶点与原点重合,然后将其图象绕点顺时针旋转,得到抛物线,如图2所示,直线与交于,两点,为上位于直线左侧一点,求面积最大值,及此时点的坐标.
15.如图,在平面直角坐标系中,抛物线与轴交于点,点,交轴于点.
(1)求抛物线的解析式;
(2)如图,连接,过点作射线交轴的正半轴于点,点与点关于原点对称,点是第四象限抛物线上一动点,过点作的垂线交于点,求线段长度的最大值及此时点的坐标;
(3)如图,把点向上平移个单位得到点,连接,把绕点顺时针旋转一定的角度,得到,其中边交坐标轴于点,在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
五、作图题
16.已知二次函数
(1)完成下表:
(2)在下面的坐标系中描点,画出该二次函数的图象.
六、综合题
17.已知二次函数y=ax2的图象经过A(2,﹣4)
(1)求这个二次函数的解析式;
(2)请写出这个二次函数图象的顶点坐标、对称轴和开口方向.
18.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
19.如图,二次函数 的图象与y轴交于点C,点B在抛物线上,且点B与点C关于该二次函数图象的对称轴对称,已知一次函数 的图象经过该二次函数图象上点 及点B.
(1)求二次函数的解析式;
(2)根据图象,写出满足 的x的取值范围.
答案解析部分
1.【答案】x=1
【知识点】二次函数y=ax²+bx+c的性质
2.【答案】
【知识点】二次函数的最值
3.【答案】y=3(x﹣5)2
【知识点】二次函数图象的几何变换
4.【答案】16;-20
【知识点】二次函数的最值
5.【答案】<
【知识点】二次函数y=a(x-h)²+k的性质
6.【答案】(2,3)
【知识点】二次函数y=a(x-h)²+k的性质
7.【答案】D
【知识点】二次函数图象的几何变换
8.【答案】B
【知识点】二次函数图象的几何变换
9.【答案】D
【知识点】二次函数图象的几何变换
10.【答案】C
【知识点】二次函数图象的几何变换
11.【答案】D
【知识点】二次函数y=a(x-h)²+k的性质
12.【答案】
【知识点】待定系数法求二次函数解析式
13.【答案】解:∵抛物线过点(-1,0),(3,0),
∴,
解得:
∴a=1,b=-2.
【知识点】待定系数法求二次函数解析式
14.【答案】(1)
(2)CM向下平移的最大距离为,向上平移的最大距离为6.
(3)
【知识点】待定系数法求二次函数解析式;旋转的性质
15.【答案】(1)抛物线的解析式为;
(2),此时;
(3).
【知识点】待定系数法求二次函数解析式;解直角三角形;旋转的性质
16.【答案】(1)解:如下表,
x … -2 -1 0 1 2 3 4 …
y … -2 0 -2 …
(2)解:见下图,
【知识点】二次函数y=a(x-h)²+k的图象
17.【答案】(1)解:∵二次函数y=ax2的图象经过A(2,﹣4), ∴﹣4=4a,
解得a=﹣1,
∴二次函数的解析式为y=﹣x2
(2)解:∵二次函数的解析式为 y=﹣x2,
∴这个二次函数图象的顶点坐标为(0,0),对称轴为y轴,开口方向向下
【知识点】待定系数法求二次函数解析式;二次函数y=ax²的性质
18.【答案】(1)y=﹣20x2+100x+6000,0≤x<20(或0<x<20);(2)当降价2.5元时,利润最大且为6125元.
【知识点】二次函数的最值
19.【答案】(1)解: 抛物线 经过点 ,
,
,
抛物线解析式为 ;
(2)解:令 ,则 ,
点C坐标 ,
对称轴为直线 ,B、C关于对称轴对称,
点B坐标 ,
由图象可知,满足 的x的取值范围为 .
【知识点】待定系数法求二次函数解析式;二次函数y=a(x-h)²+k的性质
21世纪教育网(www.21cnjy.com)
7 / 7
26.2二次函数的图像和性质本节综合题
一、填空题
1.如果抛物线 经过 和 ,那么对称轴是直线 .
2.如果抛物线 有最高点,那么a的取值范围是 .
3.将抛物线y=3x2向右平移5个单位,可得到抛物线 .
4.二次函数的最大值为 ,最小值为 .
5.已知点A(x1,y1),B(x2,y2)在抛物线y=x2-3上,且0<x1<x2,则y1 y2.(填“<”或“>”或“=”)
6.二次函数 的顶点坐标是 .
二、单选题
7.将抛物线y=3x2-6x+5先向左平移4个单位长度,再向下平移2个单位长度后所得抛物线的解析式为( )
A.y=3(x-5)2+4 B.y=3(x-5)2
C.y=3(x+3)2+4 D.y=3(x+3)2
8.将抛物线向右平移个单位后,得到的抛物线的解析式是( )
A. B. C. D.
9.抛物线是由抛物线经过怎样的平移得到的( )
A.向左平移个单位长度,向上平移个单位长度
B.向左平移个单位长度,向下平移个单位长度
C.向右平移个单位长度,向上平移个单位长度
D.向右平移个单位长度,向下平移个单位长度
10.二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
A.y=x2 B.y=(x-2)2 C.y=x2+2 D.y=(x+2)2
11.已知点A(a-2b,2-4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(-3,7) B.(-1,7) C.(-4,10) D.(0,10)
三、解答题
12.如图,抛物线交轴于点,交轴于点,对称轴是直线.求抛物线的解析式.
四、计算题
13.已知抛物线y=ax2+bx-3(a≠0)经过点(-1,0),(3,0),求a,b的值
14.如图1,已知二次函数图象与轴交点为,其顶点为.
(1)求二次函数的表达式;
(2)直线与轴交于,现将线段上下移动,若线段与二次函数的图象有交点,求向上和向下平移的最大距离;
(3)若将(1)中二次函数图象平移,使其顶点与原点重合,然后将其图象绕点顺时针旋转,得到抛物线,如图2所示,直线与交于,两点,为上位于直线左侧一点,求面积最大值,及此时点的坐标.
15.如图,在平面直角坐标系中,抛物线与轴交于点,点,交轴于点.
(1)求抛物线的解析式;
(2)如图,连接,过点作射线交轴的正半轴于点,点与点关于原点对称,点是第四象限抛物线上一动点,过点作的垂线交于点,求线段长度的最大值及此时点的坐标;
(3)如图,把点向上平移个单位得到点,连接,把绕点顺时针旋转一定的角度,得到,其中边交坐标轴于点,在旋转过程中,是否存在一点,使得?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
五、作图题
16.已知二次函数
(1)完成下表:
(2)在下面的坐标系中描点,画出该二次函数的图象.
六、综合题
17.已知二次函数y=ax2的图象经过A(2,﹣4)
(1)求这个二次函数的解析式;
(2)请写出这个二次函数图象的顶点坐标、对称轴和开口方向.
18.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
19.如图,二次函数 的图象与y轴交于点C,点B在抛物线上,且点B与点C关于该二次函数图象的对称轴对称,已知一次函数 的图象经过该二次函数图象上点 及点B.
(1)求二次函数的解析式;
(2)根据图象,写出满足 的x的取值范围.
答案解析部分
1.【答案】x=1
【知识点】二次函数y=ax²+bx+c的性质
2.【答案】
【知识点】二次函数的最值
3.【答案】y=3(x﹣5)2
【知识点】二次函数图象的几何变换
4.【答案】16;-20
【知识点】二次函数的最值
5.【答案】<
【知识点】二次函数y=a(x-h)²+k的性质
6.【答案】(2,3)
【知识点】二次函数y=a(x-h)²+k的性质
7.【答案】D
【知识点】二次函数图象的几何变换
8.【答案】B
【知识点】二次函数图象的几何变换
9.【答案】D
【知识点】二次函数图象的几何变换
10.【答案】C
【知识点】二次函数图象的几何变换
11.【答案】D
【知识点】二次函数y=a(x-h)²+k的性质
12.【答案】
【知识点】待定系数法求二次函数解析式
13.【答案】解:∵抛物线过点(-1,0),(3,0),
∴,
解得:
∴a=1,b=-2.
【知识点】待定系数法求二次函数解析式
14.【答案】(1)
(2)CM向下平移的最大距离为,向上平移的最大距离为6.
(3)
【知识点】待定系数法求二次函数解析式;旋转的性质
15.【答案】(1)抛物线的解析式为;
(2),此时;
(3).
【知识点】待定系数法求二次函数解析式;解直角三角形;旋转的性质
16.【答案】(1)解:如下表,
x … -2 -1 0 1 2 3 4 …
y … -2 0 -2 …
(2)解:见下图,
【知识点】二次函数y=a(x-h)²+k的图象
17.【答案】(1)解:∵二次函数y=ax2的图象经过A(2,﹣4), ∴﹣4=4a,
解得a=﹣1,
∴二次函数的解析式为y=﹣x2
(2)解:∵二次函数的解析式为 y=﹣x2,
∴这个二次函数图象的顶点坐标为(0,0),对称轴为y轴,开口方向向下
【知识点】待定系数法求二次函数解析式;二次函数y=ax²的性质
18.【答案】(1)y=﹣20x2+100x+6000,0≤x<20(或0<x<20);(2)当降价2.5元时,利润最大且为6125元.
【知识点】二次函数的最值
19.【答案】(1)解: 抛物线 经过点 ,
,
,
抛物线解析式为 ;
(2)解:令 ,则 ,
点C坐标 ,
对称轴为直线 ,B、C关于对称轴对称,
点B坐标 ,
由图象可知,满足 的x的取值范围为 .
【知识点】待定系数法求二次函数解析式;二次函数y=a(x-h)²+k的性质
21世纪教育网(www.21cnjy.com)
7 / 7
