26章二次函数综合题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
26章二次函数综合题
一、填空题
1.抛物线 的对称轴是 .
2.若二次函数y=(m+1)x|m|的图象的开口向下,则m的值为 .
3.二次函数的顶点坐标为 .
4.将二次函数 化为 的形式为 .
5.已知二次函数的图象与坐标轴有三个公共点,则k的取值范围是 .
6.将抛物线绕原点旋转,则得到的抛物线的函数表达式为 .
二、单选题
7.将抛物线向右平移3个单位后得到新抛物线的顶点坐标为( )
A. B. C. D.
8.下列函数中,属于二次函数的是( )
A. B. C. D.
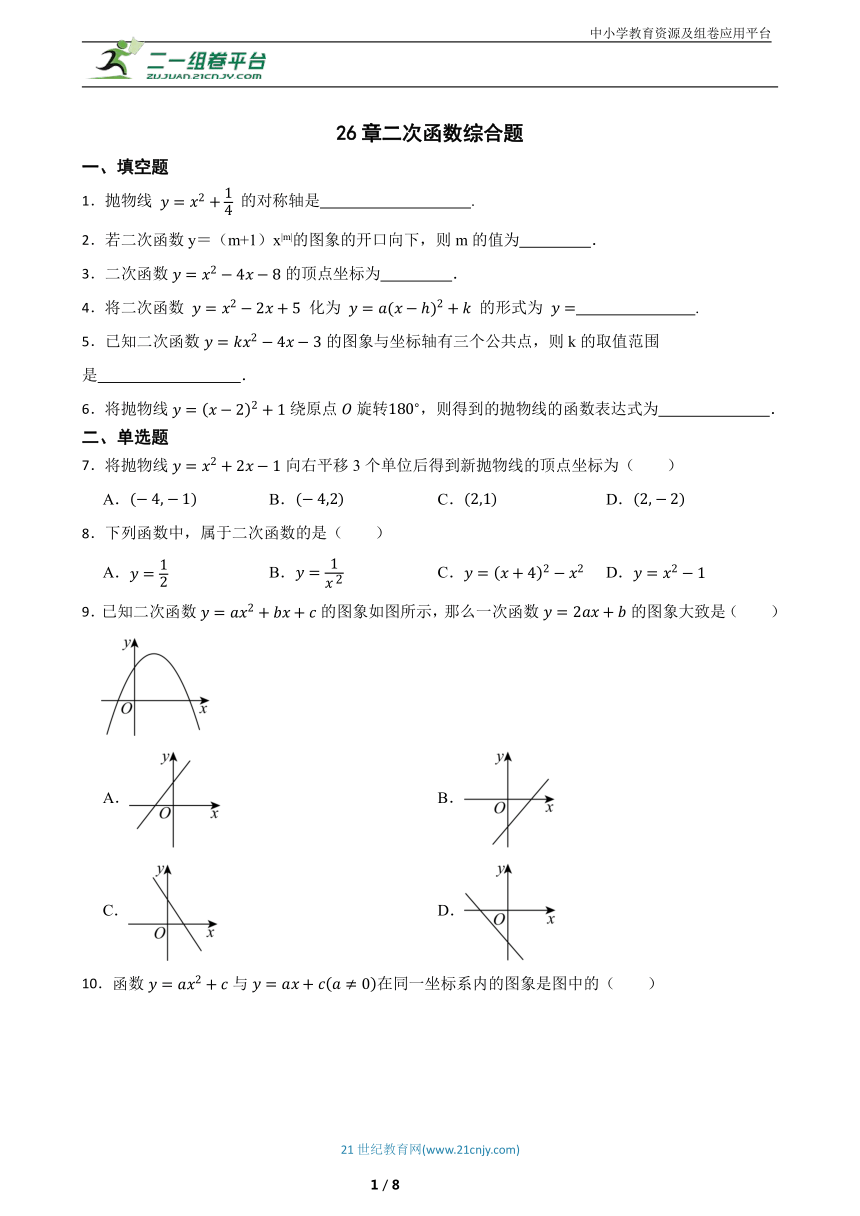
9.已知二次函数的图象如图所示,那么一次函数的图象大致是( )
A. B.
C. D.
10.函数与在同一坐标系内的图象是图中的( )
A. B.
C. D.
11.将二次函数的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
A. B. C. D.
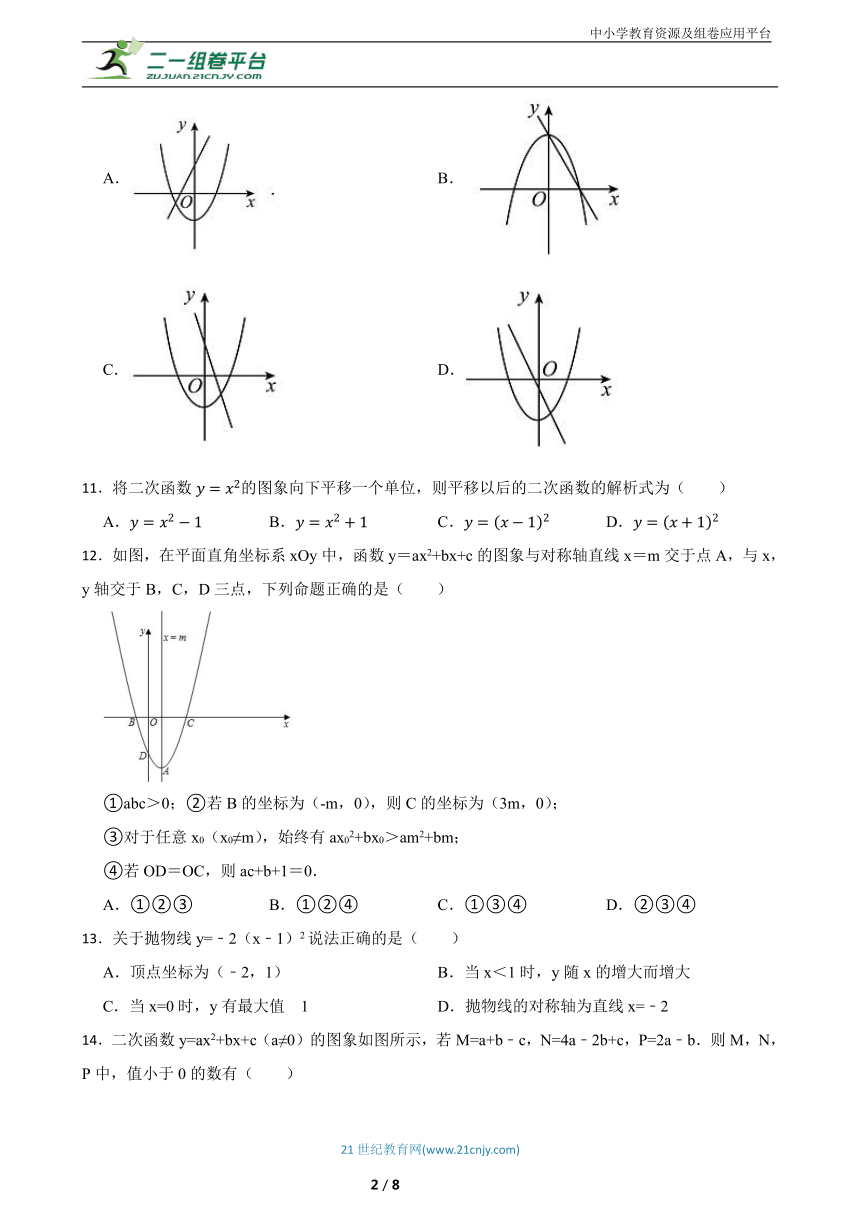
12.如图,在平面直角坐标系xOy中,函数y=ax2+bx+c的图象与对称轴直线x=m交于点A,与x,y轴交于B,C,D三点,下列命题正确的是( )
①abc>0;②若B的坐标为(-m,0),则C的坐标为(3m,0);
③对于任意x0(x0≠m),始终有ax02+bx0>am2+bm;
④若OD=OC,则ac+b+1=0.
A.①②③ B.①②④ C.①③④ D.②③④
13.关于抛物线y=﹣2(x﹣1)2说法正确的是( )
A.顶点坐标为(﹣2,1) B.当x<1时,y随x的增大而增大
C.当x=0时,y有最大值 1 D.抛物线的对称轴为直线x=﹣2
14.二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有( )
A.3个 B.2个 C.1个 D.0个
15.二次函数y = x2-2x-3的图象如图所示,则函数值y<0时,x的取值范围是( )
A.-1C.x>3 D.x<-1或 x>3
16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
A.1 B.2 C.3 D.4
三、解答题
17.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元;
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
18.图中是抛物线形拱桥,以为原点,水面所在直线为轴建立平面直角坐标系.如图1,点为桥拱的弧顶,在桥拱的点处安装一照明灯.
(1)求图1中桥拱所在抛物线的函数表达式.
(2)求的值.
(3)如图2,为方便船只通过,拱桥的桥拱需扩建,扩建后的桥拱所在抛物线与原桥拱所在抛物线的开口大小相同,照明灯安装在点处,求扩建后拱桥的桥拱跨度(即的长).
19.如图所示,在平面直角坐标系中,四边形为正方形,点A、C分别在x轴负半轴,y轴负半轴上,点,点B在第三象限内,点在函数的图像上
(1)求该反比例函数的解析式;
(2)连接,记的面积为S,设,求T的最大值.
20.如图,在平面直角坐标系中,是原点. 直线与轴、轴分别交于,两点,抛物线经过点,与轴的另一个交点为,与轴交于点.
(1)求这条抛物线的函数表达式.
(2)点是直线上的一个动点,设点的横坐标为,
①若的面积为,求关于的函数表达式;
②在直线上取,在的左侧,在直线的下方作正方形,求正方形与抛物线有两个交点时的取值范围.
四、计算题
21.有一条抛物线,三位学生分别说出了它的一些性质:
甲说:开口向下,对称轴是直线;
乙说:与轴的两个交点距离为6;
丙说:顶点在第一象限且与轴的交点围成的三角形面积等于9.
请你求出满足上述全部条件的一条抛物线的解析式.
22.用适当的方法解下列方程:
(1)2x2﹣8x=0.
(2)x2﹣3x+4=0.
(3)y= x2﹣x+3,求出抛物线的开口方向、对称轴、顶点坐标.
23.如图,一座温室实验室的横截面由抛物线和矩形组成,矩形的长是16m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,CD为一排平行于地面的加湿管.
(1)求抛物线的函数关系式,并计算出拱顶到地面的距离.
(2)若加湿管的长度至少是12m,加湿管与拱顶的距离至少是多少米?
(3)若在加湿管上方还要再安装一排恒温管(两排管道互相平行),且恒温管与加湿管相距1.25m,恒温管的长度至少是多少米?
答案解析部分
1.【答案】y轴(或 )
【知识点】二次函数y=a(x-h)²+k的图象
2.【答案】-2
【知识点】二次函数图象与系数的关系
3.【答案】
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
4.【答案】(x-1)2+4
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
5.【答案】且
【知识点】二次函数图象与坐标轴的交点问题
6.【答案】
【知识点】待定系数法求二次函数解析式;旋转的性质
7.【答案】D
【知识点】二次函数图象的几何变换
8.【答案】D
【知识点】二次函数的定义
9.【答案】C
【知识点】二次函数图象与系数的关系
10.【答案】B
【知识点】二次函数图象与系数的关系
11.【答案】A
【知识点】二次函数图象的几何变换
12.【答案】A
【知识点】二次函数图象与系数的关系;二次函数的最值;二次函数图象与坐标轴的交点问题
13.【答案】B
【知识点】二次函数y=a(x-h)²+k的图象;二次函数y=a(x-h)²+k的性质
14.【答案】A
【知识点】二次函数图象与系数的关系
15.【答案】A
【知识点】二次函数y=ax²+bx+c的图象
16.【答案】C
【知识点】二次函数图象与系数的关系
17.【答案】(1)y=1000-10x,w=-10x2+1300x-30000;(2)玩具销售单价为50元或80元时,可获得10000元销售利润.
【知识点】二次函数的实际应用-销售问题
18.【答案】(1)
(2)
(3)
【知识点】二次函数的实际应用-拱桥问题
19.【答案】(1)
(2)当时,有最大值,T的最大值是.
【知识点】待定系数法求反比例函数解析式;二次函数的最值;正方形的性质
20.【答案】(1)
(2)①②或
【知识点】待定系数法求二次函数解析式;解直角三角形
21.【答案】
【知识点】待定系数法求二次函数解析式
22.【答案】(1)解: 或
(2)解: ∴原方程无解.
(3)解: ∴抛物线开口向上,对称轴为直线 顶点坐标为
【知识点】公式法解一元二次方程;因式分解法解一元二次方程;二次函数y=a(x-h)²+k的性质;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
23.【答案】(1)y=-x2+x+4,拱顶到地面的距离为8米
(2)至少是2.25米
(3)至少是8米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
21世纪教育网(www.21cnjy.com)
2 / 8
26章二次函数综合题
一、填空题
1.抛物线 的对称轴是 .
2.若二次函数y=(m+1)x|m|的图象的开口向下,则m的值为 .
3.二次函数的顶点坐标为 .
4.将二次函数 化为 的形式为 .
5.已知二次函数的图象与坐标轴有三个公共点,则k的取值范围是 .
6.将抛物线绕原点旋转,则得到的抛物线的函数表达式为 .
二、单选题
7.将抛物线向右平移3个单位后得到新抛物线的顶点坐标为( )
A. B. C. D.
8.下列函数中,属于二次函数的是( )
A. B. C. D.
9.已知二次函数的图象如图所示,那么一次函数的图象大致是( )
A. B.
C. D.
10.函数与在同一坐标系内的图象是图中的( )
A. B.
C. D.
11.将二次函数的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
A. B. C. D.
12.如图,在平面直角坐标系xOy中,函数y=ax2+bx+c的图象与对称轴直线x=m交于点A,与x,y轴交于B,C,D三点,下列命题正确的是( )
①abc>0;②若B的坐标为(-m,0),则C的坐标为(3m,0);
③对于任意x0(x0≠m),始终有ax02+bx0>am2+bm;
④若OD=OC,则ac+b+1=0.
A.①②③ B.①②④ C.①③④ D.②③④
13.关于抛物线y=﹣2(x﹣1)2说法正确的是( )
A.顶点坐标为(﹣2,1) B.当x<1时,y随x的增大而增大
C.当x=0时,y有最大值 1 D.抛物线的对称轴为直线x=﹣2
14.二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有( )
A.3个 B.2个 C.1个 D.0个
15.二次函数y = x2-2x-3的图象如图所示,则函数值y<0时,x的取值范围是( )
A.-1
16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
A.1 B.2 C.3 D.4
三、解答题
17.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元;
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
18.图中是抛物线形拱桥,以为原点,水面所在直线为轴建立平面直角坐标系.如图1,点为桥拱的弧顶,在桥拱的点处安装一照明灯.
(1)求图1中桥拱所在抛物线的函数表达式.
(2)求的值.
(3)如图2,为方便船只通过,拱桥的桥拱需扩建,扩建后的桥拱所在抛物线与原桥拱所在抛物线的开口大小相同,照明灯安装在点处,求扩建后拱桥的桥拱跨度(即的长).
19.如图所示,在平面直角坐标系中,四边形为正方形,点A、C分别在x轴负半轴,y轴负半轴上,点,点B在第三象限内,点在函数的图像上
(1)求该反比例函数的解析式;
(2)连接,记的面积为S,设,求T的最大值.
20.如图,在平面直角坐标系中,是原点. 直线与轴、轴分别交于,两点,抛物线经过点,与轴的另一个交点为,与轴交于点.
(1)求这条抛物线的函数表达式.
(2)点是直线上的一个动点,设点的横坐标为,
①若的面积为,求关于的函数表达式;
②在直线上取,在的左侧,在直线的下方作正方形,求正方形与抛物线有两个交点时的取值范围.
四、计算题
21.有一条抛物线,三位学生分别说出了它的一些性质:
甲说:开口向下,对称轴是直线;
乙说:与轴的两个交点距离为6;
丙说:顶点在第一象限且与轴的交点围成的三角形面积等于9.
请你求出满足上述全部条件的一条抛物线的解析式.
22.用适当的方法解下列方程:
(1)2x2﹣8x=0.
(2)x2﹣3x+4=0.
(3)y= x2﹣x+3,求出抛物线的开口方向、对称轴、顶点坐标.
23.如图,一座温室实验室的横截面由抛物线和矩形组成,矩形的长是16m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,CD为一排平行于地面的加湿管.
(1)求抛物线的函数关系式,并计算出拱顶到地面的距离.
(2)若加湿管的长度至少是12m,加湿管与拱顶的距离至少是多少米?
(3)若在加湿管上方还要再安装一排恒温管(两排管道互相平行),且恒温管与加湿管相距1.25m,恒温管的长度至少是多少米?
答案解析部分
1.【答案】y轴(或 )
【知识点】二次函数y=a(x-h)²+k的图象
2.【答案】-2
【知识点】二次函数图象与系数的关系
3.【答案】
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
4.【答案】(x-1)2+4
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
5.【答案】且
【知识点】二次函数图象与坐标轴的交点问题
6.【答案】
【知识点】待定系数法求二次函数解析式;旋转的性质
7.【答案】D
【知识点】二次函数图象的几何变换
8.【答案】D
【知识点】二次函数的定义
9.【答案】C
【知识点】二次函数图象与系数的关系
10.【答案】B
【知识点】二次函数图象与系数的关系
11.【答案】A
【知识点】二次函数图象的几何变换
12.【答案】A
【知识点】二次函数图象与系数的关系;二次函数的最值;二次函数图象与坐标轴的交点问题
13.【答案】B
【知识点】二次函数y=a(x-h)²+k的图象;二次函数y=a(x-h)²+k的性质
14.【答案】A
【知识点】二次函数图象与系数的关系
15.【答案】A
【知识点】二次函数y=ax²+bx+c的图象
16.【答案】C
【知识点】二次函数图象与系数的关系
17.【答案】(1)y=1000-10x,w=-10x2+1300x-30000;(2)玩具销售单价为50元或80元时,可获得10000元销售利润.
【知识点】二次函数的实际应用-销售问题
18.【答案】(1)
(2)
(3)
【知识点】二次函数的实际应用-拱桥问题
19.【答案】(1)
(2)当时,有最大值,T的最大值是.
【知识点】待定系数法求反比例函数解析式;二次函数的最值;正方形的性质
20.【答案】(1)
(2)①②或
【知识点】待定系数法求二次函数解析式;解直角三角形
21.【答案】
【知识点】待定系数法求二次函数解析式
22.【答案】(1)解: 或
(2)解: ∴原方程无解.
(3)解: ∴抛物线开口向上,对称轴为直线 顶点坐标为
【知识点】公式法解一元二次方程;因式分解法解一元二次方程;二次函数y=a(x-h)²+k的性质;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
23.【答案】(1)y=-x2+x+4,拱顶到地面的距离为8米
(2)至少是2.25米
(3)至少是8米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
21世纪教育网(www.21cnjy.com)
2 / 8
