27.1圆的认识本节综合题(含答案)
文档属性
| 名称 | 27.1圆的认识本节综合题(含答案) |

|
|
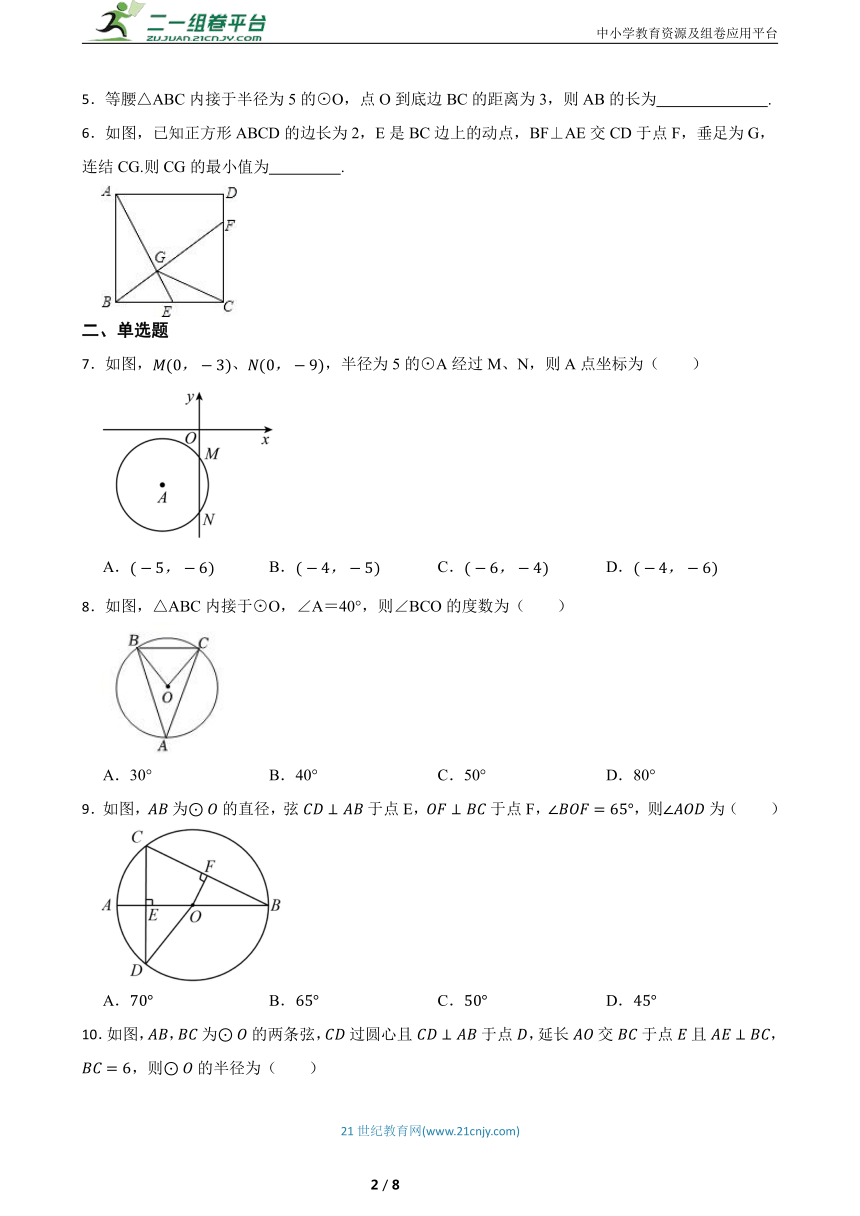
| 格式 | docx | ||
| 文件大小 | 404.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 14:28:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
27.1圆的认识本节综合题
一、填空题
1.如图,在 中, ,则 度.
2.如图所示,在中,直径,弦于点C,连接.若,则的长为 .
3.如图,半圆的直径,将半圆绕点B顺时针旋转45°得到半圆,与AB交于点P,那么AP的长为 .
4.如图,已知的半径为7,是的弦,点P在弦上.若,,则的长为 .
5.等腰△ABC内接于半径为5的⊙O,点O到底边BC的距离为3,则AB的长为 .
6.如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为 .
二、单选题
7.如图,、,半径为5的⊙A经过M、N,则A点坐标为( )
A. B. C. D.
8.如图,△ABC内接于⊙O,∠A=40°,则∠BCO的度数为( )
A.30° B.40° C.50° D.80°
9.如图,为的直径,弦于点E,于点F,,则为( )
A. B. C. D.
10.如图,,为的两条弦,过圆心且于点,延长交于点且,,则的半径为( )
A.7 B. C. D.
11.下列图形中的角是圆周角的是( )
A. B. C. D.
12.如图, 是 的直径, ,则 的度数为( )
A. B. C. D.
13.如图,AB是⊙O的直径,C、D是圆上的点,若∠D=20°,则 ∠BAC的值( )
A.20° B.60° C.70° D.80°
14.下列结论正确的是( )
A. 经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与直径相交的直线是圆的对称轴
15.已知AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是( )
A.3 B.4 C.5 D.6
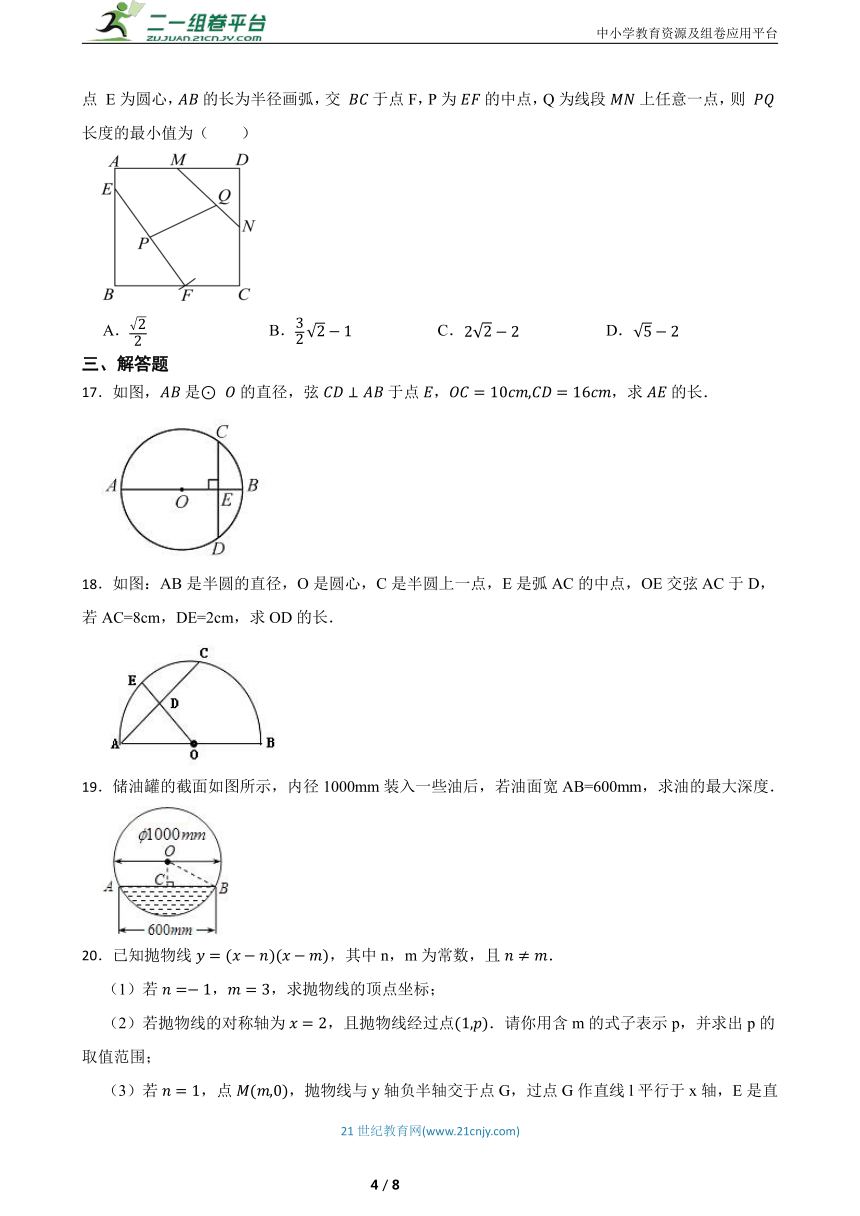
16.如图,在正方形中,,M,N分别为边 , 的中点,E为边上一动点,以点 E为圆心,的长为半径画弧,交 于点F,P为的中点,Q为线段上任意一点,则 长度的最小值为( )
A. B. C. D.
三、解答题
17.如图,是的直径,弦于点,,求的长.
18.如图:AB是半圆的直径,O是圆心,C是半圆上一点,E是弧AC的中点,OE交弦AC于D,若AC=8cm,DE=2cm,求OD的长.
19.储油罐的截面如图所示,内径1000mm装入一些油后,若油面宽AB=600mm,求油的最大深度.
20.已知抛物线,其中n,m为常数,且.
(1)若,,求抛物线的顶点坐标;
(2)若抛物线的对称轴为,且抛物线经过点.请你用含m的式子表示p,并求出p的取值范围;
(3)若,点,抛物线与y轴负半轴交于点G,过点G作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点,,点H是的中点,当的最小值是时,求在的图象的最低点的坐标.
四、计算题
21.(1)解方程:
(2)如图,惠州滨江公园有一石拱桥是圆弧形(劣弧),O为拱桥所在圆弧形的圆心.其跨度米,拱高为8米,求圆弧所在的圆的半径.
22.如图,已知在中,,,点G是的重心,延长交边于点D,以G为圆心,为半径的圆分别交边、于点E、F.
(1)求的长;
(2)求的长.
23.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
答案解析部分
1.【答案】80
【知识点】圆周角定理
2.【答案】
【知识点】勾股定理;垂径定理
3.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;圆周角定理;旋转的性质
4.【答案】5
【知识点】勾股定理;垂径定理
5.【答案】2 或4
【知识点】勾股定理;垂径定理
6.【答案】 ﹣1
【知识点】正方形的性质;圆周角定理
7.【答案】D
【知识点】坐标与图形性质;勾股定理;垂径定理
8.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
9.【答案】C
【知识点】圆周角定理;邻补角
10.【答案】C
【知识点】垂径定理;解直角三角形
11.【答案】A
【知识点】圆周角定理
12.【答案】C
【知识点】圆周角定理
13.【答案】C
【知识点】圆周角定理
14.【答案】A
【知识点】圆的相关概念
15.【答案】D
【知识点】垂径定理
16.【答案】B
【知识点】勾股定理;正方形的性质;圆的相关概念;直角三角形斜边上的中线
17.【答案】
【知识点】勾股定理;垂径定理
18.【答案】3cm
【知识点】垂径定理
19.【答案】解:延长OC交⊙O于点D,
∵OC⊥AB于点C,
∴BC= AB= ×600=300mm,
∵⊙O的直径为1000mm
∴OB=500mm
∵在Rt△OCB中,OC= = =400mm,
∴DC=OD﹣OC=500﹣400=100(mm).
答:油的最大深度为100mm
【知识点】勾股定理;垂径定理的实际应用
20.【答案】(1)
(2),
(3)或
【知识点】勾股定理;圆的相关概念;直角三角形斜边上的中线
21.【答案】(1),
(2)13米
【知识点】因式分解法解一元二次方程;勾股定理;垂径定理的实际应用
22.【答案】(1)
(2)
【知识点】勾股定理;垂径定理;解直角三角形;三角形的重心及应用
23.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
21世纪教育网(www.21cnjy.com)
8 / 8
27.1圆的认识本节综合题
一、填空题
1.如图,在 中, ,则 度.
2.如图所示,在中,直径,弦于点C,连接.若,则的长为 .
3.如图,半圆的直径,将半圆绕点B顺时针旋转45°得到半圆,与AB交于点P,那么AP的长为 .
4.如图,已知的半径为7,是的弦,点P在弦上.若,,则的长为 .
5.等腰△ABC内接于半径为5的⊙O,点O到底边BC的距离为3,则AB的长为 .
6.如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为 .
二、单选题
7.如图,、,半径为5的⊙A经过M、N,则A点坐标为( )
A. B. C. D.
8.如图,△ABC内接于⊙O,∠A=40°,则∠BCO的度数为( )
A.30° B.40° C.50° D.80°
9.如图,为的直径,弦于点E,于点F,,则为( )
A. B. C. D.
10.如图,,为的两条弦,过圆心且于点,延长交于点且,,则的半径为( )
A.7 B. C. D.
11.下列图形中的角是圆周角的是( )
A. B. C. D.
12.如图, 是 的直径, ,则 的度数为( )
A. B. C. D.
13.如图,AB是⊙O的直径,C、D是圆上的点,若∠D=20°,则 ∠BAC的值( )
A.20° B.60° C.70° D.80°
14.下列结论正确的是( )
A. 经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与直径相交的直线是圆的对称轴
15.已知AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是( )
A.3 B.4 C.5 D.6
16.如图,在正方形中,,M,N分别为边 , 的中点,E为边上一动点,以点 E为圆心,的长为半径画弧,交 于点F,P为的中点,Q为线段上任意一点,则 长度的最小值为( )
A. B. C. D.
三、解答题
17.如图,是的直径,弦于点,,求的长.
18.如图:AB是半圆的直径,O是圆心,C是半圆上一点,E是弧AC的中点,OE交弦AC于D,若AC=8cm,DE=2cm,求OD的长.
19.储油罐的截面如图所示,内径1000mm装入一些油后,若油面宽AB=600mm,求油的最大深度.
20.已知抛物线,其中n,m为常数,且.
(1)若,,求抛物线的顶点坐标;
(2)若抛物线的对称轴为,且抛物线经过点.请你用含m的式子表示p,并求出p的取值范围;
(3)若,点,抛物线与y轴负半轴交于点G,过点G作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点,,点H是的中点,当的最小值是时,求在的图象的最低点的坐标.
四、计算题
21.(1)解方程:
(2)如图,惠州滨江公园有一石拱桥是圆弧形(劣弧),O为拱桥所在圆弧形的圆心.其跨度米,拱高为8米,求圆弧所在的圆的半径.
22.如图,已知在中,,,点G是的重心,延长交边于点D,以G为圆心,为半径的圆分别交边、于点E、F.
(1)求的长;
(2)求的长.
23.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
答案解析部分
1.【答案】80
【知识点】圆周角定理
2.【答案】
【知识点】勾股定理;垂径定理
3.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;圆周角定理;旋转的性质
4.【答案】5
【知识点】勾股定理;垂径定理
5.【答案】2 或4
【知识点】勾股定理;垂径定理
6.【答案】 ﹣1
【知识点】正方形的性质;圆周角定理
7.【答案】D
【知识点】坐标与图形性质;勾股定理;垂径定理
8.【答案】C
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理
9.【答案】C
【知识点】圆周角定理;邻补角
10.【答案】C
【知识点】垂径定理;解直角三角形
11.【答案】A
【知识点】圆周角定理
12.【答案】C
【知识点】圆周角定理
13.【答案】C
【知识点】圆周角定理
14.【答案】A
【知识点】圆的相关概念
15.【答案】D
【知识点】垂径定理
16.【答案】B
【知识点】勾股定理;正方形的性质;圆的相关概念;直角三角形斜边上的中线
17.【答案】
【知识点】勾股定理;垂径定理
18.【答案】3cm
【知识点】垂径定理
19.【答案】解:延长OC交⊙O于点D,
∵OC⊥AB于点C,
∴BC= AB= ×600=300mm,
∵⊙O的直径为1000mm
∴OB=500mm
∵在Rt△OCB中,OC= = =400mm,
∴DC=OD﹣OC=500﹣400=100(mm).
答:油的最大深度为100mm
【知识点】勾股定理;垂径定理的实际应用
20.【答案】(1)
(2),
(3)或
【知识点】勾股定理;圆的相关概念;直角三角形斜边上的中线
21.【答案】(1),
(2)13米
【知识点】因式分解法解一元二次方程;勾股定理;垂径定理的实际应用
22.【答案】(1)
(2)
【知识点】勾股定理;垂径定理;解直角三角形;三角形的重心及应用
23.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
21世纪教育网(www.21cnjy.com)
8 / 8
