27.2.2直线与圆的位置关系 同步练习(含答案)
文档属性
| 名称 | 27.2.2直线与圆的位置关系 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.2.2直线与圆的位置关系
一、填空题
1.已知的半径为,圆心到直线的距离为,则直线与的位置关系是 .
2.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .
3.已知的半径为,点到直线的距离为.把直线向上平移 ,才能使与相切
4.设的半径为,点在直线上,已知,那么直线与的位置关系是 .
5.如图,直线与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P坐标为 .
6.如图,在中,,,,D是上一动点,于E,交于点F,则取最大值时,的值为 .
二、单选题
7.已知⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,那么直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
8.已知的半径是,点到直线的距离为,则直线与的位置关系是( )
A.相离 B.相交 C.相切 D.无法判断
9.已知平面内有 和点 , 若 的半径为 , 线段 , 则直线 与 的位置关系为( )
A.相离 B.相交 C.相切 D.相交或相切
10.如图,若的半径为6,圆心O到一条直线的距离为3,则这条直线可能是( )
A. B. C. D.
11.⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.内含
12. 的圆心到直线a的距离为3cm, 的半径为 ,将直线a向垂直于a的方向平移,使a与 相切,则平移的距离是( )
A. B. C. D. 或
13.如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y= (x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2 时,点P的坐标为( )
A.(1,6)和(6,1)
B.(2,3)和(3,2)
C.( ,3 )和(3 , )
D.( ,2 )和(2 , )
14.如图,已知⊙ 的半径为3,圆外一点 满足 ,点 为⊙ 上一动点,经过点 的直线 上有两点 、 ,且OA=OB,∠APB=90°, 不经过点 ,则 的最小值( )
A.2 B.4 C.5 D.6
三、解答题
15.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
16.如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,=,FB=1,求⊙O的半径.
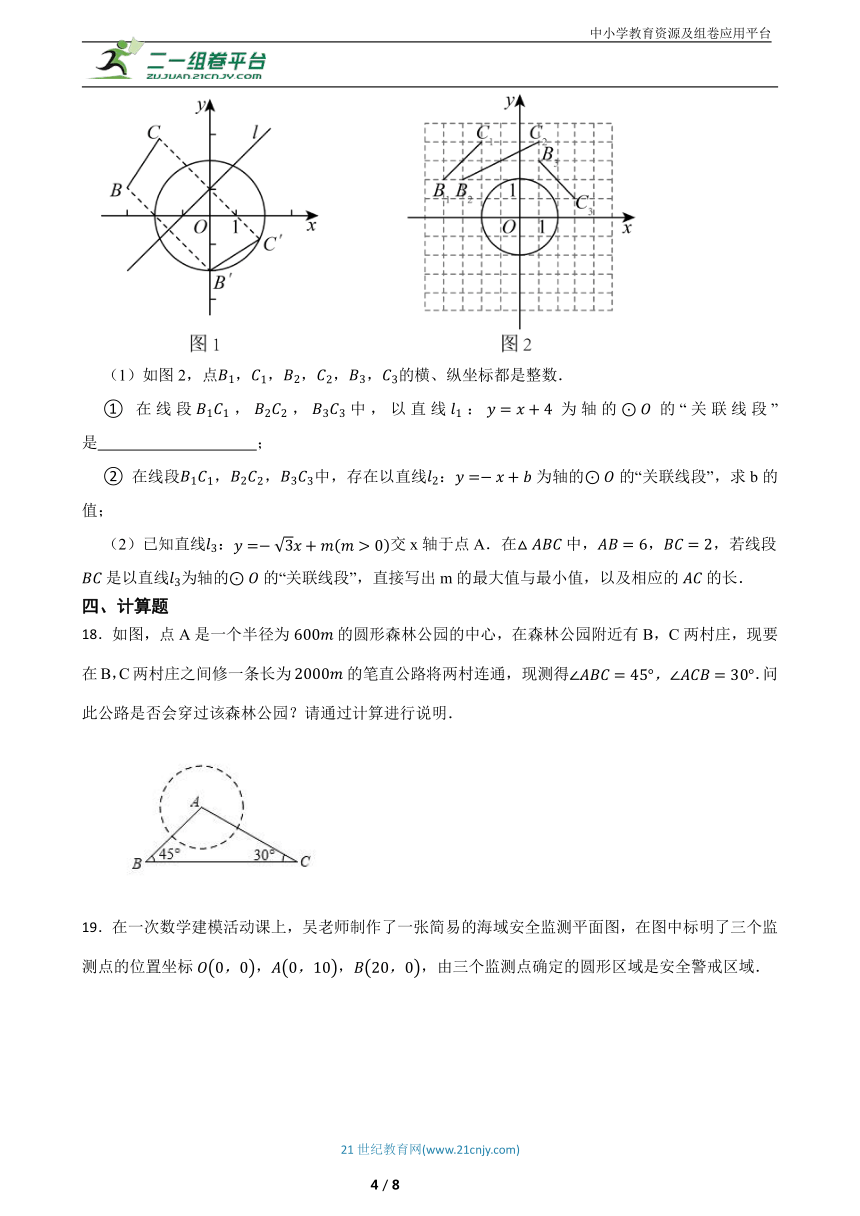
17.在平面直角坐标系中,的半径为2.对于直线l和线段,给出如下定义:若将线段关于直线l对称,可以得到的弦 (,分别是B,C的对应点),则称线段是以直线l为轴的的“关联线段”.例如,图1中线段是以直线l为轴的的“关联线段”.
(1)如图2,点,,,,,的横、纵坐标都是整数.
① 在线段,,中,以直线:为轴的的“关联线段”是 ;
② 在线段,,中,存在以直线:为轴的的“关联线段”,求b的值;
(2)已知直线:交x轴于点A.在中,,,若线段是以直线为轴的的“关联线段”,直接写出m的最大值与最小值,以及相应的的长.
四、计算题
18.如图,点A是一个半径为的圆形森林公园的中心,在森林公园附近有B,C两村庄,现要在B,C两村庄之间修一条长为的笔直公路将两村连通, 现测得.问此公路是否会穿过该森林公园?请通过计算进行说明.
19.在一次数学建模活动课上,吴老师制作了一张简易的海域安全监测平面图,在图中标明了三个监测点的位置坐标,,,由三个监测点确定的圆形区域是安全警戒区域.
(1)某天海面上出现可疑船只C,在监测点A测得C位于南偏东,同时在监测点O测得C位于南偏东,求监测点O到C船的距离.(结果精确到,参考数据:,,,)
(2)当可疑船只C由(1)中位置向正北方向航行时,是否会闯入安全警戒区域?请通过计算作答.
答案解析部分
1.【答案】相交
【知识点】直线与圆的位置关系
2.【答案】相离
【知识点】直线与圆的位置关系
3.【答案】或
【知识点】直线与圆的位置关系
4.【答案】相切或相交
【知识点】直线与圆的位置关系
5.【答案】(-2,0)、(-3,0)、(-4,0)
【知识点】直线与圆的位置关系;圆-动点问题
6.【答案】
【知识点】直线与圆的位置关系;解直角三角形
7.【答案】A
【知识点】直线与圆的位置关系
8.【答案】B
【知识点】直线与圆的位置关系
9.【答案】D
【知识点】点与圆的位置关系;直线与圆的位置关系
10.【答案】B
【知识点】直线与圆的位置关系
11.【答案】C
【知识点】直线与圆的位置关系
12.【答案】D
【知识点】直线与圆的位置关系
13.【答案】C
【知识点】反比例函数与一次函数的交点问题;直线与圆的位置关系
14.【答案】B
【知识点】等腰三角形的性质;直线与圆的位置关系
15.【答案】相切
【知识点】直线与圆的位置关系
16.【答案】(1)如图,连接OG.
∵OA=OG,∴∠OGA=∠OAG.
∵CD⊥AB,∴∠AKH+∠OAG=90°.
∵KE=GE,
∴∠KGE=∠GKE=∠AKH.
∴∠KGE+∠OGA=∠AKH+∠OAG=90°.
∴∠OGE=90°,即OG⊥EF.
又∵G在圆O上,∴EF与圆O相切.
(2)∵AC∥EF, ∴∠F=∠CAH,
∴Rt△AHC∽ Rt△FGO. ∴.
∵在Rt△OAH中,,设AH=3t,则AC=5t,CH=4t.
∴. ∴.
∵FB=1∴,解得:OG=4.
∴圆O的半径为4 .
【知识点】直线与圆的位置关系
17.【答案】(1)①;② 1或3
(2)m的最大值为,;m的最小值为,.
【知识点】直线与圆的位置关系;轴对称的性质
18.【答案】此公路不会穿过该森林公园
【知识点】直线与圆的位置关系;解直角三角形的其他实际应用
19.【答案】(1)
(2)不会
【知识点】矩形的判定与性质;直线与圆的位置关系;相似三角形的判定与性质;解直角三角形的实际应用﹣方向角问题
21世纪教育网(www.21cnjy.com)
5 / 8
27.2.2直线与圆的位置关系
一、填空题
1.已知的半径为,圆心到直线的距离为,则直线与的位置关系是 .
2.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .
3.已知的半径为,点到直线的距离为.把直线向上平移 ,才能使与相切
4.设的半径为,点在直线上,已知,那么直线与的位置关系是 .
5.如图,直线与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P坐标为 .
6.如图,在中,,,,D是上一动点,于E,交于点F,则取最大值时,的值为 .
二、单选题
7.已知⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,那么直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
8.已知的半径是,点到直线的距离为,则直线与的位置关系是( )
A.相离 B.相交 C.相切 D.无法判断
9.已知平面内有 和点 , 若 的半径为 , 线段 , 则直线 与 的位置关系为( )
A.相离 B.相交 C.相切 D.相交或相切
10.如图,若的半径为6,圆心O到一条直线的距离为3,则这条直线可能是( )
A. B. C. D.
11.⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.内含
12. 的圆心到直线a的距离为3cm, 的半径为 ,将直线a向垂直于a的方向平移,使a与 相切,则平移的距离是( )
A. B. C. D. 或
13.如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y= (x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2 时,点P的坐标为( )
A.(1,6)和(6,1)
B.(2,3)和(3,2)
C.( ,3 )和(3 , )
D.( ,2 )和(2 , )
14.如图,已知⊙ 的半径为3,圆外一点 满足 ,点 为⊙ 上一动点,经过点 的直线 上有两点 、 ,且OA=OB,∠APB=90°, 不经过点 ,则 的最小值( )
A.2 B.4 C.5 D.6
三、解答题
15.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,试判断半径为3的圆与OA的位置关系.
16.如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,=,FB=1,求⊙O的半径.
17.在平面直角坐标系中,的半径为2.对于直线l和线段,给出如下定义:若将线段关于直线l对称,可以得到的弦 (,分别是B,C的对应点),则称线段是以直线l为轴的的“关联线段”.例如,图1中线段是以直线l为轴的的“关联线段”.
(1)如图2,点,,,,,的横、纵坐标都是整数.
① 在线段,,中,以直线:为轴的的“关联线段”是 ;
② 在线段,,中,存在以直线:为轴的的“关联线段”,求b的值;
(2)已知直线:交x轴于点A.在中,,,若线段是以直线为轴的的“关联线段”,直接写出m的最大值与最小值,以及相应的的长.
四、计算题
18.如图,点A是一个半径为的圆形森林公园的中心,在森林公园附近有B,C两村庄,现要在B,C两村庄之间修一条长为的笔直公路将两村连通, 现测得.问此公路是否会穿过该森林公园?请通过计算进行说明.
19.在一次数学建模活动课上,吴老师制作了一张简易的海域安全监测平面图,在图中标明了三个监测点的位置坐标,,,由三个监测点确定的圆形区域是安全警戒区域.
(1)某天海面上出现可疑船只C,在监测点A测得C位于南偏东,同时在监测点O测得C位于南偏东,求监测点O到C船的距离.(结果精确到,参考数据:,,,)
(2)当可疑船只C由(1)中位置向正北方向航行时,是否会闯入安全警戒区域?请通过计算作答.
答案解析部分
1.【答案】相交
【知识点】直线与圆的位置关系
2.【答案】相离
【知识点】直线与圆的位置关系
3.【答案】或
【知识点】直线与圆的位置关系
4.【答案】相切或相交
【知识点】直线与圆的位置关系
5.【答案】(-2,0)、(-3,0)、(-4,0)
【知识点】直线与圆的位置关系;圆-动点问题
6.【答案】
【知识点】直线与圆的位置关系;解直角三角形
7.【答案】A
【知识点】直线与圆的位置关系
8.【答案】B
【知识点】直线与圆的位置关系
9.【答案】D
【知识点】点与圆的位置关系;直线与圆的位置关系
10.【答案】B
【知识点】直线与圆的位置关系
11.【答案】C
【知识点】直线与圆的位置关系
12.【答案】D
【知识点】直线与圆的位置关系
13.【答案】C
【知识点】反比例函数与一次函数的交点问题;直线与圆的位置关系
14.【答案】B
【知识点】等腰三角形的性质;直线与圆的位置关系
15.【答案】相切
【知识点】直线与圆的位置关系
16.【答案】(1)如图,连接OG.
∵OA=OG,∴∠OGA=∠OAG.
∵CD⊥AB,∴∠AKH+∠OAG=90°.
∵KE=GE,
∴∠KGE=∠GKE=∠AKH.
∴∠KGE+∠OGA=∠AKH+∠OAG=90°.
∴∠OGE=90°,即OG⊥EF.
又∵G在圆O上,∴EF与圆O相切.
(2)∵AC∥EF, ∴∠F=∠CAH,
∴Rt△AHC∽ Rt△FGO. ∴.
∵在Rt△OAH中,,设AH=3t,则AC=5t,CH=4t.
∴. ∴.
∵FB=1∴,解得:OG=4.
∴圆O的半径为4 .
【知识点】直线与圆的位置关系
17.【答案】(1)①;② 1或3
(2)m的最大值为,;m的最小值为,.
【知识点】直线与圆的位置关系;轴对称的性质
18.【答案】此公路不会穿过该森林公园
【知识点】直线与圆的位置关系;解直角三角形的其他实际应用
19.【答案】(1)
(2)不会
【知识点】矩形的判定与性质;直线与圆的位置关系;相似三角形的判定与性质;解直角三角形的实际应用﹣方向角问题
21世纪教育网(www.21cnjy.com)
5 / 8
