2025届中考数学一轮复习备考 专题二 代数式与整式 课件(共60张PPT)
文档属性
| 名称 | 2025届中考数学一轮复习备考 专题二 代数式与整式 课件(共60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-30 16:16:26 | ||
图片预览











文档简介
(共60张PPT)
专题二 代数式与整式
中考数学一轮复习备考合集
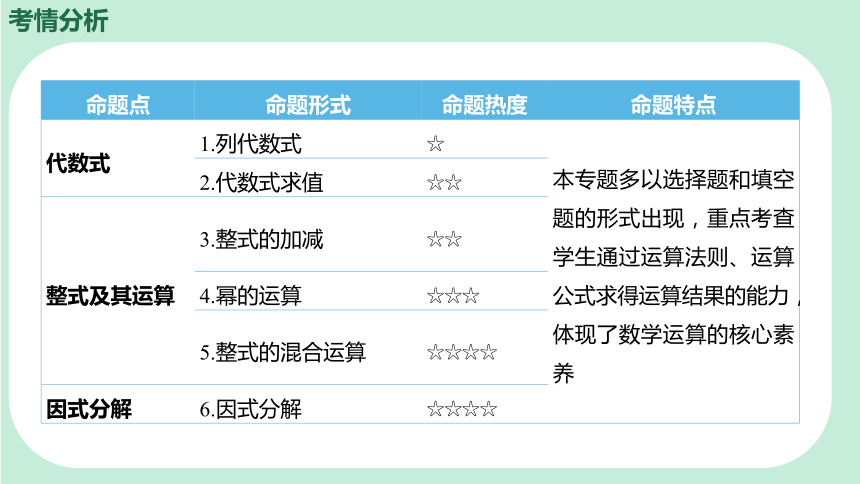
考情分析
命题点 命题形式 命题热度 命题特点
代数式 1.列代数式 ☆ 本专题多以选择题和填空题的形式出现,重点考查学生通过运算法则、运算公式求得运算结果的能力,体现了数学运算的核心素养
2.代数式求值 ☆☆ 整式及其运算 3.整式的加减 ☆☆ 4.幂的运算 ☆☆☆ 5.整式的混合运算 ☆☆☆☆ 因式分解 6.因式分解 ☆☆☆☆
讲解一:
代数式及其分类
知识复习
一、用字母表示数
1.用字母或含有字母的式子表示数或数量关系.在用字母表示数中,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
知识复习
一、用字母表示数
2.用含有字母的式子表示数的书写规定
(2)数与字母相乘时,通常把数写在前面;
(4)带分数与字母相乘时要将带分数化为假分数;
(5)除法运算要表示成分数;
(6)若式子后面有单位且式子是和或差的形式,式子应用小括号括起来.
知识复习
一、用字母表示数
【注意】
1.同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示;
2.用字母可以表示任意数或式子.用字母表示数后,同一式子可以表示不同的含义;
3.用字母表示实际问题中的某个量时,字母的取值必须使式子有意义且符合实际情况.
知识复习
二、代数式的定义
1.单独的一个数或一个字母也是代数式.
用基本运算符号把数和表示数的字母连接起来的式子.
【注意】
知识复习
三、列代数式的要点
通过题目中的关键词(如和、差、积、商、大、小、几倍、几分之几等),找到正确的数量关系.常见数量关系如下:
知识复习
四、代数式求值的常用方法
1.直接代入法:已知字母的值或字母的值可计算时,直接代入求解.
2.整体代入法:字母的值不能或不必计算时,先对已知或所求代数式进行变形(常用到提取公因式、平方差公式、完全平方公式等),再整体代入求解.
命题形式1 列代数式
B
命题形式2 代数式求值
11
命题形式2代数式求值
4
讲解二:
整式的相关概念
知识复习
一、单项式:
类别 定义 示例
系数 单项式中的数字因数
次数 单项式中的所有字母的指数和 单项式的相关概念如下:
知识复习
一、单项式:
1.乘积:只含乘法,不含加法
2.单独的一个数或字母也是单项式
3.分母中不能含有字母
4.若单项式只含有字母因数,则它的系数就是1或-1
5.对于单独一个非零的数,规定它的次数为0
6.π是常数而不是字母
知识复习
二、多项式
类别 定义 示例
项 组成多项式的每个单项式
项数 组成多项式的单项式的个数 次数 多项式中次数最高项的次数 多项式的相关概念如下:
知识复习
多项式
1.不含字母的项叫做常数项
2.多项式的每一项都包括它前面的符号
4.单项式与多项式统称为整式
命题形式3 单项式的有关内容
3
4
命题形式3 单项式的有关内容
【题型解读】
此题考查单项式有关概念,根据单项式次数的定义来求解,解题的关键是需灵活掌握单项式的系数和次数的定义,单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
命题形式4 多项式的有关内容
五
四
讲解三:
整式的加减
知识复习
一、合并同类项
1.同类项:所含字母相同,且相同字母的指数也相同的项
2.同类项与单项式的系数无关,与字母的顺序无关.
3.常数项都是同类项
4.若多个同类项的系数相加为0,则合并后该项为0
将同类项的系数相加,字母与其指数不变
知识复习
二、去括号法则
符号 法则 举例
括号前是 “+” 去、添括号不变号
括号前是“-” 去、添括号都变号
添括号与去括号的过程相反,添括号是否正确,可用去括号检验.
知识复习
三、整式的加减
整式的加减的实质是合并同类项,如果有括号要先去括号,再合并同类项.
命题形式5 整式的加减
A
【题型解读】
本题主要考查合并同类项,根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变即可得.
命题形式5 整式的加减
讲解四:
幂的运算
知识复习
幂的运算
类别 运算法则 运算公式 逆用
同底数幂的乘法
幂的乘方
积的乘方
底数不变,指数相加
底数不变,指数相乘
把积的每一个因式分别乘方,再把所得的幂相乘
知识复习
类别 运算法则 运算公式 逆用
同底数幂的除法
零次幂
负指数幂
底数不变,指数相减
任何非零数的0次幂都等于1
指数转正,再取倒数
幂的运算
命题形式6 幂的运算
D
命题形式6 幂的运算
B
命题形式6 幂的运算
【题型解读】
该题型考查合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键.根据合并同类项法则;同底数幂相乘,底数不变,指数相加;幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减,对各选项分析判断后利用排除法求解.
讲解五:
整式的乘除
知识复习
一、整式的乘法
类别 运算法则 示例
单项式×单项式
单项式×多项式
多项式×多项式
①系数相乘;
②同底数幂相乘;
③单独含有的字母连同指数不变
①单项式乘多项式的每一项;
②积相加
①将多项式的每一项分别相乘
②积相加
知识复习
二、整式的除法
类别 运算法则 举例
单项式÷单项式
多项式÷单项式
①系数相除;
②同底数幂相除;
③只在被除式里含有的字母连同指数不变
①用多项式的每一项除以单项式
②商相加
D
命题形式7 整式的混合运算
【题型解读】
本题主要考查了整式的混合运算,先计算单项式乘以多项式,再合并同类项即可.
C
命题形式7 整式的混合运算
命题形式7 整式的混合运算
【题型解读】
本题考查了合并同类项,积的乘方,单项式除以单项式,单项式乘以单项式,根据合并同类项,积的乘方,单项式除以单项式,单项式乘以单项式法则逐项排除即可,熟练掌握运算法则是解题的关键.
命题形式7 整式的混合运算
讲解六:
乘法公式
知识复习
一、平方差公式:
知识复习
一、平方差公式:
1.位置:
2.系数:
3.指数:
4.项数:
知识复习
二、完全平方公式:
完全平方公式 和的完全平方公式
差的完全平方公式
知识复习
三、【难点突破】
在用完全平方公式对代数式变形时,常用到下列关系:
命题形式8 利用乘法公式解题
命题形式8 利用乘法公式解题
【题型解读】
根据单项式乘以多项式和完全平方公式法则分别计算,然后合并同类项即可.
讲解七:
因式分解
知识复习
一、因式分解的定义
把一个多项式化成几个整式的积的形式
知识复习
二、提取公因式
如果一个多项式的各项都有公因式,可以把该公因式提出来,将多项式分解成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提取公因式.
知识复习
二、提取公因式
2.提公因式后,多项式的项数与原多项式的项数相同;当原多项式的某项与公因式相同时,提公因式后,所得对应项为1
知识复习
二、提取公因式
①定系数:取各项系数的最大公因数
②定字母:取各项相同的字母(多项式)
③定次数:取各项相同字母(多项式)的最低次数
④写公因式:
知识复习
二、提取公因式
① 确定公因式
②把多项式的各项写成含公因式的乘积的形式
③把公因式提到括号外面,余下各项写在括号里面
知识复习
三、公式法:利用乘法公式进行因式分解的方法
平方差公式 完全平方公式
字母表示
语言描述 两个数的平方差,等于这两个数的和与这两个数的差的积 两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方
知识复习
四、延伸:十字相乘
类别 举例
①竖分二次项与常数项
②交叉相乘,积相加 ③检验确定,横写因式 当常数项是正数时,分解的两个因数同号;当常数项是负数时,分解的两个因数异号.
2
命题形式9 提公因式法分解因式
【题型解读】
本题考查代数式求值.先提公因式将代数式进行因式分解,然后将条件代入即可求值.
命题形式9 提公因式法分解因式
【题型解读】
本题考查了提公因式法因式分解,先提公因式a是解题的关键.
命题形式10 公式法分解因式
【题型解读】
本题考查了分解因式,利用完全平方公式分解即可,熟练掌握完全平方公式是解此题的关键.
命题形式10 公式法分解因式
D
命题形式11 综合提公因式和公式法分解因式
【题型解读】
本题考查因式分解,代数式求值,综合提公因式和完全平方公式将多项式进行因式分解,利用整体代入法,求值即可.
我们下节课再见
See you in the next video
专题二 代数式与整式
中考数学一轮复习备考合集
考情分析
命题点 命题形式 命题热度 命题特点
代数式 1.列代数式 ☆ 本专题多以选择题和填空题的形式出现,重点考查学生通过运算法则、运算公式求得运算结果的能力,体现了数学运算的核心素养
2.代数式求值 ☆☆ 整式及其运算 3.整式的加减 ☆☆ 4.幂的运算 ☆☆☆ 5.整式的混合运算 ☆☆☆☆ 因式分解 6.因式分解 ☆☆☆☆
讲解一:
代数式及其分类
知识复习
一、用字母表示数
1.用字母或含有字母的式子表示数或数量关系.在用字母表示数中,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
知识复习
一、用字母表示数
2.用含有字母的式子表示数的书写规定
(2)数与字母相乘时,通常把数写在前面;
(4)带分数与字母相乘时要将带分数化为假分数;
(5)除法运算要表示成分数;
(6)若式子后面有单位且式子是和或差的形式,式子应用小括号括起来.
知识复习
一、用字母表示数
【注意】
1.同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示;
2.用字母可以表示任意数或式子.用字母表示数后,同一式子可以表示不同的含义;
3.用字母表示实际问题中的某个量时,字母的取值必须使式子有意义且符合实际情况.
知识复习
二、代数式的定义
1.单独的一个数或一个字母也是代数式.
用基本运算符号把数和表示数的字母连接起来的式子.
【注意】
知识复习
三、列代数式的要点
通过题目中的关键词(如和、差、积、商、大、小、几倍、几分之几等),找到正确的数量关系.常见数量关系如下:
知识复习
四、代数式求值的常用方法
1.直接代入法:已知字母的值或字母的值可计算时,直接代入求解.
2.整体代入法:字母的值不能或不必计算时,先对已知或所求代数式进行变形(常用到提取公因式、平方差公式、完全平方公式等),再整体代入求解.
命题形式1 列代数式
B
命题形式2 代数式求值
11
命题形式2代数式求值
4
讲解二:
整式的相关概念
知识复习
一、单项式:
类别 定义 示例
系数 单项式中的数字因数
次数 单项式中的所有字母的指数和 单项式的相关概念如下:
知识复习
一、单项式:
1.乘积:只含乘法,不含加法
2.单独的一个数或字母也是单项式
3.分母中不能含有字母
4.若单项式只含有字母因数,则它的系数就是1或-1
5.对于单独一个非零的数,规定它的次数为0
6.π是常数而不是字母
知识复习
二、多项式
类别 定义 示例
项 组成多项式的每个单项式
项数 组成多项式的单项式的个数 次数 多项式中次数最高项的次数 多项式的相关概念如下:
知识复习
多项式
1.不含字母的项叫做常数项
2.多项式的每一项都包括它前面的符号
4.单项式与多项式统称为整式
命题形式3 单项式的有关内容
3
4
命题形式3 单项式的有关内容
【题型解读】
此题考查单项式有关概念,根据单项式次数的定义来求解,解题的关键是需灵活掌握单项式的系数和次数的定义,单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
命题形式4 多项式的有关内容
五
四
讲解三:
整式的加减
知识复习
一、合并同类项
1.同类项:所含字母相同,且相同字母的指数也相同的项
2.同类项与单项式的系数无关,与字母的顺序无关.
3.常数项都是同类项
4.若多个同类项的系数相加为0,则合并后该项为0
将同类项的系数相加,字母与其指数不变
知识复习
二、去括号法则
符号 法则 举例
括号前是 “+” 去、添括号不变号
括号前是“-” 去、添括号都变号
添括号与去括号的过程相反,添括号是否正确,可用去括号检验.
知识复习
三、整式的加减
整式的加减的实质是合并同类项,如果有括号要先去括号,再合并同类项.
命题形式5 整式的加减
A
【题型解读】
本题主要考查合并同类项,根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变即可得.
命题形式5 整式的加减
讲解四:
幂的运算
知识复习
幂的运算
类别 运算法则 运算公式 逆用
同底数幂的乘法
幂的乘方
积的乘方
底数不变,指数相加
底数不变,指数相乘
把积的每一个因式分别乘方,再把所得的幂相乘
知识复习
类别 运算法则 运算公式 逆用
同底数幂的除法
零次幂
负指数幂
底数不变,指数相减
任何非零数的0次幂都等于1
指数转正,再取倒数
幂的运算
命题形式6 幂的运算
D
命题形式6 幂的运算
B
命题形式6 幂的运算
【题型解读】
该题型考查合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键.根据合并同类项法则;同底数幂相乘,底数不变,指数相加;幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减,对各选项分析判断后利用排除法求解.
讲解五:
整式的乘除
知识复习
一、整式的乘法
类别 运算法则 示例
单项式×单项式
单项式×多项式
多项式×多项式
①系数相乘;
②同底数幂相乘;
③单独含有的字母连同指数不变
①单项式乘多项式的每一项;
②积相加
①将多项式的每一项分别相乘
②积相加
知识复习
二、整式的除法
类别 运算法则 举例
单项式÷单项式
多项式÷单项式
①系数相除;
②同底数幂相除;
③只在被除式里含有的字母连同指数不变
①用多项式的每一项除以单项式
②商相加
D
命题形式7 整式的混合运算
【题型解读】
本题主要考查了整式的混合运算,先计算单项式乘以多项式,再合并同类项即可.
C
命题形式7 整式的混合运算
命题形式7 整式的混合运算
【题型解读】
本题考查了合并同类项,积的乘方,单项式除以单项式,单项式乘以单项式,根据合并同类项,积的乘方,单项式除以单项式,单项式乘以单项式法则逐项排除即可,熟练掌握运算法则是解题的关键.
命题形式7 整式的混合运算
讲解六:
乘法公式
知识复习
一、平方差公式:
知识复习
一、平方差公式:
1.位置:
2.系数:
3.指数:
4.项数:
知识复习
二、完全平方公式:
完全平方公式 和的完全平方公式
差的完全平方公式
知识复习
三、【难点突破】
在用完全平方公式对代数式变形时,常用到下列关系:
命题形式8 利用乘法公式解题
命题形式8 利用乘法公式解题
【题型解读】
根据单项式乘以多项式和完全平方公式法则分别计算,然后合并同类项即可.
讲解七:
因式分解
知识复习
一、因式分解的定义
把一个多项式化成几个整式的积的形式
知识复习
二、提取公因式
如果一个多项式的各项都有公因式,可以把该公因式提出来,将多项式分解成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提取公因式.
知识复习
二、提取公因式
2.提公因式后,多项式的项数与原多项式的项数相同;当原多项式的某项与公因式相同时,提公因式后,所得对应项为1
知识复习
二、提取公因式
①定系数:取各项系数的最大公因数
②定字母:取各项相同的字母(多项式)
③定次数:取各项相同字母(多项式)的最低次数
④写公因式:
知识复习
二、提取公因式
① 确定公因式
②把多项式的各项写成含公因式的乘积的形式
③把公因式提到括号外面,余下各项写在括号里面
知识复习
三、公式法:利用乘法公式进行因式分解的方法
平方差公式 完全平方公式
字母表示
语言描述 两个数的平方差,等于这两个数的和与这两个数的差的积 两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方
知识复习
四、延伸:十字相乘
类别 举例
①竖分二次项与常数项
②交叉相乘,积相加 ③检验确定,横写因式 当常数项是正数时,分解的两个因数同号;当常数项是负数时,分解的两个因数异号.
2
命题形式9 提公因式法分解因式
【题型解读】
本题考查代数式求值.先提公因式将代数式进行因式分解,然后将条件代入即可求值.
命题形式9 提公因式法分解因式
【题型解读】
本题考查了提公因式法因式分解,先提公因式a是解题的关键.
命题形式10 公式法分解因式
【题型解读】
本题考查了分解因式,利用完全平方公式分解即可,熟练掌握完全平方公式是解此题的关键.
命题形式10 公式法分解因式
D
命题形式11 综合提公因式和公式法分解因式
【题型解读】
本题考查因式分解,代数式求值,综合提公因式和完全平方公式将多项式进行因式分解,利用整体代入法,求值即可.
我们下节课再见
See you in the next video
同课章节目录
